混凝土空心板梁橋地震損傷指標分析
吳建臻
(福建農業職業技術學院,福建 福州 350002)
0 引言
由于橋梁結構在交通生命線系統中不可替代的重要作用,它的抗震能力是影響整個系統防災能力的關鍵要素之一。為了將橋梁結構的地震損傷控制在一定的范圍內,必須對橋梁結構先進行損傷分析。迄今為止,國內外現行的許多抗震設計規范和標準中提供了許多橋梁結構破壞或失效的判別準則,但是,例如損傷程度的量化,中等損傷和嚴重損傷判別的界限值,現行的規范或標準中卻沒有提及[1-2]。為了客觀評價橋梁結構在各等級地震動作用下的損傷程度,應當將橋梁結構的損傷程度和地震反應的峰值聯系在一起,確定橋梁結構各級損傷狀態的指標,并對其進行量化,定義各級破壞狀態的界限值[3]。
1 空心板梁橋的地震損傷
橋梁結構主要由上部結構、下部結構和支承連接裝置組成。由于橋梁上部結構一般都采用彈性設計理論設計,所以從強度上說十分的堅固,在地震作用下主梁本身基本處于彈性階段,它的震害主要是由支承連接裝置或下部結構的破壞引起的,因此,橋梁系統中最易發生損傷情況的主要有下面3種:橋梁墩柱的損傷、支承與連接裝置的損傷、蓋梁以及基礎的損傷。對混凝土空心板梁橋來說,墩柱應該設置為延性構件,橋梁的上部結構、其他的下部結構均應設置為能力保護構件。
另外,板式橡膠支座作為混凝土空心板梁橋中最常用的支承類型,具有傳遞上部結構反力以及承受水平向位移的作用,而且具有一定的減震隔震性能。在地震作用下,板式橡膠支座能夠在一定程度上延長結構的周期,并且增強結構的阻尼,達到減少橋墩的地震反應需求的效果。但是橡膠支座降低橋梁部分構件地震作用下內力需求是以其本身的位移反應增大為代價的。所以梁式橋采用板式橡膠支座時,橡膠支座的變形承擔了相當一部分的地震作用,所以支座的位移反應成了判斷橋梁地震損傷的主要根據。
2 空心板梁橋結構的損傷指標
損傷指標是用來標定結構或構件在給定作用下損傷程度的數學表達式。橋梁結構的損傷指標又可以分為各構件的損傷指標和橋梁結構整體的損傷指標2個方面。由于橋梁各個構件在設計上的控制參數有很大的不同,因此很難建立橋梁整體的損傷指標。所以,目前應用比較廣泛的損傷指標是構件的損傷指標。而想要建立構件的損傷指標,就需要解決2個方面的問題:1)確定損傷指標的表達式;2)界定各級損傷的界限值,也就是明確各級損傷程度的數值區間。
2.1 橋墩墩柱的損傷指標
鋼筋混凝土橋墩主要有2種破壞類型:1)由于彎曲強度不足而引起的墩柱的輕微開裂、保護層混凝土的剝落以及縱向鋼筋的屈曲和斷裂等;2)由于設計彎曲延性不足或者塑性鉸區域設計抗剪強度不足而造成的彎剪破壞或剪切破壞。
2.1.1 墩柱彎曲破壞的損傷指標
橋梁墩柱的彎曲破壞屬于延性破壞,目前的抗震設計理論普遍認為,鋼筋混凝土墩柱在比較強烈的地面運動的作用下,會在墩柱的底部或者端部區域形成塑性鉸,而塑性鉸也正是損傷集中發生的部位[4]。所以,用延性來定義橋梁墩柱彎曲破壞的指標是比較恰當的。延性,定義為給定變形與屈服時變形的比值,筆者稱之為延性系數。目前,被應用作為損傷指標的延性系數主要是位移延性系數μΔ和曲率延性系數μφ,見式(1) 、式(2)。

式中:Δ,φ分別是構件在給定變形狀態下的柱端位移和截面曲率;Δy,φy則為2個參數在構件理論屈服點上的數值。
Hose[5]等(1999)的模型試驗研究結果顯示:塑性鉸形成、發展和失效的過程,也正對應著橋梁墩柱的中等損傷、嚴重損傷和完全損傷,所以墩柱塑性鉸截面的首次屈服、等效屈服和極限屈服點,可以定義為各級破壞狀態的界限值,整理可得到橋墩墩柱彎曲破壞的損傷指標,見表1。
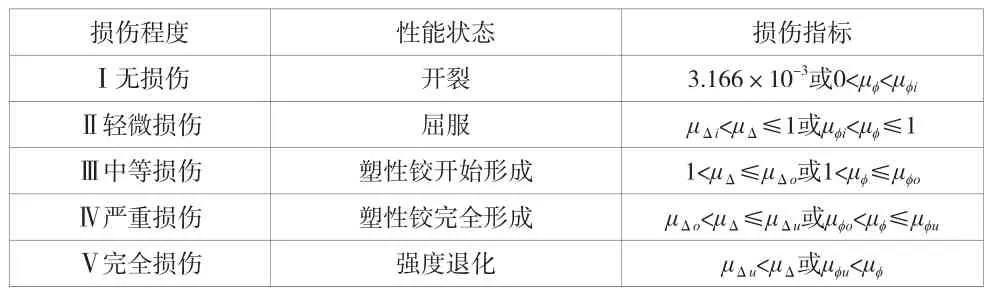
表1 墩柱彎曲破壞的損傷指標
在這里,偏保守的取μΔ=1作為輕微損傷與中等損傷的臨界點,主要考慮以下3個方面:1)在橋梁的抗震設計理論中,μΔ=1是構件進入塑性變形的起始點。2)在橋梁抗震設計與加固中,由于輕微損傷和中等損傷的可修復性,所以它們的臨界點在工程界所受的關注程度遠遠小于不可修復性的損傷。3)采用μΔ=1作為輕微損傷和中等損傷位移延性的臨界值,物理意義清晰明確,便于實際應用。
2.1.2 考慮墩柱剪切破壞的損傷指標
剪切破壞是抗震設計力圖避免的一種破壞形式。但是,就目前的很多混凝土空心板梁橋來說,由于建設的年代比較早,很多采用了較落后的抗震設計規范,所以并沒有按照能力保護原則進行設計驗算,同時混凝土空心板梁橋的橋墩以矮墩居多,墩柱的配箍率較低,許多橋梁墩柱的抗剪能力嚴重不足,導致地震作用下,很多橋梁的墩柱很容易產生彎剪破壞,甚至是脆性剪切破壞[6]。
參考美國公路橋梁抗震加固手冊(1995),評估橋墩是否發生剪切破壞的標準如圖1所示。只有滿足式(3)時,才可以判斷橋墩不會發生剪切破壞。
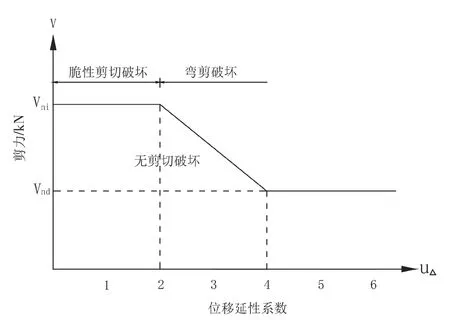
圖1 墩柱剪切破壞的判別標準

式中:Vn為名義抗剪能力(單位:kN);Vo為超強彎矩對應的剪力,是墩柱可能承受的最大剪力(單位:kN)。
要對鋼筋混凝土墩柱進行抗剪能力驗算時,必須先計算出墩柱可能承受的最大剪力作為設計剪力,然后再進行抗剪驗算。根據最新的公路橋梁抗震設計規范,墩柱順橋向和橫橋向剪力設計值Vco應該根據可能出現塑性鉸處按照實配鋼筋,采用材料標準強度值和軸壓力計算出彎矩承載能力,考慮超強系數系數φ°來計算。
對混凝土空心板梁橋,其橋墩多為多柱式橋墩,沿順橋向,鋼筋混凝土橋墩的底部區域為潛在塑性鉸區域,對墩底截面進行M-φ分析和P-Δ分析,根據相關規范的規定,可以得到墩柱截面在達到等效屈服彎矩和極限屈服彎矩時的抗剪需求,如公式(4)和公式(5)所示。


式中:Vdi為塑性鉸截面達到等效屈服時的抗剪需求;Vdu為塑性鉸截面達到極限屈服時的抗剪需求;φ°為橋墩正截面抗彎承載能力超強系數,φ°=1.2;Py為塑性鉸截面等效屈服時的最不利軸力;Pu為塑性鉸截面極限屈服時的最不利軸力;My為屈服彎矩;Mu為極限彎矩;Hn一般為墩柱凈長度,但是對單柱墩橫橋向計算時應取梁體截面形心到墩柱底截面的垂直距離。
而沿橫橋向,鋼筋混凝土橋墩墩柱的頂、底部區域在地震作用下都會產生塑性鉸。由于蓋梁的約束作用,多柱式橋墩在橫橋向地震作用下會產生軸力,所以此時,墩柱的軸力其實是由重力和地震產生的軸力共同確定的。由于地震軸力是動態的,只有通過實驗才能確定,所以,該文在分析時僅考慮重力作用下產生的軸力。在重力軸力作用下,對墩頂和墩底截面進行M-φ分析和P-Δ分析,得到分析參數。如果忽略橋墩自身的重力,那么墩頂和墩底截面的分析參數可以認為是一致的,可以偏安全地取墩底截面的分析參數,那么就可以得到墩柱截面在橫橋向地震作用下達到等效屈服彎矩和極限屈服彎矩時的抗剪需求,如公式(6)和公式(7)所示。

當Vni>Vdi,且Vnd>Vdu時,橋墩墩柱會發生彎剪破壞。此時,偏安全的在抗剪能力曲線上取Vn>Vdu所對應的μΔ值作為橋墩完全損傷的起點,即認為從這一點開始,橋墩發生彎剪破壞,如圖2所示。所以,橋墩墩柱彎剪破壞的損傷指標見表2。
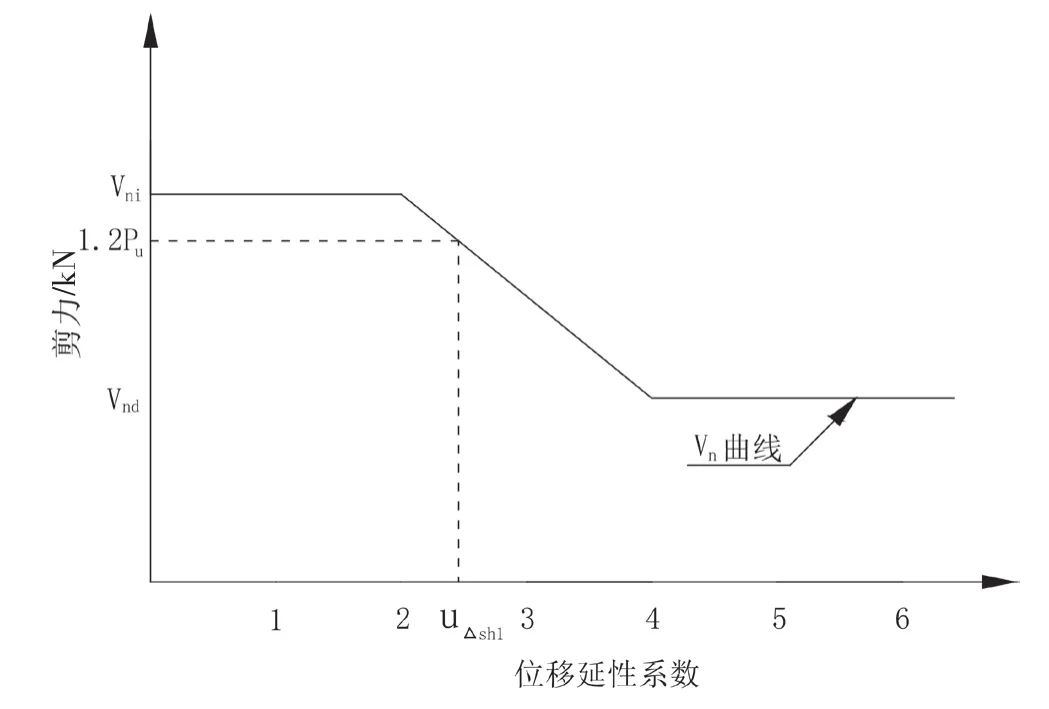
圖2 彎剪破壞的V-μΔ曲線
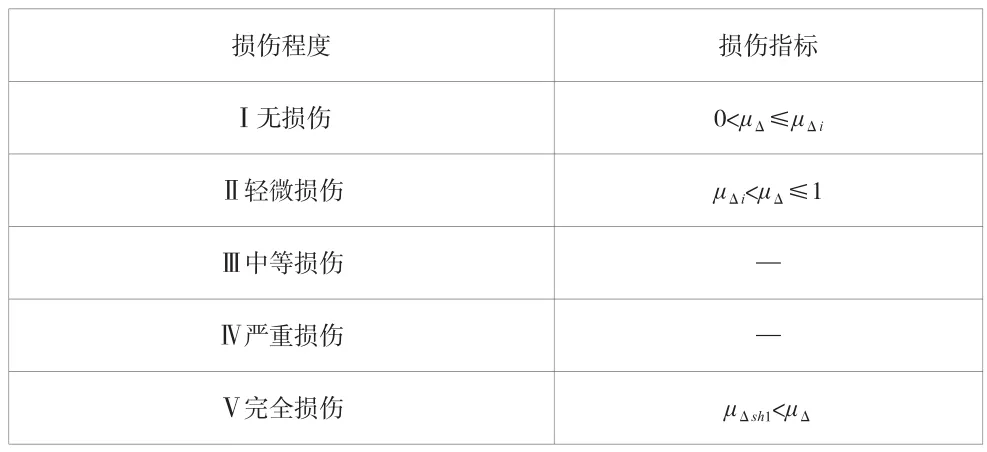
表2 墩柱彎剪破壞的損傷指標
當Vni<Vdi,且Vnd<Vdu時,墩柱將發生脆性剪切破壞。此時,只要在地震作用下,墩柱危險截面的剪應力V>Vni,墩柱馬上發生脆性剪切破壞,但是為了使墩柱彎曲破壞和彎剪破壞一致,筆者希望用位移延性比來定義墩柱剪切破壞的準則。因為墩柱在等效屈服時的抗剪需求為Vdi,對應的位移是Δy,那么按比例關系,當地震反應V>Vni所對應的柱端位移如公式(8)所示。

相應的位移延性系數如公式(9)所示。

式中:Δsh2為墩柱危險截面的剪應力等于初始剪切強度Vni時的柱端位移;μΔsh2為墩柱危險截面的剪應力等于初始剪切強度Vni時所對應的位移延性系數。
因為Vni<Vdi,所以在數值上μΔsh2<1。墩柱發生剪切破壞又可以分為2種情況,一是在墩柱危險截面的鋼筋首次屈服前,墩柱發生脆性剪切;二是墩柱危險截面的鋼筋首次屈服后,墩柱發生剪切破壞。這2種情況對應的損傷指標見表3。

表3 墩柱脆性剪切破壞的損傷指標
2.2 板式橡膠支座的損傷指標
板板式橡膠支座,因其具有簡單的構造特性,以及合理的受力性能,所以廣泛應用于中小跨徑的梁式橋中。其剪力—位移滯回曲線呈狹長型,近似處理時可以認為是線性的,如圖3所示。
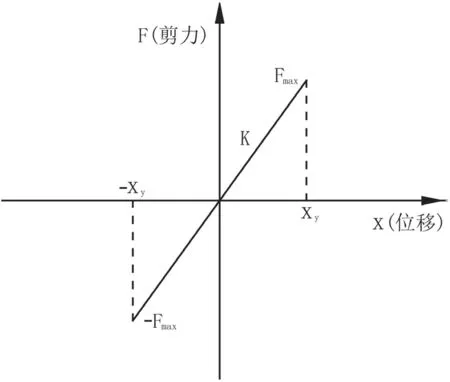
圖3 板式橡膠支座線性模型
而板式橡膠支座作為彈性支座,在地震作用下的破壞形式多為剪切破壞[7]。該文采用相對位移延性比來定義板式橡膠支座的4種損傷指標,而支座相對位移延性比如公式(10)所示。

式中:Δz為地震作用下支座最大相對位移,Δ1為支座剪切應變等于100%時的相對位移。根據最新的公路橋梁抗震規范的相關規定,取支座剪切應變等于100%、150%、250%時的相對位移延性比為各級損傷狀態的界限值。所以,支座損傷指標與各級損傷狀態之間的關系見表4。
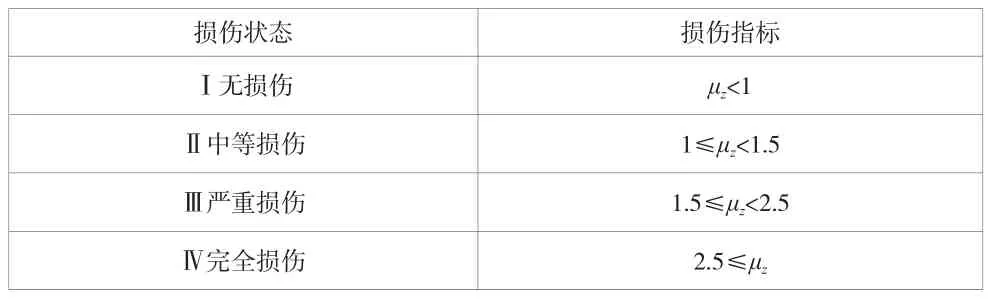
表4 板式橡膠支座損傷指標
3 結論
該文對混凝土空心板梁橋進行了地震易損性損傷分析,得到以下結論:1)針對現有混凝土空心板梁橋性能水平,分析并確定了其在地震作用下最易發生損傷的構件:橋墩墩柱以及支承和連接裝置。2)針對橋墩墩柱在地震作用下可能發生的2種破壞狀態:彎曲破壞和剪切破壞,統一采用位移延性系數作為橋墩墩柱損傷的控制參數,定義了橋墩墩柱在不同破壞形式下的損傷指標。3)針對混凝土空心板梁橋中最常用的支承連接裝置板式橡膠支座的受力特性,以及抗震規范中關于橡膠支座在不同等級的地震作用下的容許剪切應變值的規定,以相對位移延性比為控制參數,確定了板式橡膠支座的損傷指標。

