不規則樓板有限元計算與分析

蔣文 姜早龍

湖南湖大建設監理有限公司 湖南 長沙 410013

引言：隨著社會經濟水平的持續提升，人民群眾對建筑居住環境的訴求也在不斷產生新的變化。這些新的市場需求變化，給工程結構設計帶來新的機遇和挑戰。在住宅工程中，客廳和餐廳交界位置一般均布置結構梁，將樓板分割形成規則矩形樓板，再采用成熟的單雙向矩形樓板設計方法進行結構設計。在某實際工程中，建筑師要求取消交界位置的結構梁，以達到室內天花無明梁的美觀效果，提高建筑居住品質。由于不規則樓板的形狀較為特殊、受力更為復雜，直接套用單雙向矩形樓板設計方法的做法將可能使該類樓板結構存在安全隱患。因此，明確不規則樓板的受力特征和設計要點，具有十分重要的工程意義。

1 不規則樓板結構計算

1.1 樓板結構布置

某實際工程為17層高層住宅，結構類型為剪力墻結構。應建筑師對室內空間美觀實用的要求，標準層結構設計時不可避免地產生了兩類不規則樓板LB1和LB2，詳細尺寸如圖1所示。樓板厚度h=130 mm，混凝土強度等級為C30，恒荷載標準值[1]（包括板自重）gk=1.5 kN/m2+0.13 m×27 kN/m3=5.0 kN/m2，活荷載標準值qk=2.0 kN/m2。

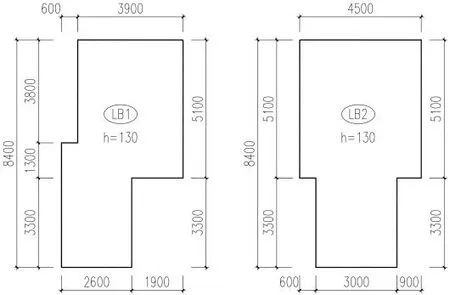
圖1 不規則樓板LB1、LB2詳細尺寸(mm)

結構標準層中，不規則樓板與周邊樓板形成連續板帶，因此在計算中，樓板各邊界條件均按固結考慮。

1.2 PKPM樓板內力計算

PKPM軟件可以根據結構板的類型，自動選擇與其所對應適用的的計算方法[2-4]。當識別為凸形不規則板時，采用邊界元法進行計算；識別為凹形不規則板時，則采用有限元方法進行計算。

對于與規則矩形樓板較接近，但局部存在異形的樓板，比如，規則房間局部缺角，某個角不是直角或某個板邊為弧形，尤其是當不規則的程度較小時，其板的內力計算結果與規則板的計算結果基本接近，PMCAD提供了一個參數供工程師定義：近似按矩形計算時面積相對誤差，默認值為0.15。通過修改該參數數值，工程師可以靈活調整軟件對不規則樓板的包容度。當實際相對誤差值大于自定義相對誤差值，程序將按不規則樓板進行計算。

不規則樓板LB1和LB2實際相對誤差分別為：εLB1=1-(2.6×3.3+1.3×4.5+3.9×3.8)/(4.5×8.4)=1-0.77=0.23，εLB2=1-(3×3.3+4.5×5.1)/(4.5×8.4)=1-0.87=0.13。本實際工程中，定義相對誤差參數值為0.10，小于實際相對誤差較小值0.13，軟件將按不規則樓板類型進行結構計算。不規則樓板LB1和LB2的彎矩計算值，如圖2所示。

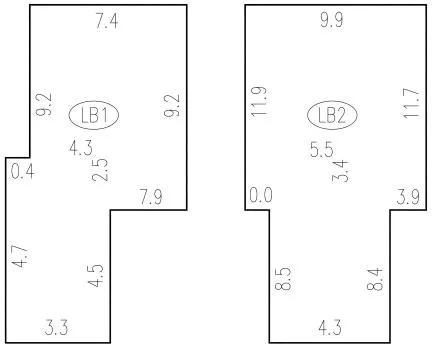
圖2 不規則樓板LB1、LB2彎矩計算值(kN·m)

2 不規則樓板有限元計算分析

為準確掌握不規則樓板的受力特征，在建筑結構通用有限元分析軟件midas Gen中分別建立LB1、LB2的有限元計算模型。有限元網格單元劃分尺寸取為0.3m，指定樓板區域自動劃分網格，并進行有限元求解[5]。

2.1 midas Gen樓板有限元計算

不規則樓板LB1有限元計算結果如圖3、圖4所示。

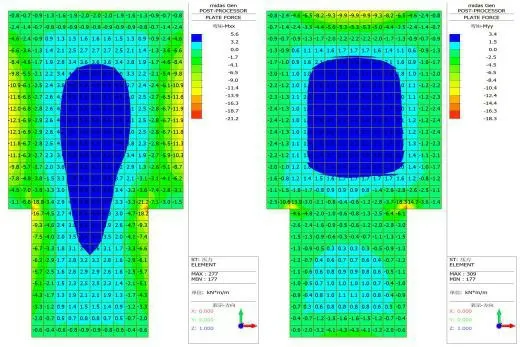
圖3 不規則樓板LB1沿X向、Y向單位寬度彎矩圖(kN·m/m)

圖4 不規則樓板LB1沿Z向變形圖(mm)

不規則樓板LB1板底最大單位寬度彎矩為X=4.4 kN·m/m，Y=2.5 kN·m/m，位于上部板塊跨中，板底同位置X向彎矩大于Y向彎矩；板面支座最大單位寬度彎矩為-9.4 kN·m/m，位于邊界6；在兩個凸角位置，均存在應力集中現象，應力集中主要分布在以凸角為圓心，半徑為兩個單位尺寸，即600mm左右的區域內。

邊界7以上的上部板塊、邊界3以下的下部板塊其內力分布規律與普通雙向板基本相同，上部板塊在類似位置其內力均大于下部板塊，連接上下板塊的中部板塊受力最為復雜。

不規則樓板LB1沿Z向變形最大值為0.7mm，出現在上部板塊跨中位置，變形等值線以最大值點為中心，由橢圓形逐漸擴展為LB1樓板的形狀。

不規則樓板LB2有限元計算結果如圖5、圖6所示。

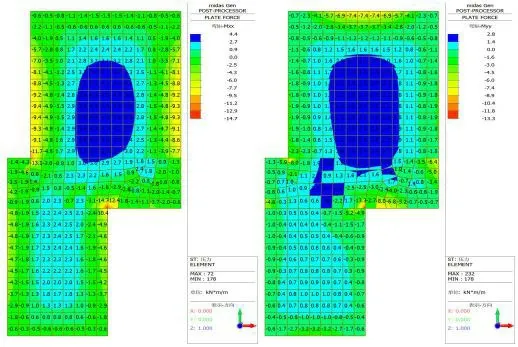
圖5 不規則樓板LB2沿X向、Y向單位寬度彎矩圖(kN·m/m)

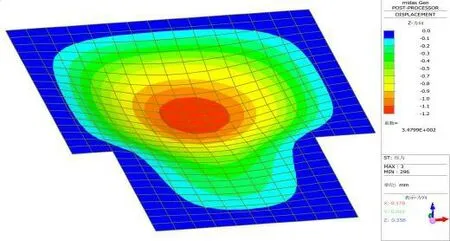
圖6 不規則樓板LB2沿Z向變形圖(mm)

不規則樓板LB2板底最大單位寬度彎矩為X=5.6 kN·m/m，Y=3.4 kN·m/m，位于整塊板中部偏上位置，板底同位置X向彎矩大于Y向彎矩；板面支座最大單位寬度彎矩為-12.1 kN·m/m，位于邊界6；在兩個凸角位置，均存在應力集中現象，應力集中主要分布在以凸角為圓心，半徑為1個單位尺寸，即300mm左右的區域內。

上部板塊其內力分布規律與普通雙向板基本相同。下部板塊X向彎矩從下往上不斷變大，Y向彎矩在跨中為正值，在兩板塊邊界線上下為負值，中部負彎矩分別向左右支座變大。

不規則樓板LB2沿Z向變形最大值為1.2mm，出現在上部板塊跨中位置，變形等值線以最大值點為中心，由橢圓形逐漸擴展為LB2樓板的形狀。

綜上所述，不規則樓板在內力分布、變形特征上與規則矩形樓板存在顯著差異，內部凸角位置存在應力集中現象。建議在工程設計中采用有限元方法，對不規則程度較大的樓板進行專項分析和設計，正確得到其在豎向荷載作用下的內力分布及其變形特征，并針對性地提出加強措施。

2.2 兩種軟件計算結果對比分析

提取PKPM與midas Gen有限元計算結果進行對比，如表1：

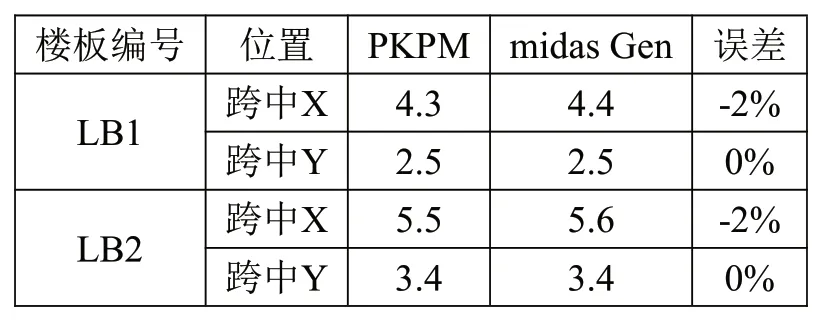
表1 計算結果對比

跨中彎矩最大誤差為-2%，PKPM與midas Gen計算結果基本一致。支座彎矩存在不同程度的差異，局部位置差異較大。工程設計中，建議采用有限元軟件對不規則樓板結構計算結果進行復核。

3 結論

1）工程師應當謹慎定義PMCAD中參數：近似按矩形計算時面積相對誤差，否則不規則樓板按照規則樓板計算，會導致不正確的內力計算結果。

2）通過合理調整PKPM軟件的計算參數，其跨中彎矩的計算結果可用于工程設計，但支座彎矩計算結果存在一定誤差，局部位置誤差較大，建議采用有限元軟件進行復核。

3）與規則樓板相比，不規則樓板在豎向荷載作用下的內力分布和變形特征更為復雜多變，建議在工程設計中采用有限元方法，對不規則程度較大的樓板進行專項分析和設計。