考慮風險等級的車車通信MTTC混合分布模型

王江鋒，熊慧媛，徐 亮，閆學東，郭魁元

(1. 綜合交通運輸大數據應用技術交通運輸行業重點實驗室(北京交通大學)，北京 100044;2.中國汽車技術研究中心有限公司，天津 300300)

中國近期發布的《交通強國建設綱要》要求“提升本質安全水平”[1]。雖然中國交通運輸安全整體形勢已得到了改善，但重特大交通事故時有發生，這就為中國車輛運行安全評估提出了更高要求。伴隨著智能網聯交通的快速發展，諸如車車通信等一些新技術將會對異質混合交通流的運行規律產生重要影響，使其蘊含的車輛運行風險更加復雜，并可能出現一些未知的道路交通風險。因此，有必要對車車通信環境下的車輛運行安全指標進行研究，以提高智能網聯環境下的車輛運行安全[2-3]。

既有研究針對常規車輛和網聯車輛在混合交通流下車輛運行安全進行了探討。一方面，已有研究基于數值仿真數據或一般交通流數據進行研究。例如，文獻[4]利用數值仿真，選取多項安全評價指標對異質混合交通流下車輛運行安全進行評估，結果表明智能網聯車能夠有效地提高車輛運行安全；文獻[5]通過數值仿真，在不同CAV滲透率條件下，分析了CAV混合交通流的優化控制法對車輛追尾碰撞風險的影響，結果表明采用該方法可降低車輛追尾碰撞風險；文獻[6]提出網聯環境下基于安全勢場理論的車輛跟馳模型，用于描述考慮加速度參數條件下的跟馳行為，并用NGSIM數據標定模型參數，建立的基于安全勢場理論的車輛跟馳模型具有良好的精度。另一方面，由于傳統的車輛運行安全評估方法大多依賴于歷史事故數據，該類方法存在數據收集時間長、事故記錄漏報以及事故記錄不準確等諸多局限性[7]，相應地，間接安全評價方法(surrogate safety measures，SSMs)隨之而生。SSMs是一種基于交通沖突理論的主動車輛運行安全評估方法，目的在于將識別出的非碰撞事件進一步轉換為相應的危險程度，不依賴歷史碰撞事故數據即可實現對車輛運行安全的評估[8]。目前SSMs方法主要有碰撞時間(time-to-collision，TTC)[9]、后侵占時間(post-encroachment time，PET)[7]、停車距離比例(proportion of stopping distance，PSD)[10]以及避撞減速度(deceleration rate to avoid collision，DRAC)[11]。上述SSMs未同時考慮前后車相對速度及相對加速度。因此，文獻[12]基于牛頓運動方程提出MTTC(modified time-to-collision)并確立了其滿足的關系等式，并在仿真環境下驗證了MTTC能以較高的置信度捕獲實際路況下的車輛運行安全特性。

已有研究多基于微觀仿真數據或一般環境下實驗數據進行研究，鮮有文獻以車車通信環境的車輛行駛實測數據為基礎進行MTTC混合分布模型研究。此外，已有研究忽略了車輛運行風險等級的差異性對MTTC分布的影響，然而不同風險等級的差異性是影響車輛運行安全的重要因素[13]。因此，本文針對不同車輛運行風險等級，基于車車通信環境下實測數據對MTTC混合分布模型進行研究，并利用一般環境下實測數據對該模型的適應性進行分析。

1 MTTC概念

鑒于加速度反映了車輛行駛狀態趨勢，Ozbay等[12]基于牛頓運動學方程定義了MTTC，以預測車輛運行中發生碰撞的可能性。圖1為車輛發生縱向碰撞示意圖。其中，t為當前行駛時刻，t0為初始時刻，d為前后車初始間距。

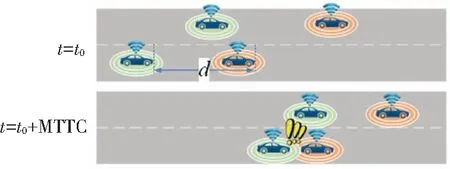
圖1 車輛縱向碰撞示意

在這種情況下，同一車道的前后兩車發生碰撞的條件為

(1)

(2)

式中：vf、vl分別為后車和前車的速度，af、al分別為后車和前車的加速度, Δv=vf-vl，Δa=af-al。

令

(3)

(4)

式中t1、t2表示MTTC的兩種解。

則MTTC的取值可表示為

(5)

式中min(·)表示求最小值。

MTTC的值越小，前后兩車發生追尾碰撞的風險越大。當MTTC>20 s時，駕駛人有充足的時間對突發情況進行反應并采取避讓措施[14]。因此，對小于20 s的MTTC進行統計分析是研究的重點。

2 實驗及數據準備

2.1 實驗條件

為獲取分析MTTC所需的車輛行駛信息，于2019年5月22日在北京交通大學車輛協同實驗場進行了車車通信場地實驗和一般環境場地實驗，實驗道路為3.2 km的雙向兩車道，實車實驗路線如圖2所示，實車實驗場景如圖3所示。為保證實驗安全進行，實驗場地無行人及其他社會車輛出現。

圖2 實車實驗路線

圖3 實車實驗場景

以奇瑞和福特兩品牌的5座轎車為實驗車，分別安裝了OBU設備、LTE-V設備、GPS及各類車載傳感器，車速測量精度為0.01 km/h，加速度測量精度為0.01 m/s2，差分GPS定位精度為1 cm。每輛實驗車上分別有一位駕駛員、一位測量操作員和一位聯絡員。測量操作員坐在實驗車副駕駛位，負責監控設備運行狀態，在出現LTE-V通訊連接中斷或者衛星定位終端信號中斷時，及時進行處理，并通過聯絡員將異常情況告知其他車輛。為保證兩次實驗的外界條件相對一致，車車通信場地實驗和一般環境場地實驗采用相同的實驗車及車載傳感器設備。另外，一般環境場地實驗時，實驗車關閉LTE-V通訊設備，其他設備保持開啟狀態。

2.2 數據獲取

采集的實驗數據包括前后車的差分GPS定位數據、LTE-V設備發送和接收數據、通信延遲數據、事件日志數據等5類信息，主要記錄車輛的位置、行駛狀態以及通信相關參數，所采集的實驗數據見表1，實驗數據的統計特征見表2。

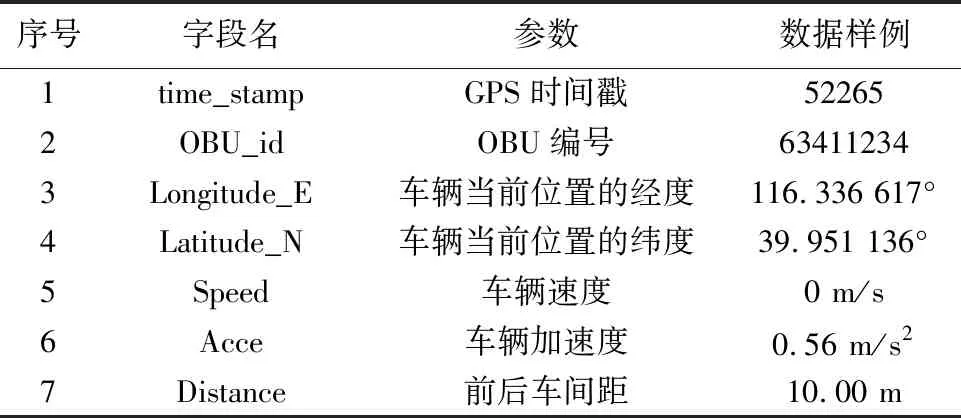
表1 實驗數據類型

表2 實驗數據統計特征

在車車通信場地實驗和一般環境場地實驗獲取的實驗樣本數據中，共選取500條實驗數據作為樣例數據，前后車的速度、加速度變化規律分別如圖4、5所示。

由OBU編號區分前車和后車，由兩車的速度和加速度計算出前后車的相對速度和相對加速度。實驗數據采樣時間間隔為1 s，實驗采集到車車通信環境下實驗數據量為2 800個，一般環境下實驗數據量為1 800個，對數據進行預處理并剔除部分無效數據后，車車通信環境下實驗數據量為2 562個，一般環境下實驗數據量為1 583個，然后篩選出MTTC<20 s的車輛行駛運動學數據后，車車通信環境下實驗數據量為1 888個，一般環境下實驗數據量為1 194個，將篩選后的數據作為實驗樣本進行分析。

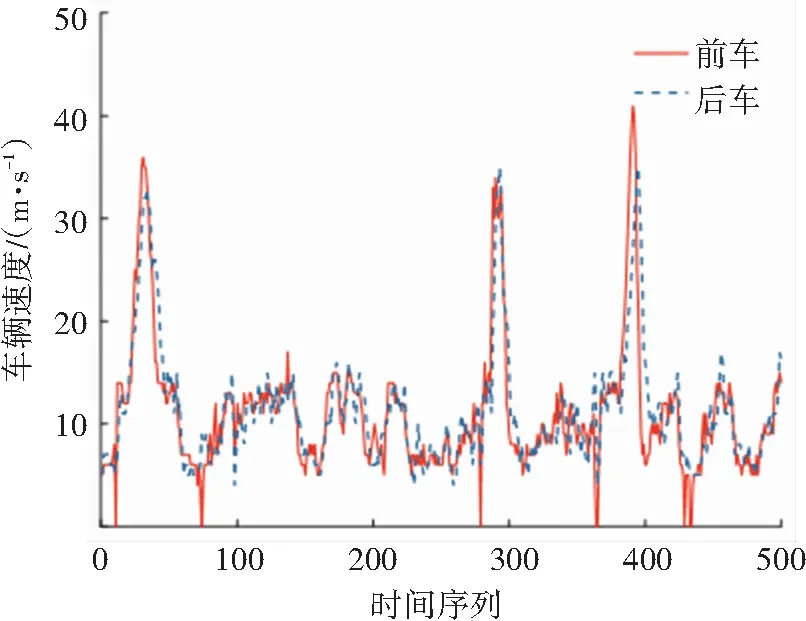
圖4 前后車速度變化規律

圖5 前后車加速度變化規律

3 車輛運行風險等級劃分

為研究車車通信環境下車輛運行風險等級對MTTC分布的影響，需要獲取不同風險等級的車車通信車輛行駛運動學數據。利用表3中MTTC<20 s的車車通信實驗樣本數據，采用文獻[15]提出的駕駛人風格分類類似思路，基于k-means算法對車輛運行風險等級進行劃分。

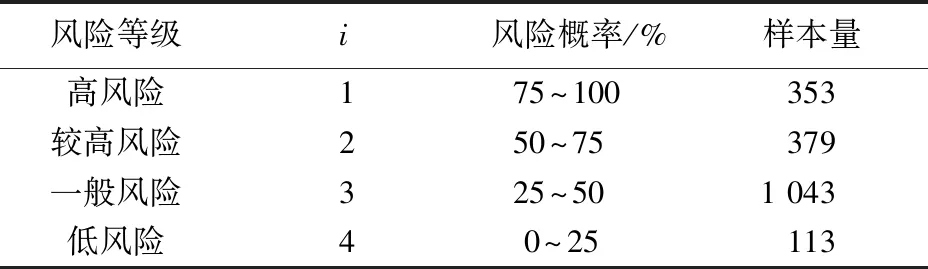
表3 4種風險等級樣本描述

由式(3)～(5)可知，MTTC的計算過程只涉及d、Δv以及Δa，不同風險等級下3個參數具有不同的數值分布，因此，確定上述3個參數作為輸入特征進行聚類分析以獲得不同風險等級的車輛行駛運動學數據，分類流程如圖6所示。

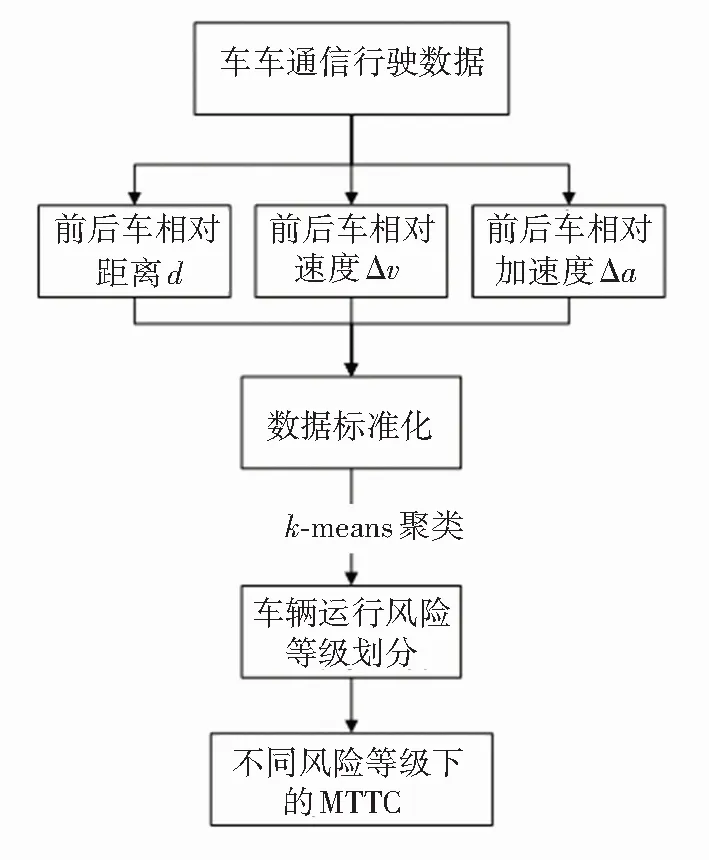
圖6 MTTC數據分類流程圖

3.1 數據標準化

為解決各特征之間數值差異過大的問題，在進行聚類分析前，需對特征數據進行標準化處理。采用min-max標準化方式對原始數據進行線性變換，使特征值都映射到[0,1]內。其轉換函數為

(6)

式中：x為原始數值；max為樣本數據最大值；min為樣本數據最小值；x*為歸一化轉換后的值。

按照式(6)對前后車間距、相對速度以及相對加速度的樣本數據均進行歸一標準化處理，處理后的各特征數據皆在[0,1]內，處于同一個數量級。

3.2 k-means聚類

k-means算法的任務是將數據集劃分成k類，其損失函數通常為誤差平方和函數。定義式為

(7)

式中:k為類別數；Ci為第i類聚集中心域的樣本集合；X為數據對象；μi為第i類的類中心, 類中心為

(8)

其中Ni為Ci中的樣本數。

3.3 風險等級分類結果

依據《國家突發公共事件總體應急預案》[16]分類方法，將風險等級劃分為高、較高、一般、低4個等級。利用k-means聚類方法確定每種風險等級的樣本數據，其中類別數k取4。將車車通信環境下獲取到的前后車的d、Δv、Δa作為輸入特征值，并采用歐幾里得距離函數。3個參數聚類的標準化結果如圖7所示。

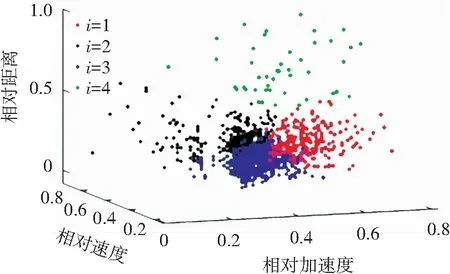
圖7 3個參數聚類標準化結果

由圖7可知，i=1的樣本數據主要集中在前后車間距較小，相對加速度較大的區域；i=2的樣本數據主要落在間距較小，相對速度較大，后車相對前車減速或者加速度較小的區域；i=3的樣本數據聚集在前后車間距較小，相對速度較小，后車相對前車減速或者加速度較小的區域；i=4的樣本數據主要分布在間距較大的區域。借鑒文獻[17]中關于風險等級與車輛運行風險發生概率的對應關系，結合實際車輛運行情景，i=1對應高風險，i=2對應較高風險，i=3對應一般風險，i=4對應低風險，4種風險等級的樣本描述見表3。 由表3可知，車輛在場地實驗過程中大部分時間都處于一般風險及以下，少部分時間處于較高風險及以上。

為驗證不同風險等級下3個參數的分布數值具有差異性，對3個參數分別進行單因素方差分析，方差分析結果見表4。

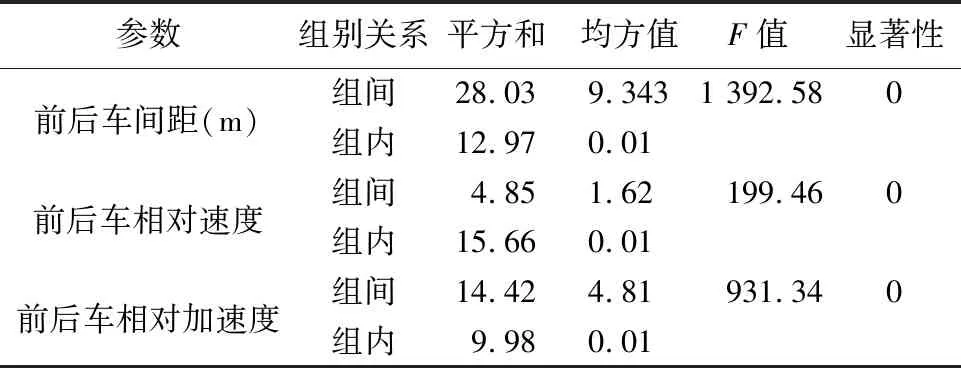
表4 3個參數單因素方差分析結果

由表4可知，相伴概率均小于0.05，表明在0.05的顯著性水平下，4種風險等級的d、Δv和Δa存在顯著差異，從而驗證了不同風險等級下3個參數具有不同的分布數值。

為驗證不同風險等級之間存在差異性，基于LSD(least-significant difference)法對4種風險等級下MTTC進行多重比較分析，多重比較結果見表5，其中，I、J均為組別，代表風險等級。

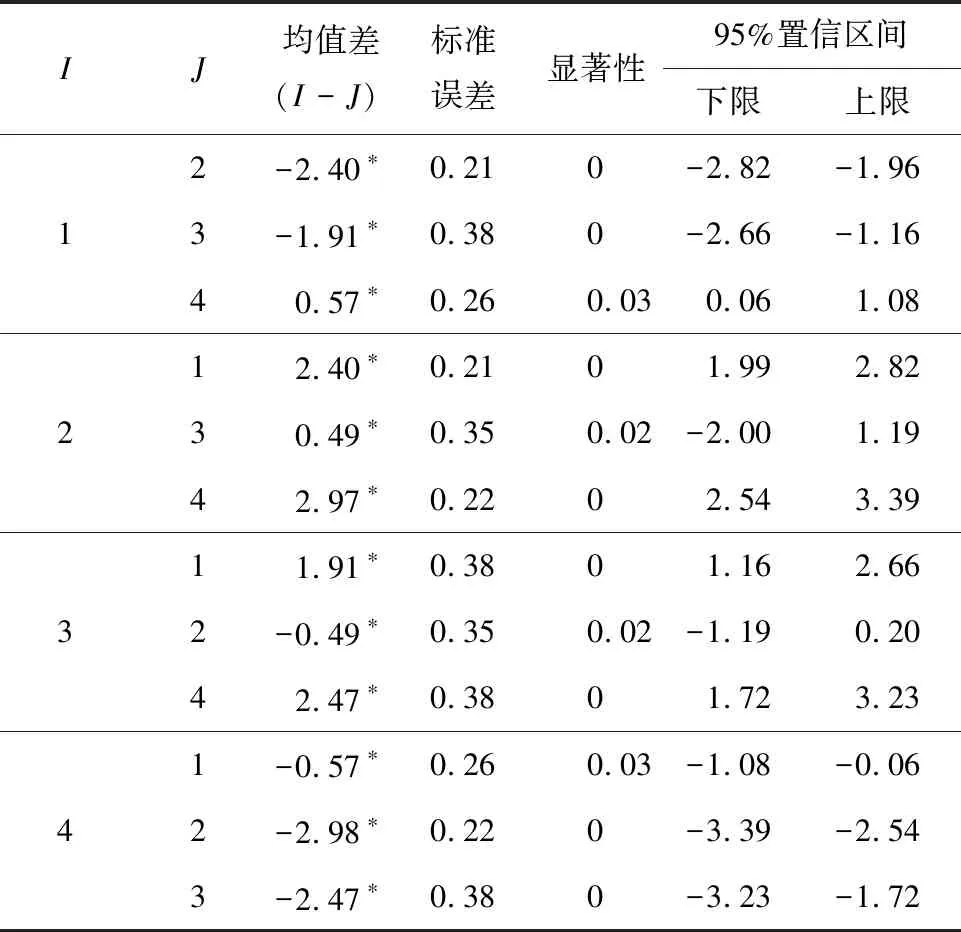
表5 不同風險等級MTTC多重比較結果

由表5可知，4種風險等級之間的相伴概率均小于0.05。說明在0.05的顯著性水平下，4種風險等級之間都存在顯著差異，表5中*標出了顯著性差別。同樣，側面驗證了基于k-means對不同風險等級的MTTC聚類效果良好。

4 不同風險等級的MTTC概率分布擬合

4.1 概率分布模型參數估計

選用Weibull分布、Gamma分布、對數正態分布3種經典概率分布模型，針對車車通信4種風險等級的MTTC概率分布進行分析。采用MLE參數估計方法對3種模型的參數進行估計，參數估計結果見表6。其中，α1、β1分別代表Weibull分布的形狀參數和尺度參數；α2、β2分別代表Gamma分布的形狀參數和比例參數；μ、σ分別代表對數正態分布的對數均值和對數標準差。

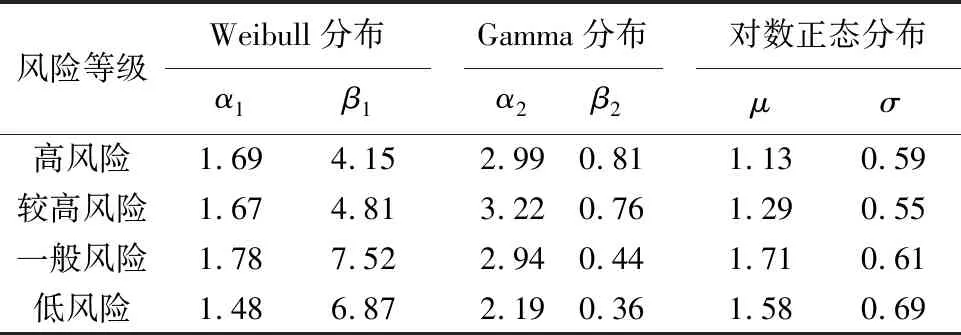
表6 概率分布模型參數估計值

4.2 模型對比和檢驗

選取小于20 s的車車通信MTTC實驗樣本數據，利用上述3種概率分布模型對4種風險等級的MTTC概率分布進行擬合。為了定量比較概率分布模型的擬合效果，選用K-S檢驗對擬合結果進行檢驗，其中p值表示在原假設為真的條件下樣本觀察結果出現的概率。若p很小，則表示原假設情況發生的概率很小。根據小概率原理，拒絕原假設。取0.05作為顯著性水平，如果p大于0.05，認為數據總體樣本分布符合理論分布模型；否則，理論分布模型不能很好地描述數據分布特性。3種模型的檢驗結果見表7。

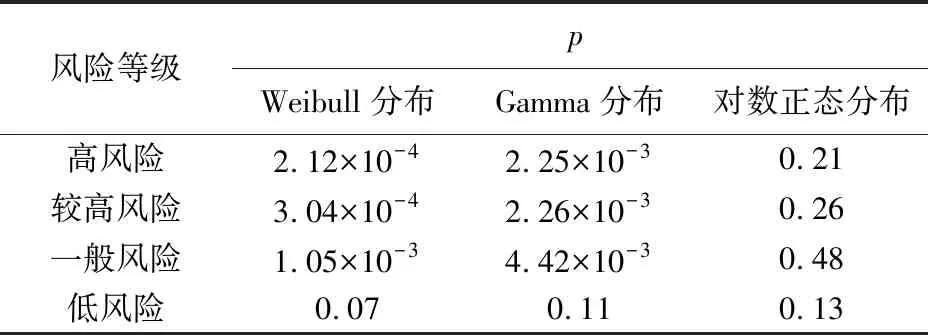
表7 3種模型的K-S檢驗結果

由表7可知，4種風險等級的對數正態概率分布模型K-S檢驗的p值均大于0.05。結果表明，車車通信的高風險、較高風險、一般風險、低風險的MTTC都能夠用對數正態分布進行擬合，而Weibull和Gamma概率分布模型僅能通過低風險等級情形下的假設檢驗。4種風險等級的MTTC分布擬合結果如圖8～11所示。

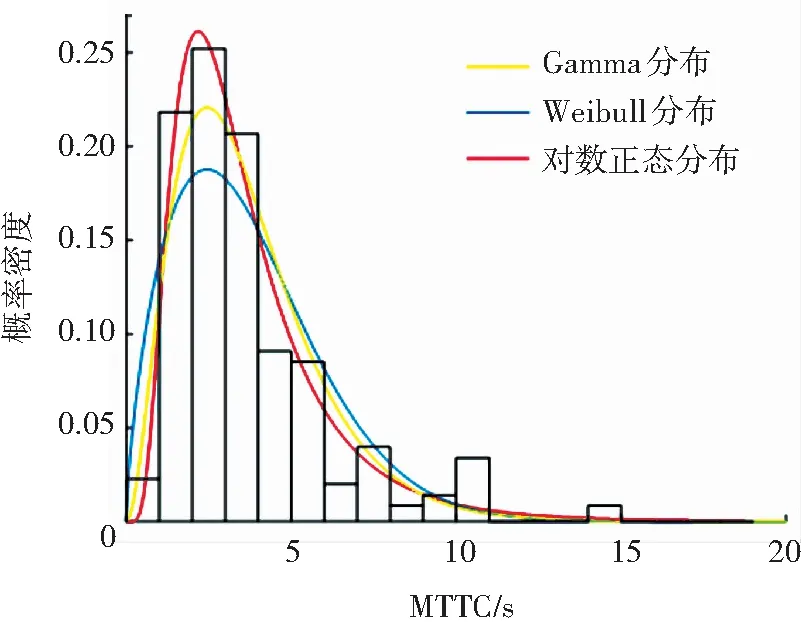
圖8 高風險MTTC分布模型擬合效果對比

圖9 較高風險MTTC分布模型擬合效果對比

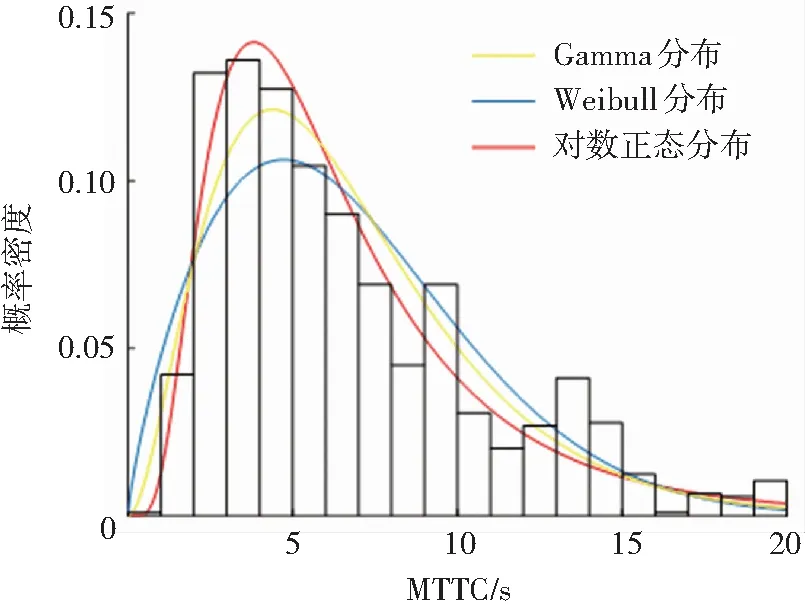
圖10 一般風險MTTC分布模型擬合效果對比

P-P圖表示變量的累積概率與理論模型的累積概率之間的關系。P-P圖中各點越近似一條直線表明理論模型越接近真實概率分布[18]，選擇P-P圖進一步對3種概率分布模型的擬合效果進行分析。圖12～15為4種不同風險等級的MTTC概率分布函數參數擬合的P-P圖。結果表明，對數正態分布優于Weibull分布和Gamma分布，與表7的K-S檢驗結果相一致。

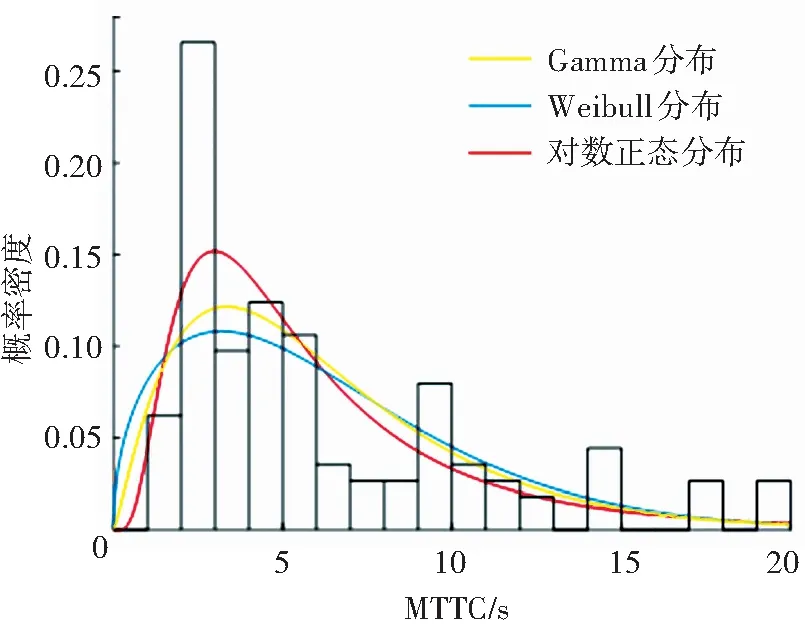
圖11 低風險MTTC分布模型擬合效果對比

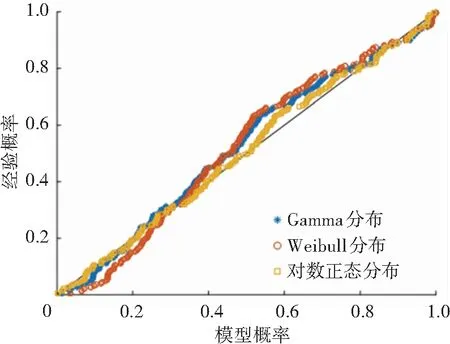
圖12 高風險P-P圖

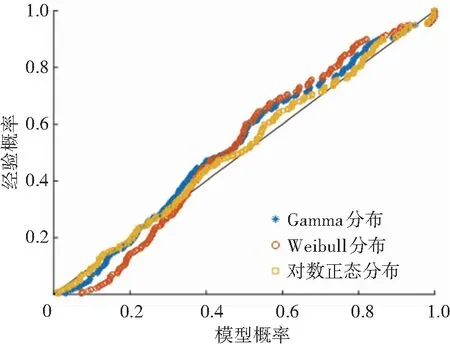
圖13 較高風險P-P圖

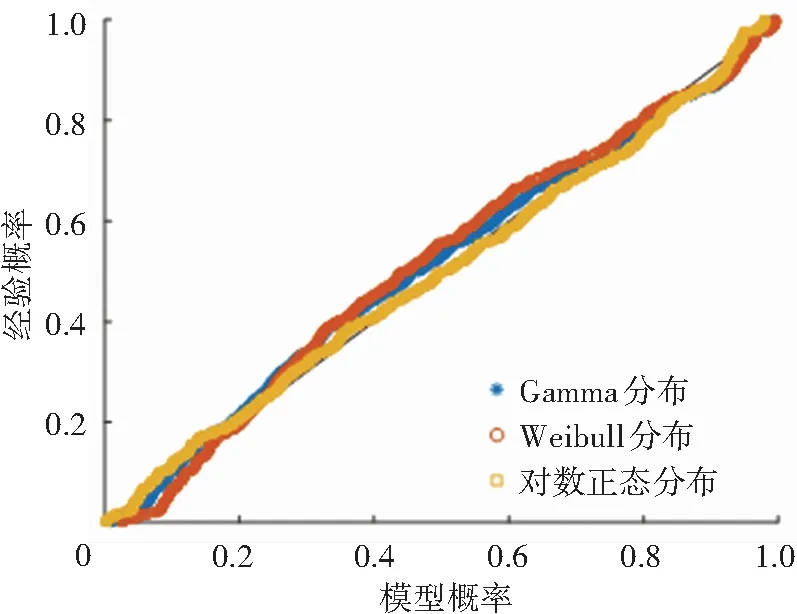
圖14 一般風險P-P圖

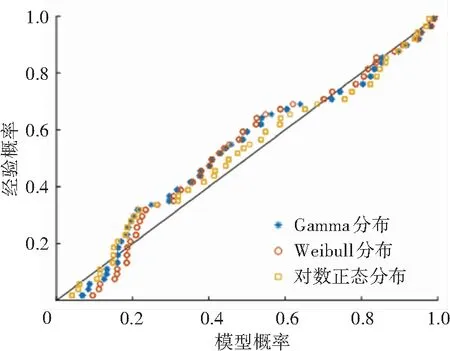
圖15 低風險P-P圖

5 MTTC混合分布模型構建與驗證

5.1 混合分布模型構建

基于上述分析結果可知，對數正態分布對車車通信的4種風險等級的MTTC擬合效果最優。因此，針對4種風險等級，建立描述MTTC總體的對數正態混合分布模型如下：

(9)

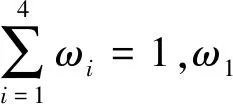
記MTTC的分布模型參數θ=[ω1,ω2,ω3,ω4,μ1,μ2,μ3,μ4,σ1,σ2,σ3,σ4]。

5.2 參數估計

混合分布模型參數估計通常采用EM算法進行求解。

EM算法的迭代分為兩部分，即E步和M步。兩部分交替進行計算。設γji為隱變量，其表達式為

(10)

式中：γji為第j個MTTC樣本對應的第i類分布的隱變量；n為樣本總數。

為方便計算隱變量值，將式(9)記為

(11)

(12)

EM算法的步驟如下：

1)選擇模型參數θ的初始值θ0，開始迭代。

2)E步是由前一次迭代得到的θm，計算隱變量的新值，即

(13)

3)M步是計算新一輪迭代的模型參數，即

(14)

(15)

(16)

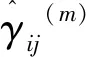
以θm+1作為θm的更新值，重復E步和M步，直至‖θm+1-θm‖小于某個設定值時停止迭代，最終得到分布函數參數的估計值。

5.3 實例驗證

為驗證理論分布模型的合理性和普適性，分別采用車車通信場地實驗和一般環境場地實驗獲取的MTTC<20 s的實驗樣本數據進行驗證。

利用車車通信場地實驗采集的車輛行駛運動學數據，采用EM算法估計概率分布模型參數，并選取Weibull分布、Gamma分布、對數正態分布作為對比模型。

采用K-S檢驗方法對擬合結果進行檢驗，顯著性水平為0.05，車車通信MTTC混合分布模型參數標定及K-S檢驗結果見表8。

由表8可知，對數正態混合分布通過檢驗，說明車車通信MTTC可用對數正態混合分布模型擬合，同時也驗證了4種風險等級之間存在差異性。圖16為車車通信的4種MTTC概率分布模型的擬合曲線。

表8 車車通信MTTC分布模型參數及K-S檢驗結果

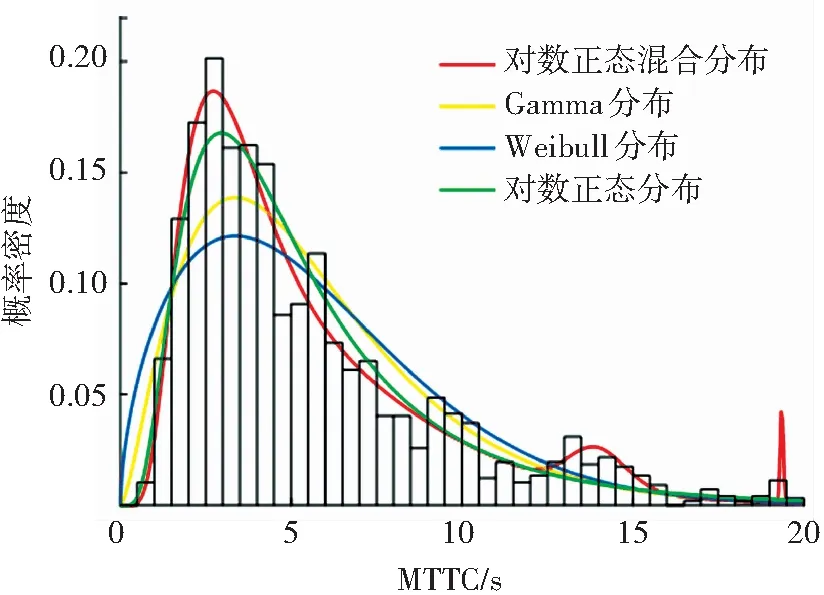
圖16 車車通信 MTTC分布模型擬合效果對比

由圖16可知，與其他3種概率分布模型相比，對數正態混合分布模型擬合的曲線最接近車車通信MTTC概率分布。

利用4種概率分布模型對一般環境下MTTC<20 s的實驗樣本數據進行擬合。對數正態混合分布、Weibull分布、Gamma分布以及對數正態分布的K-S檢驗結果p值分別為0.10、6.28×10-6、4.78×10-3、8.67×10-6。圖17為4種概率分布模型的擬合效果。結果表明，相比其他3種概率分布模型，對數正態混合分布模型也能更好地擬合一般環境下的MTTC分布，進一步驗證了理論分布模型的合理性。

圖17 一般環境 MTTC分布模型擬合效果對比

6 結 論

1)通過車車通信環境場地實驗，獲取實際車輛行駛實驗數據，利用k-means聚類方法劃分了車輛運行風險等級，獲得了不同風險等級的車輛行駛運動學數據。

2)考慮4種車輛運行風險等級，分析了不同類型風險等級的MTTC概率分布規律，對比了3種概率分布模型在不同風險等級下的擬合檢驗效果。

3)建立了MTTC對數正態混合概率分布模型，標定了模型參數，對比了4種概率分布模型，通過擬合優度分析驗證了混合分布模型的有效性。

4)本文針對兩車行駛場景研究了車車通信環境下MTTC概率分布規律，未來應嘗試更高車速多車間的跟馳、換道等駕駛行為的車輛行駛測試實驗，進一步探究符合復雜道路MTTC概率分布規律。