面向復雜網絡的多屬性決策關鍵節點識別算法研究*

寧 陽 武志峰 張 策

（天津職業技術師范大學信息技術工程學院 天津 300222）

1 引言

網絡中的關鍵點識別算法是網絡科學的重要研究內容之一。關鍵點識別算法的研究在醫學、社會學、網絡安全、電力交通、政治與經濟學領域具有重要意義。在社會網絡中通過最有影響力的人的查找，可以控制流言的傳播；在疾病爆發區域通過易感人群的查找，可以對疾病進行有效地預防和控制；在城市交通系統、電力系統中通過對關鍵樞紐的識別和重點維護，可以降低經濟損失風險。對復雜網絡有效管理的關鍵是有效識別網絡中的關鍵結點。目前，解決這一問題的算法通常采用基于圖論的概念和術語，將具體實際問題抽象為圖，進而得到具體實際網絡的拓撲性質。相關研究通常是在常用指標進行改進和將多個指標進行融合［1～4］，因為度中心性［5］算法雖然簡單高效，卻沒有考慮網絡的全局結構；介數中心性［6］、接近中心性［7～8］考慮了網絡的全局結構，但算法時間復雜度高，并不適合在大規模網絡中應用；Kitsak等考慮節點在網絡中的位置，提出k-shell［9］分解方法，能夠適用于大規模網絡，由于網絡中存在大量度值相同的節點，k-shell排序方法的分辨率不高；為解決k-shell方法劃分結果粗粒化的問題，鄧凱旋［10］等提出根據節點刪除過程中迭代層數，結合節點度和鄰居節點，改進k-shell方法識別關鍵節點；李懂［11］等提出融合節點度和K核迭代次數的多屬性決策方法，通過熵權法衡量節點重要性；Liu［12］等提出結合當前節點所在ks值及最大ks值，計算節點到最大K核節點集合的最短距離，進而區分ks值相同的節點；Bae等［13］提出考慮局部范圍內節點的ks值，節點兩層鄰居節點的ks值和，借鑒局部中心性思想改進k-shell；顧亦然等［14］將k-shell與重要度貢獻矩陣相結合，引入影響度的概念進行關鍵節點識別。然而，隨著網絡規模的不斷增大，現有算法在衡量節點影響力的準確性和效率上，均出現了明顯不足，難以應對日益復雜網絡的各類新問題。本文基于節點度、改進的K核迭代次數指標，使用熵權法［15］、灰色關聯度分析法［16］多屬性決策關鍵節點，更有效地進行關鍵節點識別。

2 相關概念

2.1 網絡表示

將一個具體網絡抽象為一個由點集V和邊集E組成的圖G=（V，E）。頂點數記為N=|V|，邊數記為M=|E|。無向無權圖G的鄰接矩陣A=（aij）N×N是一個N階方陣，第i行第j列上的元素aij定義如下：

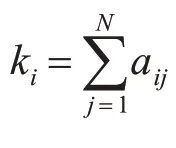
2.2 相關算法

k-殼分解，通過去除網絡中度值為1的節點及其連邊，將過程中產生新的度為1的節點劃分到同一層，直至網絡中每個節點的度值至少為2。重復操作，去除網絡中度值為2的節點及其連邊，直至網絡中不再有度值為2的節點為止。k=1，2，3…，直至網絡中的每一個節點均被劃分到相應的k-殼中，每一個節點對應唯一的ks值，且k-殼中所包含的節點度值滿足ki≥ks。所有ks≥k的k-殼的并集為網絡的k-核［17］。實際網絡中就某些問題而言度大的節點通過k-殼分解的方法，由于具有較小的ks值不一定是重要節點［18］。圖1是由17個頂點組成的小網絡，節點v6的度大于節點v11，ks值小于v11。

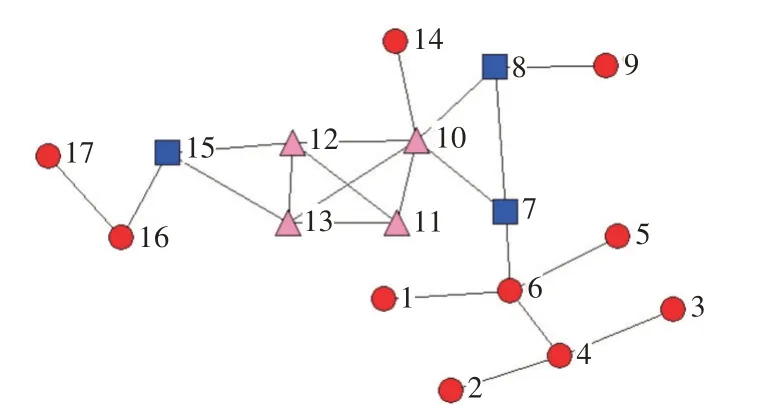
圖1 示例圖三角形節點ks=1方形節點ks=2圓形節點ks=3

其中公式涉及的k（i）為節點度，n（i）為節點迭代次數，Γ(i)為節點i的鄰居節點集合。

文獻［10］通過k-shell分解過程中節點被刪除的順序定義迭代次數增加ks值區分程度，結合節點度衡量節點重要性，該指標值越大，節點越重要，如式（1）所示：

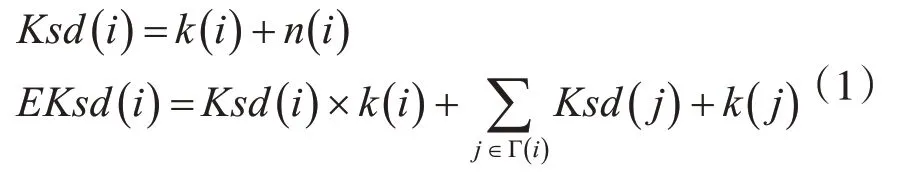
文獻［11］通過熵權法計算節點度值和迭代次數兩個指標的權重w1、w2，計算權重因子Vw，結合節點本身及鄰居節點的權重因子得到節點的綜合重要性值DK（i），如式（2）所示：

文獻［13］提出通過鄰居節點的ks值衡量節點重要性，通過擴展得到Cnc+值，如式（3）所示：

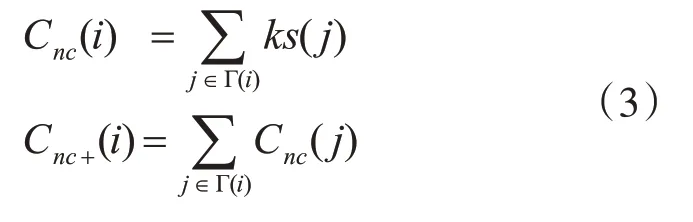
3 k-shell多屬性決策改進算法

3.1 改進K核迭代次數指標

節點度是一種局部性指標，可以反映節點的影響能力，K核迭代次數反映節點的全局位置，計算K核迭代次數時，k-殼分解方法中的節點刪除順序不再從度值小于k，k=1，2，3…累計計算，直到網絡中每個節點都對應唯一一個ks值。改為按照度值刪除度值最小的節點，ks值遞增，計算每個節點的ks值；K核迭代次數是在ks值的基礎上計算得到，剝除網絡中度值小于等于k的節點，若產生新的滿足剝除條件的節點，此時依舊首先去除度值最小的節點，ks值不變，節點刪除的迭代次數累加，節點的迭代次數即被刪除的順序。通過計算節點到最大核節點集的平均距離改進K核迭代次數，進一步區分相同K核迭代次數值，以此劃分節點重要程度，本質為了增加ks值區分程度，解決粗粒化劃分問題。節點度和K核迭代次數為效益型指標［15］。

定義成本型指標節點到最大核節點的平均距離Ave_d和改進后迭代次數值n′，如式（4）所示：

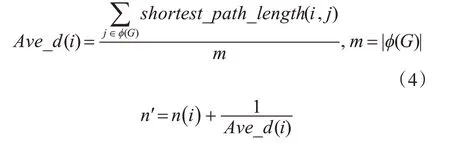
其中，φ(G)為網絡中最大核節點集合。

3.2 構造規范化決策矩陣

通過計算節點的上述指標，構建規范化決策矩陣RM×N，M=2，N為網絡中節點個數。Rij分別表示度值、改進迭代次數標準化后值，i=1，2。

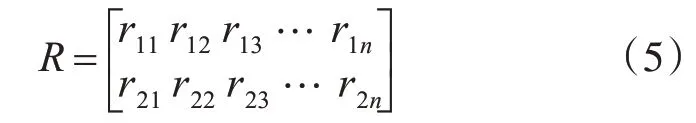
規范化決策矩陣處理方式［15］：

3.3 熵權法確定權重

熵權法根據各項指標所包含的信息量的大小來確定指標權重的客觀賦權法［15，19］。首先對決策矩陣R進行歸一化處理，得到R′，其次計算第i項指標的熵值Evi，如式（8）所示，然后根據熵值Evi計算兩個指標各自權重wi：

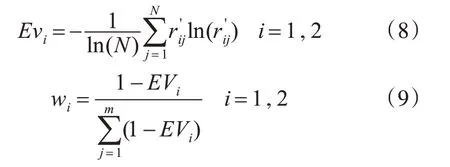
3.4 灰色關聯度分析法確定權重

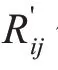
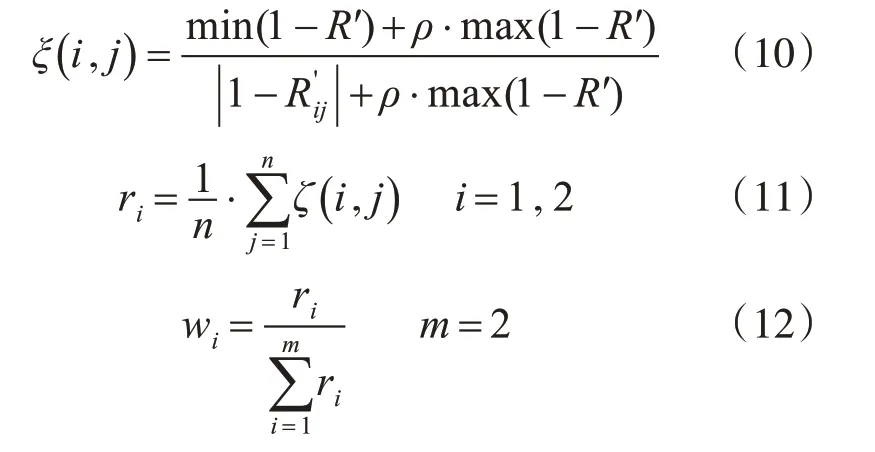
3.5 綜合評估節點重要性

根據wi綜合評估節點重要性：

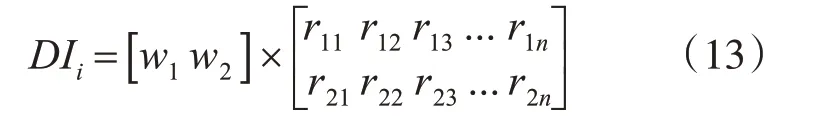
考慮局部信息，結合鄰居節點定義重要性評價指標：

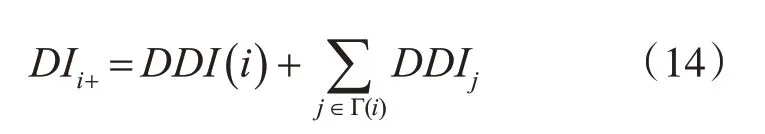
其中，使用熵權法確定權值計算得到的衡量節點重要性指標記為EDI，使用灰色關聯度分析法確定權重方法得到的指標記為GDI。

算法步驟：

1）計算網絡中每個節點的度、改進的迭代次數；

2）分別使用熵權法、灰色關聯度分析法按照式（6）、（7）效益型指標規范化決策矩陣；

3）按照兩種賦權方法計算每個指標的貢獻權重；

4）根據式（14）計算每個節點的EDI、GDI值。

4 實驗分析

4.1 評價標準

4.1.1 單調性指標

本文算法為了解決k-shell方法劃分結果粗粒化問題，使網絡中的節點盡可能分配單一排序等級，排序相同值的節點少，單調性指標值越大。采用文獻［11］中方法評價不同排序方法的單調性。Monotonicity定義如下：

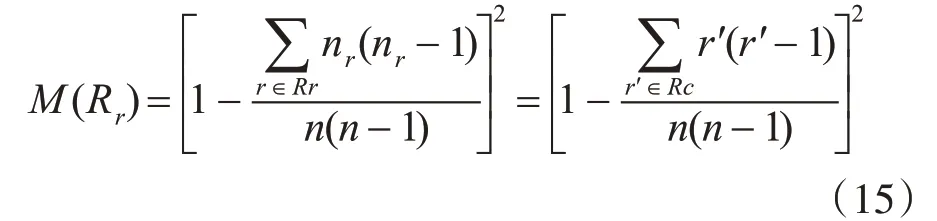
其中Rr為排序等級列表，n為排序結果中元素數目，nr為相同等級節點數目。為簡化計算，Rc為劃分到相同等級中節點個數非1的列表，該指標公式用于衡量排序結果中相同值所占列表比例。

4.1.2 相關性指標

本文使用SIR傳播模型獲得標準排序結果，N個節點的狀態可分為三類。

1）S：易染狀態，初始條件下所有節點均為易染狀態，該節點以β的概率被鄰居節點感染；

2）I：感染狀態，感染某種病毒作為傳染源的節點，該個體以β概率感染其鄰居節點；

3）R：移除狀態，也成免疫狀態或恢復狀態，感染狀態節點以β概率感染鄰居易感節點后，以γ概率變為R移除狀態，不再具有感染能力和易感特性；

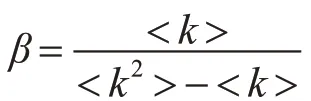
使用Kendall相關系數τ計算兩個排序序列list1和list2之間的相似性，定義如下：

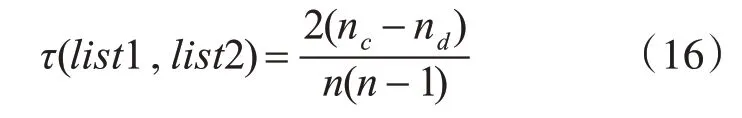
其中，nc表示兩個序列中同序對的個數，nd表示兩個序列中異序對的個數，n表示排序序列列表的長度。τ值越大，兩個列表之間相似性越大。

例：list1=｛1，2，3，4｝，list2=｛1，3，2，4｝。

表1 list1與list2二元組集合

4.2 仿真實驗

根據上述分析，為了驗證本文提出方法的有效性及準確性，設計兩組對比實驗，在六個網絡數據集進行仿真實驗，并與Ks、Cnc+、EKsd、DK算法指標進行對比分析，比較算法排序結果單調性；使用SIR傳播模型計算標準排序結果，計算各中心性算法與SIR的Kendallτ相關系數；比較熵權法、灰色關聯度分析法確定權重的計算方法的差異。具體網絡拓撲結構統計特征如表2所示。

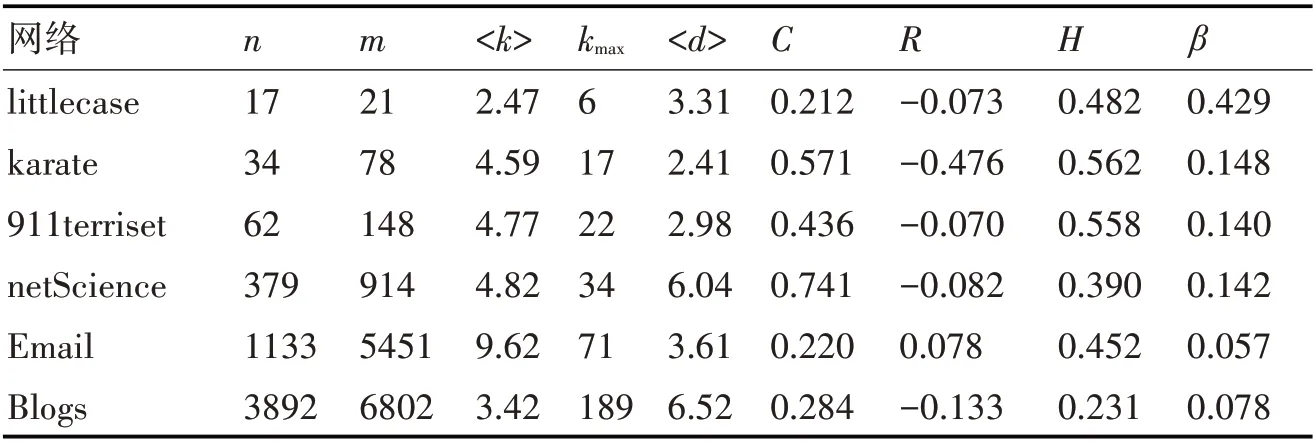
表2 網絡拓撲結構統計特征

littlecase為一個案例網絡，karaze［20］是具有社團結構的網絡，由美國一所大學的空手道俱樂部成員組成的關系網；911terriset［21］網絡是恐怖襲擊網絡，每個節點代表一名恐怖分子，節點之間的邊代表恐怖分子之間的聯系；netScience［22］是科學家合作網絡，網絡代表科學家之間的合作關系，本文選取網絡中的極大連通子圖；Email［23］網絡是電子郵件收發網絡，聯系人之間發送過郵件產生一條邊；Blogs［23］網絡是MSN上的博客網絡，當一個人在另外一個人的博客有評論時，產生一條邊。上述網絡均按照無向無權網絡處理，＜k＞表示網絡平均度，即網絡中所有節點度的平均值，kmax表示節點最大度，＜d＞表示網絡節點間最短路徑平均數，C表示聚類系數，用來評估節點聚集成團的集聚程度；R表示同配系數，用來反映鄰接節點間的度相關性；H表示異質系數，衡量網絡中節點度分布的異質［24～25］。β表示SIR傳播模型中的感染概率。

表3展示了ks、Cnc+、EKsd、DK及本文提出的兩種確定權重方法GDI和EDI分別在上述六個數據集仿真實驗進行關鍵節點識別，排序結果的單調性分析，由表可知，k-shell方法在三個數據集上的單調性驗證結果均是最差，存在粗粒化劃分問題。本文提出的使用到最大核節點的距離改進迭代次數，兩種權重賦予方式提出的GDI、EDI方法單調性驗證結果排名Top2，且GDI單調性優于EDI。說明兩種賦予權重的方法均能夠有效地解決k-shell劃分結果粗粒化的問題，使得更多的節點被劃分到不同的等級。

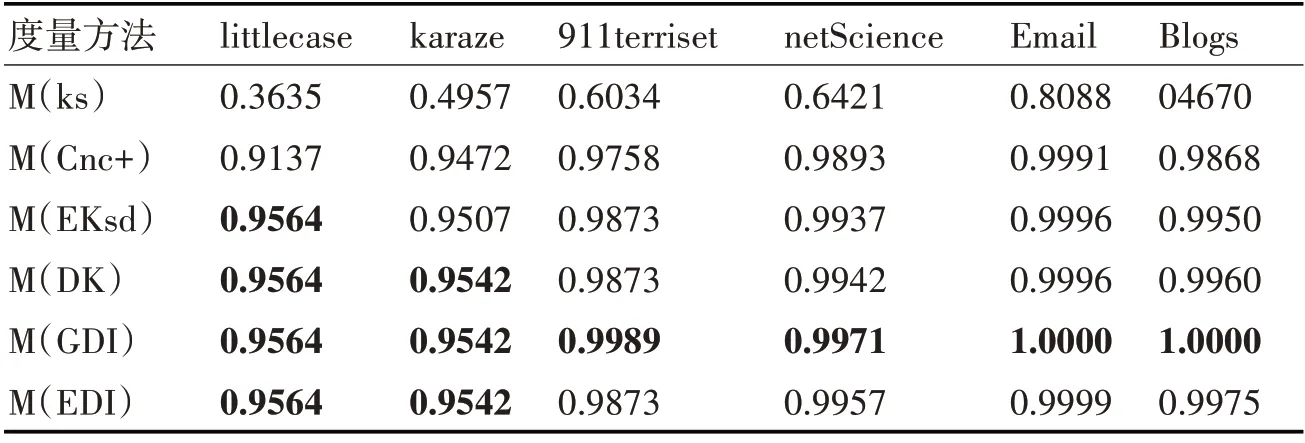
表3 不同度量節點單調性分析表

表4展示了ks、Cnc+、EKsd、DK、GDI和EDI算法分別在六個數據集的關鍵節點識別結果，與SIR仿真傳播確定節點傳播能力的節點重要性之間的相關性，通過數學計量Kendall相關系數體現相關性差異，本文算法EDI在六個數據集上均與SIR傳播模型相關系數值最大，相關性最強，最貼近標準排序結果。EDI算法在DK算法基礎上考慮節點到最大核節點的平均距離，改進K核迭代次數，使用熵權法確定權重，在上述六個數據集中，單調性和有效性均優于其他算法。GDI算法使用灰色關聯度分析法確定權重進而計算節點重要性指標，但是從表4算法有效性中看出，該方法在部分數據集上優于相同貢獻度的EKsd算法、熵權法確定權重的DK算法，如karate數據集、net Science數據集，在部分數據集上與SIR傳播模型標準排序差異很大，如Blogs網絡。因為在使用灰色關聯度分析法確定權重時，對于所有網絡人為主觀決定分辨系數ρ取定值0.5，取值的不同會最終影響權重的分配，使得算法可信度降低。所以采用熵權法確定權重可以更有效地進行關鍵節點識別。

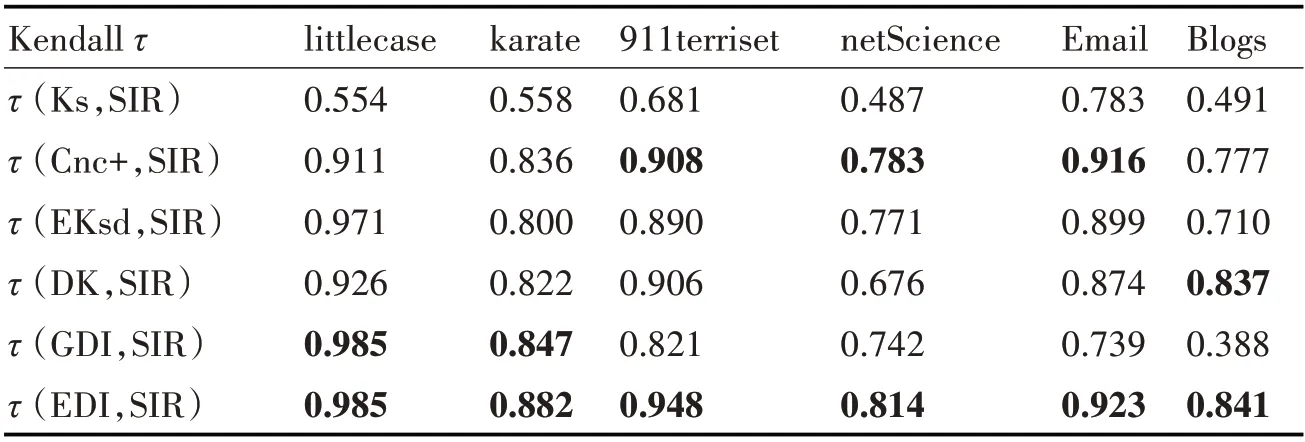
表4 不同度量指標相關性分析表

5 結語

本文算法主要解決復雜網絡中關鍵節點識別問題中，k-shell識別方法帶來的粗粒化劃分問題，融合網絡局部信息和全局信息，更全面地識別網絡中的關鍵節點，通過節點到最大核距離改進K核迭代次數、融合節點度，使用熵權法確定權重，結合鄰居節點的貢獻，更有效地識別無向無權網絡中的關鍵節點。實驗證明，GDI算法雖然在單調性方面明顯優于其他方法，但EDI算法在有效性上明顯優于其他方法，能夠以較高精度識別出網絡中的關鍵節點。下一步計劃將點權強度融合到本文算法擴展到加權網絡，進一步對灰色關聯度分析方法中的參數ρ進行深入研究。