基于粒子濾波的一維非恒定流模擬多變量校正方法

顧爐華，賴錫軍

(1.江蘇省環境科學研究院，江蘇 南京 210036; 2.長江勘測規劃設計研究有限責任公司上海分公司，上海 200439; 3.中國科學院南京地理與湖泊研究所，江蘇 南京 210008)

為減少數值模型的不確定性，數據同化方法被引入到水文、水動力模型[1-2]。數據同化方法可分為確定性方法和不確定性方法，前者由果及因，根據已知結果反推未知參數，代表方法有變分法[3-4]；后者基于統計估值理論，通過實時融入觀測實現預報場的動態更新，代表方法有卡爾曼濾波和粒子濾波算法[5-6]。卡爾曼濾波及其改進算法以其在高維度、非線性系統中的良好表現在水文預報領域得到應用與發展，成為實時校正的主流技術之一。但這些算法都假設噪聲在空間上為零均值高斯分布，在非高斯系統中應用會出現濾波發散問題。而粒子濾波算法能很好地解決這一問題，粒子濾波又叫順序蒙特卡羅濾波，是對貝葉斯估值理論的一種蒙特卡羅算法實現。與經驗方法、優化插值、連續方法等傳統實時校正方法及集合卡爾曼濾波方法相比，粒子濾波算法的優勢主要體現為：不受高斯分布假設的約束、能更好表現非線性系統的變化信息、計算效率高、算法容易實現等[7-10]。

關于粒子濾波方法應用于水力學模型的研究目前主要集中在濾波參數選擇、算法結構完善、洪水預報等方面。Moradkhani等[11]運用粒子濾波對模型狀態變量及參數展開了不確定性分析；Nohs等[12]提出了基于粒子濾波的狀態變量和參數同步更新算法；畢海蕓等[13-16]提出了殘差重采樣、分層重采樣、聚合重采樣等方法，進一步完善了粒子濾波的性能；楊瑞祥等[17]和徐興亞等[18]分別將粒子濾波應用于水文模型和水動力模型進行洪水預報，對濾波的實用性進行了進一步驗證。這些成果豐富了粒子濾波方法的理論和應用。

本文將粒子濾波方法引入一維非恒定流模擬計算中，建立一維水量模擬的多變量校正方法，分析粒子數量、狀態變量擾動誤差標準差和邊界條件的不確定性對濾波性能的影響，比較粒子濾波與集合卡爾曼濾波的性能，為粒子濾波方法在河網水量分析、洪水預報等實際應用提供技術支撐。

1 粒子濾波基本原理

1.1 貝葉斯濾波原理

貝葉斯濾波利用觀測數據來構造系統狀態的后驗概率密度，利用狀態轉移模型估計系統狀態的先驗概率密度，再結合最新的觀測數據對先驗概率密度進行修正，繼而得到系統狀態的后驗概率分布。

首先，建立狀態方程和量測方程：

Xk=AXk-1+BUk+Wk

(1)

Zk=Hk+Vk

(2)

式中：Xk為k時刻系統的狀態量；Uk為k時刻系統的控制量；A、B為狀態系統參數矩陣；Zk為k時刻的觀測量；Hk為k時刻量測系統的觀測矩陣；Wk、Vk分別為k時刻狀態系統和量測系統的噪聲。

假設狀態系統Xk服從一階馬爾科夫過程且量測系統Zk獨立，那么根據條件概率理論，式(1)可表達為先驗概率p(Xk|Zk-1)，式(2)可表達為似然概率p(Zk|Xk)。由貝葉斯條件概率公式，可推出后驗概率p(Xk|Zk)的表達式：

(3)

在實際應用中，大多數的后驗概率密度都是很難直接進行解析的，為此引入多重積分的蒙特卡羅方法。

1.2 蒙特卡羅方法

蒙特卡羅方法的核心思想是把待求解的問題抽象為隨機事件，通過從已知的概率分布中隨機抽樣，實現對所求問題的解的近似估計。蒙特卡羅方法的理論基礎是大數問題，當樣本足夠大時，蒙特卡羅估計就等同于貝葉斯后驗概率密度。

從p(Xk|Zk)中隨機抽取獨立分布的N個樣本{Xk1,Xk2,…,XkN}，狀態系統的后驗概率密度分布可近似表示為

(4)

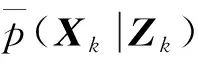
1.3 粒子濾波方法

粒子濾波方法是用蒙特卡羅方法求解貝葉斯后驗概率密度的方法，它將每一個樣本視作一個粒子，以似然值作為粒子的權重，通過對粒子加權平均得到后驗概率密度。粒子濾波可分為4步：模型預報、重要性采樣、重采樣和粒子擾動。

模型預報是在生成若干個水流狀態粒子后，基于數學模型驅動各個粒子平行計算，得到每一個時刻水流狀態的預報值。

粒子濾波基于序貫重要性采樣，即在蒙特卡羅思想中應用統計學理論中的序貫分析方法，以遞推得到后驗概率密度函數的最優估計。其實現方式是計算每個粒子的似然值，并將其歸一化。本文采用如下似然函數：

(5)

式中：wki為k時刻第i個樣本的似然值；σ為相對標準差。

在粒子權重更新的過程中，不可避免地會出現“粒子退化”現象，造成大部分計算資源都用在權重很小的粒子上，因此需要用到重采樣技術，其本質是復制大權重粒子，剔除小權重粒子，本文采用多項式重采樣，其原理見文獻[19]。

重采樣之后，需再次對粒子群施加擾動，保證粒子群在大權重粒子占多數的情況下仍有一定的多樣性。本文采用如下擾動方法:

X(i)=X(i)(1+N(i)σ)

(6)

式中：X(i)為第i個河道斷面的狀態量；N(i)為第i個河道斷面的偽光滑隨機擾動場，服從均值為0、方差為1的正態分布。

2 基于粒子濾波的一維非恒定流水量校正模型

2.1 一維非恒定流模型

本文建立的一維非恒定流模型基于圣維南方程組：

(7)

(8)

式中：Z為水位，m；Q為流量，m3/s；K為流量模數；m3/s；q為單位河長旁側入流，m2/s；A為過水斷面面積，m2；α為動量校正系數；g為重力加速度，m/s2；x為沿水流方向距離，m；t為時間，s；B為水面寬度，m。

采用Preissmann四點加權隱格式離散上述兩式得到：

A1jΔQj+B1jΔZj+C1jΔQj+1+D1jΔZj+1=E1j(9)

A2jΔQj+B2jΔZj+C2jΔQj+1+D2jΔZj+1=E2j(10)

式中符號的含義可見文獻[20]。對于緩流，在已知上下游邊界條件的情況下，可用追趕法求出各系數，進而求得河道各斷面每一時刻的水位值和流量值。

2.2 水量校正模型算法流程

首先對水位和流量施加隨機擾動，生成N個水流狀態粒子；沒有觀測數據融入的時刻，驅動粒子進行并行計算，形成粒子群搜索空間；在有觀測數據輸入的時刻，啟動粒子濾波模塊，對觀測數據的類型及誤差進行分析；計算每個粒子與觀測之間的似然值，得到粒子權重；接著對粒子群進行多項式重采樣，計算粒子的平均值并輸出。圖1為第k時段內粒子濾波水量校正模型算法流程。

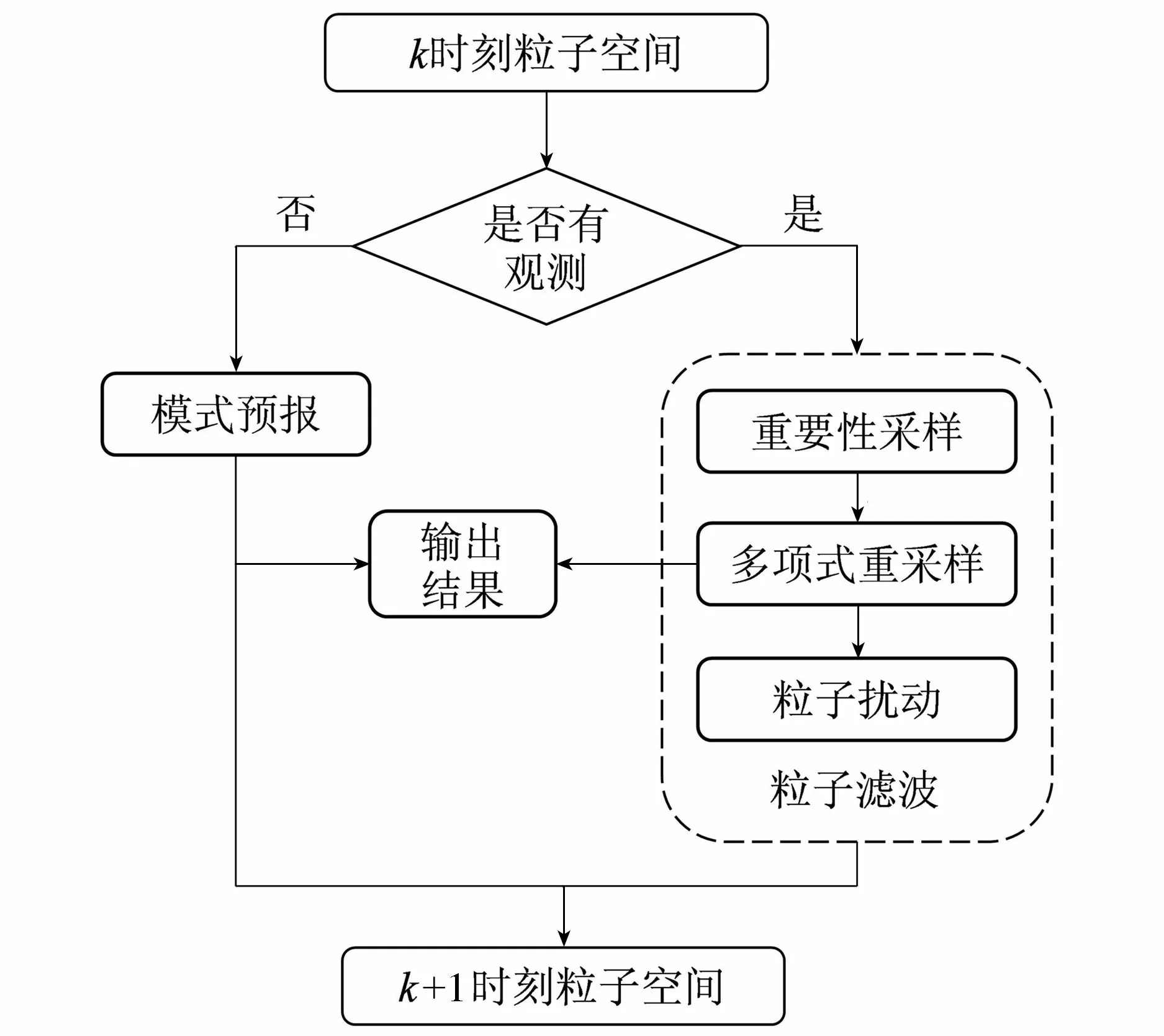
圖1 基于粒子濾波的水量校正模型算法流程(第k時段內)

3 合成數值試驗

3.1 案例選擇

為分析粒子濾波在非恒定流計算中的應用性能，以單一河道洪水演進過程為例開展合成數值試驗。該河道全長60 km，上游給定流量邊界，下游給定水位邊界。共設置4個觀測站點，分別布置在距離上游11 km、23 km、35 km和47 km處，觀測時間間隔為0.5 h。

3.2 試驗設計

選擇沿程斷面水位和流量組成的矩陣作為水流狀態粒子，將上游來流過程作為主要的誤差源，將其按比例縮放作為上游預報洪水過程，研究粒子濾波在不同預報誤差和粒子擾動誤差標準差下的校正性能。將模型在實際流量過程下的計算結果作為真實值，從中抽取水位、流量作為觀測數據。此外，本文計算了上游預報洪水過程下純水動力模型的計算結果作為河道預報水位，與數據同化結果進行對比，以檢驗粒子濾波對水動力模型精度的改善效果。從粒子數量、邊界條件縮放系數、水位和流量擾動誤差標準差4個方面設置計算條件，開展情景計算，各試驗相關參數見表1。

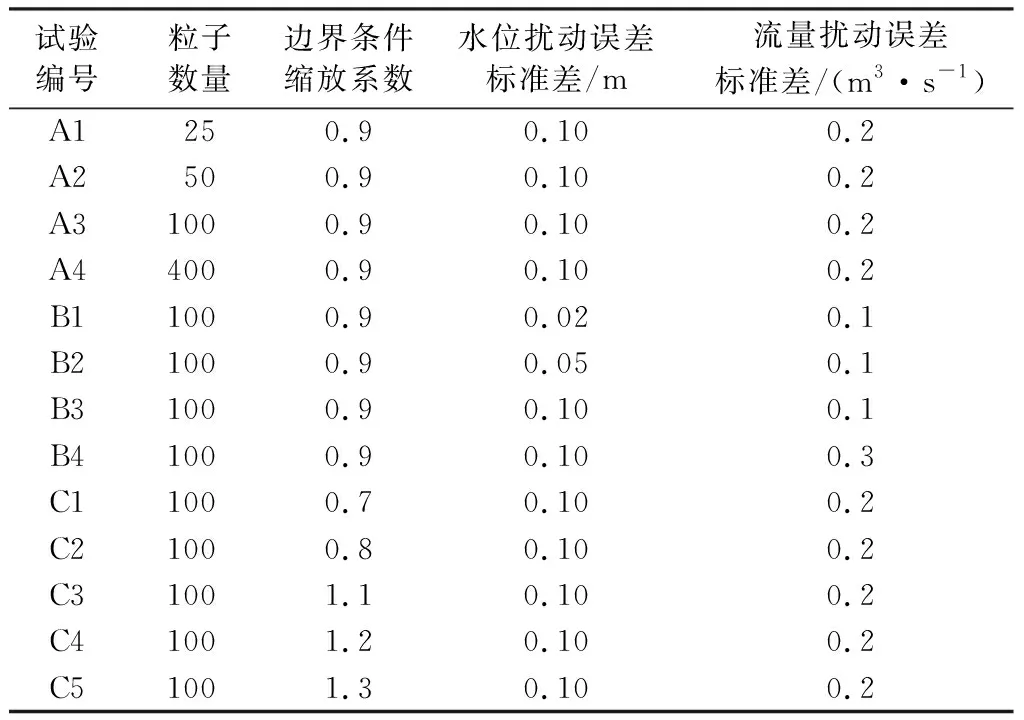
表1 各試驗參數值

3.3 試驗結果與分析

3.3.1粒子數量對粒子濾波的影響

試驗A1～A4的結果顯示，粒子數量越多，流量殘差和水位殘差越小。從圖2可以看出，當粒子數量小于100時，流量和水位殘差隨粒子數量呈快速下降趨勢；當粒子數量大于100后，流量和水位殘差減小的速度減緩。粒子數量為100時，流量和水位殘差分別為17.54 m3/s和0.083 m。更大的粒子數量雖然可以帶來更好的效果，但是也會意味著更大的計算量。在本算例中，粒子數量取100可同時滿足計算精度與效率的要求。

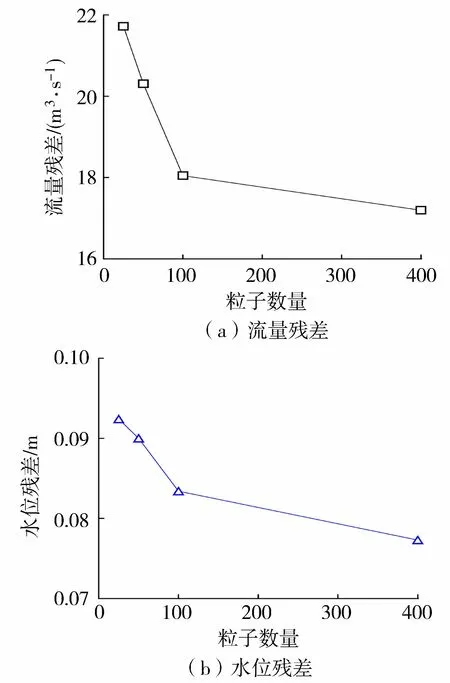
圖2 不同粒子數量下水位和流量殘差

3.3.2擾動誤差標準差對粒子濾波的影響

狀態變量擾動誤差決定了粒子群搜索空間大小和粒子群分布密度。搜索空間太小將限制粒子活動范圍，使其無法到達真實值附近；搜索空間太大又會造成粒子群分布密度降低，真實值周邊缺乏有效粒子。采用純水動力模型的計算結果(預報值)獲得的水位殘差為0.160 m，流量殘差為35.45 m3/s，水位精度為0.950，流量精度為0.942。測試結果顯示，試驗B3中參數設置對發揮粒子濾波效果最有利，水位殘差和流量殘差分別為0.078 m和17.37 m3/s，較預報值情況下降低了約50%，水位和流量模擬精度達到99%(表2)。

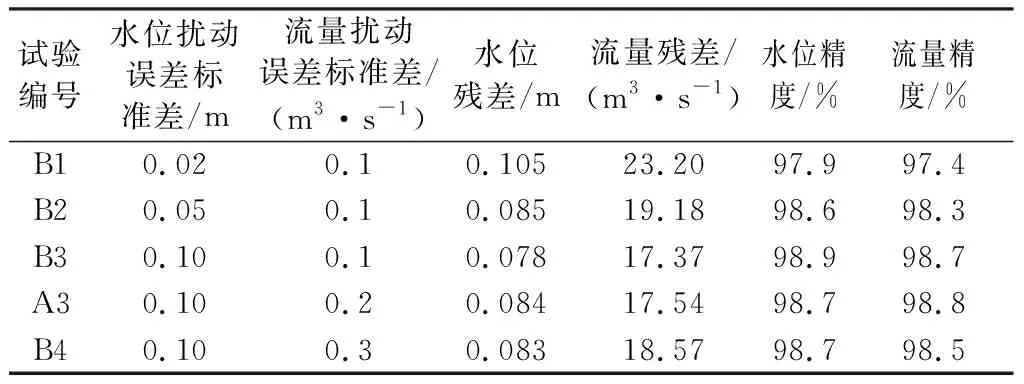
表2 不同擾動誤差標準差下水位和流量殘差統計

3.3.3邊界條件對粒子濾波的影響

由表3可知，當邊界條件縮放系數取0.9和1.1時，水位殘差分別只有0.08 m和0.07 m，對應的流量殘差均小于20 m3/s；當邊界條件縮放系數取0.7和1.3時，水位殘差均達到0.26 m，流量殘差分別高達54.54 m3/s和64.57 m3/s。平均納什效率系數(NSE)也顯示，當邊界條件相對誤差在20%以內，即邊界條件縮放系數在0.8～1.2之間時，粒子濾波效果較好，模擬精度可達94%以上；當邊界條件相對誤差大于20%時，濾波后精度小于90%(表3)。

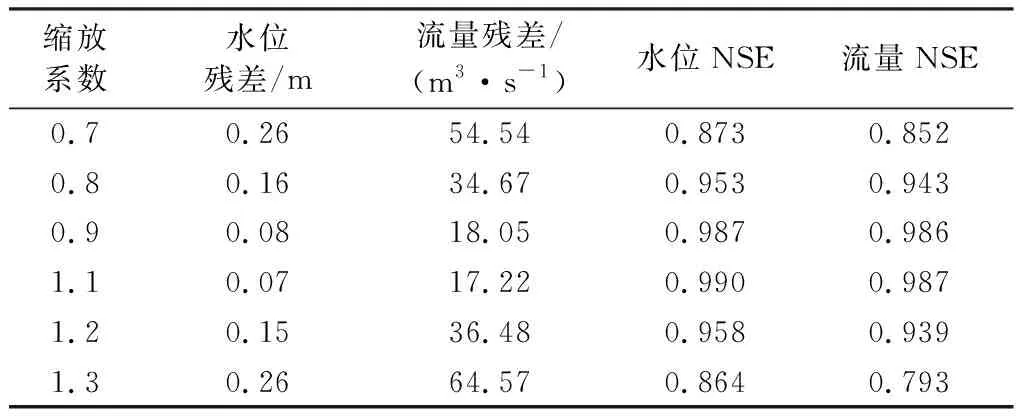
表3 不同縮放系數下水位和流量殘差統計

3.3.4粒子濾波與集合卡爾曼濾波的比較

將粒子濾波與文獻[6]中基于集合卡爾曼濾波的多變量交替校正方法進行對比，為保證結果的合理性，模型邊界條件、狀態變量擾動誤差標準差、集合與粒子個數等主要參數均保持一致。選取距上游邊界10 km(斷面1)、30 km(斷面2)、50 km(斷面3)3個斷面流量過程作為比較對象，總體而言，粒子濾波與集合卡爾曼濾波都具有很好的濾波效果，3個斷面的平均流量預報精度分別達到了98.4%和98.8%，集合卡爾曼濾波算法在結果的準確性和穩定性上更具優勢，洪峰時刻采用集合卡爾曼濾波分析出的洪峰流量比粒子濾波更接近真實值；洪水后期，采用粒子濾波分析出的流量圍繞真實值上下波動，而采用集合卡爾曼濾波獲得的流量與真實值緊密貼合(圖3)。粒子濾波由于無需進行復雜的矩陣計算，從而具有更高的計算效率。在本文使用的案例中，使用集合卡爾曼濾波算法完成一次洪水過程的水量校正需要的CPU時間為883 s，而粒子濾波只要379 s，計算效率約是前者的2.3倍。

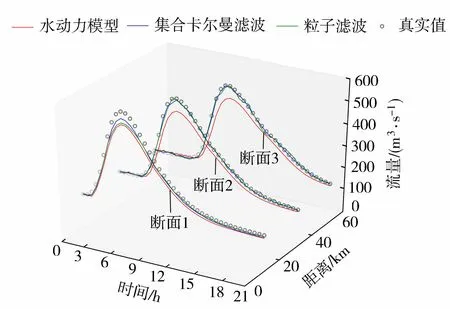
圖3 不同河道斷面流量過程比較

4 實例驗證

4.1 案例選擇

選取太湖流域河網水量模型對粒子濾波的實際應用性能進行驗證，驗證時段為2012年全年。以河網節點水位作為狀態變量，以太湖(西山)、常州、金壇、溧陽等13個站點的逐日實測水位作為更新模型狀態的觀測資料，水位擾動誤差標準差取為實際值的5%，考慮到模型計算量過大，為減少計算時間，本案例中將粒子數取為50。這種選擇雖會在一定程度上減弱濾波效果，但是不妨礙驗證粒子濾波算法在太湖河網水量同化中應用的有效性。太湖流域河網及水文站分布見圖4。

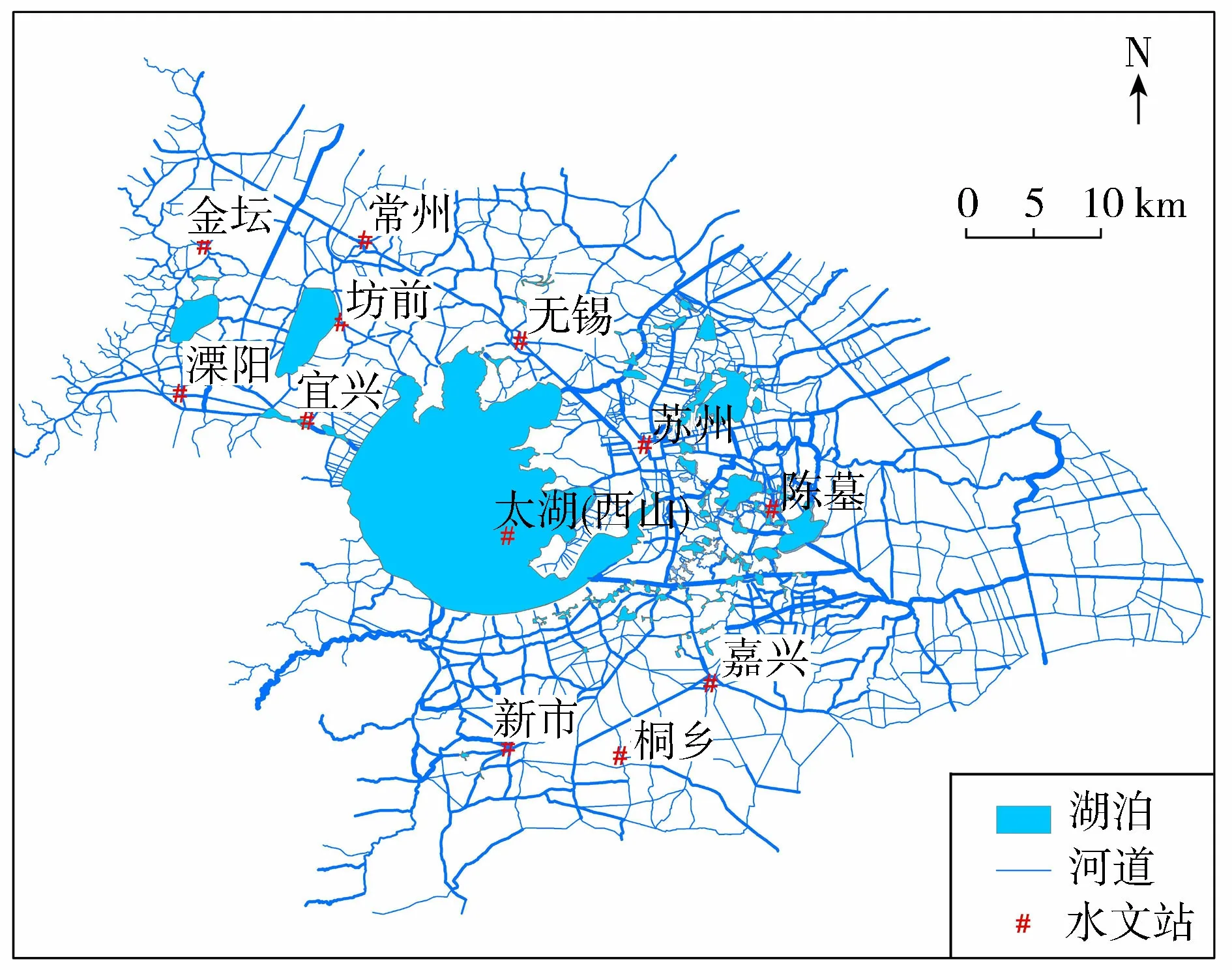
圖4 太湖流域河網及水文站分布

4.2 計算結果與分析

平原河網地區河道多為往復流，流量站少于水位站，且大型水利樞紐多以水位作為調度控制指標，水位對流域水資源的管理與調度更具意義，因此本次分析僅關注流域水位過程。

河網概化、邊界條件、閘站調度等方面的不確定性使得太湖流域河網水量模型模擬出的太湖(西山)、溧陽、蘇州、新市4站的水位與實測值存在較大差距。濾波后的模擬效果有了很大改善，但是不同站點的改善效果存在差異(圖5)。太湖(西山)站、溧陽站和蘇州站濾波效果較好，濾波后的水位與實測水位十分吻合，水位殘差從濾波前的0.17 m、0.40 m、0.10 m分別降為0.05 m、0.10 m和0.05 m，納什效率系數也分別達到了91%、82%和84%；新市站的濾波效果稍差，濾波后的水位仍低于實測水位，但相比于河網水量模型預報結果，水位殘差從0.29 m降至0.18 m，降幅為38%。總體而言，粒子濾波應用于實際河網水量校正可有效改善模擬精度。

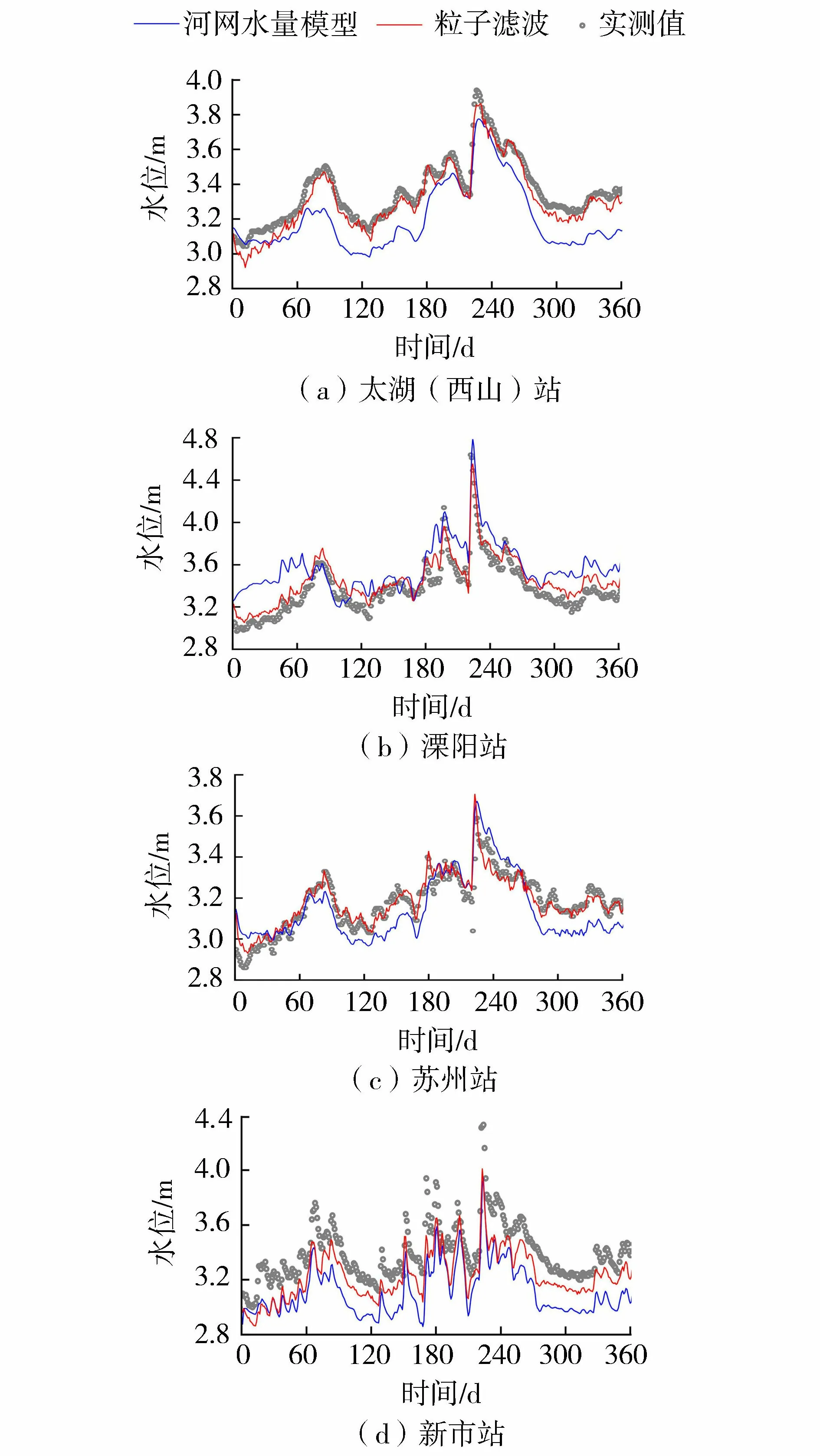
圖5 主要水文站水位過程對比

5 結 語

本文建立了基于粒子濾波的一維非恒定流水量校正模型，通過對水流狀態粒子進行統計估值，實現模型狀態變量的最優估計。探討了多變量校正方法在一維非恒定流計算中的性能，并分析了粒子數量、狀態變量擾動誤差和邊界條件的不確定性對濾波效果的影響。結果證實了粒子濾波可顯著改善模擬精度，且具有較高的計算效率。