基于一維卷積神經網絡的電力系統暫態穩定在線評估

齊 放

(中國廣核新能源控股有限公司, 北京 100000)

0 引 言

近年來，由于暫態失穩所引發的電力系統事故時有發生，對社會和經濟產生極大的危害。然而，傳統電力系統暫態穩定計算基于時域仿真，包含復雜的微分代數方程，在大電網中計算復雜，難以進行暫態穩定在線評估與風險預警[1-4]。

近年來，機器學習技術被引入電力系統暫態穩定評估中，通過非線性方程替代復雜微分代數方程計算，加速暫態穩定評估速度，以滿足在線應用需求。文獻[5]提出了暫態穩定安全域的概念，并在安全域下提出基于多支持向量機的綜合電力系統暫態穩定評估方法，可減少暫態失穩場景的誤判。文獻[6]中離線數據通過相量測量單元PMU采集得到，并通過串行集成多棵回歸樹構建基于XGBoost的暫態穩定預測模型，實現暫態穩定特征重要度排序關系，提高了模型的可解釋性。文獻[7]將概率神經網絡和徑向基函數神經網絡結合，形成復合神經網絡，并用于故障臨界切除時間裕度的預測，提升預測精度。文獻[8] 將深度置信網絡作為黑盒模型擬合發電機出力和系統暫態穩定系數間映射關系，實現暫態穩定評估。文獻[9]直接基于底層數據，將堆疊自動編碼器引入電力系統暫態穩定評估中，采用“預訓練-參數微調”的兩階段學習方法和稀疏化技術提升暫態穩定評估準確度。

下面提出一種基于一維卷積神經網絡(one dimensional convolutional neural network, 1DCNN)的電力系統暫態穩定在線評估方法，將在圖像學習中廣泛應用的卷積神經網絡(convolutional neural network, CNN)引入電力系統暫態穩定評估中，相較于傳統神經網絡方法，有更強的抽象擬合能力，并且1DCNN是傳統CNN的一維形式，更適合電力系統數據的學習。

1 樣本生成

1.1 馬爾可夫鏈蒙特卡洛抽樣

馬爾可夫鏈是一個序列模型，其中數據樣本之間存在依賴關系，且時刻t的狀態概率只與前一時刻t-1的狀態有關。在馬爾可夫鏈中有狀態轉移矩陣，狀態概率矩陣本身通過一定次數的矩陣乘法后，轉移矩陣每一行的概率會趨向于穩定的值，稱為馬爾可夫鏈的平穩分布，即[10-12]：

P(xt∣xt-1,xt-2,…,x1)=P(xt∣xt-1)

(1)

(2)

式中：P為狀態轉移矩陣；x為樣本；π為平穩概率分布；n為轉移次數，當接近無窮時，P接近π，即達到平穩分布。

馬爾可夫鏈蒙特卡洛抽樣算法(Markov chain Monte carlo sampling algorithm，MCMC)是馬爾可夫鏈和蒙特卡洛抽樣的結合。設給定的初始樣本為x0，根據馬爾可夫鏈的收斂性質，經過一定次數的矩陣連乘后，x的采樣概率都會收斂到一個平穩分布，設為π(x)，則后續所有樣本均服從概率分布π(x)。MCMC是從xn+1開始的采樣(設n為矩陣連乘次數)：

(3)

式中，x*為新樣本。πt+1(x*)和πt+1(x)同分布。

實際中采用經典的MCMC采樣的Metropolis Hasting算法進行采樣：

1)初始化：初始化t0時刻樣本為x0，所需抽樣的樣本總數為M。

2)循環：

(1)從均勻分布U(0, 1)中采樣u；

(2)從概率分布q(x*|xi)中采樣樣本x*；

則xi+1=x*，否則xi+1=xi；

(4)當所生成樣本數達到M，結束循環。

3)結束：得到基于MCMC采樣的Metropolis Hasting算法采樣結果。

1.2 基于MCMC的電力系統運行數據生成

電力系統包括PV節點、PQ節點和Vθ節點，以電力系統潮流計算和時域仿真計算的初始參數為所需抽樣的特征參數，因此所考慮的電力系統特征包括：發電機有功出力、發電機節點電壓、有功負荷和無功負荷。根據所研究電力系統模型的特征，設置各個特征變量的取值范圍，然后通過MCMC抽樣算法抽樣海量的電力系統運行數據。基于MCMC的抽樣結果可以使電力系統特征在取值范圍內分布更加均勻，增加樣本的代表性，有助于提高1DCNN模型的泛化性能。

根據以往經驗，對系統模型設置短路類型、故障位置以及故障切除時間，并執行時域仿真計算，得到對應的發電機最大功角差。最大功角差超出180°即視為失穩，否則認為系統穩定。若故障數量為N，則單個電力系統運行數據包括N個最大功角差，分別對應不同的故障[13]。

2 基于1DCNN的暫態穩定評估

2.1 一維卷積神經網絡

CNN是一種前饋神經網絡，它的人工神經元可以對一定覆蓋范圍內的輸入特征進行響應，在大型圖像處理中性能突出。CNN由一個或多個卷積層、線性整流層、池化層和頂端的全連通層組成。1DCNN是CNN的一維形式，被普遍應用于序列數據識別中，更適合電力系統狀態特征向量的識別，相比于傳統神經網絡方法，具有更高的擬合準確度和更好的泛化性能等優點[14-16]。

1)輸入層

CNN的輸入層用于接收輸入數據，其中1DCNN的輸入層的輸入參數為一維數據，在這里為發電機有功出力、發電機節點電壓、有功負荷和無功負荷組成的向量。

2)卷積層

卷積層的功能是對輸入數據進行特征提取，內部包含多個卷積核，并且含有權重和偏置需要進行訓練更新。卷積核比輸入參數維度小，對于1DCNN，卷積核也為一維，并且會在輸入參數上進行滑動，對其范圍內參數進行特征提取和映射，并且需要設置每次滑動步長。

3)激活函數

對卷積層得到的特征進行非線性化處理，增加模型的擬合能力，常用的激活函數有ReLU、Sigmoid等。

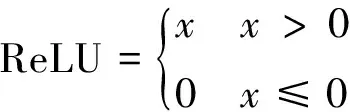
(4)

(5)

式中，x為激活函數的輸入。

所選用的激活函數為ReLU函數，如圖1所示。

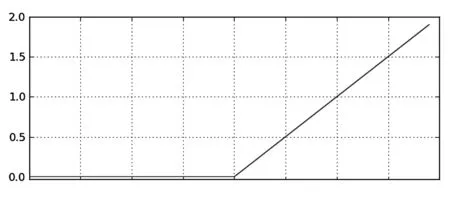
圖1 RuLU函數

4)池化層

池化層的作用是對數據進行降維，其會設定池化區域，在該區域內進行降維，常用的池化操作有：

(1)最大值池化：在池化區域內取最大值作為最終的特征。

(2)平均值池化：在池化區域內取均值作為最終的特征。

設滑動步長為2，卷積核長度為4，對長度為9的向量卷積結果如圖2所示。

圖2 最大值池化和平均值池化

5)全連接層

CNN中的全連接層等價于傳統前饋神經網絡中的隱含層，包括前向傳播和反向傳播兩部分。

前向傳播中，數據從輸入到輸出，第l層的輸出為

al=σ(zl)=σ(Wlal-1+bl)

(6)

式中：σ為激活函數；Wl為權重，bl為偏置；zl為未激活前輸出；al為輸出。

反向傳播由輸出向輸入傳播，并逐層更新權重和偏置，更新的依據為1DCNN的正向輸出結果和時域仿真計算結果的偏差，偏差的表達式為

(7)

式中：x為樣本輸入；y為樣本真值；J為偏差。

J對W和b求梯度為：

得到梯度后，使用隨機梯度下降法更新W和b，減小偏差。

6)輸出層

輸出層為CNN的最終輸出結果，1DCNN的最終輸出結果為所有故障的最大功角差。

除此之外，在訓練1DCNN的過程中使用了L2正則化仿真過擬合：

(10)

式中，λ為L2正則化的超參數。

1DCNN在Tensorflow框架上進行搭建，搭建好的1DCNN的模型如圖3所示。

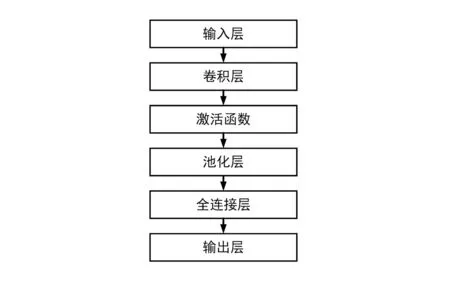
圖3 1DCNN結果

2.2 基于1DCNN的暫態穩定評估

1DCNN模型搭建好之后，將MCMC產生的運行場景(發電機有功出力、發電機節點電壓、有功負荷和無功負荷)作為1DCNN的輸入參數，將所有故障的最大功角差作為輸出參數，并對1DCNN進行訓練，所提1DCNN結構如圖4所示。

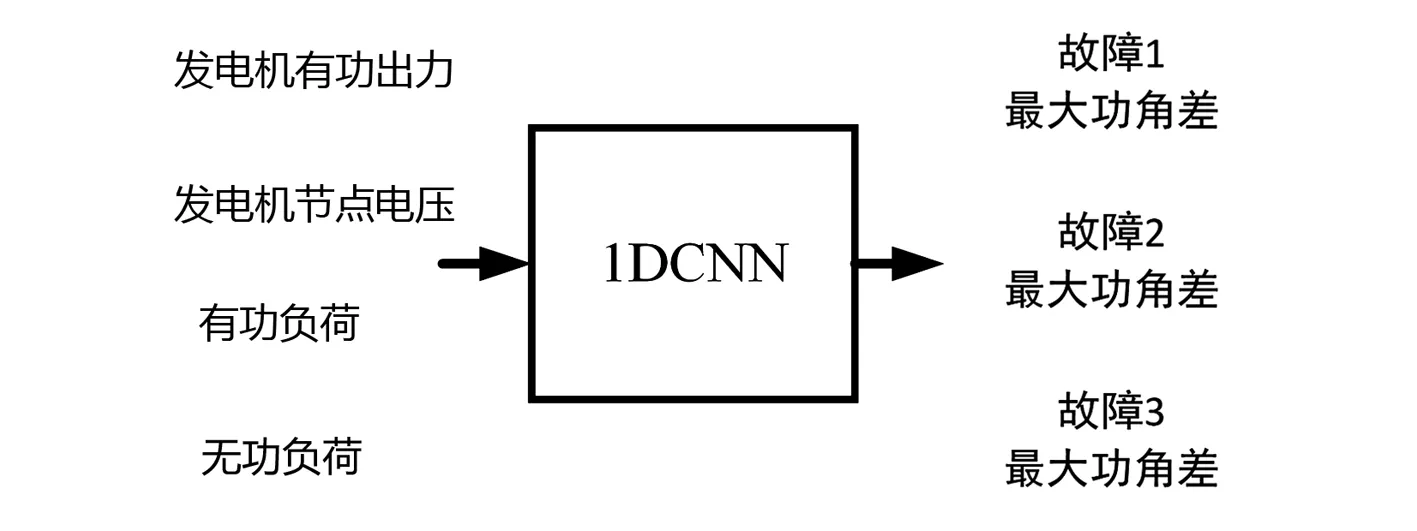
圖4 1DCNN結構

以發電機最大功角差是否超過180°作為判斷系統是否失穩的標準，并且只要有一個故障下的最大功角差超過180°，即認為系統失穩。因此準確度定義為1DCNN模型成功判斷系統穩定性的百分比。

3 算例分析

3.1 測試系統

選取新英格蘭10機39節點系統進行算例測試，該系統包括39個節點、10臺火力發電機、34條輸電線路、12臺兩繞組變壓器和19個負荷，該系統的示意圖如圖5所示[17]。

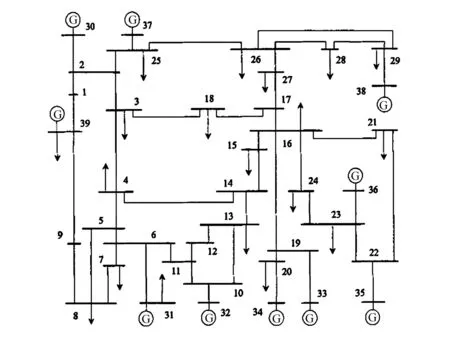
圖5 新英格蘭10機39節點系統

3.2 電力系統運行數據仿真

設置發電機有功出力在基礎出力的80%～120%、發電機節點電壓的標幺值在0.95～1.1、有功負荷和無功負荷均在80%～120%之間波動。通過MCMC算法抽樣5000個樣本，作為電力系統運行場景。

設置39節點系統的故障類型為輸電線路三相短路故障，故障位置為線路中心，故障數量為15條輸電線路，故障持續時間為0.5 s，在電力系統工具箱PST中進行時域仿真計算，得到不同故障下發電機的最大功角差，將其與對應的運行場景結合，作為訓練1DCNN的樣本數據。

3.3 基于1DCNN的暫態穩定評估結果

樣本數據生成后，對1DCNN模型進行訓練，將MCMC產生的運行場景(發電機有功出力、發電機節點電壓、有功負荷和無功負荷)作為1DCNN的輸入參數，輸入參數的維度為58；將所有故障的最大功角差作為輸出參數，輸出參數的維度為15。設置輸入層、卷積層、激活函數、池化層、全連接層和輸出層數量各為1，共6層。設置每批次訓練樣本數量為500，訓練次數為100，訓練集數量為4000，測試集數量為1000，對1DCNN進行訓練，其在訓練過程中的誤差曲線如圖6所示。

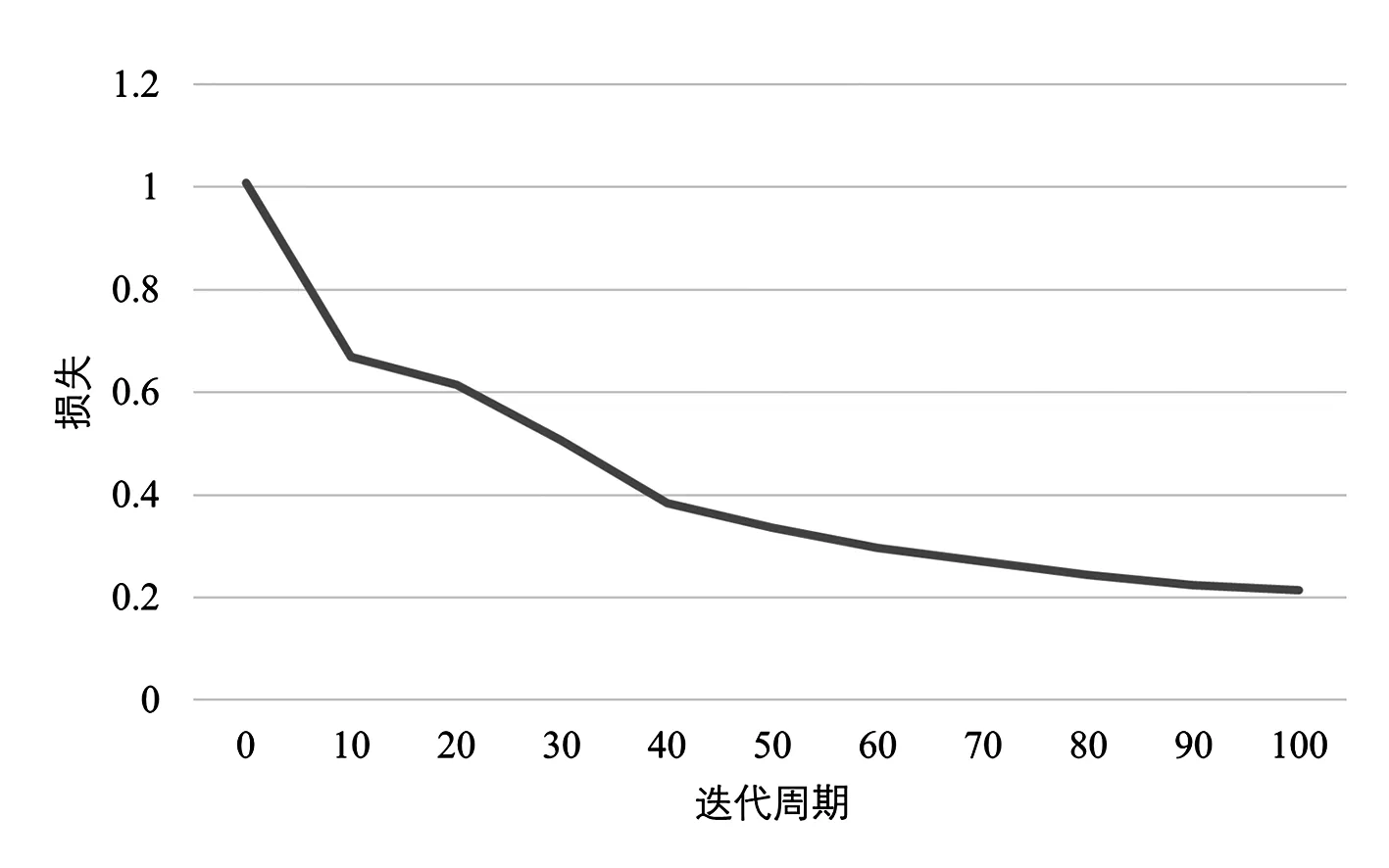
圖6 訓練集損失曲線

從圖6可以看出，隨著訓練迭代次數增加，損失逐漸降低，表明1DCNN實現了基于運行場景的暫態穩定擬合。

1DCNN的準確率如圖7所示。由圖7可以看出，隨著迭代周期的增加，1DCNN的準確度持續增加，并且在末端保持在90%以上的準確度，表明所提算法實現了暫態穩定的準確評估。

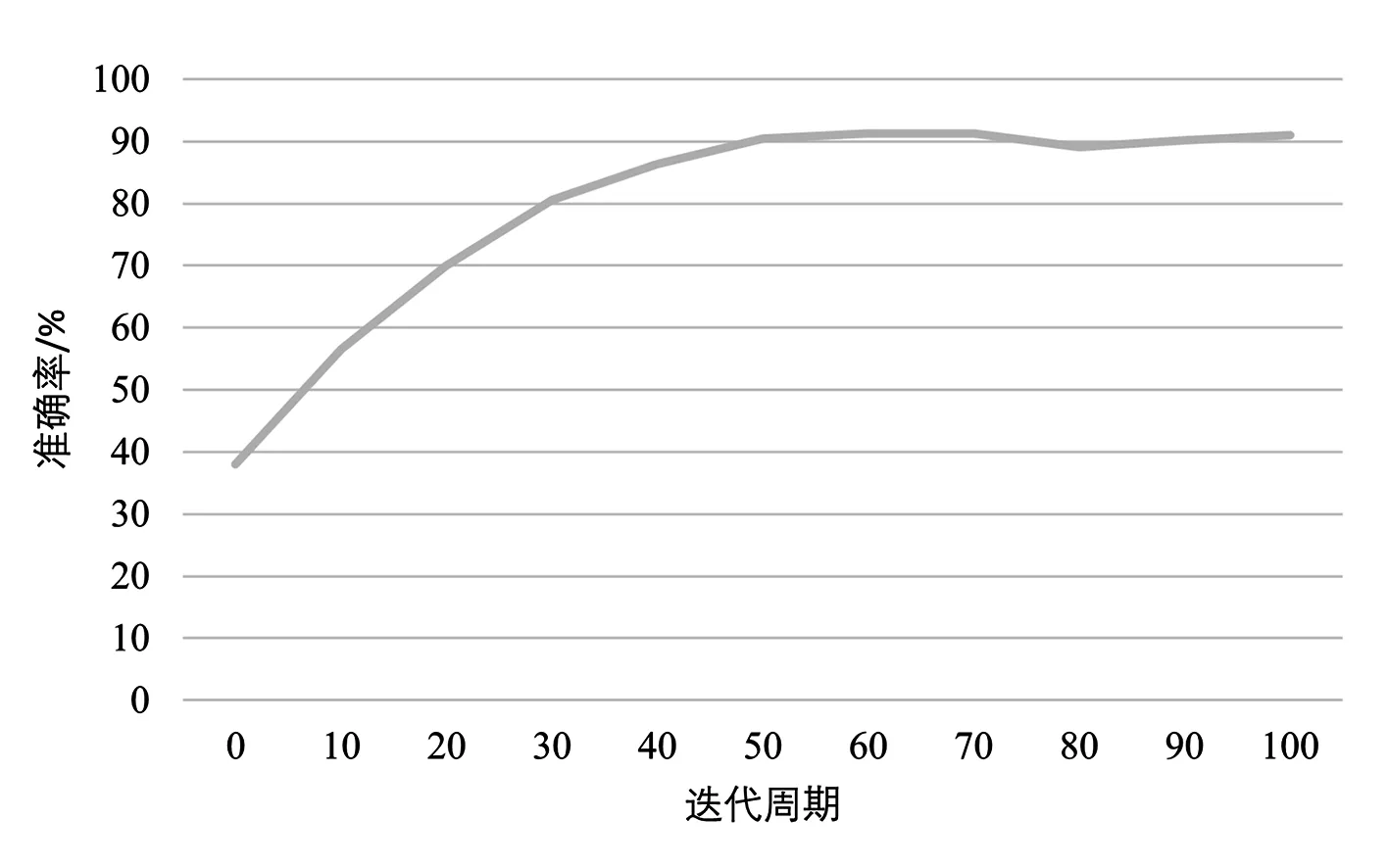
圖7 訓練集準確率曲線

訓練好1DCNN模型后，可進行在線的暫態穩定評估，與傳統基于時域仿真的暫態穩定評估相比，在評估速度上得到極大提升，評估時間對比如表1所示。

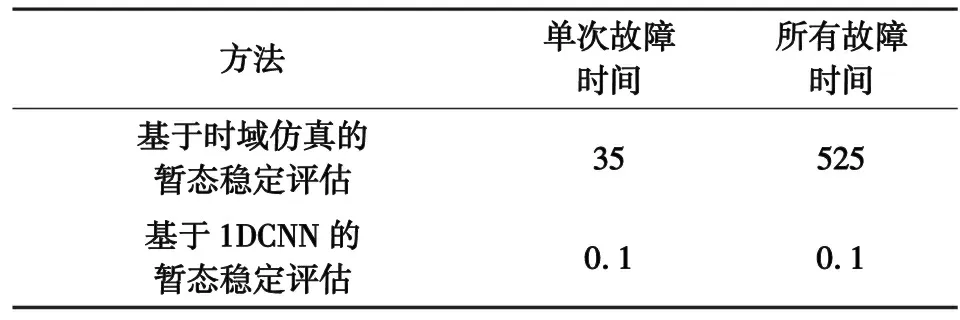
表1 算法評估時間對比單位：s

從表2可以看出基于1DCNN的暫態穩定評估算法在計算時間上相較于傳統時域仿真方法有極大提升，并且可以同時得到所有故障的暫態穩定評估結果，故障數量越多，算法在評估時間上的優勢越明顯。

最后，對比所提方法與其他文獻方法的評估準確度，結果如表2所示。

表2 評估準確度對比

從表2可以看出所提方法在準確度上明顯優于其他方法，可以實現更加精準的電力系統暫態穩定評估。

4 結 語

上面提出了一種基于1DCNN的電力系統暫態穩定在線評估算法。該算法將1DCNN引入電力系統暫態穩定評估和安全風險辨識中，通過MCMC算法生成算例模型海量可能的運行場景，并通過時域仿真計算暫態穩定指標，通過1DCNN實現暫態穩定性能快速評估。并在新英格蘭10機39節點系統中進行了算例驗證，算例結果表明了所提算法的可行性和先進性。通過算例分析，得到如下結論：

1)利用馬爾科夫鏈和蒙特卡洛抽樣算法結合的MCMC算法對電力系統運行場景進行抽樣，所生成樣本可以很好反映系統運行特征，提高1DCNN的泛化性能；

2)將1DCNN引入電力系統暫態穩定評估中，將系統運行場景作為輸入參數，將所有故障的最大功角差作為輸出，對1DCNN進行訓練，實現了基于1DCNN的電力系統暫態穩定快速評估，并且從算例結果可以看出所提算法評估時間滿足在線應用的需求。