SM2 密碼算法密鑰滲漏分析*
黃欣沂, 陳榮茂, 王 毅, 邢倩倩
1. 福建師范大學 計算機與網絡空間安全學院, 福州350117
2. 福建師范大學 福建省網絡安全與密碼技術重點實驗室, 福州350117
3. 國防科技大學 計算機學院, 長沙410073
1 引言
可證明安全理論為現代密碼學提供了嚴謹的安全性分析方法, 主要思想是基于計算復雜性理論, 將敵手攻擊密碼算法的過程與破解公認困難性數學問題建立近似等價聯系, 證明密碼算法的安全性. 可證明安全已被廣泛用于密碼算法的設計與安全性分析, 為促進密碼技術在現實生活中的應用提供了理論上的安全保障. 然而, 越來越多的安全事件表明, 理論上已被證明安全的密碼算法在實際應用中仍然可能失效. 這是因為可證明安全主要針對密碼算法的規范(specification) 進行理論分析, 而密碼算法在實際部署(implementation)應用時因為各種原因可能沒有嚴格遵守相應的規范,導致算法的安全性無法達到理論上已證明的安全級別, 甚至遭到徹底破壞.
2013 年著名的“斯諾登事件” 披露, 以美國國家安全局為代表的安全機構為了能夠對互聯網用戶實施大規模監聽, 控制密碼算法標準的制定, 篡改密碼產品中相關算法的軟硬件部署, 通過植入密碼后門獲取用戶私鑰, 破壞用戶的通訊隱私[1,2]. 因為密碼后門設計巧妙, 具有極強的隱蔽性, 所以直到“斯諾登事件”所披露的相關文檔公開之后才被公眾所知. “斯諾登事件” 在國際密碼學界迅速引起廣泛關注, 研究人員開始從技術層面研究美國政府大規模監聽背后的技術手段, 逐漸形成以研究密碼算法后門嵌入形式、工作原理和防范技術為核心的“后斯諾登密碼學”[3].
在2014 年的美密會上, Bellare 等提出“算法替代攻擊” (algorithm substitution attack, ASA)[4],用于刻畫對稱加密算法在實際部署時被篡改導致密鑰滲漏的一種特殊攻擊方法. 該種攻擊假設敵手可以控制加密算法的實際部署, 在算法中植入特定的后門, 使得算法在保持原有加密功能的情況下, 將用戶密鑰信息嵌入到可以正常解密的密文中. 攻擊者在捕獲到密文之后, 就可以利用后門信息從密文中分析還原用戶密鑰信息, 從而解密密文得到明文信息. 這種攻擊的雛形最早可以追溯到上世紀90 年代由Young 等提出的“盜碼學” (kleptography) 概念[5–7]. 該攻擊技術主要考慮在黑盒密碼體制中秘密嵌入后門(secretly embedded trapdoor with universal protection, SETUP) 破壞密碼算法安全性的情況. 與Bellare 等提出的ASA 攻擊不同, SETUP 攻擊主要考慮的是非對稱方式嵌入的后門, 即被嵌入后門與攻擊者還原密鑰所用的后門信息是公私鑰的關系. 從攻擊者的角度來講, 這種攻擊方式可以更好地保持攻擊專有性(exclusivity), 即使內嵌的后門信息被發現, 也無法攻擊其他被嵌入相同后門的密碼系統.
在Bellare 等的工作之后,國內外學者圍繞對稱加密[8,9]、數字簽名[10–12]、格上公鑰加密[13]、消息驗證碼[14]等不同密碼算法開展了深入的后門攻擊評估. 本文將在1.3 節對這些工作進行總結闡述. 雖然這些攻擊在具體的定義上不完全相同, 但都是通過篡改算法部署, 將密鑰信息嵌入算法的輸出中, 達到密鑰滲漏的目的. 因此, 為了后面敘述的一致性, 本文將這類攻擊統一稱之為“密鑰滲漏攻擊” (key exfiltration attack, KEA). KEA 也可以用于隱蔽傳輸其他秘密信息, 比如加密的明文和加密過程產生的隨機數等敏感信息. 這一點和以實現隱蔽傳輸為目標的隱寫術(steganography) 是類似的. 文獻[15] 已經從理論上嚴
謹論證了該種攻擊和傳統隱寫術之間存在近似等價的相互轉換關系, 即對于輸出具有一定最小熵值的加密算法, 存在和算法內部運行細節無關的通用后門攻擊.
1.1 研究動機
我國自主設計的國產商用密碼是實現信息系統安全可控的核心保障, 在使用過程中也將遭受一系列不同動機的安全分析和惡意攻擊. 由于國產商用密碼在設計之初沒有考慮密鑰滲漏攻擊, 目前也未見公開發表的針對國產商用密碼的密鑰滲漏攻擊分析(下面簡稱KEA), 所以本文重點評估國產商用密碼SM2 數字簽名算法和公鑰加密算法面臨的KEA 威脅, 并提出相應的防范技術. 雖然Bellare 等提出的“偏密文攻擊”(biased-ciphertext attack)[4]和Ateniese 等提出的“偏隨機數攻擊”(biased randomness attack)[10]具有通用性, 也同樣適用于SM2 算法, 但這些KEA 攻擊方式有兩個不足:
(1) 采取“逐比特滲漏” 方式進行密鑰滲漏. 該方式具有很強的通用性, 但滲漏效率比較低. 其核心思路是通過“拒絕采樣” (rejection sampling) 的方式生成隨機數, 直到算法的輸出滿足預設的條件(如在某個特定函數下表示某一比特密鑰信息).
(2) 采用“對稱方式” 植入后門密鑰, 即算法內嵌后門信息和攻擊者提取密鑰所用的后門信息相同. 該種形式后門簡單通用, 但某種程度上會弱化密鑰滲漏攻擊能力的專有性. 一旦用戶發現算法內嵌的后門信息, 就可以獲得和攻擊者同樣的攻擊能力.
因此, 本文旨在探索SM2 算法是否面臨比“逐比特滲漏” 方式更加高效且基于非對稱后門(和SETUP 類似[5–7]) 的密鑰滲漏攻擊威脅.
1.2 本文貢獻
針對上述問題, 本文首先給出適用于數字簽名算法和公鑰加密算法的KEA 模型, 主要刻畫KEA 攻擊的兩個性質: “攻擊不可檢測性” 和“密鑰可還原性”. 前者用于刻畫攻擊的隱蔽性, 即用戶通過觀察算法的輸入輸出無法辨別算法是否被篡改. 后者用于描述該種攻擊的危害性, 即攻擊者通過捕獲分析算法的輸出可以提取密鑰. 在給出攻擊模型的基礎上, 本文針對SM2 數字簽名算法和公鑰加密算法進行KEA 威脅評估, 具體結果如下:
(1) 提出針對SM2 數字簽名算法的對稱密鑰滲漏攻擊. 該攻擊使得攻擊者通過2 個連續的簽名就能提取簽名密鑰. 和Ateniese 等提出的“偏隨機數攻擊”[10]相比, 本文提出的攻擊將完整還原密鑰所需的簽名數量從與密鑰長度線性相關降低到常數.
(2) 提出針對SM2 公鑰加密算法的非對稱密鑰滲漏攻擊.與對稱加密算法不一樣,公鑰加密算法的運行沒有用戶私鑰的參與. 本文提出了一種能夠高效滲漏SM2 公鑰加密會話密鑰(session key) 的攻擊. 該攻擊使得攻擊者通過當前密文能夠成功預測下一次會話使用的加密密鑰, 從而具備解密能力.
此外, 本文還對現有相關的抗KEA 技術進行分類總結, 并結合SM2 數字簽名算法和公鑰加密算法的構造特點選取具有可行性的防范技術進行討論.
1.3 相關工作
目前國際密碼學界在后斯諾登密碼學領域取得了一定的進展, 主要體現在對一系列密碼算法的后門威脅評估和基于各種假設條件的防范方法設計兩個方面. 文獻[16] 已經做了比較全面的總結, 下面按照不同的密碼算法分類介紹與KEA 威脅評估相關的工作.
對稱加密算法: Bellare 等針對密文中包含IV 等公開隨機數的對稱加密算法, 在文獻[4] 中提出了IV-replacement attack. 主要思路是在算法輸出的密文中將包含用戶密鑰的密文作為IV 直接輸出, 因此比“偏密文攻擊” 更加高效. 隨后, Bellare 等[8]提出了一種改進的攻擊方法, 避免“偏密文攻擊” 需要維護內部狀態、記錄所滲漏密鑰比特位置信息的不足. 主要思路是通過采用特殊的評估函數, 不僅可以根據每次密文提取密鑰比特信息, 還可以獲取該比特所在的位置信息. 該種攻擊由于采用coupon collection 的原理,因此比“逐比特滲漏”的效率更低. Degabriele 等[9]提出了“輸入觸發攻擊”(input-trigger attack).該種攻擊只有在加密算法接收到特定輸入信息的時候才會被觸發, 而且可以直接將密鑰輸出, 因此效率很高.
數字簽名算法: Ateniese 等[10]則針對簽名體制開展了KEA 探索, 提出了兩種攻擊方式: “隨機數可提取攻擊” (coin-extractable attack) 和“偏隨機數攻擊” (biased randomness attack). 前種攻擊與Bellare 等提出的IV-replacement attack 類似, 主要是將滲漏密鑰的密文作為算法輸出中的公開隨機數,第二種攻擊則和“偏密文攻擊” 類似, 也是通過“拒絕采樣” 的方式, 產生特定的合法簽名輸出. Teseleanu等[11]針對基于離散對數困難性假設的數字簽名方案提出了門限SETUP 攻擊方式. 柳馳等在文獻[12]中針對“可分割數字簽名方案” 提出了一種高效的KEA. 該攻擊方式類似于SETUP 攻擊, 采用非對稱方式在算法中嵌入后門, 且僅需要2 個連續簽名就能滲漏整個密鑰.
公鑰加密算法: 陳榮茂等[17]對采用混合式加密(hybrid encryption) 的公鑰加密方案進行了嚴謹的論證分析, 發現現有大部分采用該結構的公鑰加密方案面臨一種非常高效的加密會話密鑰滲漏攻擊. 攻擊者通過上一個密文能夠成功預測下一個會話中的加密密鑰. 事實上, 文中針對公鑰加密方案的密鑰滲漏攻擊可以看做是陳榮茂等攻擊框架在SM2 公鑰加密方案下的一種實例化, 因此進一步證實了該種攻擊的廣泛存在性. 在具體方案攻擊方面, 楊智超等[13]針對格上公鑰加密方案提出了具體的KEA 攻擊. Russell等在[18] 中也針對公鑰加密方案提出了一種通用的攻擊, 其主要思路是采用Bellare 等[4]提出的“偏密文攻擊” 方法.
其他密碼算法: 除了上述主流的密碼體制, Armour 等[14]也分析了MAC 所面臨的密鑰滲漏威脅.呂佳憲等[19]則對云數據審計協議中挑戰因子的可信問題進行研究, 提出了一種通過挑戰信息滲漏簽名密鑰的具體攻擊. 此外, 還有一些工作[20,21]針對密碼算法的參數安全問題進行了研究.
1.4 本文結構
本文組織結構如下: 第2 節介紹相關預備知識. 第3 節形式化定義針對數字簽名方案和公鑰加密方案的KEA 模型. 第4 節提出針對SM2 數字簽名算法的具體KEA 攻擊以及形式化分析. 第5 節提出針對SM2 公鑰加密算法的具體KEA 攻擊以及形式化分析. 第6 節討論適用于SM2 密碼算法的抗KEA 技術.
2 預備知識
本節介紹后續章節使用的主要符號表示和涉及的密碼基礎概念.
2.1 符號表示
對于任意非空集合X,x ←$X表示從X中隨機選取元素x. 對于任意隨機算法F(·),y ←$F(x)表示算法F的隨機輸出. poly(n) 表示n的多項式函數; 如果某n的函數比n的任何多項式函數的倒數衰減得更快, 則稱其為可忽略函數, 使用negl(n) 表示. 如果對于任何長度為n的輸入, 算法A最多在poly(n) 步內結束, 則稱A為概率多項式時間(PPT) 算法. 對于任意整數i,j滿足i 定義1 (計算性Diffie-Hellman (CDH) 困難性假設) 令正整數n為安全參數, G 為一個階為素數p的群,g為群G 的生成元. 計算性Diffie-Hellman 困難性假設指的是對于所有的PPT 算法A, 定義2 (熵平滑的密碼雜湊函數簇) 令正整數n為安全參數,F={Fκ}κ∈K表示一個具有密鑰的密碼雜湊函數簇, 其中K為密鑰空間. 假設該函數簇中的每個密碼雜湊函數Fκ將群G 中的元素映射到集合{0,1}?中. 我們稱該函數簇是熵平滑的, 當且僅當對于所有的PPT 算法D, 數字簽名方案主要由4 個算法組成: 分別是初始化算法、密鑰生成算法、簽名算法和驗證算法. ? 初始化算法Setup: 輸入安全參數1n, 輸出系統參數pp; ? 密鑰生成算法KGen: 輸入系統參數pp, 輸出簽名私鑰sk 和驗證公鑰vk; ? 簽名算法Sign: 輸入簽名私鑰sk 和消息M, 輸出簽名σ; ? 驗證算法Vrfy: 輸入驗證公鑰vk, 消息M和簽名σ, 若σ是M的合法簽名, 輸出1; 否則輸出0. 簡潔起見, 本文將系統參數pp 從簽名算法Sign 和驗簽算法Vrfy 的輸入中省略. 令M為消息空間, 數字簽名方案的正確性要求對于任意的系統參數pp←$Setup(1n), 任意的簽名私鑰和驗證公鑰(vk,sk)←$KGen(pp) 和任意消息M ∈M, 公鑰加密方案主要由4 個算法組成: 分別是初始化算法、密鑰生成算法、加密算法和解密算法. ? 初始化算法Setup: 輸入安全參數1n, 輸出系統參數pp; ? 密鑰生成算法KGen: 輸入系統參數pp, 輸出公私鑰對(pk,sk); ? 加密算法Enc: 輸入公鑰pk 和明文M, 輸出密文C; ? 解密算法Dec: 輸入私鑰sk 和密文C, 輸出明文M或者特殊符號⊥. 簡潔起見, 本文將系統參數pp 從加密算法Enc 和解密算法Dec 的輸入中省略. 令M為明文空間, 公鑰加密方案的正確性要求對于任意的系統參數pp←$Setup(1n), 任意的公私鑰對(pk,sk)←$KGen(pp) 和任意的明文M ∈M, 本節將分別介紹針對數字簽名算法和公鑰加密算法的KEA 模型及其性質. ? 初始化階段: 運行Setup(1n) 生成系統參數pp, 運行KGen(pp) 生成簽名私鑰sk 和驗證公鑰vk,運行SKGen(pp) 生成后門密鑰ssk, 并將(pp,sk,vk) 發送給檢測者D; ? 挑戰階段: 隨機選取b ←${0,1}. 令SignProc(·) 為如下簽名詢問應答機, 假設詢問輸入為消息M: 檢測者D向SignProc(·) 發起q(n) 次詢問, 其中q(n) 為關于n的任意多項式; ? 猜測階段: 在詢問階段結束后, 檢測者D輸出b′. 當b=b′時, 該游戲輸出1, 否則輸出0. 本節將首先對SM2 數字簽名方案進行簡要介紹, 然后給出針對SM2 數字簽名算法的具體KEA 方案, 最后證明該KEA 具有不可檢測性和簽名私鑰可還原性. SM2 數字簽名方案的系統參數pp 包括: 有限域Fq, 橢圓曲線E(Fq) 及該曲線上的無窮遠點O, 任意選取的基點G= (xG,yG)(G ?=O), 基點G的階n及其余因子h, 消息摘要長度為v比特的密碼雜湊函數Hv, 部分橢圓曲線系統參數. 假設系統參數pp 還包括用戶A的可辨別標識, 和用戶A公鑰的雜湊值為ZA. SM2 數字簽名方案中的密鑰生成算法、簽名算法和驗證算法分別如算法1—算法3 所示. 算法1 SM2 簽名密鑰生成算法Input: 系統參數pp Output: 簽名私鑰及驗證公鑰對(sk,vk)1 dA ←$ [1,n ?1]2 PA = [dA]G 3 (sk,vk) = (dA,PA)4 return (sk,vk)算法2 SM2 簽名算法Input: 系統參數pp, 簽名私鑰dA, 消息M Output: 簽名σ 1 ^M = ZA||M 2 e = Hv(^M)3 k ←$ [1,n ?1]4 (x1,y1) = [k]G 5 r = (e+x1) mod n 6 s = ((1+dA)?1 ·(k ?r·dA)) mod n 7 σ = (r,s)8 return σ 算法3 SM2 驗證算法Input: 系統參數pp, 驗證公鑰dA, 消息M′,簽名σ′Output: 1 或0 1 (r′,s′) = σ′2 if r′ /∈[1,n ?1]∨s′ /∈[1,n ?1] then 3 return 0 4 end 5 ^M′ = ZA||M′6 e′ = Hv(^M′)7 t = (r′ +s′) mod n 8 (x′1,y′1) = [s′]G+[t]PA 9 R = (e′ +x′1) mod n 10 if R ?= r′ then 11 return 0 12 end 13 return 1 在進行攻擊前, 攻擊者需要運行算法SKGen 生成后門密鑰ssk: 攻擊者首先從G 中隨機選取生成元PS, 然后從密碼雜湊函數簇F={Fκ}κ∈K中隨機選擇密碼雜湊函數Fκ:G→[1,n ?1], 其中G 為橢圓曲線E(Fq) 上所有點的集合. 因此, ssk=(PS,Fκ). 根據引理1,G0和G1對于任意PPT 算法而言不可區分. 綜上所述, 上述攻擊是不可檢測的.定理2 上述攻擊是簽名私鑰可還原的. 根據上述步驟, 攻擊者A可以還原出簽名私鑰. 本節將首先簡要介紹SM2 公鑰加密方案, 然后給出針對SM2 公鑰加密算法的具體KEA 方案, 最后證明該KEA 具有不可檢測性和明文可還原性. SM2 公鑰加密方案的系統參數pp 包括: 有限域Fq, 橢圓曲線E(Fq) 及該曲線上的無窮遠點O, 任意選取的基點G= (xG,yG)(G ?=O), 基點G的階n及其余因子h, 密鑰派生函數KDF 和密碼雜湊函數H, 其中密鑰派生函數KDF 輸入比特串Z和整數?, 輸出長度為?的密鑰數據比特串K. 和數字簽名方案的密鑰生成算法類似, SM2 公鑰加密方案的密鑰生成算法首先從[1,n ?1] 中隨機選取一個整數dB作為私鑰, 然后計算公鑰PB= [dB]G. SM2 公鑰加密方案中的加密算法和解密算法分別如算法4 和算法5 所示. 算法4 SM2 加密算法Input: 系統參數pp, 公鑰PB, 明文M Output: 密文C 1 k ←$ [1,n ?1]2 C1 = [k]G 3 S = [h]PB 4 if S = O then 5 return ⊥6 end 7 (x2,y2) = [k]PB 8 klen = |M|9 t = KDF(x2||y2,klen)10 C2 = M ⊕t 11 C3 = H(x2||M||y2)12 C = C1||C2||C3 13 return C 算法5 SM2 解密算法Input: 系統參數pp, 私鑰dB, 密文C Output: 明文M 或特殊符號⊥1 S = [h]C1 2 if S = O then 3 return ⊥4 end 5 (x2,y2) = [dB]C1 6 klen = |C2|7 t = KDF(x2||y2,klen)8 M = C2 ⊕t 9 u = H(x2||M′||y2)10 if u ?= C3 then 11 return ⊥12 end 13 return M 下面形式化分析該攻擊具備不可檢測性和簽名私鑰可還原性. 定理3 在隨機預言機模型下, 令q(n) 為檢測者D發起EncProc 詢問的次數,q′(n) 為檢測者D發起H′詢問的次數, 若任意PPT 算法解決計算性Diffie-Hellman 問題的優勢為θ(n), 那么上述攻擊是(q(n)?1)·q′(n)·θ(n)-不可檢測的. 證明: 我們將通過設計一系列游戲來證明上述非對稱攻擊的不可檢測性. 令Ei表示事件b=b′在游戲Gi中發生. ? 游戲G3與游戲G2相同, 除了在游戲G3中加密詢問應答機EncProc(·) 的實現與游戲G2中的略有不同. 具體來說, 游戲G3中的加密詢問應答機EncProc(·) 在b= 1 時也輸出C ←$Enc(pk,M). 顯然, 此時在游戲G3中Pr[E3]=1/2. 綜上所述,?(n)≤(q(n)?1)·q′(n)·θ(n). 該定理成立.定理4 上述攻擊是明文可還原的. 根據上述攻擊的描述, 攻擊者A可以還原出除密文C1以外的所有密文的明文. 由于KEA 具有很強的破壞性且不在傳統安全性分析的考慮范疇, 因此需要研究設計新的技術手段來抵御這種攻擊. 目前學術界已有若干研究工作嘗試提出具備一定可行性的防范技術. 本文將介紹部分具有代表性的研究工作, 并結合SM2 密碼算法方案進行討論. 更具體詳細的總結可以參考國內學者李耕等的綜述工作[16]. 現有提出的KEA 雖然在具體實施細節上各有不同, 但本質上都是因為密碼算法輸出的不確定性所造成的. 由于密碼算法輸出的不確定性與其運行時臨時生成的隨機數直接相關, 因此有一部分學者建議采用不依賴于隨機數的密碼機制[4,9,10,22]來抵抗KEA. 特別地, Bellare 等[4]提出了具備唯一密文(unique ciphertext) 性質的對稱加密算法, 即給定一個明文, 加密算法所輸出的合法密文只有一個. 類似的, Ateniese 等[10]提出了具備唯一簽名(unique signature) 性質的數字簽名算法. 文獻[4,10] 通過形式化分析證明, 在KEA 具備不可檢測性的情況下, 上述類型的密碼算法可以實現抵抗KEA 的安全性. 上述方法具備一定的可行性. 然而隨機數是密碼算法常規情況下實現特定安全性(如選擇明文攻擊不可區分性) 的必備條件. 因此放棄隨機數的使用從實現密碼算法安全性的角度來講不是一種很理想的選擇.針對這個問題, 另外一些學者嘗試在使用隨機數情況下設計抵抗密鑰滲漏攻擊的可行技術. 然而文獻[15]從理論上證明了所有隨機化算法均面臨KEA 威脅, 因此需要基于新的假設性條件(如可信第三方), 否則無法實現抗KEA 安全性. 需要指出的是, 由于假設條件的不同, 現有提出的防范技術之間不具備可比性.下面我們將根據假設條件分類闡述, 并結合SM2 密碼算法進行討論. 密碼逆向防火墻技術是Mironov 等[23]在2015 年首次提出的概念. 類似于傳統的網絡防火墻, 逆向防火墻部署在密碼算法所運行機器的網絡邊界, 負責對被保護算法所有發送和收到的消息進行處理從而實現抵抗KEA 的目的. 實際上, 密碼逆向防火墻可以看做是一段運行在可信機器上的重隨機化算法代碼, 其工作的主要原理是在不破壞協議功能性的情況下重隨機化算法所輸出的消息, 從而消除被篡改密碼算法在其輸出消息中所嵌入的密鑰比特信息. 密碼逆向防火墻技術已被證明可以用于實現很強的抗KEA 安全性, 在某些特定的情況下甚至可以防范任意的密鑰滲漏攻擊行為, 因此得到了若干工作[10,24–27]的進一步拓展研究. 然而該技術要求被保護密碼算法具備可重隨機化的性質, 因此無法直接適用于不具備這種性質的SM2 密碼算法. 一個具有潛在可行性的解決思路是弱化對于密碼逆向防火墻透明性的要求, 使其與終端機器進行交互獲得輔助信息, 從而具備重隨機化簽名和密文的能力, 但如何降低密碼逆向防火墻對原有算法安全性的影響是需要考慮的主要問題. Russell 等[18]從體系結構設計的角度提出了程序分割(split-program) 模型. 該模型假設密碼算法由若干個獨立的模塊構成. 而這些模塊在實際部署的時候會由一個擁有各個模塊對應標準規范(specification) 的可信“監視犬” (watchdog) 逐個進行比對檢測. 只有通過檢測的模塊才能被組裝成完整的密碼算法投入使用. 基于這種模塊化設計思想, 文獻[18] 從理論上證明, 通過watchdog 檢測模塊所組裝成的密碼算法可以實現抗KEA 安全性. 其核心思路是將密碼算法分成確定性模塊和隨機數生成模塊. 前者可以通過比對檢測保證與相關規范的一致性, 而后者通過特殊的構造可以生成可信的隨機數. 這種“分割-融合” (decomposition and amalgamation) 的思想具有較強的通用性, 已被應用于構造隨機數生成器[18]、數字簽名算法[18,28]、公鑰加密方案[29,30]以及隨機預言機[31]等. 由于SM2 數字簽名算法和公鑰加密算法是隨機化算法, 因此上述技術同樣適用. Fischlin 等[32]提出了基于“自我防護” (self-guarding) 思想的密碼算法構造技術. 其假設密碼算法部署在某個時期(如早期階段) 沒有遭到篡改. 在這種假設條件下, 通過收集該階段算法執行所產生的消息流, 并用這些“干凈” 的樣本對后期可能被攻擊的密碼算法輸出進行修改, 可以實現抵抗KEA 的安全性.該技術和密碼逆向防火墻的本質思想是一樣的, 都是依賴可信的隨機數對可能內嵌密鑰信息的算法輸出進行處理從而抵抗KEA. 不同的是, 該技術不需要依賴可信的第三方而需要假設算法存在沒有被攻擊的階段. 自我防護技術可以作為解決密碼逆向防火墻無法適用不具備可重隨機化性質密碼算法時的一種可行思路. 不足的地方是, 這種技術需要修改原有密碼方案的設計, 而且只能防范某個時間段發起的密鑰滲漏攻擊類型(如時間炸彈攻擊), 并依賴于算法安全階段所收集的樣本數量. 文獻[32] 分別給出了抗KEA 的公鑰加密、對稱加密和數字簽名方案構造. 其中數字簽名算法的構造同樣適用于SM2 數字簽名. 而公鑰加密算法構造由于要求具有同態性質, 因此并不直接適用于SM2 公鑰加密方案. 針對密碼算法開展密鑰滲漏攻擊評估是“后斯諾登密碼學” 領域的重要研究問題之一. 本文定義了評估密鑰滲漏攻擊的兩個性質: 不可檢測性和密鑰/明文可還原性. 在此基礎上, 針對國產商用密碼SM2 數字簽名算法和公鑰加密算法, 分別提出兩種高效的密鑰滲漏攻擊. 通過理論分析, 證明提出的密鑰滲漏攻擊滿足上述兩個性質. 本文的研究結果表明, SM2 數字簽名算法和公鑰加密算法面臨的密鑰滲漏攻擊威脅比已知的通用攻擊更加嚴重, 在實際部署時應采取相應的防范技術. 需要指出的是, 我們暫時還沒有發現針對SM2 數字簽名算法的具有非對稱形式的密鑰滲漏攻擊. 柳馳等的工作[12]實現的非對稱方式的密鑰滲透攻擊僅針對特定的數字簽名類型, 即“可分割數字簽名方案”. 而SM2 數字簽名算法并不屬于這一類別, 因此無法將現有攻擊方式應用到該簽名算法. 本文提出的高效密鑰滲漏攻擊并不能適用于SM2 密碼算法中的密鑰交換協議. 主要原因是SM2 密鑰交換協議采用單輪交互, 協議雙方在執行過程中只交換臨時隨機數, 并沒有公開傳輸與用戶私鑰相關的信息. 因此, 雖然本文提出的攻擊方法可以完整滲漏雙方密鑰協商時所生成的內部隨機數, 卻無法用于高效還原用戶私鑰. 此外, 由于雙方協商的會話密鑰由用戶私鑰和臨時隨機數共同決定, 因此攻擊者在只獲得隨機數的情況下也仍然無法還原會話密鑰.2.2 困難性問題
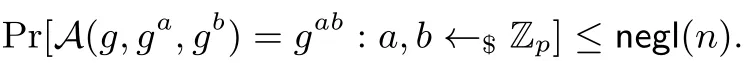
2.3 密碼雜湊函數
2.4 數字簽名方案
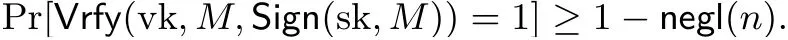
2.5 公鑰加密方案
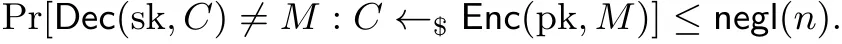
3 密鑰滲漏攻擊模型
3.1 數字簽名算法KEA 模型






3.2 公鑰加密算法KEA 模型


4 針對SM2 數字簽名算法的對稱密鑰滲漏攻擊
4.1 SM2 數字簽名方案


4.2 具體KEA 方案及理論分析

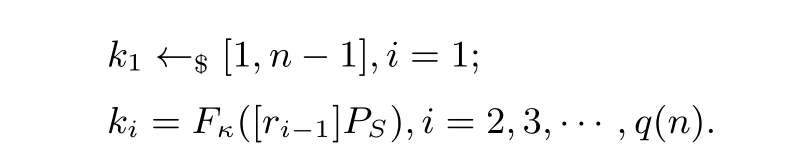



5 針對SM2 公鑰加密算法的非對稱密鑰滲漏攻擊
5.1 SM2 公鑰加密方案


5.2 具體KEA 方案及理論分析






6 抗密鑰滲漏攻擊技術討論
6.1 密碼逆向防火墻技術
6.2 基于監視犬的防范技術
6.3 自我防護技術
7 總結

