GNSS-R 信噪比信號在海面測高技術(shù)的研究綜述

胡媛，鐘李程，陳行楊，顧旺旺，劉衛(wèi)

( 1.上海海洋大學(xué)工程學(xué)院上海， 201306；2.上海海事大學(xué)商船學(xué)院上海， 200135)

0 引言

近年來，全球氣候變暖，兩極冰川融化導(dǎo)致海平面的上升.隨著海平面的上升，海拔低的沿海地帶將被淹沒，數(shù)百萬居民流離失所.此外，風(fēng)暴、極端海浪和颶風(fēng)等自然災(zāi)害頻繁發(fā)生，因此，監(jiān)控海平面的變化對于沿海人民的生活有著重大的意義.傳統(tǒng)監(jiān)測海平面的方法是通過岸邊驗潮儀進行監(jiān)測，但是傳統(tǒng)驗潮儀測量的是相對海面高度，其測量結(jié)果是絕對海面和地殼垂直方向的形變共同組成的相對海面高度.測量絕對海面高度則需要通過全球衛(wèi)星導(dǎo)航系統(tǒng)(GNSS)抵消地殼垂直位移的影響，并且傳統(tǒng)驗潮儀在風(fēng)浪的作用下，測量儀器可能會出現(xiàn)零點漂移現(xiàn)象[1].

自Hall 等[2]提出全球衛(wèi)星導(dǎo)航反射信號(GNSS-R)的概念以來，GNSS-R 被廣泛應(yīng)用于遙感方面.如土壤濕度檢測[3-8]、降雪深度檢測[9-13]、海冰檢測[14-17]、海面溢油檢測[18-21]，同樣GNSS-R 也被運用于監(jiān)測海平面.1993年，Martin-Neira[22]首次提出被動反射和干涉測量系統(tǒng)，即PARIS(passive reflectometry and interferometry system)的概念，PARIS的主要理論思想是利用從海面反射過來的GPS信號測量海面高度，并且同時測量多個反射點，利用多個衛(wèi)星信號來達到很高的測量精度.

自PARIS概念提出，許多研究人員在GNSS-R海面測高方面做了大量的研究.目前為止，利用GPS信號測量海面高度可以大致分為兩類，相位差分析[23]和信噪比(SNR)分析[24].相位差分析是使用兩根天線來確定直射信號和來自海面的反射信號之間的相位差，包括碼相位差法和載波相位差法[25]，從而得出兩個信號的路徑差來確定海面高度.其中直射信號為右圓極化(RHCP)信號，反射信號的極化特性通常情況下從RHCP轉(zhuǎn)變?yōu)樽髨A極化(LHCP)，這種改變由反射面的介電特性和發(fā)射機-反射面-接收機的幾何結(jié)構(gòu)決定[26].該技術(shù)需要運用雙天線的接收機，這種接收機結(jié)構(gòu)復(fù)雜，成本大并且需要專業(yè)人員安裝.SNR 分析方法利用單根天線接收直射信號和反射信號所產(chǎn)生的干涉模式技術(shù)(IPT)[25]，利用所獲得的SNR 與衛(wèi)星仰角的函數(shù)關(guān)系來確定海面高度.運用SNR 數(shù)據(jù)分析只需要單根天線來測量海面高度，并且對風(fēng)浪條件具有更好的魯棒性.但是目前該方法的測量精度還不如利用相位差測量方法的精度高，所以許多研究者正在研究運用SNR 數(shù)據(jù)提高測量精度的算法.本文圍繞SNR 數(shù)據(jù)測量海面高度中運用的算法進行展開，介紹在利用SNR 數(shù)據(jù)反演海面高度所運用的算法，為以后運用SNR 數(shù)據(jù)進行海面測高提供一些參考.

1 基于SNR 測高的基本原理

1.1 GNSS-R 測高原理

利用GNSS-R 進行海面測高的基本模型如圖1所示，接收機接收來自衛(wèi)星的直射信號和經(jīng)海平面反射的反射信號.因為接收機與衛(wèi)星之間的距離足夠遠，所以可以認為直射信號和反射信號為平行關(guān)系.由圖1所示的幾何關(guān)系，可以得到

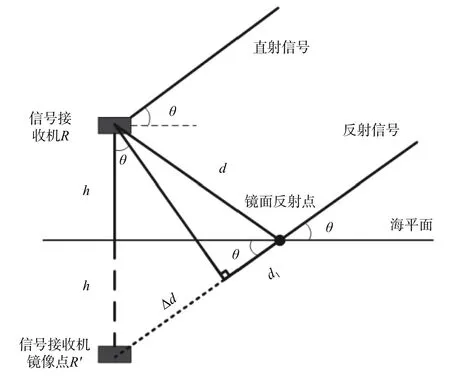
圖1 GNSS-R 海面測高幾何關(guān)系圖

式中：Δd為直射信號與反射信號的路程差；h為接收機到海面的垂直高度；θ為衛(wèi)星仰角.

1.2 SNR 信號的數(shù)據(jù)特點

因為利用SNR 測量海面高度只用了一根天線，所以接收機的信號為反射信號和直射信號發(fā)生干涉而形成.根據(jù)文獻[27]可知，SNR 與接收機之間存在以下關(guān)系：

由式(5)中可知，基于SNR 數(shù)據(jù)反演海面高度，只需要求解出去除趨勢項后的SNR 數(shù)據(jù)的頻率.所以尋求合適的算法去除SNR 信號的趨勢項和提取去除趨勢項后的SNR 信號的頻率是利用SNR 信號反演海面高度的關(guān)鍵步驟.去除趨勢項和提取頻率對反演的海面高度精度起著至關(guān)重要的作用.

2 基于SNR 信號的測高方法

2.1 最小二乘法在反演海面高度的應(yīng)用

2.1.1運用最小二乘法去除趨勢項

最小二乘法是一種被廣泛應(yīng)用于消除趨勢項的方法[28].如式(2)所示，SNR 數(shù)據(jù)具有一個二階多項式的趨勢項，SNR 信號的采樣數(shù)據(jù)為{xk}(k=1,2,3,···,n).設(shè)趨勢項多項式函數(shù)

從而得到趨勢項多項式的系數(shù)，得出趨勢項擬合曲線，再用原始的SNR 數(shù)據(jù)減去得到的趨勢項，達到去除趨勢項的目的，結(jié)果如圖2所示.

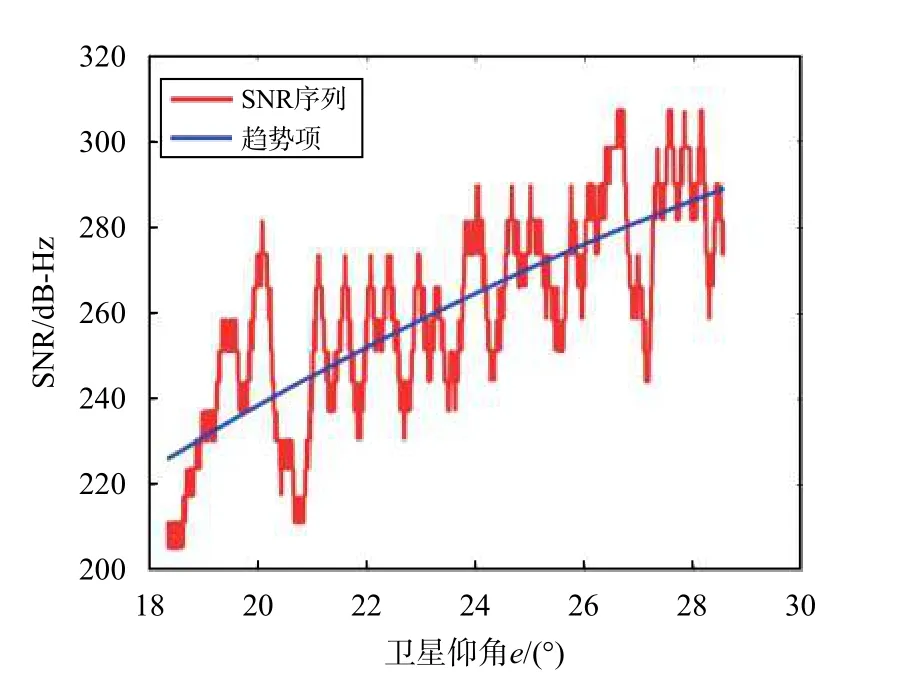
圖2 SNR 信號和擬合的趨勢項

2.1.2非線性最小二乘法擬合SNR 信號

通過非線性最小二乘法擬合得到的頻率即為去勢后信噪比數(shù)據(jù)的頻率，根據(jù)式(5)便可以反演出海面高度.

李惟等使用法國圖盧茲大學(xué)CESBIO實驗室的實測數(shù)據(jù)對上述方法進行驗證，同時與LSP方法進行對比.具體結(jié)果如表1所示.

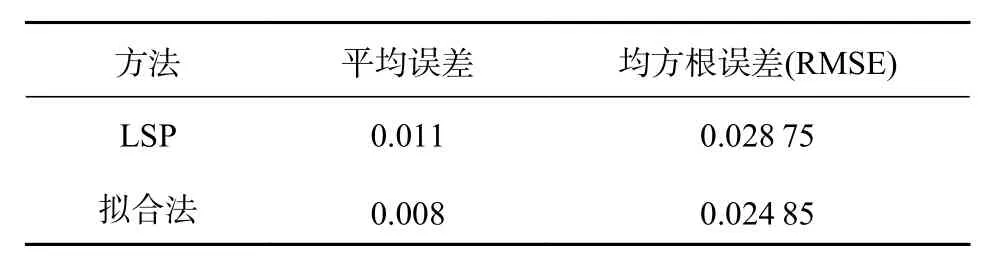
表1 LSP 法和擬合法反演結(jié)果m

2.2 LSP在反演海面高度的應(yīng)用

SNR 信號在時間上是均勻采樣的，但是實際接收機接收的SNR 信號因變量是衛(wèi)星仰角的正弦值，這導(dǎo)致SNR 信號是非均勻分布的，并且接收信號時存在噪聲干擾.在運用傅里葉變換時，這些噪聲和不均勻分布會對頻譜分析產(chǎn)生影響，造成頻譜圖與SNR 信號實際結(jié)果偏差很大.Larson K M 等[24]提出運用Lomb標準化周期圖(LSP)方法對SNR 進行分析，獲取該信號的頻率.

LSP是由Lomb[31]于1976年提出，并在1986年由Scargle[32]進行修改完善，LSP有sin 和cos兩組基，并且在時域方面做了歸一化的處理.因此，LSP方法能夠有效地提取時序中的弱周期信號，并且能夠減少非均勻采樣產(chǎn)生的虛假信號所帶來的影響.

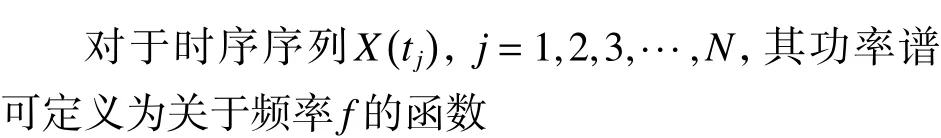
運用LSP方法獲取去除趨勢項后SNR 的頻率后，根據(jù)式(5)反演得出海面高度，如圖3所示.

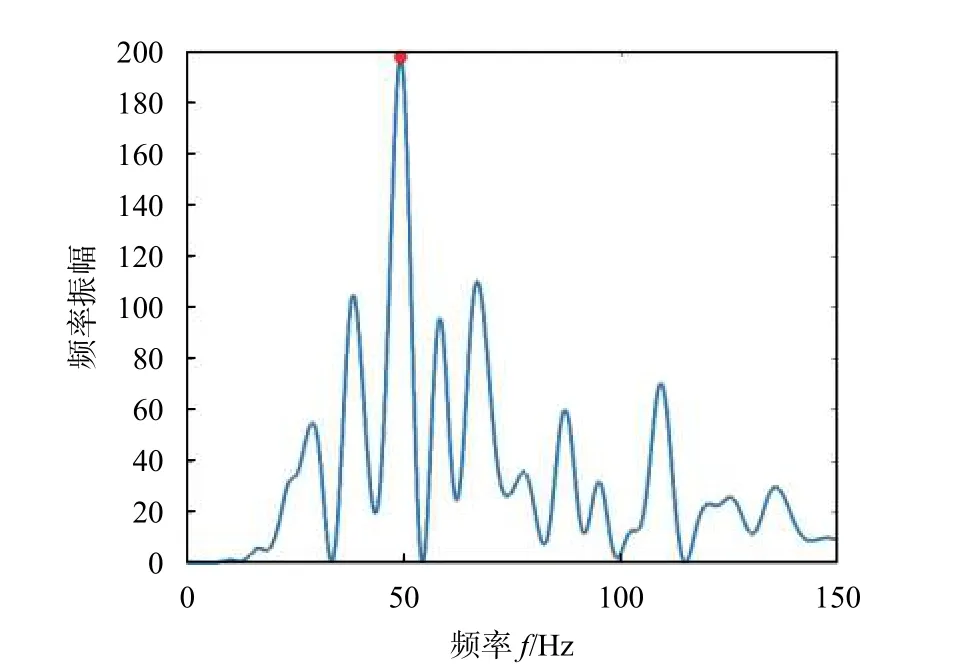
圖3 LSP分析結(jié)果

2.3 小波算法在海面測高中的應(yīng)用

小波分析與傅里葉變換和LSP 相比，傅里葉變換和LSP是全局的變換，得到的是一維的頻域信息，而小波分析是一個時間和頻率的局域變換.因此小波分析能夠有效地從信號中提取信息，解決傅里葉變換所不能解決的諸多問題[33].Wang 等[34]使用小波分析對SNR 信號進行去噪處理，并使用不同長度的SNR信號進行驗證.結(jié)果表明：在較短的SNR 信號中，使用小波分析去噪精度與未使用小波去噪相比提升了20%.Chen 等[35]和蘇曉容等[36]提出了運用小波算法去除噪聲.王杰等[37]提出了運用小波算法提取去除趨勢后的SNR 信號的頻率來反演海面高度的方法.

因為在實際采樣中，SNR 信號是一個離散非連續(xù)的信號，并且使用連續(xù)小波變換計算量太大，所以在處理實際的SNR 信號時使用的是離散小波變換(DWT).將伸縮系數(shù)a和平移因子b進行離散化處理，具體如下：

2.3.1小波去噪原理

1989年，Mallat[38]提出了一種快速DWT 算法，使用小波濾波器分解和重構(gòu)信號，具體如下：

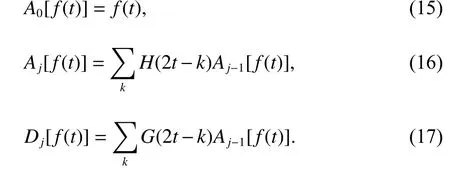
式中：t是離散的時間序列號；f(t)表示原始信號；j是分解信號的層數(shù)；H和G分別是小波的低頻和高頻濾波器.

根據(jù)上述描述，將原始信號通過高通和低通濾波器，將信號分解成低頻部分和高頻部分，然后再將分解的低頻部分再分解成低頻部分和高頻部分，從而實現(xiàn)信號的多層分解.小波分解的原理圖如圖4所示.

將分解出來的高頻系數(shù)進行相應(yīng)小波系數(shù)處理去除噪聲部分，然后再對分解的信號進行重構(gòu)處理，這樣就可以得到去除噪聲后的SNR 信號.

2.3.2小波算法提取頻率

運用小波變換提取去趨勢后SNR 信號頻率，是將趨勢后的SNR 信號與經(jīng)過拉伸或壓縮后的小波進行比較，通過在不同尺度m>0和不同位置n比較原信號與處理后的小波，可以得到一個關(guān)于兩個變量的函數(shù).對于去除趨勢后的SNR 信號，小波變換可以表示為

針對上述方法，王杰使用美國SC02站數(shù)據(jù)進行驗證.運用小波分析反演海面高度，標準差略高于LSP法，但是其可以極大地提高反演海面高度的時間分辨率.具體結(jié)果如表2所示.

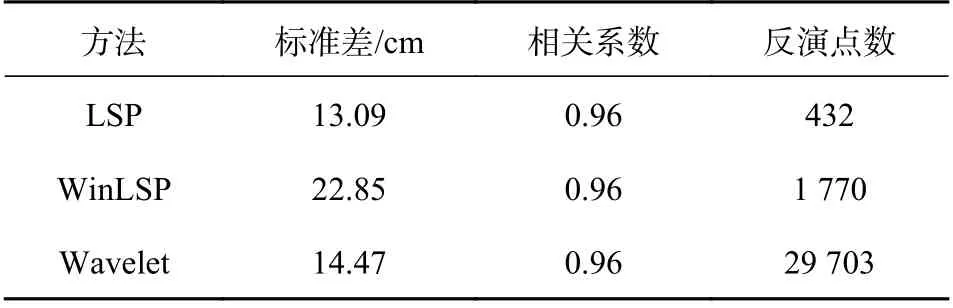
表2 LSP法、加窗LSP法和小波法反演結(jié)果

2.4 B樣條函數(shù)和卡爾曼濾波在海面測高的應(yīng)用

2.4.1 B樣條函數(shù)在海面測高的應(yīng)用

2016年Strandberg[29]提出使用B樣條函數(shù)對海面高度進行建模，該方法考慮到監(jiān)測的海平面是連續(xù)變化的，可以將海面高度變化假設(shè)為一個平滑函數(shù).將海面高度變化作為分段線性模型進行建模可能是最為簡單的方法，但是分段線性模型在計算一階導(dǎo)數(shù)時會導(dǎo)致節(jié)點處的不連續(xù)，不能對海面高度提供足夠的可變性用來考慮次日和長期的海平面變化.B樣條函數(shù)的基本函數(shù)定義為

2.4.2卡爾曼濾波在海面測高的應(yīng)用

之前通過SNR 數(shù)據(jù)反演海面高度的方法是提取接收機接收的一段時間內(nèi)的SNR 信號數(shù)據(jù)，提取出含有高度信息的頻率，然后反演海面高度，該方法只能得出該時間內(nèi)的平均海面高度，并不能提供實時的海面高度數(shù)據(jù).卡爾曼濾波[39]是當前應(yīng)用最廣的一種動態(tài)數(shù)據(jù)處理方法，但原始的卡爾曼濾波是建立在線性系統(tǒng)的基礎(chǔ)上的，對非線性系統(tǒng)效果并不理想[40].在2000年，Merwe等[41]提出無損卡爾曼濾波處理(UKF)更新步驟中的非線性.在2019年，Strandberg等[42]提出了運用無損卡爾曼濾波實現(xiàn)實時監(jiān)測海面高度.該方法采用了一個預(yù)測方程，可以預(yù)測狀態(tài)向量和協(xié)方差矩陣的變換，即：

采用二次B樣條函數(shù)來描述海面高度隨時間的變化，我們需要估計一組縮放系數(shù)αi就可以在任何時間預(yù)測海面高度，即

B樣條函數(shù)定義如式(19)～(20)所示，如式(34)所示，想要知道某個時間點所對應(yīng)的高度，只需要知道該時間點附件的4個節(jié)點.隨著卡爾曼濾波隨著時間的推移，4個節(jié)點B樣條系數(shù)和相應(yīng)的協(xié)方差會不斷的更新，直到引入tj+1處的新節(jié)點.然后將最后一個節(jié)點從狀態(tài)向量中刪除，將前3個節(jié)點往后移，為新的節(jié)點釋放空間.這樣卡爾曼濾波便可以連續(xù)且實時的估計海面的高度.

針對上述方法，Strandberg 使用GTGU 站數(shù)據(jù)進行驗證.卡爾曼濾波法誤差為1.98 cm，并且隨著時間的推移，誤差縮小為1.48 cm.同樣的實驗數(shù)據(jù)，使用LSP方法的誤差為8.84 cm.

3 結(jié)束語

GNSS-R 遙感作為一個新興的領(lǐng)域，在各個領(lǐng)域中有著廣泛的應(yīng)用.本文主要介紹了GNSS-R 在海面測高的研究進展，著重介紹了使用SNR 數(shù)據(jù)反演海面高度的研究進展.主要利用了最小二乘法，LSP法、小波算法、卡爾曼濾波、B樣條函數(shù)等算法在處理SNR 數(shù)據(jù)進行海面測高的應(yīng)用.目前，基于SNR數(shù)據(jù)測量的方法比之前的基于相位差的方法所需要的設(shè)備更為簡單且安裝更加簡便，更具有應(yīng)用潛力.當前，人工神經(jīng)網(wǎng)絡(luò)發(fā)展迅速，在諸多領(lǐng)域得到廣泛的應(yīng)用.神經(jīng)網(wǎng)絡(luò)特別適合變量之間關(guān)系復(fù)雜、耦合度高難以直接數(shù)學(xué)描述的應(yīng)用場景，在GNSS-R 遙感技術(shù)的其他領(lǐng)域，如海冰遙感、土壤濕度檢測、海面溢油、海面風(fēng)場反演等領(lǐng)域都有成功應(yīng)用.但目前為止，神經(jīng)網(wǎng)絡(luò)并未在海面測高方面有所應(yīng)用，對于提取特征頻率的方面還可以利用神經(jīng)網(wǎng)絡(luò)的優(yōu)勢來提高反演海面高度的精度.