角度類儀器校準方法

王亞倩 經亞純 路景飛 高同山 劉蘊 / 河北省計量監督檢測研究院

0 引言

角度類儀器在各個行業中均有所應用，機械工作臺、車床及切削工作臺的水平位置檢測，建筑工程設備的傾斜角檢測及鐵道系統鐵軌水平度的檢測等都離不開角度類儀器。而角度類儀器也由笨重復雜的框式水平儀以及條式水平儀等逐漸向數字化、輕便化、可量化的傾角儀轉化。故本文以常見的數顯傾角儀為例，探討了計量行業中針對角度類儀器的測量方法，以供類似儀器的校準工作參考。

1 校準方法的比較

1.1 正弦規和量塊組合（方法一）

正弦規是應用正弦原理，借助量塊產生角度的一種計量器具[1]。將正弦規放置于平板上，被測數顯傾角儀放置在正弦規上，調整數顯傾角儀示值于零位。根據公式sinθ=d/L（θ為所需角度；d為量塊尺寸；L為正弦規兩側圓柱中心距），計算出需要校準的角度所需量塊尺寸。依次在正弦規的圓柱下放置相應校準點所需尺寸的5等量塊，使正弦規與平板形成相應角度，逐個讀取數顯傾角儀示值，校準示意圖見圖1。數顯傾角儀示值與正弦規產生的相應標準角度值之差為各校準點的示值誤差。此種校準方法優點為所用標準器為一般計量機構均具備的正弦規與5等量塊，便于測量的開展。缺點為使用該方法時，需要計算校準角度所對應尺寸的量塊，但量塊尺寸值有限，當校準某一具體角度值時，可能無法配置組合相應尺寸的量塊，導致無法校準任意角度，具有一定的局限性。

圖1 正弦規和量塊組合校準數顯傾角儀

1.2 光學分度頭（方法二）

光學分度頭是以光學度盤、圓光柵或圓感應同步器等為分度元件的測角儀器，在其圓周或者任意角度內可進行角度測量。校準數顯傾角儀時，將數顯傾角儀吸附在光學分度頭中心軸附件上，置于水平位置。將光學分度頭置于某一個整分度線處，傾角儀示值置于零位，按照校準角度轉動光學分度頭，傾角儀隨之轉動，如圖2所示。傾角儀示值與光學分度頭轉動角度之差即為該點的示值誤差。此種測量方法優點為可校準任意角度，準確度高、直觀性強，無需過多計算，操作簡便易行。不足之處為光學分度頭儀器成本較高，檢測過程中存在兩次對線誤差，人為因素引入的誤差相對較多。

圖2 光學分度頭校準數顯傾角儀

1.3 水平尺測量儀（方法三）

水平尺測量儀依據JJF 1085-2002《水平尺校準規范》[2]附錄B專用檢具技術要求定制而成，包括專用校準臺、專用45°角尺、專用平面平行柱，分別可形成標準的0°、45°（135°）、±90°，如圖3所示。校準時將數顯傾角儀緊貼在水平尺測量儀的工作面上，以此校準相應點，如圖4所示。使用水平尺測量儀校準數顯傾角儀，優點為快捷直觀，針對工作量大、要求不高的角度類器具的校準具有很大優勢。缺點為此檢具為專用設備，需定做，并對其平面度、平行度等有具體要求，且只能測量其固定的幾個角度，無法滿足其他特殊點的校準要求。

圖3 水平尺測量儀

圖4 水平尺測量儀校準數顯傾角儀

2 三種方法校準數顯傾角儀測量不確定度分析與比較

針對三種方法均能校準的45°校準點，以分度值為0.05°的數顯傾角儀為例，分析三種校準方法校準的不確定度。

2.1 測量模型

Δα=αi-α

式中：Δα—— 數顯傾角儀示值誤差，（°）；

αi—— 數顯傾角儀示值，（°）；

α—— 標準器產生的標準值，即45°

2.2 方差和靈敏系數

2.3 不確定度來源

三種校準方法的不確定度來源均為兩大項，即被測數顯傾角儀的重復性和所用標準器引入的不確定度分量。

2.3.1 正弦規和量塊組合校準[3][4]

1）由測量重復性引入的標準不確定度分量u11

此分量可以通過連續測量形成的測量列得到，連續測量10次，得到測量列45.00°、45.05°、45.00°、45.05°、45.00°、45.00°、45.00°、45.05°、45.00°、45.05°。

單次測量的標準差

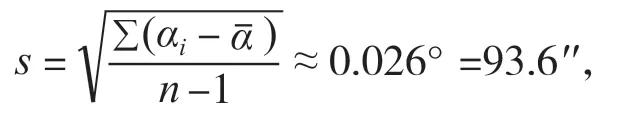
則u11=s= 93.6′′

2）標準器引入的不確定度分量u12

（1）正弦規兩圓柱軸線間距誤差引入的不確定度分量u121

查閱 JJG 37-2005《正弦規》檢定規程可知，兩圓柱中心距的偏差要求 ±1 μm，換算成角度偏差為±1.03′′。

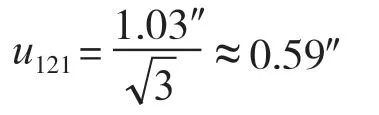
（2）量塊示值誤差引入的不確定度分量u122

量塊與200 mm的正弦規組成45°角，根據公式sinθ=d/L計算所需量塊尺寸d為141.42 mm（選配量塊組合方案：100 mm+40 mm+1.42 mm）。查閱JJG 146-2011《量塊》檢定規程[5]可知，100 mm量塊長度最大極限偏差為±2.5 μm；40 mm 量塊長度最大極限偏差為±1.6 μm；1.42 mm 量塊長度最大極限偏差為±1.0 μm，總最大極限偏差為 ±5.1 μm，換算成角值偏差為±7.28′′。統計分析該分量接近均勻分布，包含因子為則

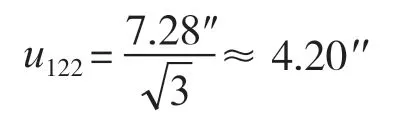
（3）平板平面度誤差引入的不確定度分量u123

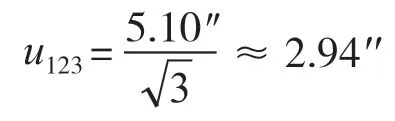
因（1）（2）（3）互不相關，可得標準器引入的不確定度分量測量重復性與標準器引入的不確定度分量彼此獨立，互不相關，則合成標準不確定度為

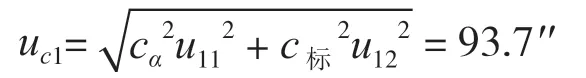
擴展不確定度Uc1由合成標準不確定度uc1與包含因子k= 2得到

Uc1=kuc1= 2×93.7′′= 187.4′′ ≈0.052°

2.3.2 光學分度頭測量

1）由測量重復性引入的標準不確定度分量u21

得到分量的方法如2.3.1中1）所述，u21= 93.6′′

總而言之，雙源CT引導下，相較于普通CT而言，實施經皮穿刺活檢術的安全性、準確性更高，隨著現代醫療設備的不斷完善和更新，雙源CT引導下對胸腹部占位性病變患者實施經皮穿刺活檢術，必然會在臨床中進一步得到廣泛應用。

2）標準器引入的不確定度分量u22

（1）光學分度頭示值誤差引入的不確定度分量u221。校準所用光學分度頭示值誤差為6′′，半寬區間為3′′，按照均勻分布，包含因子為

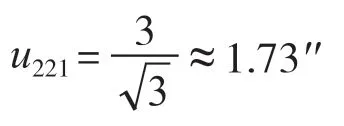
（2）校準過程中對線誤差引入的不確定度分量u222。對線誤差為±1′′，按照均勻分布，包含因子為校準過程中存在兩次對線誤差，故

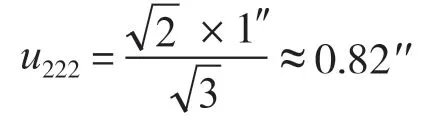
擴展不確定度Uc2由合成標準不確定度uc2與包含因子k= 2得到

Uc2=kuc2= 2×93.6′′= 187.2′′ ≈0.052°

2.3.3 水平尺測量儀測量

1）由測量重復性引入的標準不確定度分量u31

得到分量的方法如2.3.1中1）所述，u31= 93.6′′

2）標準器帶來的不確定度分量u32

45°檢具引入的不確定度分量u32。45°檢具的角度誤差為20′′，均勻分布，故

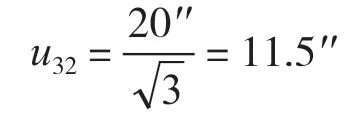
測量重復性與標準器引入的不確定度分量彼此獨立，互不相關，則合成標準不確定度為

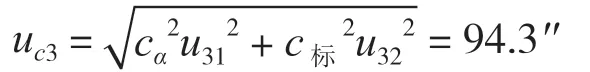
擴展不確定度Uc3由合成標準不確定度uc3與包含因子k= 2得到

Uc3=kuc3= 2×94.3′′= 188.6′′ ≈0.052°

綜上所述，三種測量方法的不確定度分量見表1。

表1 標準不確定度匯總

對于分辨力0.05°數顯傾角儀而言，示值最大允許誤差為±0.2°，以上三種測量方法評定其示值誤差測量結果的擴展不確定度U= 0.052°，k= 2，滿足U≤1/3×MPEV判定準則的要求，因此，可判斷上述三種校準方法均合理可行。同理可得，分辨力為0.01°的數顯傾角儀，示值最大允許誤差為±0.05°，其不確定度用上述三種方法計算可得U= 0.016°，k= 2，均滿足計量要求。且由相關數據可知，不確定度分量主要由測量重復性組成，標準器引入的不確定度分量可控制在一定范圍內，因此，校準更高準確度角度類計量器具時，均可用此三種方法。

3 結語

在計量工作中，經常遇到角度類計量器具的校準檢測，本文通過常見的數顯傾角儀校準，分列了三種常見、可行的方法，結果表明，均可滿足計量要求。計量工作人員可根據實際情況選擇最便捷、適合的校準方法。另外，可參考本文選擇其他標準器進行校準，例如，利用角度塊也可進行數顯傾角儀的校準，也比較方便可行。