基于改進粒子群算法的EV充電站站址與檢測工作規劃*

陳年 李波 韓忠 / 泰州市計量測試院

0 引言

近年來，我國電動汽車（Electric Vehicle，簡稱EV）進入飛速發展新階段，成交量連續5年位居全球第一，累計銷售超過480萬輛，占全球機動車銷售總額的一半以上。而充電站的合理規劃與建設是大規模推廣EV的保障，目前我國已經投入使用的交、直流充電樁共計343 998個，到2020年全國范圍新增集中式充換電站超過12萬座，分散式充電站超過480萬個。

但是，目前充電站卻存在著布局不合理，使用率過低等問題，充電樁淪為“擺設”。同時，對EV充電樁的計量性能提供檢測服務成為與人們生活息息相關而又急需解決的問題。因此，對充電站進行適度超前且合理的規劃布局不僅能提高充電站的使用率，還能降低政府和檢驗檢測機構、充電站設備投資建設者、EV用戶的成本，最終促進整個EV產業鏈的發展。

目前，對于充電站站址規劃國內外學者已展開了大量研究。文獻[1]針對目前EV的使用現狀，提出了充電站規劃的因素和遵循的基本原則。文獻[2]將EV用戶的充電距離及路程用電損耗作為最小函數目標，以提高用戶的使用滿意度及經濟效益，達到推廣EV充電站的目的。文獻[3]考慮了充電站的長期規劃效益，但沒有考慮短期內EV保有量變化的影響，沒有對充電站的規劃方案實現動態更新。文獻[4]分析了充電站、分布式系統接入電網對配電系統穩定性的影響，建立了以總投資成本、檢測服務、維護成本和失負荷成本最小為目標函數的配電系統、EV充電站與分布式儲能復合規劃模型，實現了對配電系統的動態規劃和EV充電設施及分布式儲能系統的選址。合理的充電站站址分布也方便今后檢驗檢測機構開展檢定校準服務工作。

考慮到目前國內EV用戶保有量雖處于高速增長狀態，但總體保有量仍處于較低水平，同時國產電池技術、充電樁基礎設施等軟硬件尚不完善，此時合理規劃充電站的站址就顯得舉足輕重。因此，首先從充電站的點需求和流量需求兩個方面考慮，構建以EV充電站設備建設者、EV用戶和檢驗檢測機構三者綜合成本最小目標函數模型；其次，用Voronoi圖結合粒子群算法的改進算法，實現對目標范圍的自動尋優，獲得了充電站站址的最終位置及檢測服務范圍。

1 點需求

點需求主要從宏觀方面預測EV充電負荷的時空分布特征。首先，預測某規劃地區未來EV的保有量，將該地區分成不同的區域，然后依據不同類型土地使用情況、停車分布特性、停車密度等來計算停車需求模型，得到該地區停車需求的時空分布，最終用來決定充電站及充電樁的數量。上述點需求的預測方法通常使用蒙特卡洛算法，該算法簡單、清晰，易于實現。

2 流量需求

流量需求主要考慮EV車主駕駛習慣、天氣、日期、EV狀態、檢驗檢測機構服務能力等多種因素的影響，結合出行者的出行起點與終點類型、出行線路圖、形成所需電量，模擬出路網中總車流量來推算出充電需求，并以此為依據進行充電站站址的規劃。與點需求相比，流量需求充分考慮了EV用戶的實際需求、檢驗檢測的服務能力及路網的實際運行情況，所以，流量需求分析更加具體、到位，能滿足充電需求的動態變化。但該方法難以獲取準確的概率分布模型。流量需求流程如圖1所示。

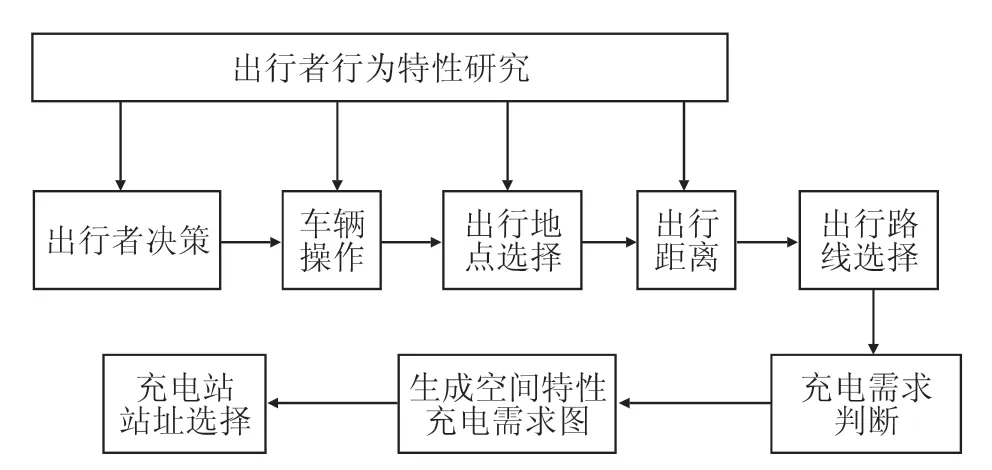
圖1 流量需求

基于流量需求預測充分考慮了出行者的出行特性、公路網的實際情況、檢驗檢測機構服務能力、EV電池特性等，對充電需求時空分布的分析更加細致。采用蒙特卡洛抽樣模擬、博弈論等思想獲取概率分布模型。

3 充電站站址規劃模型

根據流量需求和點需求的充電需求分布情況分析，綜合考慮EV充電站設備建設者、EV用戶和檢驗檢測機構三者綜合成本，建立目標函數：

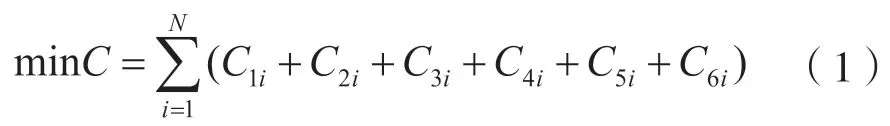
式中：minC—— 充電站折算到每一年的最低費用；

N—— 區域內充電站的數量；

i—— 某個充電站（i= 1，2，3，…，i）；

C1i—— 第i個充電站一次性投資折算到每年的費用；

C2i—— 第i個充電站每年設備維護費用；

C3i—— 第i個充電站電能損耗費用；

C4i—— 第i個充電站基礎設施建設折算到每年的費用；

C5i—— 某個電動汽車用戶成本；

C6i—— 第i個充電站檢驗檢測機構服務成本

1）充電站的一次性投資年費用

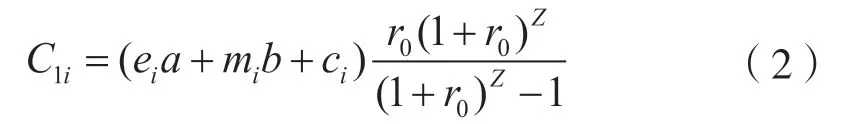
式中：ei—— 充電站變壓器數量；

a—— 變壓器單價；

ci—— 充電站基建成本；

mi—— 充電站的充電機數量；

b—— 充電機價格；

r0—— 充電站的貼現率；

z—— 充電站運行服務年限

2）充電站設備維護成本

充電站的維護成本主要包括設備耗材、設備折舊、工人工資、水電費等。常假設折算系數λ來計算充電站設備維護成本：

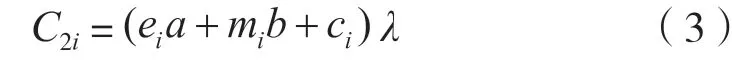
3）充電站電能損耗年費用

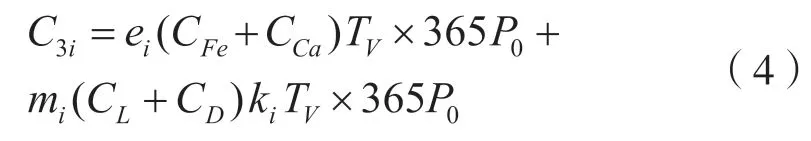
式中：CFe、CCa—— 變壓器鐵耗和銅耗；

Tv—— 充電站充電時長；

P0—— 電網電價（用戶充電電價）；

CL—— 線路損耗；

CD—— 充電機自身損耗；

ki—— 充電機的同時率

4）充電站基礎設施建設年費用

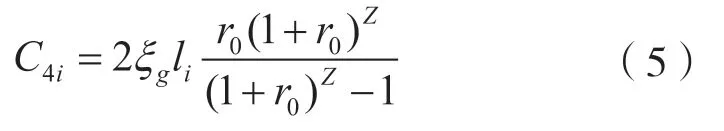
式中：ξg—— 每千米道路投資成本；

li—— 充電站連接到主干道的鋪軌長度

5）EV用戶成本

EV用戶成本由充電往返途中的電量損耗成本和用戶時間成本組成，其數學表達式為[5]

式中：V（j） —— 充電站服務范圍內需求點集合；

j—— 充電服務范圍內某一需求點；

dij—— 需求點j與充電站的距離；

nev,j—— 需求點j的EV數量；

η—— 充電用戶需求比例；

g—— 單位電量可行駛里程

6）檢驗檢測機構服務成本

式中：q—— 檢驗檢測機構時間服務成本；

N—— 需要提供檢驗檢測服務的充電站數量；

t—— 檢測某個充電站所花費的時間；

m—— 檢測儀器折算到單位工作時間的成本

4 模型求解及仿真分析

4.1 模型求解

Voronoi圖是俄國數學家G. Voronoi提出的，并將其擴展至高維空間。目前，Voronoi圖已被廣泛應用在幾何信息相關的許多領域，如空間中求每一個多邊形內的任意一點到本多邊形母點的最短距離，這與充電站的選址思路相近，但Voronoi圖卻削弱全局尋優能力；而粒子群算法源于對鳥群捕食行為的研究，作為一種重要的優化算法已經成功地應用于函數優化、極值尋優、神經網絡訓練等領域。主要通過個體之間信息變化的共享，使整個種群的運動變成一種有序的推進狀態。用xi表示每個粒子的位置，其結果對應一個規劃問題的最優解；即

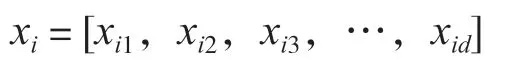
式中：d—— 粒子的維度，即充電站的數量；

xid—— 第i個粒子是否選擇第d個充電站，其值為0或1，表達式為

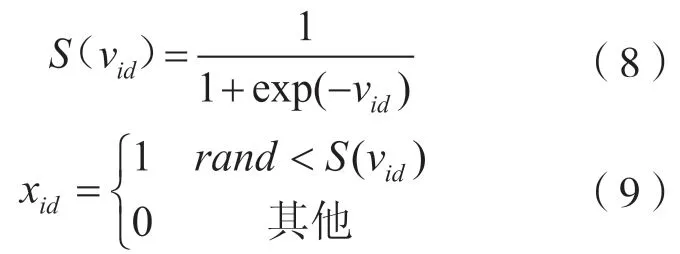
式中：S(vid) —— 位置xid取1的概率；

vid—— 粒子的速度

由式（9）可得，粒子位置為1的概率是S(vid)，為0 的概率是1 -S(vid)。

但上述粒子群算法在實際應用中也存在一些問題，如：全局尋優能力較差、易出現早熟現象、收斂速度慢等。因此，對粒子群算法做如下改進：

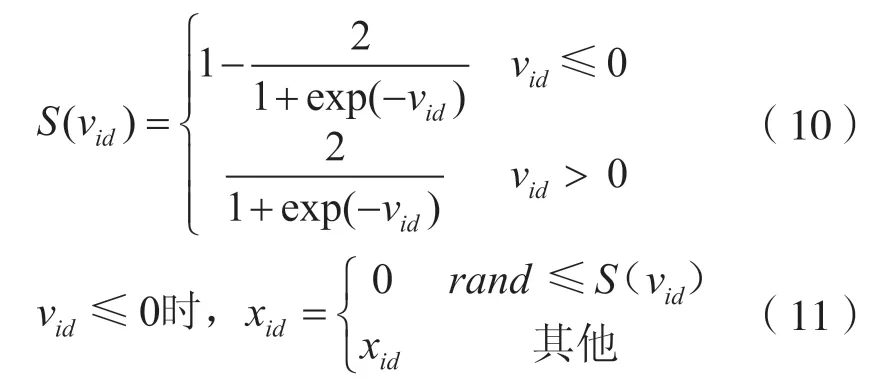
當粒子速度小于或趨于0時，粒子位置發生改變的概率為0；當粒子速度為0 時位置值不變；當粒子速度為正時，粒子位置可能變為1；改進后粒子群算法收斂速度加快，局部搜索能力增強。因此，采用Voronoi圖結合粒子群算法進行模型求解，具體流程如圖2所示。

圖2 算法流程

4.2 仿真分析

本文選定城市中比較有代表性的路段進行合理分析，路網節點36個，并以數字1～36號標注；通過使用MATLAB工具箱對提出的選址模型進行動態仿真，其相關參數參照文獻[6]，同時，預估該區域充電站數量為4～10個。

由圖3可以看出，當該區域修建5個充電站時全社會的成本最小。圖4根據充電站的規劃得到具體的檢測服務劃分范圍，充電站A輻射節點為1、2、10、11、14；充電站B輻射節點為24、25、26、34、35、36；充電站C輻射節點為15、16、17、21、22、23、27、28 ；充電站D輻射節點為3、4、5、6、7、8、9；充電站E輻射節點為18、19、29、30、31、32。圖5為粒子群算法適應度收斂曲線，由于適應度下降速度快，進而更好地達到了收斂的效果。通過圖3～圖5，證明了所提出算法的可靠性，最終得到了合理的規劃選擇。

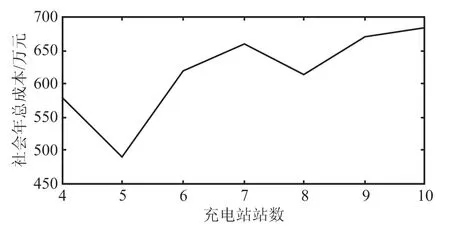
圖3 充電站規劃社會年總成本曲線

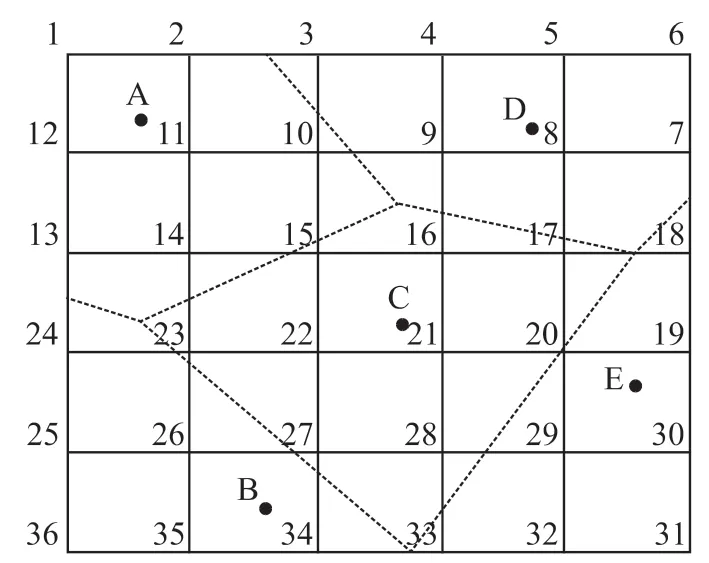
圖4 充電站站址和服務范圍

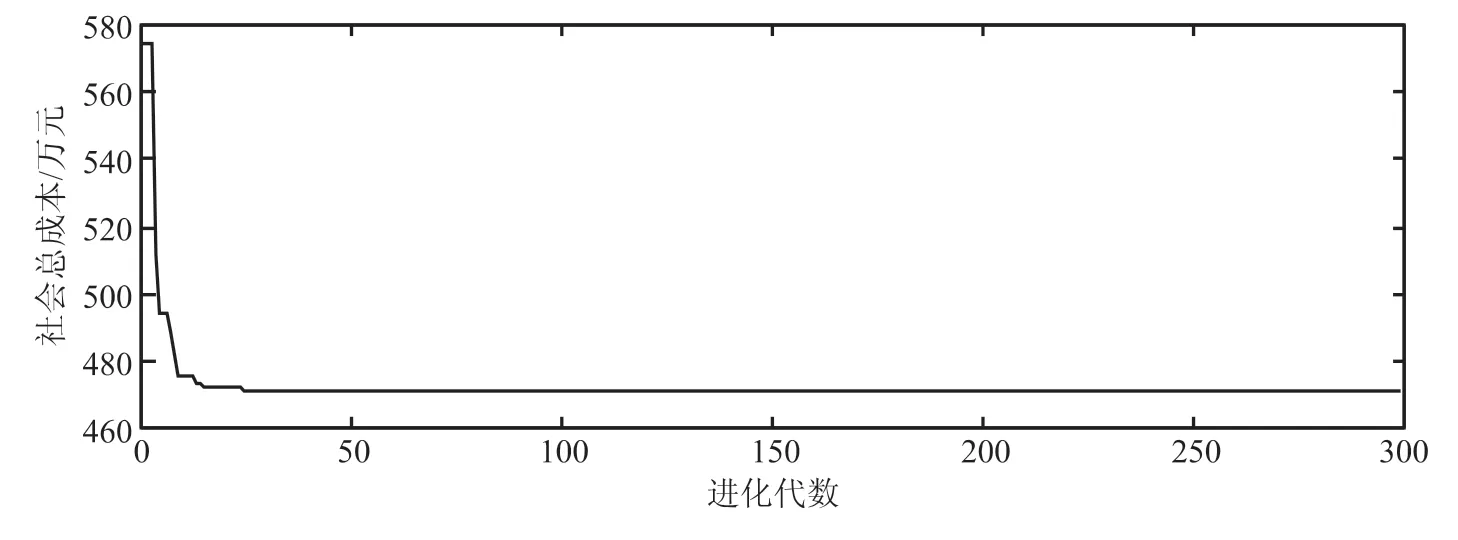
圖5 算法收斂曲線

5 結語

構建EV充電站設備建設者、EV用戶和檢驗檢測機構的綜合成本最小目標函數模型。通過構建改進的粒子群算法，結合Voronoi圖對規劃的路段進行仿真分析。結果表明，規劃的充電站站址分布均勻，服務范圍明確，社會總成本較低，對未來充電站站址的規劃具有參考意義。后續可建立充電站的周期檢定、出廠檢測、安全巡檢為一體的智能化檢驗檢測實驗室，滿足政府監管和市場檢測監測的需求。