基于新維無偏灰色馬爾可夫模型的小麥產(chǎn)量預(yù)測
李曄 白雪

摘要:針對小麥產(chǎn)量具有較大波動(dòng)性的特點(diǎn),結(jié)合灰色預(yù)測模型和馬爾可夫理論,同時(shí)利用新信息優(yōu)先的思想,以河南省2010—2019年小麥產(chǎn)量作為原始數(shù)據(jù)建立無偏灰色GM(1,1)模型、無偏灰色馬爾可夫模型和新維無偏灰色馬爾可夫模型,并對比3種模型的預(yù)測精度。結(jié)果表明,新維無偏灰色馬爾可夫模型能提高預(yù)測精度,適合中長期預(yù)測,并預(yù)測出河南省未來5年的小麥產(chǎn)量數(shù)據(jù)。
關(guān)鍵詞:河南省;小麥;新維無偏灰色馬爾可夫模型;產(chǎn)量預(yù)測
中圖分類號: F326.11? 文獻(xiàn)標(biāo)志碼: A
文章編號:1002-1302(2021)15-0181-05
收稿日期:2020-10-26
基金項(xiàng)目:河南省高等學(xué)校重點(diǎn)科研項(xiàng)目(編號:20A630015);河南省軟科學(xué)研究計(jì)劃(編號:182400410375);河南省高等學(xué)校人文社會(huì)科學(xué)研究一般項(xiàng)目(編號:2020-ZDJH-140)。
作者簡介:李 曄(1972—),女,河南南陽人,碩士,教授,主要從事灰色系統(tǒng)和物流管理研究。E-mail:zzliye@163.com。
糧食問題是關(guān)系國計(jì)民生的重大戰(zhàn)略問題,解決好糧食問題是人類生存和發(fā)展的社會(huì)基礎(chǔ)[1-2]。隨著全球新冠肺炎疫情不斷的發(fā)展蔓延,糧食安全的意義更為突出。2020年5月份的全國兩會(huì)期間,習(xí)近平總書記強(qiáng)調(diào)“農(nóng)業(yè)基礎(chǔ)地位任何時(shí)候都不能忽視和削弱,手中有糧、心中不慌在任何時(shí)候都是真理”。河南省是我國的糧食主產(chǎn)省,小麥生產(chǎn)作為河南省糧食生產(chǎn)的主導(dǎo)產(chǎn)業(yè),其產(chǎn)量高低不僅關(guān)系到河南省的經(jīng)濟(jì)發(fā)展,還關(guān)系到我國糧食供需平衡和生產(chǎn)安全。因此,科學(xué)準(zhǔn)確地預(yù)測河南省的小麥產(chǎn)量,對保障我國糧食安全具有十分重要的價(jià)值和意義。
目前國外預(yù)測糧食產(chǎn)量的方法主要有氣象產(chǎn)量預(yù)測法[3]、遙感技術(shù)[4]和統(tǒng)計(jì)動(dòng)力學(xué)模擬法[5]這3種。它們的預(yù)測提前期一般為2個(gè)月左右,預(yù)測誤差為產(chǎn)量的5%~10%,精度較低。國內(nèi)預(yù)測糧食產(chǎn)量的方法主要分為2類。一類是傳統(tǒng)的線性建模預(yù)測法,主要包括投入產(chǎn)出模型預(yù)測法,線性回歸預(yù)測法和指數(shù)平滑法等。陳錫康等利用投入占用產(chǎn)出技術(shù)預(yù)測了我國未來幾年的糧食產(chǎn)量[6];劉東等基于向前選擇法的多元線性回歸模型來預(yù)測糧食產(chǎn)量的發(fā)展趨勢[7];何延治等利用時(shí)間序列分析中的 ARIMA(p,d,q)模型預(yù)測了吉林省糧食產(chǎn)量[8];吳越等分別使用Holt兩參數(shù)指數(shù)平滑法和ARIMA模型預(yù)測2019—2023年長三角地區(qū)的糧食產(chǎn)量,預(yù)測效果理想[9]。另一類是非線性模型預(yù)測法,主要包含灰色預(yù)測、BP神經(jīng)網(wǎng)絡(luò)、馬爾可夫模型和粗糙集理論等。樊超等利用灰度極限學(xué)習(xí)機(jī)模型預(yù)測我國糧食產(chǎn)量,為準(zhǔn)確預(yù)測短期糧食產(chǎn)量提供了一種新的技術(shù)手段[10];李炳軍等利用灰色區(qū)間預(yù)測和 GM(1,N) 模型分別預(yù)測了我國主要糧食的需求量和產(chǎn)量[11];楊陽利用尾端殘差修正的 GM(1,1) 模型預(yù)測了我國人均糧食產(chǎn)量,預(yù)測精度提高[12];郭亞菲等利用粒子群優(yōu)化神經(jīng)網(wǎng)絡(luò)的模型預(yù)測糧食產(chǎn)量,為糧食產(chǎn)量預(yù)測提供了新的途徑[13];尹宗成基于粗糙集理論預(yù)測了我國的糧食產(chǎn)量[14];張文政等通過比較線性回歸、支持向量機(jī)和隨機(jī)森林這3種方法的預(yù)測精度[15],最后選用精度較高的支持向量機(jī)預(yù)測了遼寧省的糧食產(chǎn)量。
線性建模預(yù)測法雖然建模簡單,容易實(shí)現(xiàn),可以清楚地了解各個(gè)變量之間的關(guān)系,但是需要收集大量數(shù)據(jù)才能提高預(yù)測的精度,而且僅適用于短期糧食產(chǎn)量預(yù)測。非線性模型預(yù)測法彌補(bǔ)了傳統(tǒng)預(yù)測方法的許多缺陷,然而由于小麥生產(chǎn)受氣候、環(huán)境和政策等多種因素影響,導(dǎo)致其產(chǎn)量數(shù)據(jù)具有較大的波動(dòng)性。以上預(yù)測方法均不適合對隨機(jī)波動(dòng)性較大的小麥產(chǎn)量進(jìn)行中長期預(yù)測。
為了彌補(bǔ)這一缺陷,提高河南省小麥產(chǎn)量的預(yù)測精度,解決中長期預(yù)測的波動(dòng)問題,本研究采用新維無偏灰色馬爾可夫模型[16-17]進(jìn)行分析預(yù)測。在無偏GM(1,1)模型的基礎(chǔ)上利用馬爾可夫鏈修正預(yù)測值殘差,同時(shí)引入新信息優(yōu)先的思想,不斷更新原始數(shù)據(jù),應(yīng)用于河南省小麥產(chǎn)量預(yù)測,不僅保留了短期預(yù)測的高精度,而且提高了中長期的預(yù)測精確度。
1 模型構(gòu)建
1.1 無偏GM(1,1)模型的構(gòu)建
吉培榮等對傳統(tǒng)GM(1,1)模型的性質(zhì)做了相關(guān)研究,證明傳統(tǒng)GM(1,1)模型是有偏差的指數(shù)模型,基于此提出無偏GM(1,1)模型[18]。具體建模過程如下:
設(shè)原始序列為
X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]。(1)
其中,x(0)(k)≥0,k=1,2,…,n。
(1)對X(0)做一次累加生成得
X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]。(2)
其中,
x(1)(k)=∑ki=1x(0)(i),k=1,2,…,n。(3)
(2)確定數(shù)據(jù)矩陣B,Y。
B=-12[x(0)(1)+x(1)(2)]1
-12[x(1)(2)+x(1)(3)]1
-12[x(1)(n-1)+x(1)(n)]1,
Y=x(0)(2)x(0)(3) x(0)(n)。(4)
(3)使用最小二乘法,計(jì)算參數(shù)估計(jì)量a,u。
a^=[a,u]T=(BTB)-1BTY。(5)
(4)計(jì)算無偏灰色GM(1,1)模型的參數(shù)b,A。
b^=ln2-a2+a A^=2u2+a。(6)
(5)建立原始數(shù)據(jù)序列模型。
x^(0)(1)=x(0)(1),x^(0)(k+1)=Aebk,k=1,2,…,n。(7)
其中,x^(0)(k+1)在k=1,2,…,n-1時(shí)為原始序列的擬合值,在k≥n時(shí)為原始序列的預(yù)測值。
1.2 無偏灰色馬爾可夫模型的構(gòu)建
馬爾可夫模型通過狀態(tài)間的轉(zhuǎn)移概率對系統(tǒng)將來的發(fā)展趨勢做出預(yù)測,可對隨機(jī)波動(dòng)序列進(jìn)行長期預(yù)測[19]。無偏灰色馬爾可夫模型是將無偏 GM(1,1) 模型和馬爾可夫模型相結(jié)合建立的[20]。具體步驟如下:
(1)建立無偏GM(1,1)模型,
得到無偏灰色預(yù)測值:X^(0)(1)=X(0)(1),X^(0)(k+1)=Aebk,k=1,2,…,n。
(2)計(jì)算預(yù)測值與實(shí)際值之間的相對誤差。
Q=x(0)(it)-x^(0)(it)x(0)(it)×100%。(8)
(3)狀態(tài)劃分。
根據(jù)預(yù)測值與實(shí)際值之間相對誤差的大小將樣本數(shù)據(jù)劃分為若干狀態(tài),任一狀態(tài)可記為 Ei∈[1i,2i],i=1,2,…,s,其中s為劃分的狀態(tài)數(shù)目,灰元1i和2i分別表示第i種狀態(tài)的上下界。s和1i、2i視具體情況而定。
(4)構(gòu)造狀態(tài)轉(zhuǎn)移概率矩陣。
設(shè)N(n)ij為由狀態(tài)Ei經(jīng)過n步轉(zhuǎn)移到Ej的頻數(shù),Ni為狀態(tài)Ei出現(xiàn)的頻數(shù),則由狀態(tài)Ei經(jīng)過n步轉(zhuǎn)移到Ej的概率為
p(n)ij=N(n)ijNi,i,j=1,2,…s。(9)
從而得到狀態(tài)轉(zhuǎn)移概率矩陣為
p(n)=p(n)11p(n)12…p(n)1s
p(n)21p(n)22…p(n)2s
p(n)s1p(n)s2…p(n)ss。(10)
(5)計(jì)算預(yù)測值。
結(jié)合狀態(tài)轉(zhuǎn)移概率矩陣,確定系統(tǒng)將來最可能所處的狀態(tài),進(jìn)一步得出預(yù)測值的變動(dòng)區(qū)間[1i,2i],取此區(qū)間的中值作為修正值y,具體公式為
y=x^(0)(k)×1±12(1i+2i)。(11)
1.3 新維無偏灰色馬爾可夫模型的構(gòu)建
隨著時(shí)間的不斷推移,灰色系統(tǒng)中會(huì)有一些隨機(jī)擾動(dòng)因素不斷加入,從而影響系統(tǒng)發(fā)展;預(yù)測的時(shí)間越遠(yuǎn),模型的精度越低。為了提高模型的預(yù)測精度,引入新維無偏灰色馬爾可夫模型[21],對原始數(shù)據(jù)序列做等維信息處理,即將最新得到的預(yù)測值加入到已知序列,同時(shí)刪去序列中的第1個(gè)數(shù)據(jù),然后對新得到的數(shù)據(jù)序列再次進(jìn)行無偏灰色馬爾可夫預(yù)測,這樣反復(fù)對原始數(shù)據(jù)進(jìn)行實(shí)時(shí)修正,直到完成預(yù)測目標(biāo)。由于新維無偏灰色馬爾可夫模型不斷增加新信息并同時(shí)刪除舊信息,得到的新序列可以更好地反映系統(tǒng)的當(dāng)前特征,進(jìn)而提高中長期的預(yù)測精度[22-23]。
2 基于新維無偏灰色馬爾可夫模型的河南省小麥產(chǎn)量預(yù)測
河南省小麥產(chǎn)量受環(huán)境、天氣和政策等多方面因素的影響,具有較大的波動(dòng)性,有效預(yù)測河南省小麥產(chǎn)量的變化趨勢,提升預(yù)測精度,是增加其產(chǎn)量的關(guān)鍵。無偏GM(1,1)模型適用于預(yù)測隨機(jī)波動(dòng)性不大的時(shí)間序列變化趨勢,如果用來預(yù)測波動(dòng)性較大的小麥產(chǎn)量數(shù)據(jù)會(huì)使其預(yù)測精度變差[24]。馬爾可夫模型適用于具有非平穩(wěn)隨機(jī)特點(diǎn)的序列預(yù)測,因此,結(jié)合無偏GM(1,1)模型與馬爾可夫模型,使2個(gè)模型優(yōu)勢互補(bǔ),能夠預(yù)測序列的發(fā)展趨勢且提高預(yù)測精度,在小麥產(chǎn)量預(yù)測方面有較強(qiáng)的理論意義和實(shí)用價(jià)值。
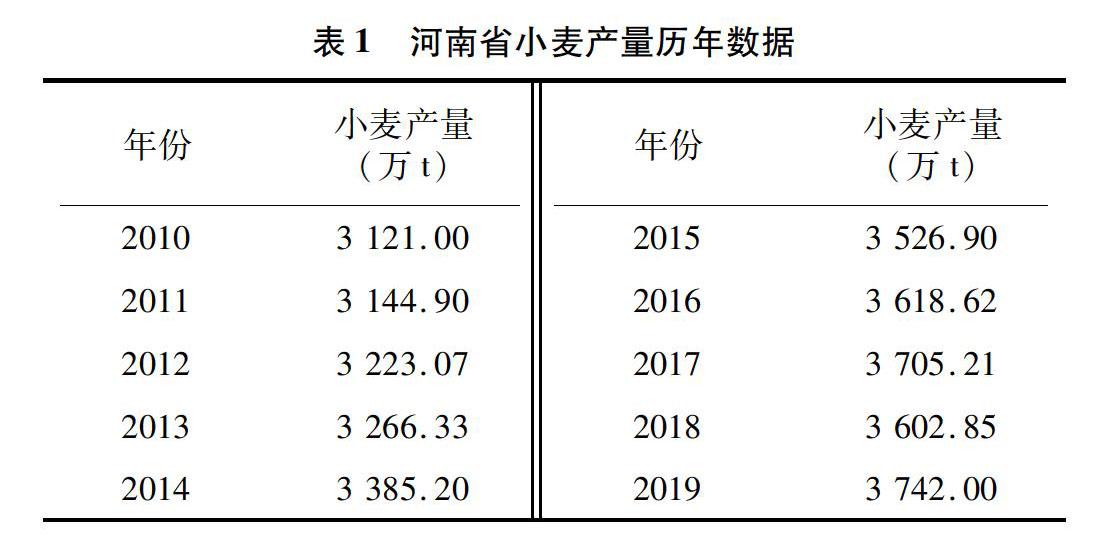
選取2010—2019年的河南省小麥產(chǎn)量數(shù)據(jù)作為原始數(shù)據(jù)(表1),數(shù)據(jù)源于《河南省統(tǒng)計(jì)年鑒》。
2.1 無偏GM(1,1)模型預(yù)測
根據(jù)無偏GM(1,1)模型的建模原理,結(jié)合表1中2010—2019年河南省小麥產(chǎn)量數(shù)據(jù),使用灰色建模軟件第7版和Matlab 2016b可以得到相應(yīng)的時(shí)間響應(yīng)函數(shù):
X^(0)(1)=X(0)(1)=3 131.00,X^(0)(k+1)=Aebk=3 096.69e0.02k,k=1,2,…,n。(12)
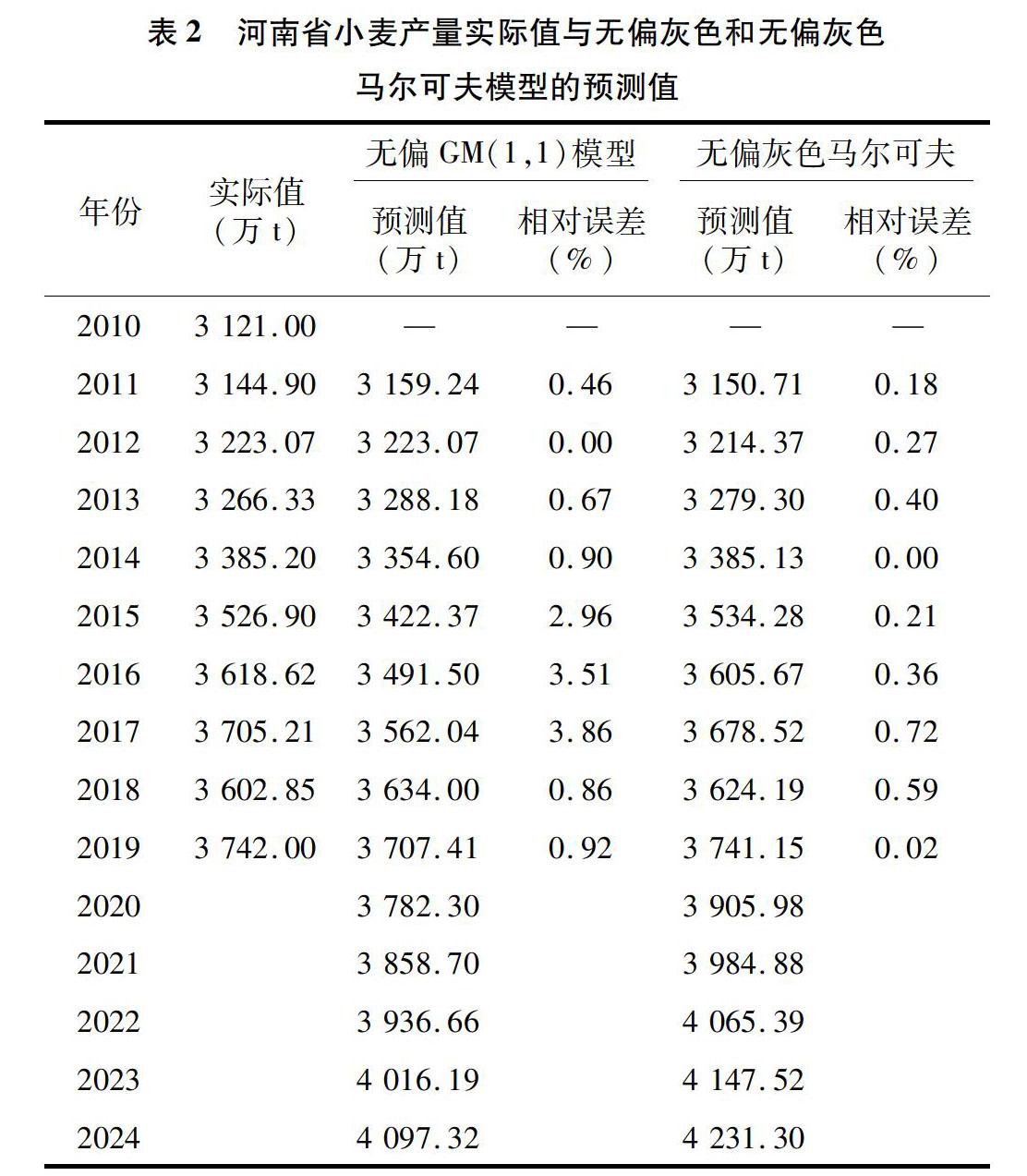
預(yù)測結(jié)果見表2,該模型的平均相對誤差為1.57%。
2.2 馬爾可夫鏈修正灰色預(yù)測值
無偏灰色GM(1,1)預(yù)測模型反映出小麥產(chǎn)量數(shù)據(jù)的指數(shù)變化規(guī)律,并根據(jù)該規(guī)律外推可得出預(yù)測值。受氣候、環(huán)境、政策等多方面因素影響,單一模型不能刻畫小麥產(chǎn)量的變化趨勢,因此,引入馬爾可夫模型修正殘差,充分發(fā)揮其在預(yù)測離散隨機(jī)波動(dòng)大的事件上的優(yōu)勢,彌補(bǔ)灰色預(yù)測模型的不足。
2.2.1 狀態(tài)劃分
根據(jù)河南省小麥產(chǎn)量的實(shí)際值和無偏GM(1,1)模型得出預(yù)測值之間的相對誤差,
將小麥產(chǎn)量的數(shù)據(jù)序列劃分為4個(gè)區(qū)間:E1(-0.86,0.32)、E2(0.32,1.50)、E3(1.50,2.68)、E4(2.68,3.86)。河南省小麥產(chǎn)量預(yù)測年份的所處狀態(tài)見表3。
由于河南省小麥產(chǎn)量2011—2019年的所處狀態(tài)已知,令對應(yīng)區(qū)間的中點(diǎn)作為擬合值。如2011年小麥產(chǎn)量處于狀態(tài)1,則2011年小麥產(chǎn)量的擬合值為:
X2011=3 159.24-3 159.24×0.5×(-0.86%+0.32%)=3 150.71。(13)
同理,可以擬合2012—2019年河南省小麥產(chǎn)量,擬合值見表2。
2.2.2 構(gòu)造狀態(tài)轉(zhuǎn)移概率矩陣
由狀態(tài)劃分表及各年對應(yīng)的狀態(tài),可得1步和2步轉(zhuǎn)移概率矩陣:
p1=121200
0001
0000
130023
p2=1414012
130023
0000
71816049。(14)
2.2.3 確定預(yù)測值
因?yàn)?019年小麥產(chǎn)量處于狀態(tài)4,根據(jù)1步轉(zhuǎn)移概率矩陣計(jì)算2020年小麥產(chǎn)量數(shù)據(jù):
X2020=3 782.30-3 782.30×0.5×(2.68%+3.82%)=3 905.98。(15)
同理可根據(jù)2步、3步、4步、5步轉(zhuǎn)移概率矩陣計(jì)算2021—2024年小麥產(chǎn)量數(shù)據(jù),分別為3 984.88 萬、4 065.39萬、4 147.52萬、4 231.32萬t。
擬合和預(yù)測結(jié)果見表2,該模型的平均相對誤差為0.31%。
由于傳統(tǒng)無偏灰色GM(1,1)模型沒有考慮河南省歷年小麥產(chǎn)量對未來預(yù)測年份小麥產(chǎn)量的影響,初始預(yù)測值較為準(zhǔn)確,2011—2014年的預(yù)測誤差均小于1%。但隨著年份的不斷增加,小麥年產(chǎn)量之間的相互影響作用以及歷年小麥產(chǎn)量數(shù)據(jù)對未來小麥產(chǎn)量影響逐步降低,導(dǎo)致模型的預(yù)測精度變差。從圖1可以明顯看出,2015—2017年的小麥產(chǎn)量的預(yù)測誤差明顯增加;無偏灰色馬爾可夫模型綜合考慮了序列的波動(dòng)性以及歷年產(chǎn)量對未來年份小麥產(chǎn)量的影響,結(jié)合這2種模型的優(yōu)勢,提高了河南省小麥產(chǎn)量的預(yù)測精度。2011—2019年的預(yù)測誤差均降低到小于0.8%,但仍有個(gè)別年份預(yù)測誤差偏大,如2017年模型的預(yù)測誤差達(dá)到0.72%,模型仍需要進(jìn)一步改進(jìn)。
2.3 新維灰色馬爾科夫模型預(yù)測
影響河南省小麥產(chǎn)量的各方面因素在不停地變化,不斷有新的隨機(jī)擾動(dòng)因素加入系統(tǒng),而且舊數(shù)據(jù)在預(yù)測序列中的有效作用逐步降低,對小麥產(chǎn)量產(chǎn)生重要影響。因此,需對建模原始數(shù)據(jù)序列進(jìn)行實(shí)時(shí)修正。
利用無偏灰色馬爾可夫模型得到的2020年小麥產(chǎn)量預(yù)測值添加到原數(shù)據(jù)序列,同時(shí)剔除第1個(gè)數(shù)據(jù),即2010年小麥產(chǎn)量數(shù)據(jù),以2011—2020年小麥產(chǎn)量數(shù)據(jù)作為新的數(shù)據(jù)序列,然后構(gòu)建無偏灰色GM(1,1)模型
X^(0)(1)=X(0)(1)=3 144.90,X^(0)(k+1)=Aebk=3 179.05e0.02k,k=1,2,…,n
最后通過馬爾可夫模型修正,得到2021年河南省小麥產(chǎn)量預(yù)測值。
由于進(jìn)行1次等維新息處理后,平均相對誤差為0.29%,仍比較大,所以繼續(xù)對建模序列做等維處理。將該值作為2021年小麥產(chǎn)量數(shù)據(jù)重復(fù)使用上述的步驟,得到2022年小麥產(chǎn)量數(shù)據(jù),同理可得2023、2024年小麥產(chǎn)量數(shù)據(jù),其平均相對誤差分別為0.25%、0.22%、0.22%,預(yù)測結(jié)果見表4。
2.4 模型比較
河南省小麥產(chǎn)量是非平穩(wěn)的時(shí)間序列,通過結(jié)合無偏GM(1,1)模型和馬爾可夫模型,并等維處理建模原始數(shù)據(jù)序列,得到新維無偏灰色馬爾可夫模型,該模型充分發(fā)揮了2個(gè)模型的優(yōu)勢,能較好地預(yù)測非平穩(wěn)時(shí)間序列。
通過表5預(yù)測模型的精度對比可以看出,通過馬爾可夫修正對河南省小麥產(chǎn)量預(yù)測的平均相對誤差減小,新維無偏灰色馬爾可夫模型的平均相對誤差低至0.22%,相對最小,精度最高,可以很好地反映河南省小麥產(chǎn)量變化趨勢,在中長期的預(yù)測中更具有優(yōu)勢。
結(jié)合最終預(yù)測結(jié)果和預(yù)測精度檢驗(yàn)可以得出,采用新維無偏灰色馬爾可夫模型預(yù)測出2020—2024年河南省小麥產(chǎn)量分別為3 905.98萬、3 985.99萬、4 067.29萬、4 151.19萬、4 235.40萬t。結(jié)果顯示河南省小麥產(chǎn)量在未來5年都會(huì)呈上升趨勢,但增長速度呈緩慢趨勢。
3 結(jié)論
本研究以河南省小麥產(chǎn)量預(yù)測為例,采用新維無偏灰色馬爾可夫模型,充分利用了灰色預(yù)測建模所需信息量少的特點(diǎn)以及馬爾可夫模型能夠處理隨機(jī)波動(dòng)性數(shù)據(jù)的特性,并利用實(shí)時(shí)修正對模型進(jìn)行優(yōu)化。對河南省2010—2019年小麥產(chǎn)量預(yù)測結(jié)果表明,該模型的預(yù)測精度較高,預(yù)測結(jié)果更精確,可以很好地反映河南省小麥產(chǎn)量變化趨勢,對河南省制定小麥生產(chǎn)規(guī)劃、調(diào)整和優(yōu)化小麥種植結(jié)構(gòu)以及促進(jìn)河南省小麥生產(chǎn)的可持續(xù)發(fā)展具有重要意義。同時(shí),本研究結(jié)果可以為政府相關(guān)決策部門擬定糧食配置和宏觀經(jīng)濟(jì)計(jì)劃提供依據(jù),從而保障我國糧食安全,維護(hù)國民經(jīng)濟(jì)發(fā)展和社會(huì)穩(wěn)定。
參考文獻(xiàn):
[1]楊宗輝,蔡鴻毅,覃 誠,等. 我國糧食生產(chǎn)的時(shí)空格局及其影響因素分析[J]. 中國農(nóng)業(yè)科技導(dǎo)報(bào),2018,20(9):1-11.
[2]陳光軍. 鄉(xiāng)村振興背景下中國改革40年來糧食安全的回顧與思考[J]. 農(nóng)業(yè)經(jīng)濟(jì),2020(3):3-5.
[3]Ajwde W,Cavan D. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts[J]. Agricultural and Forest Meteorology,2007,146(1):38-56.
[4]Rosegrantm W,Ringler C,Roe T L. Asian economic crisis and the long-term global food situation[J]. Food Policy,2000,25(3):243-254.
[5]Jin Z Q,Zhu D W. Impacts of changes in climate and its variability on food production in Northeast China[J]. Acta Agronomica Sinica,2008,34(9):1588-1597.
[6]陳錫康,楊翠紅. 投入占用產(chǎn)出技術(shù)在全國糧食產(chǎn)量預(yù)測及鄉(xiāng)鎮(zhèn)企業(yè)中的應(yīng)用[J]. 中國科學(xué)基金,2003,17(3):149-152.
[7]劉 東,白雪峰,孟 軍. 基于向前選擇變量法的我國糧食總產(chǎn)量多元線性回歸預(yù)測模型[J]. 東北農(nóng)業(yè)大學(xué)學(xué)報(bào),2010,41(10):124-128.
[8]何延治. 基于時(shí)間序列分析的吉林省糧食產(chǎn)量預(yù)測模型[J]. 江蘇農(nóng)業(yè)科學(xué),2014(10):478-479.
[9]吳 越,張煥明. 基于Holt兩參數(shù)指數(shù)平滑法和ARIMA模型的長三角糧食產(chǎn)量的預(yù)測[J]. 武漢輕工大學(xué)學(xué)報(bào),2020,39(1):30-36.
[10]樊 超,曹培格,郭亞菲,等. 基于灰度極限學(xué)習(xí)機(jī)的糧食產(chǎn)量預(yù)測[J]. 江蘇農(nóng)業(yè)科學(xué),2018,46(5):212-214.
[11]李炳軍,楊衛(wèi)明. 基于灰色區(qū)間預(yù)測和GM(1,N)模型的我國糧食供需結(jié)構(gòu)平衡分析[J]. 江蘇農(nóng)業(yè)科學(xué),2019,47(18):325-329.
[12]楊 陽. 基于殘差修正的GM(1,1)模型的我國人均糧食產(chǎn)量預(yù)測[J]. 統(tǒng)計(jì)與決策,2011(17):53-55.
[13]郭亞菲,樊 超,閆洪濤. 基于主成分分析和粒子群優(yōu)化神經(jīng)網(wǎng)絡(luò)的糧食產(chǎn)量預(yù)測[J]. 江蘇農(nóng)業(yè)科學(xué),2019,47(19):241-245.
[14]尹宗成. 運(yùn)用粗糙集理論對我國糧食產(chǎn)量的預(yù)測[J]. 統(tǒng)計(jì)與決策,2008(6):46-48.
[15]張文政,孫德山,王 玥,等. 基于支持向量機(jī)的遼寧省糧食產(chǎn)量預(yù)測[J]. 經(jīng)濟(jì)數(shù)學(xué),2019,36(1):96-99.
[16]李 東,蘇小紅,馬雙全. 基于新維灰色馬爾科夫預(yù)測模型的股價(jià)預(yù)測算法[J]. 哈爾濱工業(yè)大學(xué)學(xué)報(bào),2003,35(2):244-248.
[17]高 陽,譚陽波. 基于新維無偏灰色馬爾科夫預(yù)測模型的中長期能源消費(fèi)預(yù)測[J]. 統(tǒng)計(jì)與決策,2007(22):55-57.
[18]吉培榮,黃巍松,胡翔勇.無偏灰色預(yù)測模型[J]. 系統(tǒng)工程與電子技術(shù),2000,22(6):6-7,80.
[19]張冬詠,陳泗達(dá). 基于灰色-馬爾可夫模型的國內(nèi)游客總數(shù)預(yù)測[J]. 河南科學(xué),2020,38(1):96-101.
[20]王 姍,翟 瓊,許麗娜. 基于灰色馬爾科夫模型的中國女子中長跑成績的預(yù)測[J]. 數(shù)學(xué)的實(shí)踐與認(rèn)識,2016,46(24):161-170.
[21]Li L,Sun L,Ning G. Deterioration of urban bridges on network level using Markov-chain model[J]. Mathematical Problems in Engineering,2014(7):1-10.
[22]陳寶平 .基于新維無偏灰色馬爾科夫模型的圍欄草場面積的預(yù)測[J]. 數(shù)學(xué)的實(shí)踐與認(rèn)識,2013,43(24):58-63.
[23]趙 玲,許宏科. 基于新維無偏灰色馬爾可夫的交通事故預(yù)測[J]. 計(jì)算機(jī)工程與應(yīng)用,2013,49(7):35-38.
[24]向 宇,吳 琴. 改進(jìn)的灰色預(yù)測模型在全國用水量預(yù)測中的應(yīng)用[J]. 湖北民族學(xué)院學(xué)報(bào)(自然科學(xué)版),2015,33(1):25-30.

