PC連續(xù)梁應力水平與長期變形特性

魏漢鋒，黃 勁

(1.廣東省高速公路發(fā)展股份有限公司佛開分公司，廣東 佛山 528051；2.廣東華路交通科技有限公司，廣州 510420)

0 引言

大跨度PC連續(xù)梁以其施工簡便、造價經(jīng)濟、行車舒適等特點，在公路建設中得到了廣泛應用。然而，近年來，PC連續(xù)梁主跨的持續(xù)下?lián)稀⒏拱逍绷芽p、底板開裂等現(xiàn)象頻繁出現(xiàn)，已成為困擾國內(nèi)外同類橋型設計、施工及養(yǎng)護的主要問題[1-3]。

大跨徑預應力混凝土梁橋長期過量下?lián)系膯栴}，究其原因主要是對混凝土材料的徐變收縮預測不足，以及長期預應力損失估計偏低等原因[4]。為分析這一問題，國內(nèi)外進行了相關(guān)預應力混凝土梁長期性能的試驗研究[5-7]，但試驗所采用的預應力混凝土梁模型尺寸小且設計應力水平較低，與目前運營的大跨徑預應力混凝土梁橋?qū)嶋H的高應力狀態(tài)不相符。

基于此，在已有研究成果的基礎(chǔ)上[8-9]，本文通過建立高應力狀態(tài)下的梁體試驗模型，對梁體長期變形與應力狀態(tài)的關(guān)系以及不同應力狀態(tài)下的梁體徐變變形進行試驗研究。設計了高“應力/強度”比值下的PC連續(xù)試驗梁，根據(jù)連續(xù)梁受力狀態(tài)選取跨中截面和中支點截面為試驗的關(guān)鍵截面，分析了試驗梁的預應力損失、跨中截面上緣總應變及徐變應變、中支點截面下緣總應變及徐變應變隨時間的發(fā)展規(guī)律，并與現(xiàn)行規(guī)范的理論計算值進行了比較。同時分析關(guān)鍵截面應力水平，上、下緣應力差對試驗梁長期性能參數(shù)的影響規(guī)律，有利于進一步深入了解梁體徐變對大跨徑橋梁長期變形的影響，為準確預測大跨度預應力混凝土梁橋的長期變形提供理論基礎(chǔ)。

1 試驗方案

1.1 試驗梁

試驗共設計了4片連續(xù)試驗梁，采用矩形截面，其截面幾何尺寸為18cm×22cm，長度為3.8m，計算跨徑為1.8m。梁體中配置φs15.2低松弛預應力鋼絞線，試驗中通過調(diào)整鋼絞線的錨下張拉力來控制混凝土梁截面的應力狀態(tài)。

由于梁體的應力水平越高，上、下緣應力差越大，則梁體徐變及長期變形越大[10]。試驗中，4片連續(xù)試驗梁的應力水平各不相同，當分析梁體上緣應力水平對跨中長期變形的影響時，需保持梁體上、下緣應力差基本相同，分為2組：AA組(PCC1、PCC3)、BB組(PCC2、PCC4)。當分析梁體上、下緣應力差對跨中長期變形的影響時，需保持梁體上緣應力水平基本相同，分為2組：CC組(PCC1、PCC2)、DD組(PCC3、PCC4)。

表1為各試驗梁的關(guān)鍵截面初始應力狀態(tài)、單股預應力鋼束張拉力及跨中的集中荷載布置。

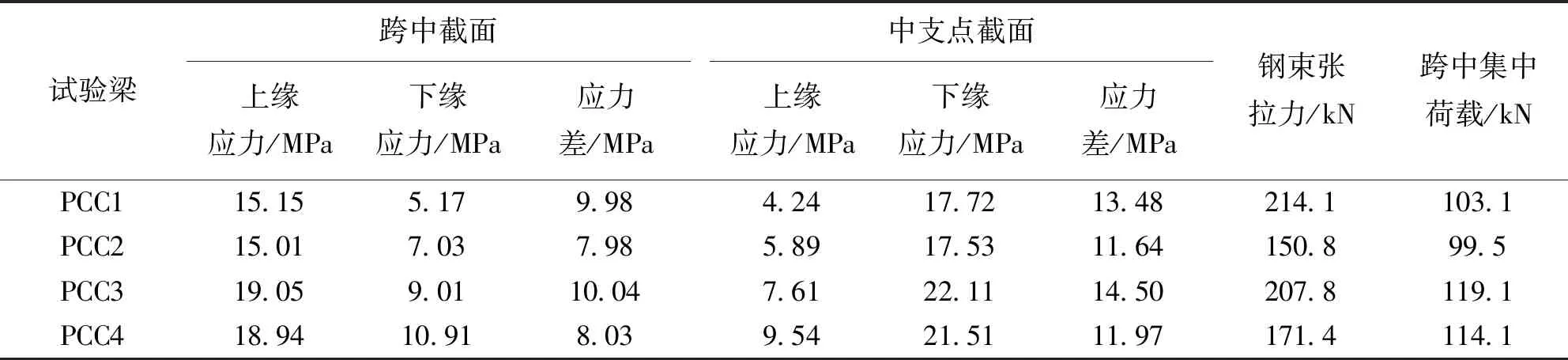
表1 各試驗梁關(guān)鍵截面初始應力狀態(tài)、單股預應力鋼束張拉力及跨中的集中荷載布置

1.2 試驗梁的加載方式

為了使試驗梁達到較高的應力狀態(tài)，同時避免加載系統(tǒng)出現(xiàn)卸載現(xiàn)象，試驗利用杠桿原理，通過地錨進行加載。如圖1所示，其中F1為壓重塊重量，F(xiàn)2為施加在試驗梁上的集中荷載，F(xiàn)3為固定端位置所承受的力。設計支座的加載裝置如圖2所示。根據(jù)杠桿原理可以得出施加在試驗梁跨中截面上緣的集中荷載F2的公式：

圖1 試驗梁加載

圖2 PC連續(xù)試驗梁加載裝置

1.3 試驗梁的測點布置

試驗中，應力是通過應變的測量來實現(xiàn)的，選取試驗梁跨中及中支點截面上、下緣布置應變傳感器。此外，為觀測試驗梁長期變形情況，選取跨中截面下緣布置位移測點，圖3所示為測點布置。

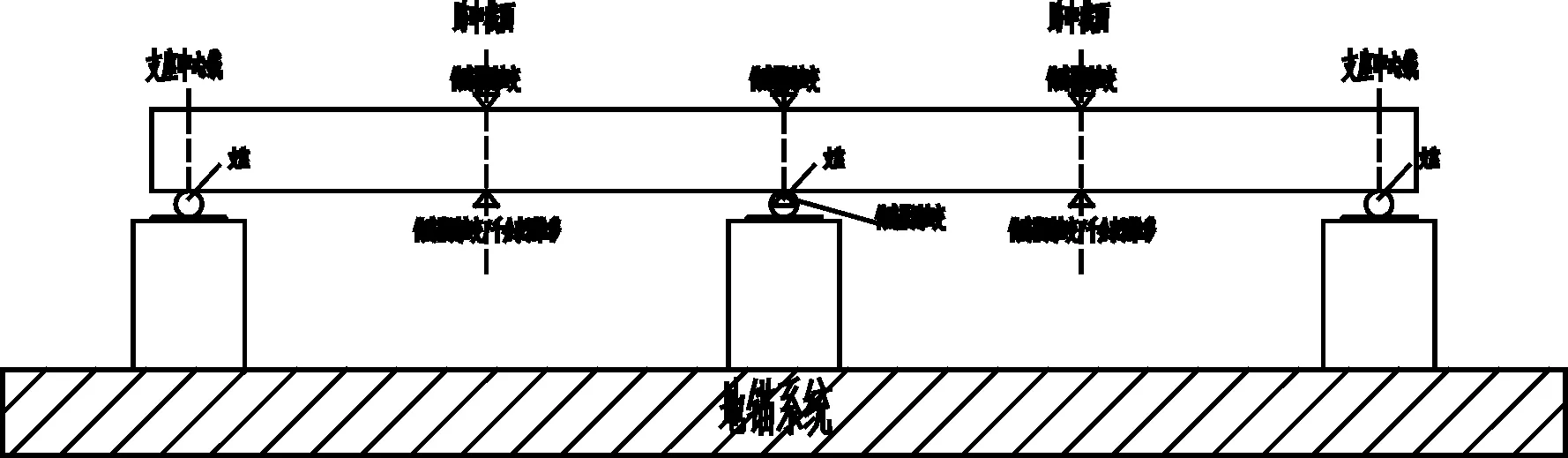
圖3 應變、位移測點布置

1.4 試驗加載流程

試驗前期準備工作完成后，即可布置數(shù)據(jù)采集系統(tǒng)、安裝加載設備，并進行初讀數(shù)。

初讀數(shù)完成后，采用預應力鋼束張拉和跨中集中荷載同時施加的方式對試驗梁進行加載，并分級逐步加載。施加跨中集中荷載時，試驗梁的兩跨應先后逐步施加。

試驗梁張拉加載前后，均需測定預應力錨固損失、錨固后預應力及1/4和3/4點處集中荷載、跨中及中支點截面上、下緣應力初始值，隨后定期采集上述數(shù)據(jù)，并進行分析。

2 試驗數(shù)據(jù)分析

2.1 預應力損失

后張法構(gòu)件傳力錨固后的預應力損失主要由預應力鋼束的應力松弛和梁體混凝土收縮徐變引起。通過壓力傳感器對試驗梁鋼束的預加力損失進行測定，鋼束的預加力隨時間的變化歷程如圖4所示。

圖4 預應力鋼束張拉力測試結(jié)果

從圖4可以看出：隨著時間的增加，鋼束的預加力不斷減小，前10d內(nèi)預加力損失較快，后期損失發(fā)展趨于平緩，這主要是由于前期鋼束的松弛及徐變效應發(fā)展較快引起的。相對于張拉錨固后的預加力大小，140d時的預應力損失分別為6.19%、7.83%、7.30%、7.04%。

表2列出了各試驗梁的預應力損失比例(相對于張拉錨固后的初始預應力大小)。可以看出：相對于140d時的預應力損失，20d的預應力損失分別達到了總預應力損失的62%，60d的預應力損失分別達到了總預應力損失的74%，100d的預應力損失分別達到了總預應力損失的88%。

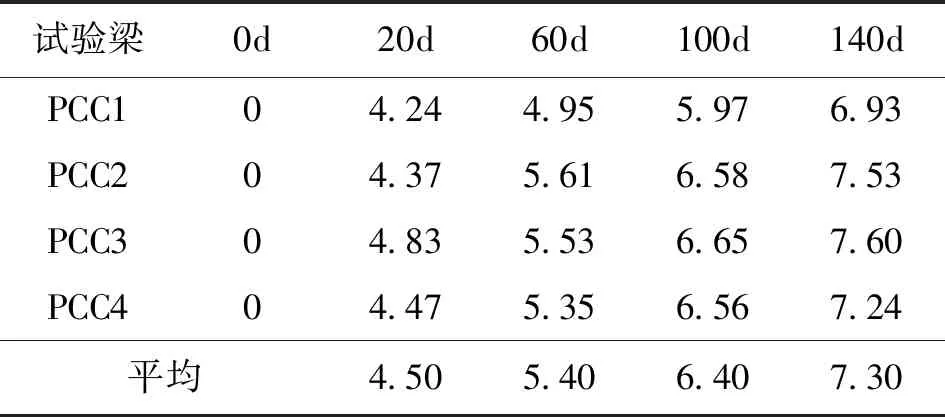
表2 連續(xù)試驗梁預應力損失比例 (單位：%)

通過與規(guī)范[11]計算值比較可知：各片連續(xù)試驗梁的實測預應力損失均較規(guī)范計算值大，張拉錨固后140d時，各片連續(xù)試驗梁預應力損失實測值與規(guī)范計算值的比值分別為1.25、1.20、1.17、1.22。

2.2 總應變與應力分析

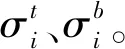
圖5 PCC1連續(xù)試驗梁應力與總應變變化時程

由圖5(a)可以看出，跨中截面上緣和中支點截面下緣的應力均隨著時間的發(fā)展不斷增加，且張拉錨固后前10d內(nèi)相對增加的速率較快，而10d后相對增加的速率趨于平緩；各試驗梁跨中截面下緣和中支點截面上緣的應力則呈現(xiàn)相反的變化趨勢，從而導致截面上、下緣的應力差不斷增加。由于結(jié)構(gòu)自重和外荷載未發(fā)生改變，產(chǎn)生這種截面應力變化的原因主要是由于鋼束預應力損失引起的。同時，預應力鋼束的松弛和混凝土徐變效應在試驗前期發(fā)展相對較快，從而導致跨中截面下緣應力及上、下緣應力差在試驗前期較快地發(fā)展。

對比總應變的變化時程可以看出，應力狀態(tài)越高，總應變變化就越明顯，而混凝土徐變產(chǎn)生的應變，不會導致應力的增加。

表3為張拉錨固后140d內(nèi)各連續(xù)試驗梁跨中截面上緣和中支點截面下緣總應變隨時間的增加值。可知：前期總應變增加較快，而隨著時間的發(fā)展總應變的增加趨于平緩；張拉錨固后30d時，各試驗梁跨中截面上緣的總應變增加值占140d內(nèi)該跨中截面上緣總應變增加值的比例分別為74.5%、68.5%、68.8%、68.5%;張拉錨固100d時，該比例分別為89.6%、87.9%、85.7%、85.3%；張拉錨固后30d時，各試驗梁中支點截面下緣的總應變增加值占140d內(nèi)該截面下緣總應變增加值的比例分別為69.7%、78.9%、73.5%、78.3%;張拉錨固100d時，該比例分別為91.3%、85.7%、89.0%、91.6%。

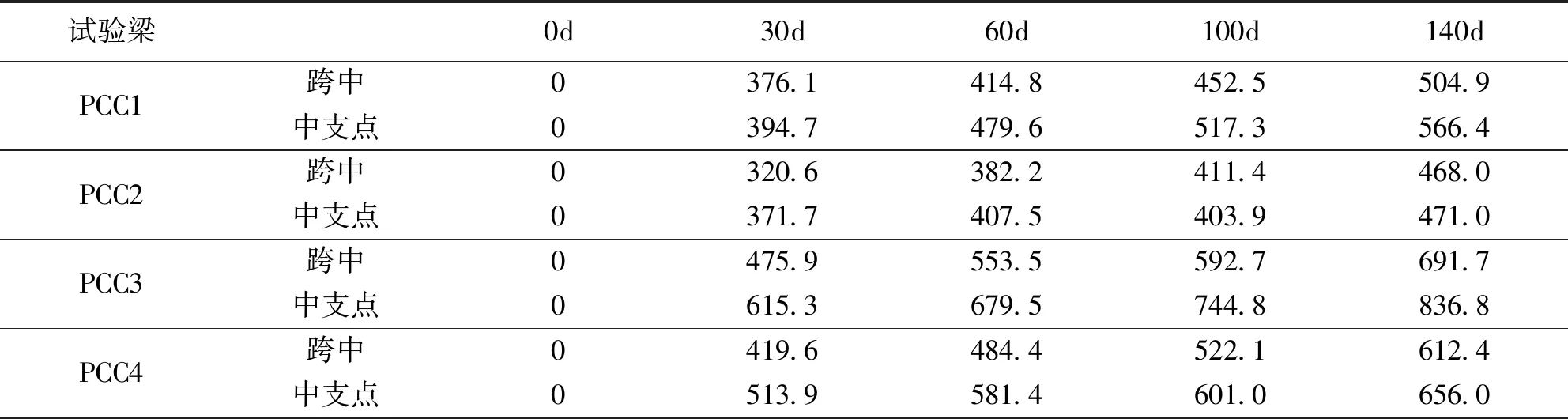
表3 連續(xù)試驗梁總應變增加值 (單位：με)

表4列出了各連續(xù)試驗梁跨中截面上緣與中支點截面下緣實測總應變與規(guī)范[11]計算值之間的差值。由表4可見，實測總應變均大于規(guī)范計算的總應變。

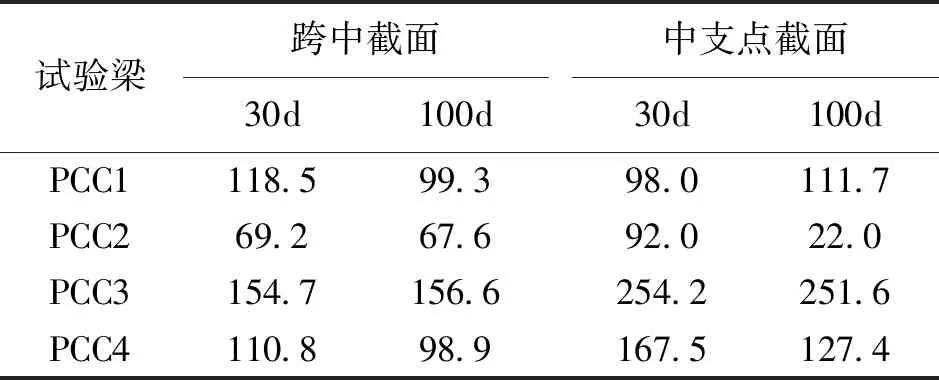
表4 連續(xù)試驗梁實測總應變與規(guī)范計算值的差值 (單位：με)

各試驗梁跨中截面上緣與中支點截面下緣實測總應變均較規(guī)范計算值大，主要是混凝土徐變應變的差異。

2.3 徐變應變分析

圖6為PCC1連續(xù)試驗梁跨中截面上緣及中支點截面下緣的徐變應變實測值與規(guī)范計算值之間的比較，其他試驗梁呈現(xiàn)出相似的變化規(guī)律。

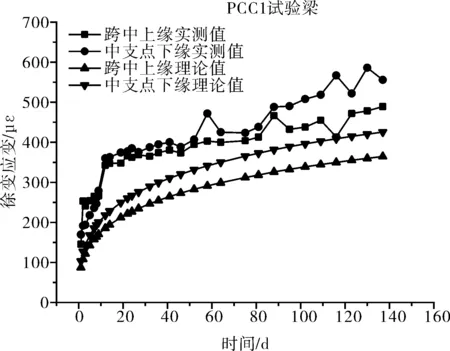
圖6 PCC1連續(xù)試驗梁實測徐變應變與規(guī)范計算值對比

從圖6可以看出：跨中截面上緣及中支點截面下緣的實測徐變應變與規(guī)范計算的徐變應變均隨著時間的發(fā)展不斷增加，且試驗前期徐變應變增加迅速，試驗后期徐變應變增加平緩；各連續(xù)試驗梁跨中截面上緣及中支點截面下緣的實測徐變應變均大于規(guī)范計算值；不同連續(xù)試驗梁間相同截面的徐變應變不同，主要是由于各試驗梁的應力水平不同所致，并且應力水平越高，上、下緣應力差越大，則該截面試驗梁的徐變應變越大。

表5列出了各試驗梁張拉錨固后不同時間段時跨中截面上緣及中支點截面下緣的實測徐變應變與規(guī)范計算值的比值，可以看出：各連續(xù)試驗梁跨中截面上緣及中支點截面下緣的實測徐變應變與規(guī)范徐變應變值的比值均大于1.00，可見現(xiàn)行規(guī)范考慮的徐變效應偏小，不能夠準確預測各試驗梁的實測徐變應變。

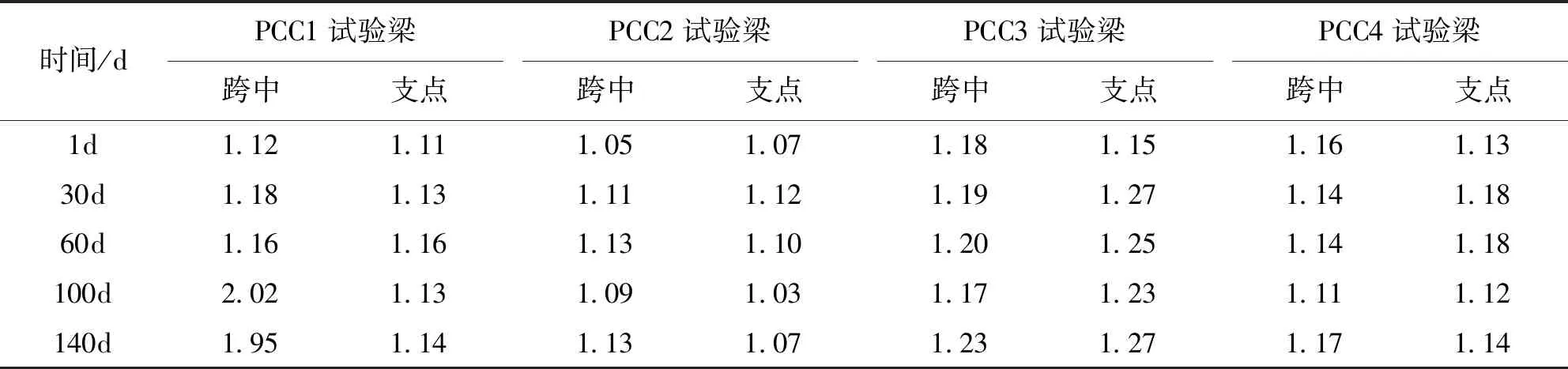
表5 試驗梁徐變應變實測值與規(guī)范計算值的比值

3 PC連續(xù)梁徐變與應力狀態(tài)的耦合作用

3.1 應力狀態(tài)對徐變的影響

通過試驗梁的徐變應變實測數(shù)據(jù)可知，混凝土徐變性能與試驗梁的應力狀態(tài)密切相關(guān)：試驗梁應力差保持基本相同時，徐變應變隨著應力水平的增大而增大；試驗梁應力水平保持基本相同時，徐變應變隨著應力差的增大而增大。而規(guī)范[11]中徐變計算考慮的因素包括混凝土加載齡期、混凝土強度、混凝土構(gòu)件理論厚度和年平均相對濕度。

任意時刻的徐變應變εcr和彈性應變εe，由徐變系數(shù)φ(t,t0)的定義，可得：

圖7為試驗梁跨中截面的實測徐變系數(shù)與規(guī)范徐變系數(shù)的比值。從圖7可見，實測徐變系數(shù)均大于規(guī)范的徐變系數(shù)，且跨中截面上緣應力水平越大，跨中截面上、下緣應力差越大，則實測徐變系數(shù)越大。

圖7 各試驗梁跨中截面實測徐變系數(shù)

3.2 基于實測數(shù)據(jù)的徐變系數(shù)修正

通過3.1節(jié)分析可知，實測總應變、徐變應變和預應力損失均大于規(guī)范計算值，主要是由于規(guī)范對于高應力狀態(tài)下混凝土徐變性能考慮不足導致。現(xiàn)行規(guī)范假定徐變系數(shù)與混凝土構(gòu)件的應力狀態(tài)無關(guān)，而試驗中通過實測徐變系數(shù)驗證了其與試驗梁的應力水平的相關(guān)性，且隨著試驗梁應力水平增大，試驗梁上、下緣應力差的增大，實測徐變徐系數(shù)與規(guī)范徐變系數(shù)的差值逐漸增大。因此，考慮修正衡量混凝土徐變性能的指標——徐變系數(shù)φ(t,t0)。

隨著時間的增加，各試驗梁的徐變系數(shù)均呈收斂趨勢。選擇指數(shù)函數(shù)和波爾茲曼函數(shù)對徐變系數(shù)進行修正，經(jīng)過多次擬合及試算，最終的修正系數(shù)λ與混凝土上緣壓應力σ以及時間t有關(guān)，如下式所示：

λ=f(σ,t)=[1.28+0.15e-0.09(t-t0)]·

式中:t為計算考慮時刻的混凝土齡期(d)；t0為加載時的混凝土齡期(d)；σ為試驗梁上緣的壓應力值(MPa)。

3.3 基于修正徐變系數(shù)的理論數(shù)據(jù)與實測數(shù)據(jù)的比較

3.3.1 徐變應變

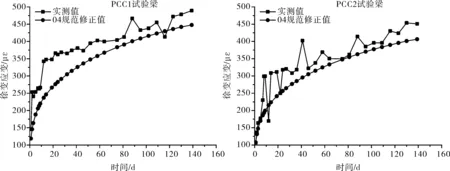
圖8 連續(xù)試驗梁跨中截面上緣實測與修正徐變應變

3.3.2 總應變

考慮修正系數(shù)λ后的總應變ε″計算公式：

ε″=εe+φ′(t,t0)·εe+εsh

圖9繪出了各連續(xù)試驗梁中支點截面下緣實測總應變ε′與考慮修正系數(shù)λ后的理論總應變ε″。從圖9可見，修正后的總應變與實測總應變隨時間的發(fā)展趨勢保持一致，修正后的總應變與實測總應變能較好地吻合。

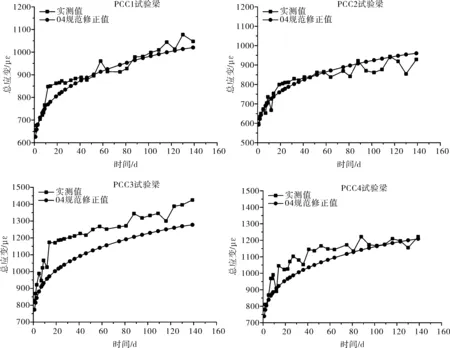
圖9 連續(xù)試驗梁中支點截面下緣實測與修正總應變

4 結(jié)論

針對影響預應力混凝土梁橋長期性能的各主要因素，包括混凝土的收縮、徐變特性以及預應力損失等，進行深入的試驗研究。通過對不同應力狀態(tài)下試驗梁的長期變形研究，為準確預測大跨徑預應力混凝土梁橋的長期變形提供試驗支持，得到以下結(jié)論：

(1)根據(jù)試驗數(shù)據(jù)，驗證了在高應力狀態(tài)下，結(jié)構(gòu)受壓總應變及徐變應變的實測值均大于規(guī)范計算值。當截面應力梯度(上、下緣應力差)保持基本相同時，預應力損失、受壓總應變及徐變應變隨著壓應力水平的增大而增大；當壓應力水平保持基本相同時，截面應力梯度越大跨中截面及中支點截面的上、下緣應力差越大則總應變及徐變應變越大。

(2)在高應力狀態(tài)下，實測徐變系數(shù)均大于規(guī)范給定的徐變系數(shù)，且隨著應力水平的提高，實測值與規(guī)范計算值差別越來越大，反映了混凝土徐變特性的非線性，應力水平越高，上、下緣應力差越大，則徐變系數(shù)越大。根據(jù)有限的試驗數(shù)據(jù)分析，得到了與應力狀態(tài)相關(guān)的徐變系數(shù)φ(t,t0)修正系數(shù)λ，考慮修正系數(shù)λ后的理論數(shù)據(jù)與試驗實測數(shù)據(jù)能較好地吻合，其準確性還需更多試驗進一步驗證。

(3)當應力水平σ/fck小于40%時，可采用規(guī)范推薦的線性徐變理論計算;而應力水平超過此范圍，則應充分考慮混凝土徐變的非線性。建議通過試驗得到高應力狀態(tài)下的混凝土徐變系數(shù)，從而更準確地預測預應力混凝土梁橋的長期變形和長期應力，保證橋梁的安全和正常使用性能。