波浪滑翔器柔性水翼推進性能數值仿真分析

劉 芬,彭 彬,孫秀軍,桑宏強,2

波浪滑翔器柔性水翼推進性能數值仿真分析

劉 芬1,彭 彬1,孫秀軍3,4*,桑宏強1,2

(1.天津工業大學機械工程學院,天津,300387; 2.天津市現代機電裝備技術重點實驗室,天津,300387; 3.中國海洋大學物理海洋教育部重點實驗室,山東 青島,266100; 4.青島海洋科學與技術試點國家實驗室,山東 青島,266237)

水翼是波浪滑翔器波浪動力轉換的關鍵部件,直接決定了波浪滑翔器的航行性能。文中研究了波浪滑翔器柔性水翼的推進性能,根據波浪滑翔器工作時水翼的運動特點,基于COMSOL Multiphysics軟件仿真出柔性水翼主動升沉運動下被動變形的過程,重點研究波浪參數、俯仰運動參數和斯特哈勞爾數對推進性能的影響。仿真結果表明,在一定范圍內,水翼推進性能隨波高、斯特哈勞爾數的增大而增大,隨波周期的增大而減小; 當波周期較大時,波高和波周期的變化對水翼推進性能的影響較小; 當俯仰周期與波周期相等時,俯仰運動對水翼推進性能有積極作用。文中結果可為波浪滑翔器被動柔性水翼后續研究提供參考。

波浪滑翔器; 柔性水翼; 推進性能; 數值仿真

0 引言

波浪滑翔器是一種新型海洋移動觀測平臺,可以將波浪能轉換為前向驅動動能,具有長期自主觀測能力,目前已廣泛應用于水文氣象數據觀測、環境監測、生物追蹤及遠程預警等領域[1-3]。

水翼作為決定波浪滑翔器波浪動力轉換的關鍵部件,國內外學者已經進行了大量研究。桑宏強等[4]通過仿真分析提出了振蕩水翼的最優運動方法,研究了水翼運動的極限位置等對波浪滑翔器推進速度的影響; 呂博元等[5]應用STAR-CCM+軟件對水翼的擺動進行仿真,研究了被動擺動、主動擺動、限位角及波浪參數等對水翼推進性能的影響,可知主動擺動的推進性能優于被動擺動,水翼推進性能受波浪參數影響較大,且隨波高和波浪頻率的增加而增加,在波浪頻率較小時,波浪頻率的變化對推進性能的影響較小; Liu等[6]對規則波作用下振蕩柔性水翼的推進性能進行了研究,可知在規則波波動頻率與水翼振蕩頻率相等的情況下,水翼的推進性能最佳; Liu等[7]針對后緣柔性的主動振蕩水翼能量汲取性能進行研究,發現水翼柔性激勵了前緣渦的產生,提升了能量汲取能力; Alben等[8]發現自主推進柔性體的推進速度存在共振峰值,提出理論模型,并通過了實驗驗證; Prempraneerach等[9]進行了二維柔性擺動水翼實驗,發現合理的弦向變形使得水翼效率提高了36%; Katz等[10]通過勢流理論分析得出,當柔性尾鰭具有弦向變形時,其推進效率比剛性尾鰭高; 田寶強等[11]在傳統波浪滑翔器的基礎上,引入了柔性蹼翼,搭建了原理樣機,通過水池實驗驗證了結構的可行性; 周凱[12]研究了典型仿生水翼的推進及能量吸收機制,結果表明對稱運動模式下水翼的推進性能隨斯特哈勞爾數的增大而增大,斯特哈勞爾數過大,會導致流場的不穩定。

文中在傳統波浪滑翔器的基礎上,引入柔性水翼進行研究,以期進一步提升波浪滑翔器的航行性能。根據波浪滑翔器及其水翼機構特殊的運動方式與特點,利用COMSOL Multiphysics軟件中的流體模塊、多體動力學模塊和多物理場耦合模塊,仿真柔性水翼隨波浪滑翔器運動過程中產生的升沉運動、俯仰運動及形變的耦合過程。研究運動參數對柔性水翼推進性能的影響,主要包括波浪參數、俯仰運動參數以及斯特哈勞數,可為柔性水翼的開發提供參考。

1 柔性水翼物理模型

1.1 工作原理

為進一步提升波浪滑翔器的航行性能,引入柔性水翼。柔性水翼在結構上與傳統波浪滑翔器的水翼機構有很大的差別,其主要通過在水動力下的彈性變形實現波浪能的吸收與利用。柔性水翼的優點主要表現在: 較剛性水翼結構更簡單,可靠性強; 較剛性水翼更易輕質,同等水動力條件下具有較小的慣性; 可綜合利用波浪滑翔器的升沉、俯仰和橫滾運動產生前向驅動力。

根據以往的實驗可知,波浪滑翔器在實際運動中的橫滾較小,一般不超過±5°,因此文中不考慮波浪滑翔器橫滾運動對柔性水翼的影響。假定波浪滑翔器以恒定的速度前向運動,當波峰來臨時,波浪滑翔器在波浪的作用下產生上升運動與俯仰運動,同時柔性水翼受水動力的作用沿中心線向下彎曲,與水流形成一定攻角,柔性水翼因此受到升力和阻力的共同作用而產生前向動力,進而作用于波浪滑翔器,如圖1(a)所示; 當波谷來臨時,波浪滑翔器在波浪的作用下產生下沉運動與俯仰運動,同時柔性水翼在水動力的作用下沿中心線向上彎曲,與水流形成一定的攻角,柔性水翼因此受到升力和阻力的共同作用產生前向運動,進而作用于波浪滑翔器,如圖1(b)所示。因此,柔性水翼在波浪中始終通過前向驅動力完成對滑翔機的推進。

1.2 運動規律

實際海況中,波浪形式非常復雜,導致水翼在波浪中的運動也極為復雜,通過數值仿真極難實現。為方便后續研究,結合線性波理論與柔性水翼的工作原理,對運動過程進行簡化,賦予柔性水翼升沉運動、俯仰運動以及流場作用下的變形,將波浪的運動、柔性水翼的升沉運動與俯仰運動均設定為正弦函數,具體表達式為

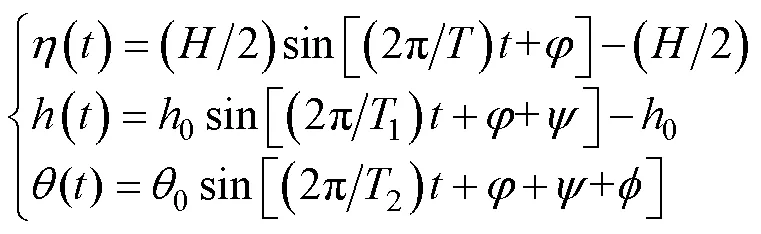
波浪滑翔器能夠充分利用波浪的起伏將水動力轉化為前向推力,在升沉方向具有良好的隨波性,因此認為波浪運動與柔性水翼升沉運動變化一致; 柔性水翼由初始狀態下沉時,在水動力的作用下,俯仰運動角由平衡位逐漸向負向增大; 翼前緣相對于波浪滑翔器是固定的,所以翼俯仰運動中心相對位置也是固定的,但為了后續研究的典型性,文中簡化翼前緣與俯仰運動中心一致。根據上述表述,可將式(1)中的參數設定為

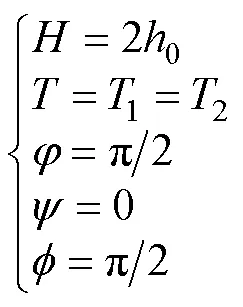
1.3 動力學參數

對于柔性水翼而言,無量綱參數斯特哈勞爾數對推進性能有很大的影響,且

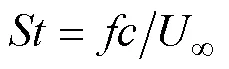
為更方便和直觀地衡量柔性水翼推進性能,將其在流場中前向方向的受力轉化為無量綱形式[5],推力系數為

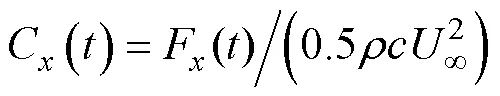
為更直觀地對比柔性水翼推進性能,計算得到1個周期內的平均推力系數[5]為

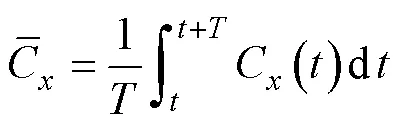
式中,為波周期。

2 仿真模型建立

2.1 計算模型

柔性水翼采用NACA0006翼型剖面,如圖2所示。文中取翼弦長度為180 mm,翼后緣長度C為140 mm,翼前緣長度C為40 mm。

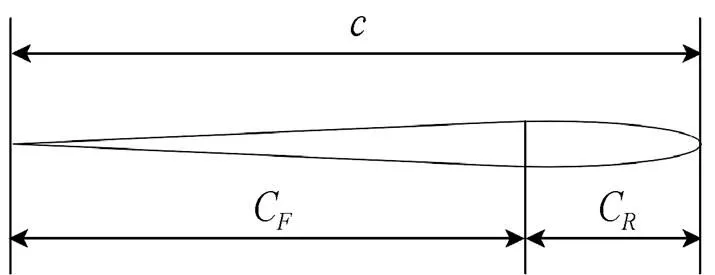
圖2 柔性水翼模型

翼后緣呈彈性,其柔度系數E[12]定義為

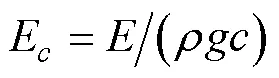
式中: 取E為5.7×103;為翼后緣的楊氏模量。

2.2 計算域及網格劃分

采用動網格技術研究柔性水翼在流場中的水動力特性。如圖3所示,柔性水翼的計算域為20×(+20),翼表面設置為無滑移邊界條件,其中心與計算域縱向中心線的距離為/2,與計算域橫向中心線重合,右側邊界設置為速度入口,左側邊界設置為壓力出口,上下邊界設置為壁面。為確保計算的準確性,翼表面增設大小為5×5的變形域,其中心與翼中心重合,變形域頂點與整體計算域頂點連線作輔助邊界。

采用湍流模型和COMSOL Multiphysics軟件對計算域進行非結構網格劃分,圖4為網格劃分示意圖。

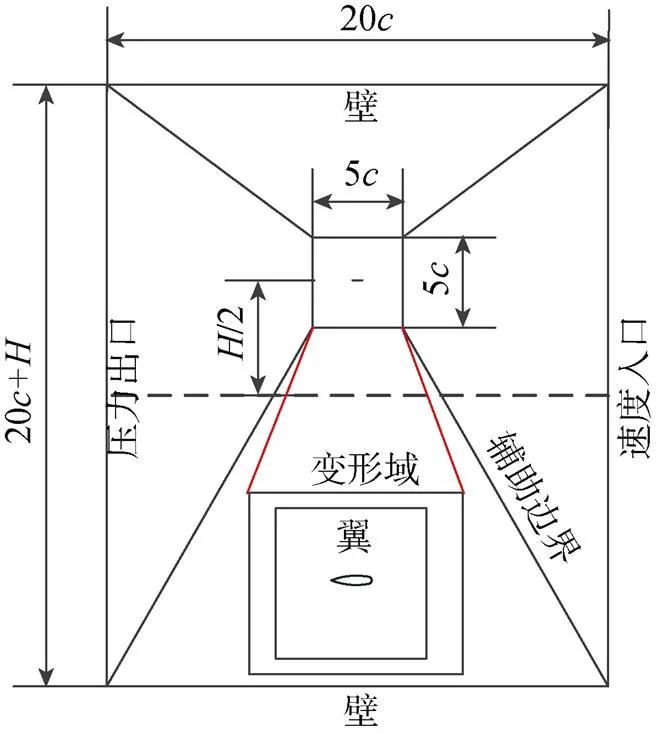
圖3 計算域及邊界條件示意圖

圖4 計算域網格劃分

2.3 模型驗證

為驗證所建立模型的準確性,對網格尺寸以及計算可靠性進行驗證。

2.3.1 網格無關驗證

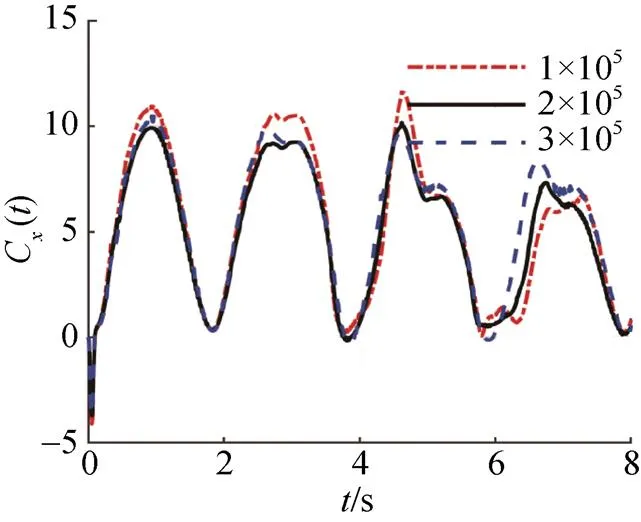
圖5 不同網格數量下翼推力系數變化曲線

2.3.2 可靠性驗證

表1 計算結果對比

3 仿真結果與分析

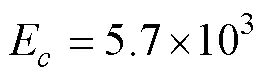
3.1 波浪參數對翼推進性能的影響

重點分析波高和波周期對翼推進性能的影響,其中波高為0.2～0.8 m,以0.2 m間隔選取,波周期為2～8 s,以2 s間隔選取,具體參數如表2所示。

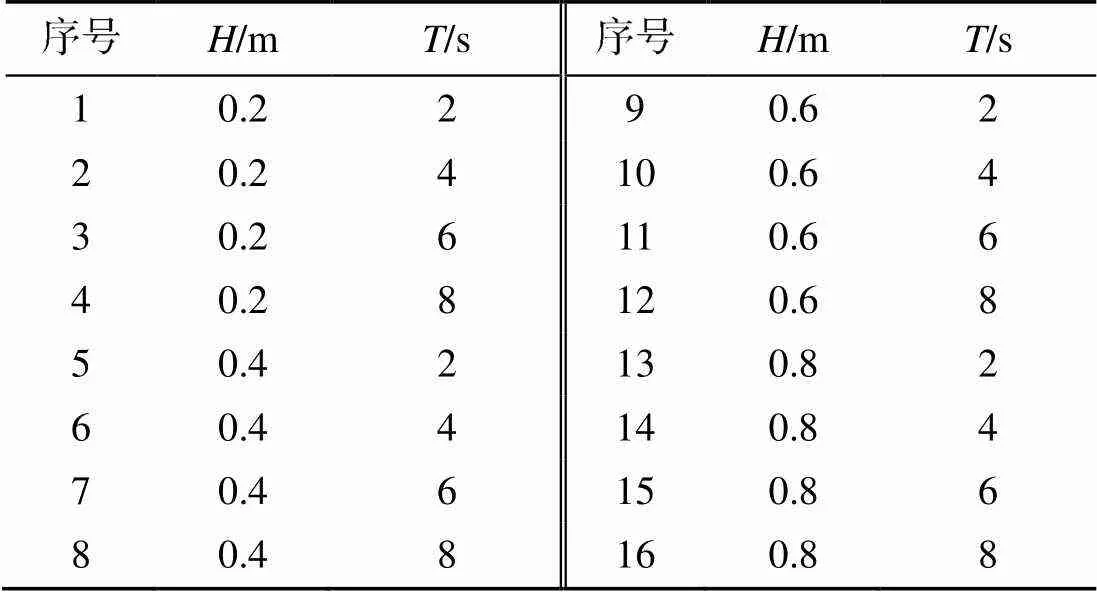
表2 數值仿真波浪參數

3.1.1 波高

圖6是波周期分別為=2,4 ,6,8 s時,不同波高下翼推力系數C()隨時間變化曲線。由于第1個周期處于啟動階段,流場處于不穩定狀態,而第2個周期穩定程度相對較好,因此選擇第2個周期進行分析。

由圖6(a)可知,推力系數隨波高的增大而增大,且在波高=0.4,0.6,0.8 m時,推力系數隨時間的變化波動較大,沒有呈現出明顯的周期性,說明柔性水翼運動中周圍的流場并未趨于穩定; 而在波高為0.2 m時,推力系數隨時間的變化明顯較小,且呈現出明顯的周期性。由此可知,當波周期=2 s時,較小的波高可使流場和推力系數趨于穩定,較大的波高會導致流場與推力系數的不穩定。

由圖6(b)～(d)可知,波周期=4,6,8 s時仍具有上述規律,且隨著波周期的增大,流場和推力系數在更大波高下穩定變化,其中: 波周期=4 s、波高=0.4 m; 波周期=6 s、波高=0.8 m; 波周期=8 s、波高=0.8 m時,推力系數趨于穩定。

筆者相信，以村落民俗志為基礎的鄉村研究，在當今中國重述“亞洲”、重寫“世界史”和“全球史”的學術熱潮中，不僅沒有過時，而且不可或缺。畢竟，體察中國國情，理解中國道路，提煉中國話語，仍要以“在村落里研究”[注][美]克利福德·格爾茨：《文化的解釋》，韓莉譯，譯林出版社，1999年，第29頁。 的鄉土中國學術實踐為立足點。

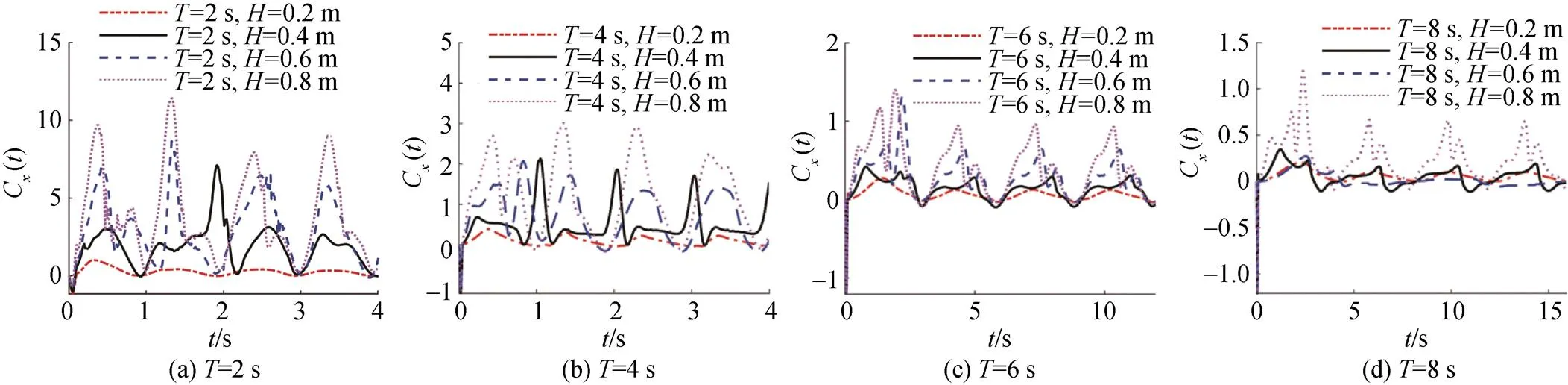
圖6 不同波高下翼推力系數隨時間變化曲線

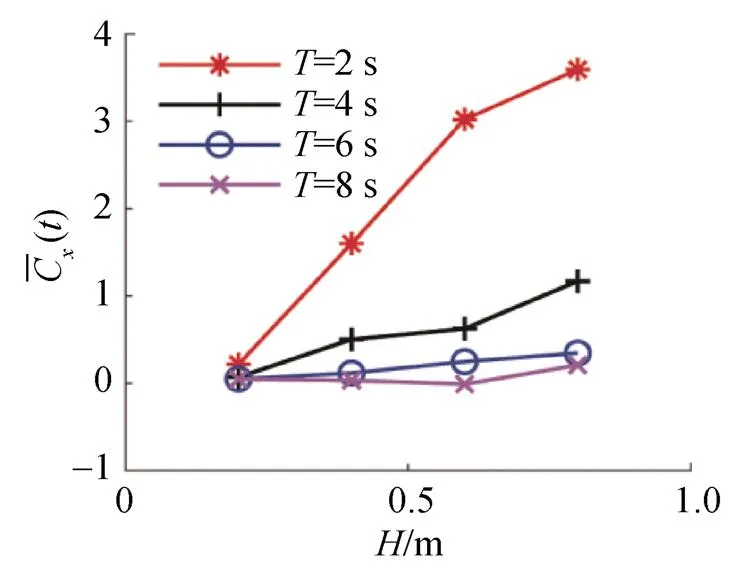
圖7 不同波高下翼平均推力系數變化曲線

3.1.2 波周期

圖8為翼推力系數在2個波周期隨時間變化的曲線,波高為=0.2,0.4,0.6,0.8 m。基于上節所述原因,選擇第2個周期進行分析。

由圖8(a)可知,推力系數隨波周期的增大而減小,且在波周期=4,6,8 s時,推力系數隨時間變化波動較小,呈現出明顯的周期性,流場趨于穩定,而在波周期=2 s時,推力系數隨時間的變化波動較大,沒有呈現出明顯的周期性,流場并未趨于穩定。可見,當波高為0.2 m時,較大的波周期可使流場和推力系數趨于穩定,較小的波周期會導致流場與推力系數的不穩定。

由圖8(b)～(d)可知,波高=0.4,0.6,0.8 m時仍具有上述規律,且隨著波高的增大,流場和推力系數在更大的波周期下穩定變化,其中波高=0.4 m、波周期=4 s,波高=0.6 m、波周期=4 s,波高=0.8 m、波周期=6 s時,推力系數趨于穩定。

圖9為不同波周期下柔性水翼平均推力系數的變化曲線。由圖可知,不同波高下,平均推力系數均隨波周期的增大而減小,且當波周期較小時,變化幅度較大,說明波周期對翼推進性能的影響程度較大; 波周期較大時,變化幅度較小,說明波周期的變化對翼推進性能的影響較小。該結果與文獻[5]相近。

3.2 俯仰運動參數對翼推進性能的影響

為分析俯仰運動參數對柔性水翼推進性能的影響,重點分析俯仰角幅值0和俯仰運動周期2對推進性能的影響,其中俯仰角幅值為0～15°,以5°間隔選取,俯仰運動周期為0～4 s,以2 s的間隔選取,設計的具體工況如表3所示。

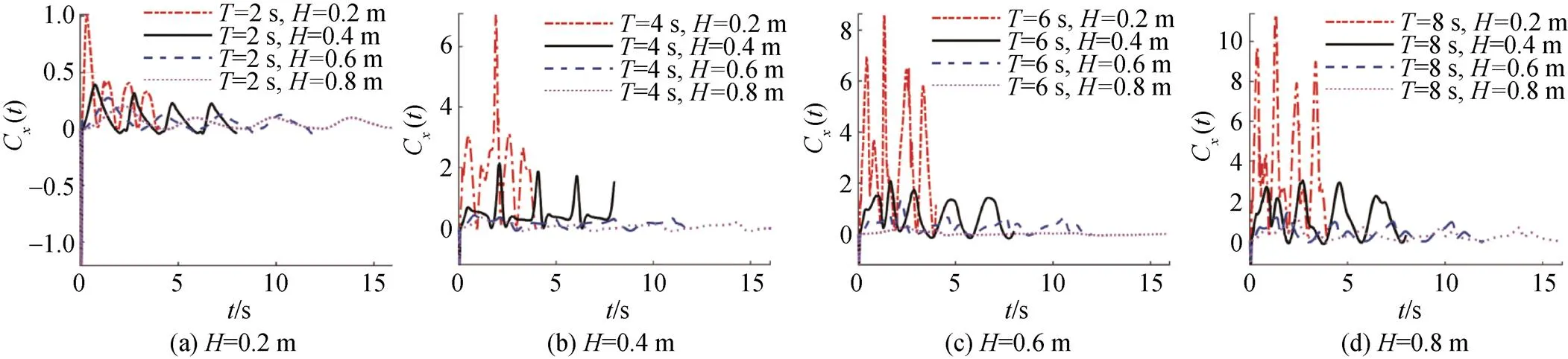
圖8 不同波周期下翼推力系數變化曲線

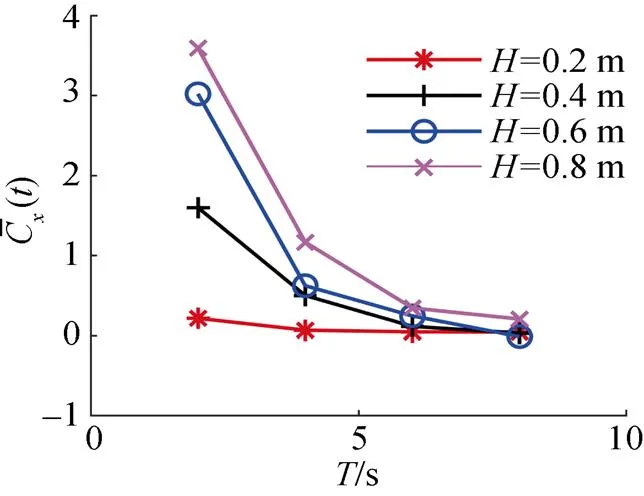
圖9 不同波周期下翼平均推力系數變化曲線

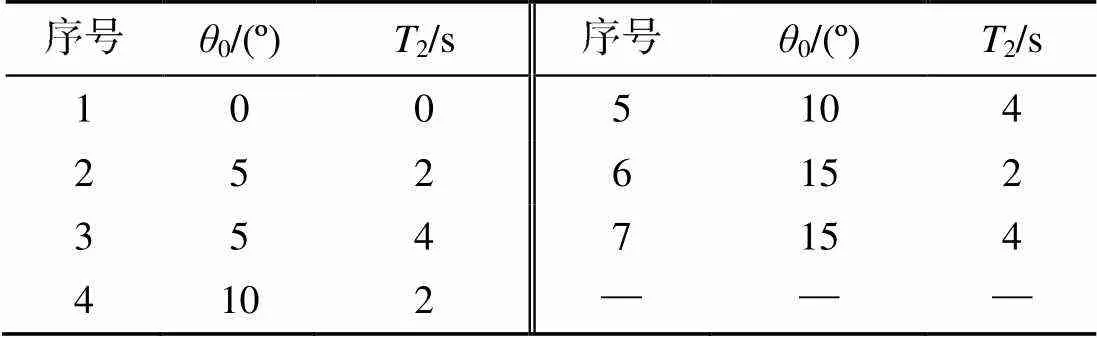
表3 數值仿真俯仰運動參數

3.2.1 俯仰角幅值

圖10為柔性水翼推力系數在俯仰運動周期2=2,4 s時隨時間變化的曲線,選擇計算中的第2個周期進行分析。由圖10(a)可知,在周期2=2 s時,隨俯仰角幅值的增大,推力系數出現負值的區域逐漸增大,隨時間變化的波動明顯增大,沒有呈現出明顯的周期性,流場并未趨于穩定; 由圖10(b)可知,在周期2=4 s時,隨俯仰角幅值的增大,推力系數呈現良好的周期性,流場均趨于穩定。

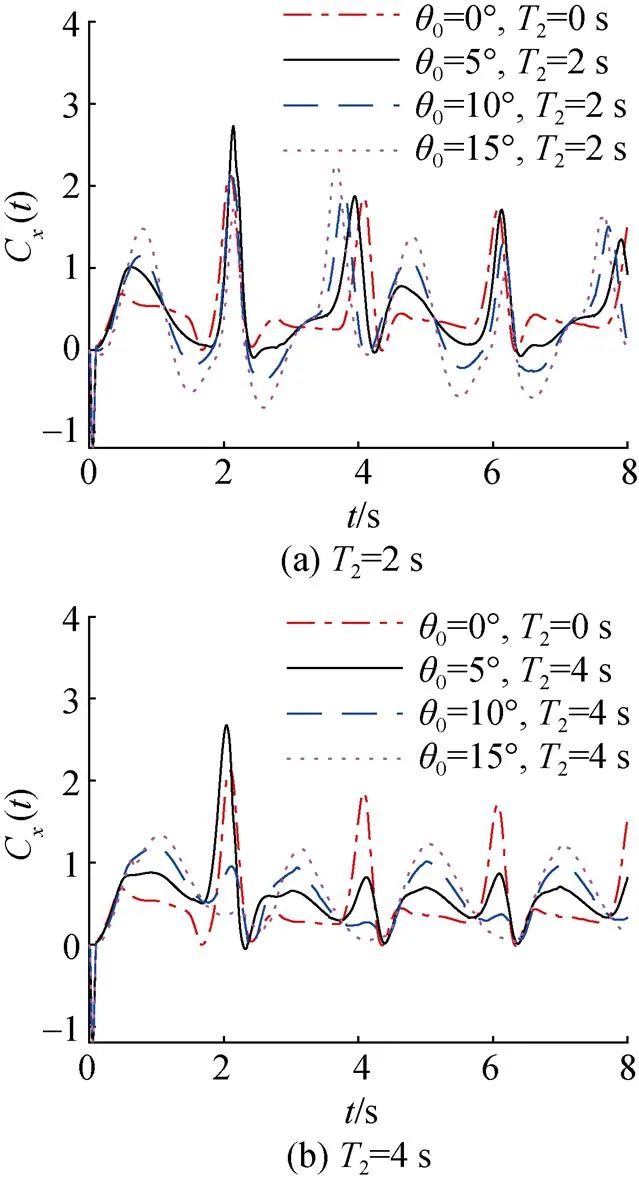
圖10 不同俯仰角幅值下翼推力系數變化曲線

圖11 不同俯仰角幅值下翼平均推力系數變化曲線

圖11中,當俯仰運動周期2與波周期相等時,俯仰角幅值在一定范圍內增大,平均推力系數隨之增大,變化幅度較小; 在俯仰運動周期為波周期的1/2時,平均推力系數隨俯仰角幅值的增大而減小,變化幅度較大。可見,當俯仰運動周期與波周期相等時,在一定范圍內,俯仰角幅值越大,推進性能越佳; 當俯仰運動周期為波周期的1/2時,在一定范圍內,俯仰角幅值越小,推進性能越佳。

3.2.2 俯仰運動周期

圖12為柔性水翼推力系數在2個波周期隨時間變化的曲線,俯仰角幅值0=5°,10°,15°時,選擇分析第2個周期。由圖可知,俯仰運動周期的減小使得推力系數隨著時間變化的波動明顯增大,且周期性明顯變差,流場由較穩定向較不穩定轉變。

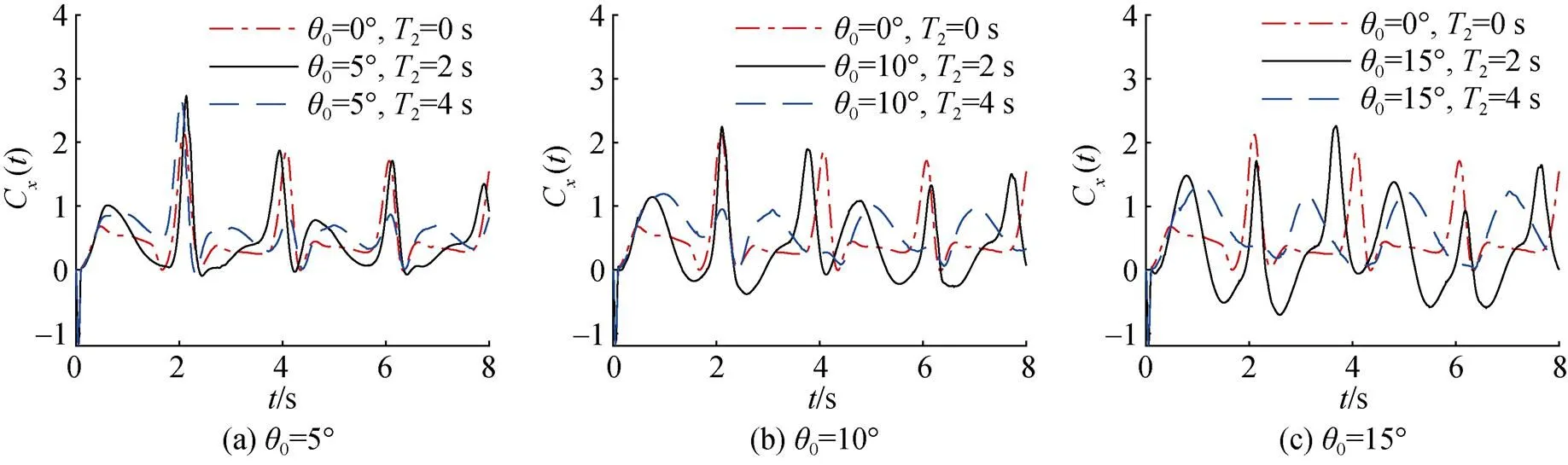
圖12 不同俯仰運動周期下翼推力系數變化曲線

圖13為不同俯仰運動周期下柔性水翼的平均推力系數變化曲線,由圖可知,平均推力系數均隨俯仰運動周期的增大呈先減小后增大的趨勢,且在俯仰角幅值較小時,俯仰運動周期對平均推力系數的影響較小。

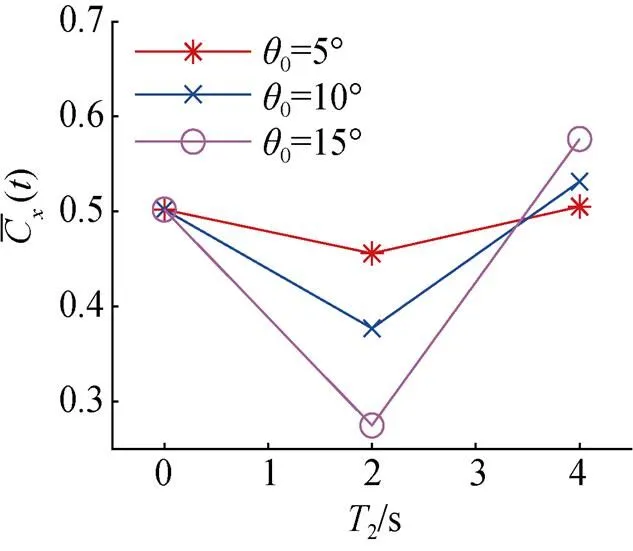
圖13 不同俯仰運動周期下翼平均推力系數變化曲線

3.3 斯特哈勞爾數對翼推進性能的影響

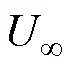
圖14為柔性水翼推力系數在2個波周期內隨時間變化曲線,斯特哈勞爾數=0.450,0.225,0.150,0.1125,0.090,選擇計算中的第2個周期進行分析。

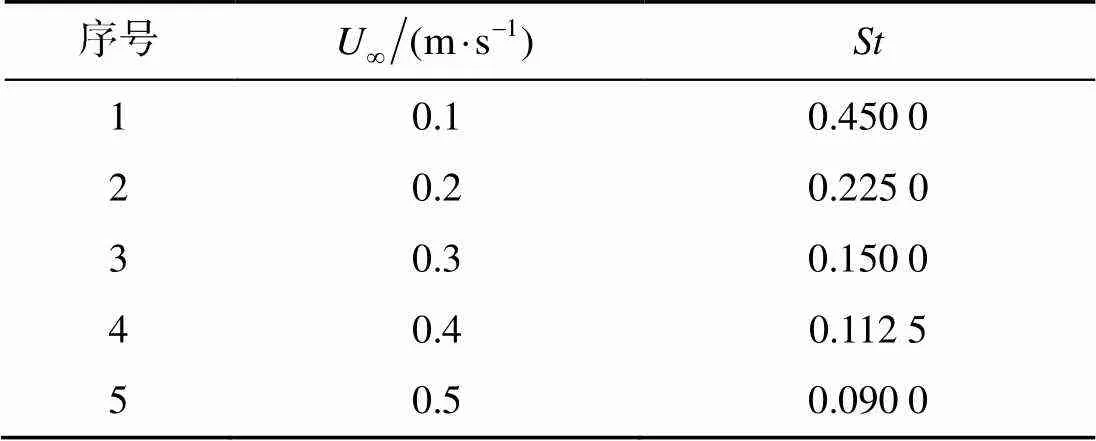
表4 數值仿真斯特哈勞爾數

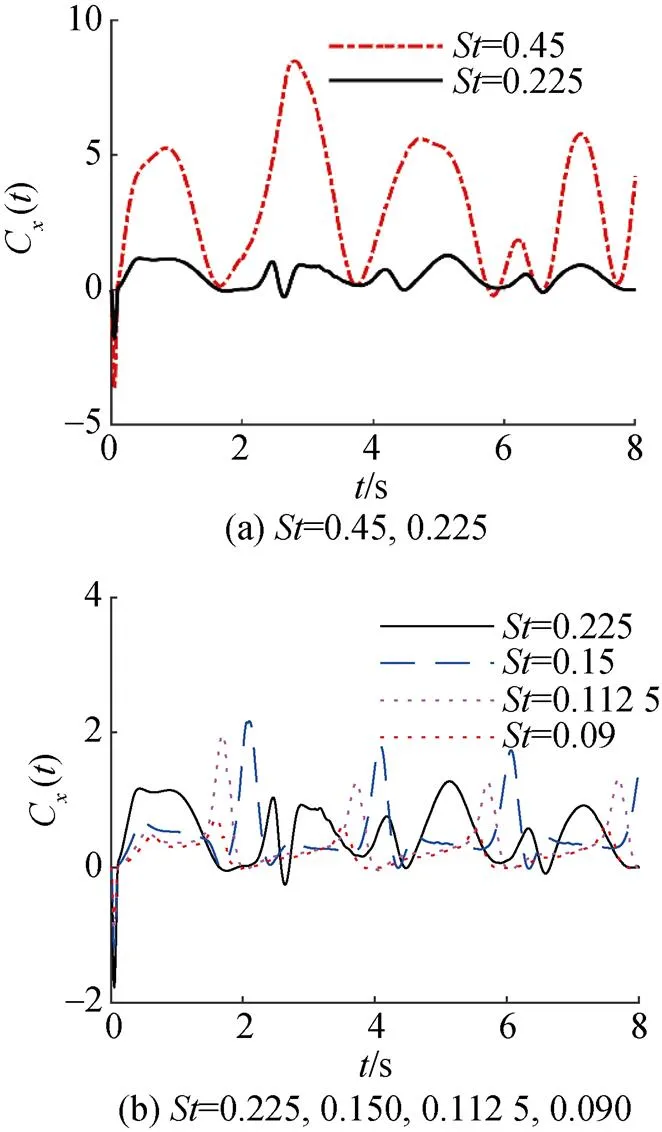
圖14 不同斯特哈勞爾數下翼推力系數變化曲線

由圖可知,隨著斯特哈勞爾數的減小,推力系數隨時間變化的波動明顯減小,流場逐漸趨于穩定,呈現出明顯的周期性,且當斯特哈勞爾數較小時,對推力系數的影響較小。

圖15為不同斯特哈勞爾數下柔性水翼的平均推力系數變化曲線,由圖可知,平均推力系數基本符合隨斯特哈勞爾數增大而增大,斯特哈勞爾數較小時,其改變對平均推力系數的影響較小,該結果與文獻[12]研究結果相近。

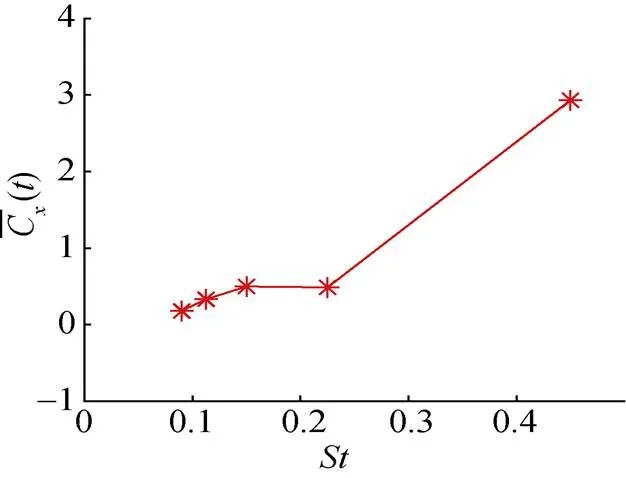
圖15 不同斯特哈勞爾數下翼平均推力系數變化曲線

4 水池實驗驗證

4.1 實驗平臺搭建

水翼推進實驗平臺能夠實現柔性水翼的升沉振蕩運動,使得柔性水翼在流場作用下產生形變,從而產生前向推力。實驗平臺主要由氣動裝置、主體框架、滑動導軌、拉力測試儀和柔性水翼機構組成,通過調節氣動裝置的氣壓來調節柔性水翼升沉運動的行程和周期,主體框架搭載氣動裝置和柔性水翼機構,在與柔性水翼前向相反的方向安裝拉力測試儀,實時接收柔性水翼機構的前向推力數據,實驗平臺如圖16所示。

圖16 實驗平臺

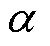
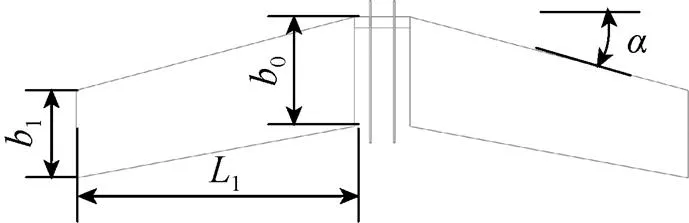
圖17 柔性水翼幾何參數

圖18 柔性水翼實物圖

4.2 實驗結果分析

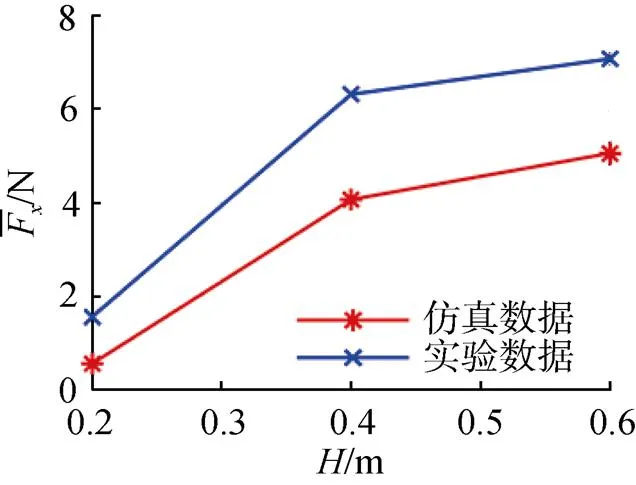
圖19 波周期T=4 s下仿真與實驗平均推力對比曲線

盡管存在一定偏差,但仿真數據與實驗數據趨勢性一致,符合前文仿真分析得出的規律,水池實驗在一定程度上驗證了文中的仿真結果。

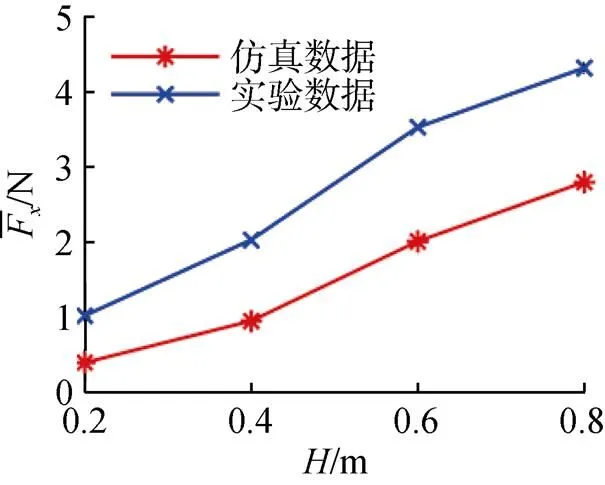
圖20 波周期T=6 s下仿真與實驗平均推力對比曲線

5 結論

文中以波浪滑翔器中的柔性水翼為研究對象,對柔性水翼在波浪中的運動進行仿真分析,重點分析了運動參數對翼推進性能的影響,得到如下結論: 1) 通過COMSOL Multiphysics軟件的流體場與固體場相結合的模型,實現了柔性水翼在升沉運動和俯仰運動耦合中產生被動變形的仿真; 2) 在一定范圍內,翼推進性能隨波高的增大而增大,且較大的波高易導致翼周圍的流場不穩定,當波周期較大時,波高對翼推進性能的影響較小; 3) 在一定范圍內,翼推進性能隨波周期的增大而減小,較小的波周期易導致翼周圍流場不穩定,對翼推進性能的影響較大; 4) 在一定范圍內,當俯仰運動周期與波周期相等時,俯仰運動對翼推進性能有積極作用,且俯仰角幅值越大,翼推進性能越佳,當俯仰運動周期與波周期不相等時,俯仰運動對翼推進性能有消極作用,且俯仰角幅值越小,翼推進性能越佳; 5) 在一定范圍內,翼推進性能隨斯特哈勞爾數的減小而減小,且在低斯特哈勞爾數下對翼推進性能影響較小; 6) 仿真數據和實驗數據存在一定偏差,但二者趨勢性相近,一定程度上驗證了文中的仿真結果。

[1] Daniel T,Manley J,Trenaman N. The Wave Glider: Enabling a New Approach to Persistent Ocean Observation and Research[J]. Ocean Dynamics,2011,61(10): 1509-1520.

[2] Hine R,Willcox S,Hine G,et al. The Wave Glider: A Wave-Powered Autonomous Marine Vehicle[C]//Procee- dings of MTS/IEEE Biloxi-Marine Technology for Our Future: Global and Local Challenges. Biloxi,USA: IEEE,2009: 296-301.

[3] 廖煜雷,李曄,劉濤,等. 波浪滑翔器技術的回顧與展望[J]. 哈爾濱工程大學學報,2016,37(9): 1227-1236.

Liao Yu-lei,Li Ye,Liu Tao,et al. Unmanned Wave Glider Technology: State of Art and Perspective[J]. Journal of Harbin Engineering University,2016,37(9): 1227-1236.

[4] 桑宏強,李燦,孫秀軍. 波浪滑翔器縱向速度與波浪參數定量分析[J]. 水下無人系統學報,2018,26(1): 16-22.

Sang Hong-qiang,Li Can,Sun Xiu-jun. Quantitative Analysis on Longitudinal Velocity and Wave Parameter of Wave Glider[J]. Journal of Unmanned Undersea Systems,2018,26(1): 16-22.

[5] 呂元博,田新亮,李欣,等. NACA 0012擺動撲翼水動力特性的二維數值模擬[J]. 中國艦船研究,2018,13(2): 7-15.

Lü Yuan-bo,Tian Xin-liang,Li Xin,et al. Two-dimen- sional Numerical Simulation of NACA 0012 Flapping Foil Hydrodynamics[J]. Chinese Journal of Ship Research,2018,13(2): 7-15.

[6] Liu P,Liu Y B,Huang S L,et al. Effects of Regular Waves on Propulsion Performance of Flexible Flapping Foil[J]. Applied Sciences,2018,8(6): 934.

[7] Liu W,Xiao Q,Zhu Q. Passive Flexibility Effect on Oscillating Foil Energy Harvester[J]. AIAA Journal,2016,54(4): 1-16.

[8] Alben S,Witt C,Baker T V,et al. Dynamics of Freely Swimming Flexible Foils[J]. Physics of Fluids,2012,24(5): 109-133.

[9] Prempraneerach P,Hober F S,Triantfyllou M S. The Effect of Chordwise Flexibility on the Trust and Efficiency of a Flapping foil[C]//Proceedings of the 13th International Symposium on Unmanned Untethered Submersible Technology. Durham,USA: IEEE,2003: 130-128.

[10] Katz J,Weihs D. Hydrodynamic Propulsion by Large Amplitude Oscillation of an Airfoil with Chordwise Flexibility[J]. Journal of Fluid Mechanics,1978,88(3): 485-497.

[11] 田寶強,李玲瓏. 蹼翼型波浪滑翔機結構設計和運動原理分析[J]. 中國機械工程,2017,28(24): 2939-2943.

Tian Bao-qiang,Li Ling-long. Structure Design and Movement Principle of Wave Gliders with Webbed Wings[J]. China Mechanical Engineering,2017,28(24): 2939-2943.

[12] 周凱. 典型仿生水翼的推進及能量吸收機制研究[D]. 哈爾濱: 哈爾濱工程大學,2018.

[13] Kinsey T,Dumas G. Computational Fluid Dynamics Analysis of a Hydrokinetic Turbine Based on Oscillating Hydrofoils[J]. Journal of Fluids Engineering,2012,134(2): 021104.

Numerical Simulation Analysis of Flexible Hydrofoil Propulsion Performance for Wave Glider

1,1,3,4*,1,2

(1. School of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387,China; 2.Tianjin Key Laboratory of Advanced Mechatronic Equipment Technology,Tianjin 30087,China; 3. Physical Oceanorgraphy Laboratory,Ocean University of China,Qingdao 266100,China; 4. Laboratory of Marine Dynamics and Climate Function,Pilot National Laboratory for Marine Science and Technology(Qingdao),Qingdao 266237,China)

The hydrofoil is a key component that determines the capability of wave power conversions and the navigation performance of wave gliders. The propulsion performance of a flexible hydrofoil is investigated in this study. The passive deformation process of a flexible hydrofoil under active heave motion is simulated using the COMSOL Multiphysics software according to the motion characteristics of a hydrofoil when the wave glider is working. The effects of wave and pitching motion parameters and the Strouhal number on the propulsion performance of the hydrofoil are investigated. The simulation results show that the propulsion performance of the hydrofoil increases with wave height and Strouhal number and decreases with wave period within a certain range. When the wave period is high,the change in wave height and wave period has little effect on the propulsion performance of the hydrofoil. In contrast,when the pitch and wave periods are equal,the pitching motion has a positive effect on the performance.

wave glider; flexible hydrofoil; propulsion performance; numerical simulation

TJ630; U674.941; O353

A

2096-3920(2021)04-0374-09

10.11993/j.issn.2096-3920.2021.04.002

劉芬,彭彬,孫秀軍,等. 波浪滑翔器柔性水翼推進性能數值仿真分析[J]. 水下無人系統學報,2021,29(4): 374-382.

2020-08-28;

2020-11-11.

山東省重大科技創新項目(2019JZZY020701);天津市自然科學基金重點基金(18JCZDJC40100); 國家重點研發計劃重點專項(2017YFC0305902); 青島海洋科學與技術國家實驗室“問海計劃”項目(2017WHZZB0101).

通信作者簡介:孫秀軍(1981-),男,博士,教授,主要研究方向為波浪滑翔器技術及其海洋觀測應用.

(責任編輯: 楊力軍)