基于偏離度優化的高速列車軸箱軸承溫度預測方法*

孟建軍 潘彥龍 陳曉強 李德倉 胥如迅

(①蘭州交通大學機電技術研究所,甘肅 蘭州730070；②甘肅省物流及運輸裝備信息化工程技術研究中心,甘肅 蘭州 730070；③蘭州交通大學機電工程學院,甘肅 蘭州 730070；)

轉向架上軸箱、齒輪箱、電機等重要位置都分布有軸承，在確保列車運行安全方面，軸承是不可或缺的[1]。

列車運行中軸承異常溫升是危及鐵路運輸安全的嚴重故障，輕則造成緊急停車引起經濟損失，重則可能引發列車脫軌危及旅客生命安全[2]。溫度可以直接反應軸承的工作狀態，溫度的異常是軸承發生故障的重要信號。現有車載軸溫監測系統可以對軸溫進行實時監測，通過設定的閾值來對軸溫進行預警。但是一旦發生報警，必須立即進行處理，留給相關人員的處理時間少。因此，通過對高速列車的軸溫進行預測追蹤，提前掌握下一時段軸溫的變化趨勢，為處理軸溫異常預留足夠時間，對高速列車預警及調整行車策略有重要的工程價值[3]。

針對溫度的預測研究，Qiu Rujian等采用長短期記憶網絡對河流日水溫進行預測[4]。張恒志等根據車載系統收集的走行部數據是多維時間序列的特點，提出一種基于稀疏注意力機制的城軌車輛軸溫預測模型[5]。宋佳音采用加權混合法和卡爾曼融合算法對ARIMA模型和PSO-SVM模型進行了融合分析[6]。張繼冬等建立了基于服役工況參數的SVM軸承溫度預測模型[7]。梁濤等基于灰色關聯度理論提出變權組合方法對齒輪箱溫度進行預測[8]。Hrachya Astsatryan等通過氣象臺站收集的觀測數據，用基于機器學習的方法對亞美尼亞地區氣溫進行預測[9]。尹艷松等采用非線性狀態估計(NSET)的方法對軸承溫度進行預測研究[10]。葉鈺等提出無線通信的正交試驗方法來分析耦合因素對高速電主軸的熱誤差作用[11]。

目前對軸溫進行提前追蹤預測的研究較少，在列車上軸溫測點較多，各種軸承之間的工況差異較大，并且熱軸故障是鐵路運營單位極力避免的重大故障，發生次數較少。列車軸溫數據采集頻率低且引起軸溫升高的因素多樣，在僅知道溫度的前提下為灰色系統。因灰色理論具有建模樣本少，精度較高的優點，利用灰色理論對軸溫進行預測可以有效解決數據量少的問題。

1 基于灰色理論的列車軸溫預測模型參數優選

在用灰色理論建模對軸溫進行預測時，除了選擇軸溫序列外，對于模型的建模數、預測的步長這3個參數進行闡述說明。并通過分析統計結果，對建模參數及迭代數進行選擇。

1.1 建模參數說明

1.1.1預測數

預測數即預測步長，使用前mmin分鐘的歷史軸溫數據預測后續nmin分鐘的軸溫數據。建立模型前，需要對軸溫預測步長進行選擇。預測步長過大模型預測精度將降低，預測步長過小則會造成不能滿足實際需要。

1.1.2建模數

本文引用文獻[3]建模數的概念，用建模數代指構建模型所需要的數據點個數。在用灰色理論進行軸溫預測時，選擇不同的建模數會影響模型的精度。建模數過少則不能反映軸溫變化的整體規律，造成模型的精度下降。建模數過多，不僅會造成模型的計算效率降低，由于包括的陳舊信息過多，造成信息冗余，不能將軸溫最新的發展趨勢展示出來。因而需要根據實際需要選擇合理的建模數。

1.1.3預處理參數

本文研究車載軸溫監測系統所用的溫度傳感器為pt100，采樣頻率為1/60 Hz，采樣精度為1 ℃。軸溫數據每分鐘傳輸一次且為整數。由于采集到的原始軸溫監測數據質量較差，存在缺失、重復、階躍等問題，因而需要對傳感器采集到的軸溫數據進行預處理。對軸溫監測數據中的跳變點進行刪除處理，對溫度缺失值插值處理，對溫度信號平滑處理以提高模型的精度。因曲線擬合方法會由于核函數選擇的不同，導致軸溫的變化情況呈現核函數的溫升規律，不能正確反映原始軸溫的溫升規律。選用滑動平均處理的方式則不會對原始數據變化規律造成影響。

設選取的原始軸溫數據為X=[x1,x2,…,xn]，則經過滑動處理后的數據為X(0)為：

(1)

滑動處理的數據可以重復進行相同的處理，重復處理數據的次數為迭代次數。適當的迭代次數可以提高數據的平滑度進而保證模型的精度，但是迭代次數過多，數據會過于平滑而失真，使得不能正確反映溫升規律，造成模型的準確度下降。

1.2 建模參數選擇

通過查閱相關資料，預測時間越長，則模型的預測精度會得不到保證。選擇5 min的短時預測，便可滿足車輛實際運營時的軸溫預測需求[12]。因而本文選擇預測數為5。

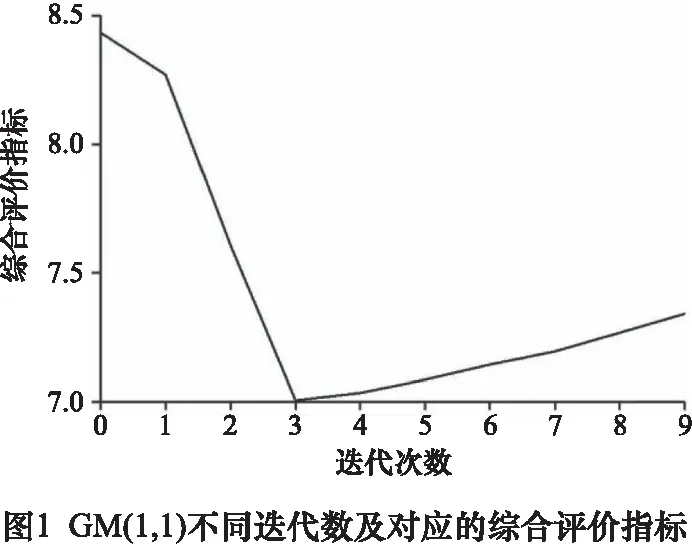
為選擇合適的迭代數及建模數，對某型高速列車的歷史軸溫數據進行預測，將最大絕對誤差與平均絕對誤差的和作為綜合評價指標。對不同迭代數對應的綜合評價指標進行統計，結果如圖1所示。

由圖1可以看出迭代數為3時，綜合評價指標最小，模型的性能更佳。在選定迭代數為3的情況下，對不同建模數進行綜合評價指標統計，如圖2所示，得出建模數一般選6～8為宜。

2 基于灰色二次回歸的軸溫預測模型

2.1 基于GM(1,1)的軸溫預測模型

設序列X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]，其中x(0)(k)≥0,k=1,2,...，n;X(1)序列為X(0)序列的1-AGO序列[13]：

X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]

(2)

其中：

(3)

Z(1)=[z(1)(2),z(1)(3),…,z(1)(n)]

(4)

(5)

則GM(1,1)模型為[14]：

x(0)(k)+az(1)(k)=b

(6)

其中a為發展系數，b為灰作用量。

(7)

其中：

(8)

GM(1,1)模型的解：

(9)

最終GM(1,1)模型求得的預測值為：

(10)

2.2 基于灰色二次回歸的軸溫預測模型

灰色二次回歸模型是將二次多項式與GM(1,1)模型融合，使用最小二乘法求解模型的參數，從而確定模型。

GM(1,1)模型的解可記為：

(11)

基于灰色二次回歸的時序預測模型則使用指數方程Y=aebx和二次多項式方程Y=aX2+bX來擬合x(1)(i)，記作：

(12)

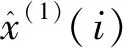
其中參數v由GM(1,1)模型計算得出a后，使得v=-a，C1、C2、C3和C4則通過使用最小二乘法得出，求解方法為：

(13)

(14)

GM(1,1)的解為指數形式的，因此GM(1,1)實質是指數的擬合模型。在使用GM(1,1)模型對接近指數上升的單調變化的曲線進行擬合時效果較好，但是對凹凸變化的曲線擬合的誤差較大。

2.3 軸溫波動序列測試結果

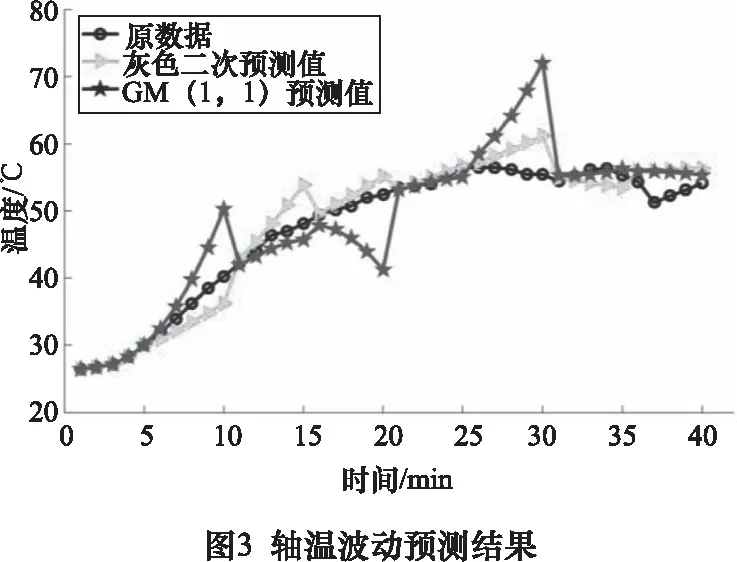
以一段高速列車實際軸溫波動數據為例，采用灰色二次回歸預測模型與GM(1,1)模型進行預測，如圖3所示。結果顯示，灰色二次回歸模型跟實際軸溫的擬合較好。由于GM(1,1)具有指數增長的性質，因而在軸溫預測時會出現預測值比實際值偏高的現象，灰色二次多形式是對GM(1,1)模型的改進，可以在一定程度上規避這一現象。

同理，用兩種模型對軸溫曲線進行擬合預測時，GM(1,1)模型由于其特有的屬性，其對單調變化的曲線有更好的擬合，灰色二次回歸模型對凹凸變化的軸溫曲線有較好的擬合能力。

3 基于偏離度的灰色二次回歸與GM(1,1)組合預測模型

3.1 模型構建

選擇相對鄰近的歷史軸溫數據，建立預測模型對軸溫進行短時預測。當軸溫達到最小建模的數據量，利用模型預測未來n分鐘的溫度，每n分鐘對輸入模型的軸溫數據進行更新。并重新根據更新的數據建立模型，預測下一個n分鐘的軸溫。當用第i個預測模型時，前一個預測模型與實測值的偏差變成已知。根據第(i-1)個GM(1,1)模型與灰色二次回歸預測的偏差確定權值w1、w2，以此來修正誤差。在(t-n)時GM(1,1)與灰色二次回歸模型預測后n分鐘輸出軸溫和實測軸溫為：

(15)

式中:PGM(1,1)為GM(1,1)預測輸出序列。

(16)

式中:P灰為灰色二次回歸預測輸出序列。

T=[T(t-n+1),T(t-n+2),…，T(t)]T(17)

式中:T為實際溫度向量。

兩種模型預測向量與實測向量之間的距離d為：

(18)

根據模型預測值距離實測值的偏差大小來重新分配兩個模型的權重。以兩種模型的距離來計算權重，當與實測值之間的偏差愈小占比愈大。

(19)

式中:wGM(1,1)為GM(1,1)模型所占權重，d灰為灰色二次回歸預測值與實測值之間的距離，∑d為兩種函數預測值與真值距離之和。

(20)

式中:w灰為灰色回歸權重，dGM(1,1)為GM(1,1)模型預測值跟實際溫度的距離。

在t時刻將n個軸溫監測數據更新后，模型的輸入發生變化，根據最新的輸入向量輸出預測向量，并根據(t-n)時刻的預測偏差對模型進行加權重構即：

(21)

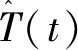
采用偏離度組合的預測模型對軸溫進行預測的步驟如圖4所示。

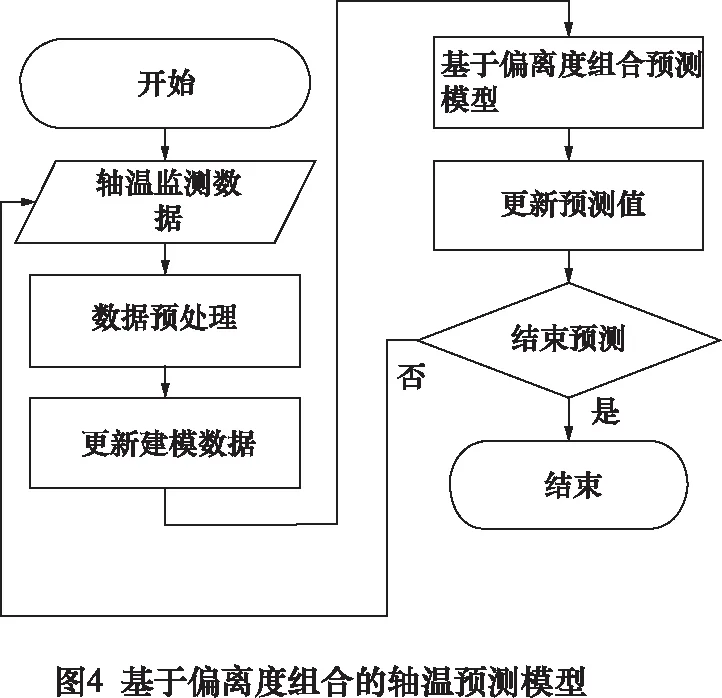
為提高模型的精度，將建模窗口內的數據及時進行更新，做到吐故納新，能夠將最新的軸溫信息運用到模型中，從而在建模數沒有變化的情況下，提高模型的預測精度，保證模型的可靠性。將模型第一次求得的預測值與之后求出的預測值拼接起來，便可得到完整的預測軸溫序列。

3.2 模型評價指標

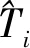
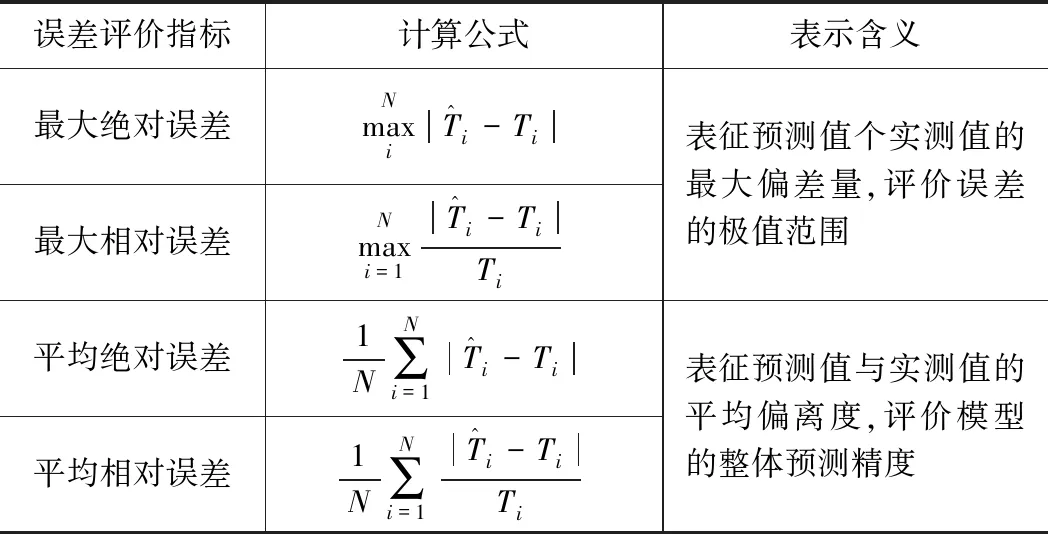
表1 預測誤差評價指標

3.3 實例驗證

以某型高速列車履歷服役軸溫監測數據為例，來驗證本文提出的模型的準確性與可靠性。以高速列車軸箱軸承溫度為例，基于軸箱軸承數天履歷數據，運用偏離度優化的預測模型對軸溫進行預測，并在每n分鐘后更新模型輸入數據，根據前一時刻單一模型預測的誤差對模型重新進行加權校正，以此優化該組合模型。圖5為高速列車溫度傳感器安裝位置示意圖。

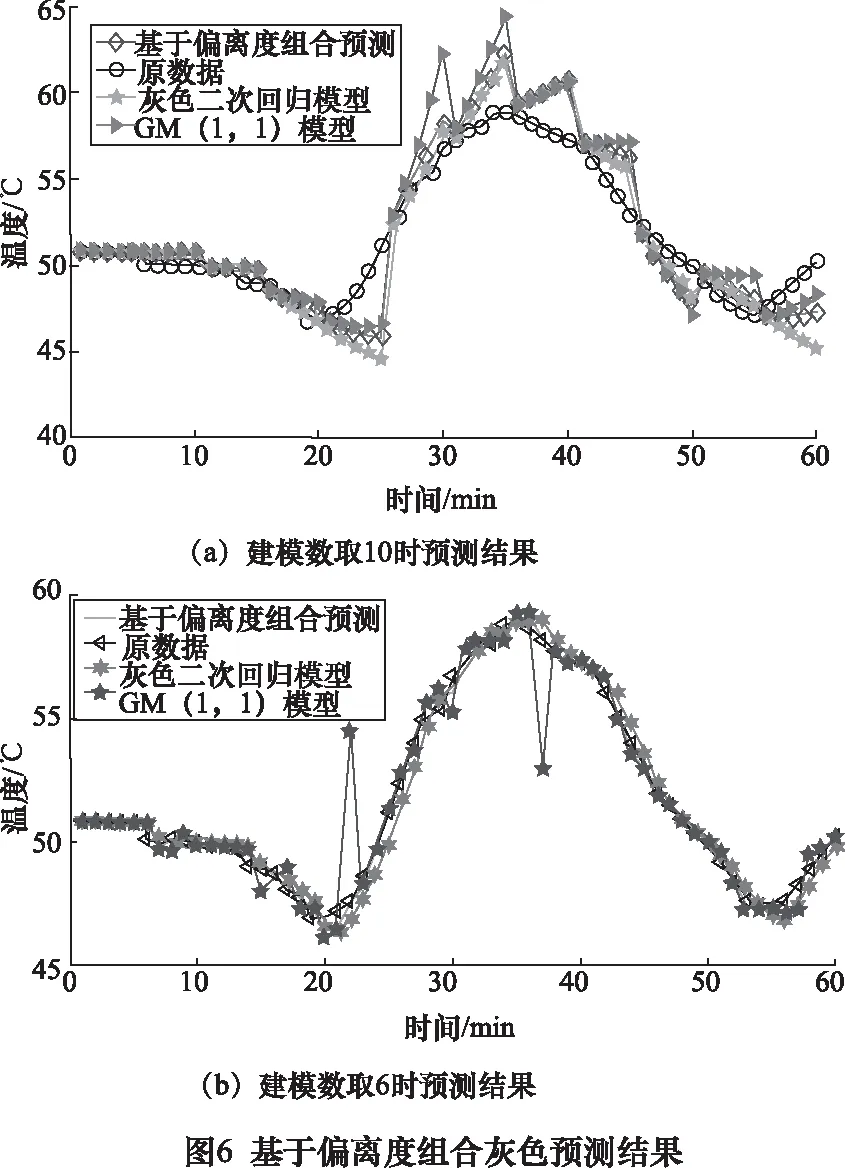
采用灰色二次回歸模型、GM(1,1)模型、基于偏離度優化的組合模型對某型高速列車的歷史軸溫進行短時預測，建模數分別取10、6時預測結果如圖6所示，預測誤差統計結果如表2所示。

對預測結果進行分析，可以看出建模數一般取6左右時有較好的擬合效果，在對軸溫進行短時預測時，基于偏離度的組合模型最大絕對誤差為0.98，平均絕對誤差為0.19。顯然，基于偏離度優化的模型較單一預測誤差明顯減少，預測精度有較大的改善，表明模型的優化作用有效。

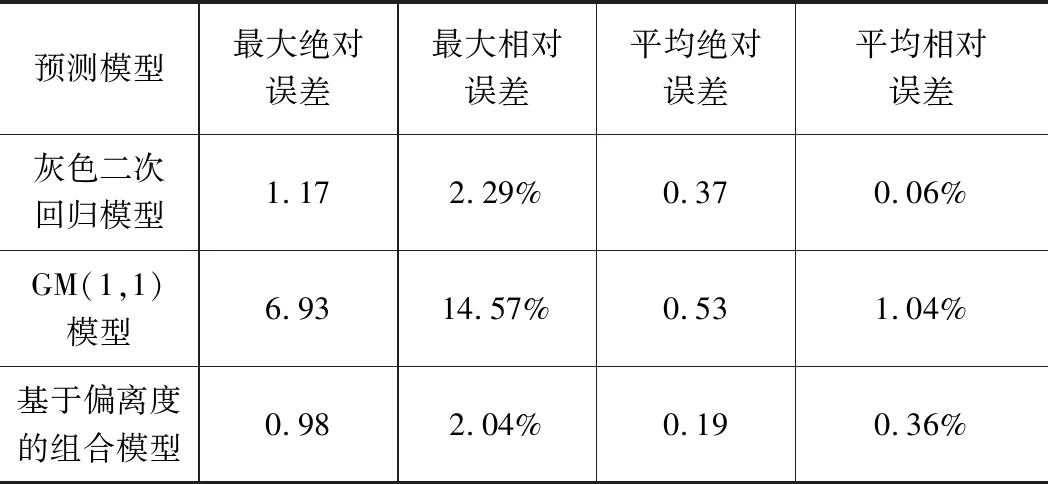
表2 基于偏離度優化的組合模型溫度預測誤差

4 結語

(1)基于GM(1,1)對單調變化的曲線擬合度較高、灰色二次回歸模型對凹凸變化的軸溫曲線擬合較好的情況，將兩個模型組合起來預測軸溫。選用某線路上實測軸溫數據對模型進行驗證，結果顯示基于偏離度優化的組合模型適應性更高，預測結果更平穩，預測精度較單一模型得到有效改善。

(2) 通過對建模數及迭代數的合理選擇，對原始軸溫數據進行預處理，保證滿足建模的需求。此外，為及時的感知軸溫變化情況，對建模窗口內的數據不斷更新，保證數據的實時性，將最新的軸溫變化情況反映出來。根據兩個單一模型上一時段預測的偏差，對單一模型的權重系數及時調整，進而重新組合預測。對異常溫升測點在未來短時間內的溫度預測，爭取到更多的處理時間，為行車策略調整提供依據。

(3)組合預測的方式可以博采眾長，整合單一模型的優點，提高模型的適用性。本文將兩個單一模型的權值系數進行偏離度優化調整，即不是均值加權的。這種方式可以避免均值加權時，組合模型不能對表現較好模型的優點充分發揮出來的情況。