軌道車輛頻變剛度轉臂節點機理研究與驗證
丁行武,卜繼玲,李曉武,楊 欣,程海濤,鄒 波
(1.株洲時代新材料科技股份有限公司, 湖南 株洲 412007;2.中車青島四方機車車輛股份有限公司, 山東 青島 266111)
隨著社會經濟的發展和人們對軌道交通的乘車體驗感要求的提高,軌道交通車輛技術得到了快速發展。為實現軌道車輛更快和更穩的目標,對軌道車輛轉向架的橡膠彈性元件提出了更高的技術要求。橡膠彈性元件在軌道車輛轉向架上應用普遍,其包括一系軸箱定位系統、二系牽引拉桿系統、電機驅動系統、齒輪箱系統和抗側滾扭桿彈性連接部位等[1]。但目前軌道車輛上應用的絕大部分橡膠彈性元件(二系空氣彈簧除外)均為單純的金屬橡膠硫化體結構形式,這種彈性元件的剛度性能不能隨車輛的振動狀態改變而變化,難以滿足軌道車輛不同運行速度和不同運行線路的要求。軌道車輛減振技術面臨著從第一代的單純橡膠減振向第二代的橡膠液體復合減振的升級換代。Hiensch等[2]指出橡膠液體復合式轉臂節點對改善軌道車輛曲線通過性能有積極作用。目前,橡膠液體復合減振技術在軌道交通領域處于探索階段,工程應用還非常有限[3-5]。事實上,橡膠液體復合式彈性元件在汽車領域早已得到了廣泛應用,尤其體現在高端乘用車領域。Barszcz等[6]、Zhang等[7]通過動力學理論和試驗方法針對汽車發動機用液壓懸置的工作特性進行了研究,分析了慣性通道參數對液壓懸置動態特性的影響規律。直接流固耦合計算方法[8-9]和集總參數模型[10-11]近年來常用作研究汽車底盤橡膠液體復合減振元件。汽車工業橡膠液體復合減振產品的應用業績引起了有關科技工作者的關注。其液壓減振的設計理念可以應用到軌道交通領域,但設計技術不可照搬,原因在于汽車底盤橡膠件主要承受高頻小振幅載荷,主要利用液壓阻尼實現減振抗沖。而軌道車輛轉向架的橡膠件主要承受低頻大振幅載荷,其重點關注的是橡膠液體復合減振元件的變剛度性能(以轉向架軸箱定位轉臂節點為例),利用變剛度來解決車輛高速運行穩定性與曲線通過性能要求矛盾問題。因此,不同于汽車底盤用復合減振彈性元件,軌道車輛用橡膠液體復合式懸掛彈性元件的流道更多設計為細長型結構。
軌道車輛軸箱定位轉臂節點連接軸箱和轉向架構架,主要傳遞縱向牽引力和制動力(沿軌道車輛行駛方向),轉臂節點的縱向剛度是其主要性能指標。縱向剛度過大將影響車輛通過曲線的能力,容易造成輪緣磨耗;縱向剛度過小則容易造成車輛出現蛇形運動失穩,影響軌道車輛的安全性能。轉臂節點這種應用特點為橡膠液體復合減振技術在軌道車輛上的應用提出了實際需求。最新研究表明,采用頻變剛度轉臂節點的軌道車輛不僅能夠保證足夠的蛇行運動穩定性,且曲線通過性能也得到明顯改善,并可降低輪緣輪軌磨耗[12-13]。
本文以某型轉向架軸箱定位轉臂節點為研究對象,開展金屬橡膠液體復合式的頻變剛度轉臂節點動態性能的機理分析與試驗研究,為后續軌道車輛金屬橡膠液體復合式懸掛彈性元件的設計、開發和應用提供參考。
1 傳統轉臂節點與頻變剛度轉臂節點對比
傳統金屬橡膠轉臂節點結構形式如圖1所示,其主要包括金屬芯軸、金屬外套和橡膠體。
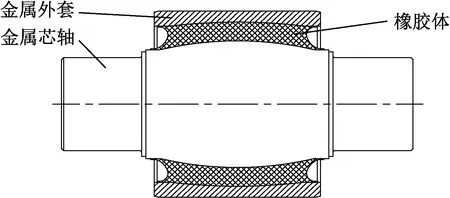
圖1 傳統金屬橡膠轉臂節點結構形式
橡膠是一種高分子黏彈性材料,硫化后形成的橡膠轉臂節點的縱向剛度在不同激振頻率下近似為一個定值。此時,轉臂節點的動態剛度Kd為
Kd=λKr
(1)
式中:Kr為橡膠體的靜態剛度;λ為橡膠體的動態倍率值,表示小振幅、高頻率的彈性系數與大振幅、低頻率的彈性系數之比,一般取值為1.0~1.6[14]。傳統金屬橡膠轉臂節點無法良好處理軌道車輛彎道通過性能與高速運行穩定性之間的矛盾,只能通過折中設計縱向定位剛度的方式來進行處理。
頻變剛度轉臂節點結構形式如圖2所示,其通過在橡膠體內嵌入設計液壓機構。液壓機構包括沿轉臂節點縱向對稱布置的兩個液壓腔和連接兩液壓腔的流道。頻變剛度轉臂節點液壓機構內部液體的流動慣性隨著激勵頻率發生實時變化,動態調節兩液壓腔之間的壓力差,進而實現低頻低剛度和高頻高剛度的頻變剛度自適應特點。
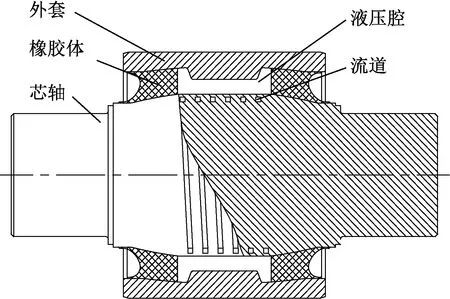
圖2 頻變剛度轉臂節點結構形式
兩種型式轉臂節點的剛度-頻率特性對比如圖3所示。
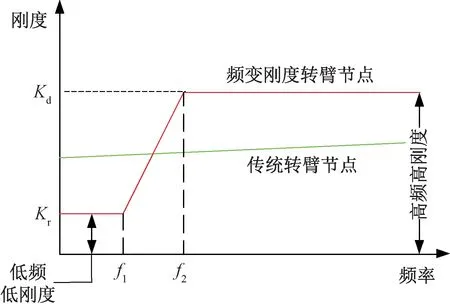
圖3 兩種型式轉臂節點剛度-頻率特性對比
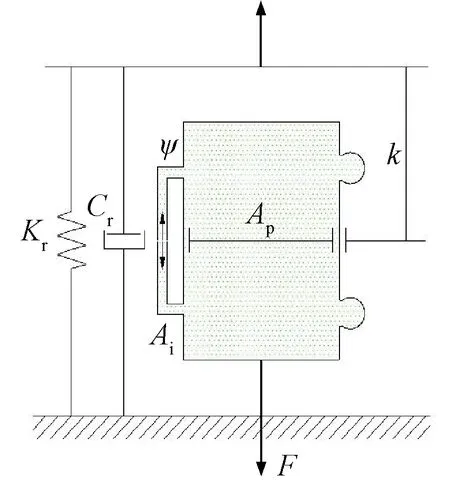
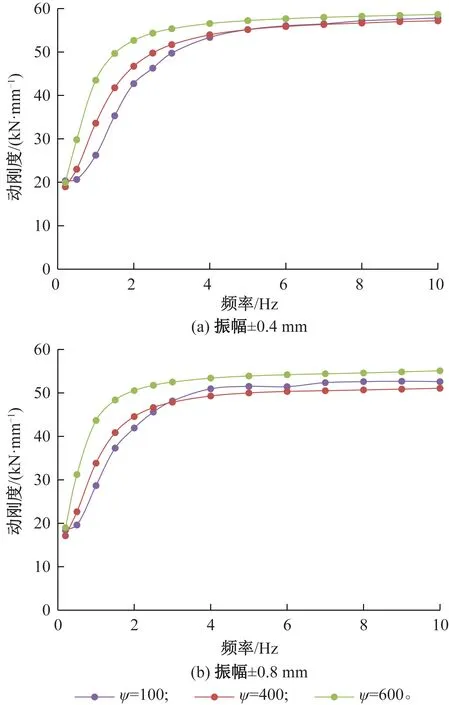
由圖3可知,頻變剛度轉臂節點剛度特性曲線存在兩個頻率特征點,即動態剛度提升頻率f1和閾值頻率f2。顯然,當f≤f1時,頻變剛度轉臂節點剛度處于準靜態剛度Kr水平;當f1 頻變剛度轉臂節點動態剛度特性存在于配置有液壓機構的縱向。金屬外套與轉向架軸箱定位轉臂上的安裝孔進行配合固定,金屬芯軸與轉向架構架相連,承受縱向力或位移激勵。簡化后的頻變剛度轉臂節點力學模型如圖4所示。 圖4 頻變剛度轉臂節點力學模型 圖4中,Kr、Cr分別為橡膠體的靜態剛度及阻尼系數;Ap為液壓腔的等效活塞面積;ψ為流道的長度l與水力直徑dH的比值,即ψ=l/dH;Ai為流道水力直徑下橫截面積,即Ai=π(dH/2)2;k為液壓腔體積柔度,表征液壓腔在流體壓力作用下的膨脹能力。假設芯軸上承受正弦位移激勵為xr(t)=Xrsin(ωt),外套的響應力為F(t),則系統剛度表示為:K=F(t)/xr(t)。 基于圖4所示的力學模型,根據流體流動質量守恒原理和液壓機構內液體的連續性方程,有 (2) 式中:Ap1、Ap2,k1、k2,P1、P2中分別為液壓機構的上、下液壓腔的等效活塞面積、體積柔度、內部液體壓力;xi為流道內流動液柱的位移函數。 頻變剛度轉臂節點液壓腔的壓力大小主要取決于液壓腔的“蓄壓”能力,即液體經過流道的壓力損失的大小。壓力損失分為局部壓力損失和沿程壓力損失。根據黏性流體沿流線的非定常伯努利方程,局部壓力損失ΔPj為 (3) 由于液體黏性的存在,流體在流道中流動時與流道壁面、流體內部不同流動層之間發生摩擦而形成摩擦阻力,形成的沿程壓力損失ΔPy為 (4) 式中:ν為流動流體的運動黏度。 存在如下關系 ΔP=P2-P1=ΔPj+ΔPy (5) 由于該頻變剛度轉臂節點兩液壓腔結構形式完全一致,即有k=k1=k2,Ap=Ap1=Ap2,將式(2)、式(3)和式(4)代入式(5),整理得到 (6) 式(6)經過傅里葉變換后整理得到 (7) 式中:Xr為激勵的位移振幅;Xi為流動液柱的位移響應振幅;φ1為xi相對于xr的滯后角度。 進一步整理,可得流道內流動液柱的位移頻響函數Hy為 (8) 位移載荷施加在芯軸上,根據力的平衡,傳遞到金屬外套上的力F(t)可表示為 (9) (10) 式(10)可表述為 (11) 進一步,可得到頻變剛度轉臂節點動態剛度Kd的計算式為 (12) 綜上可知,要想通過式(12)實現頻變剛度轉臂節點動態剛度的計算,三個關鍵參數需要通過經驗公式、有限元或者試驗的方法進行識別,即液壓腔等效活塞面積、體積柔度和局部損失系數。 頻變剛度轉臂節點液壓機構可等效為液壓活塞機構。當兩個液壓腔中的一個受到擠壓,另一側的液壓腔則會受拉伸,液體會從一個液壓腔流動到另一個液壓腔。參考如圖2所示結構,可建立求解物理模型,如圖5所示。 圖5 等效活塞面積求解物理模型 圖5中僅保留橡膠體部分,橙色區域與轉向架構架配合,紅色區域鏈接芯軸并最終與軸箱定位轉臂固結,藍色區域表示液壓腔分布位置,通過流道(黃色標識)連通縱向對稱分布的兩個液壓腔。在有限元分析軟件中,紅色區域施加固定約束,兩個液壓腔分別設置為Fluid cavity接觸,兩個液壓腔之間設置為Fluid exchange接觸。 對橡膠體內表面施加沿縱向(兩液壓腔連通方向)位移載荷xr(t),提取單個液壓腔的體積變化量ΔV,即可得到等效活塞面積Ap=ΔV/xr(t)。 在橡膠體內表面施加固定約束,對某一液壓腔內壁面施加壓力載荷ΔP,提取該液壓腔的體積變化量ΔV,即可得到體積柔度k=ΔV/ΔP。 根據軌道車輛整車動力學性能對轉向架轉臂定位節點不同的技術要求,可以設計不同結構形式的流道獲取最為理想的動態特性,比如直線型流道、連續螺旋式流道等。現針對圖4所示模型,就最為常用的如圖6所示螺旋式流道結構進行介紹。 圖6 螺旋式流道結構 螺旋式流道結構中流體從上液壓腔到下液壓腔的往復流動過程中,流道通過等截面螺旋式結構控制流體的流量大小和流動方向。螺旋式流道改變流動液柱的速度大小和方向,從而干擾流體的正常運動,內部產生撞擊、分離脫流和漩渦等現象,產生附加阻力,增加能量損失,這部分損失即為局部壓力損失。對應的局部損失系數ξ為 ξ=ξin+ξout+ξl (13) 流體由液壓腔進入流道,通流面積急劇縮小而發生的縮流壓力損失為ξout≈0.5(Ain?Aout);ξin為通流面積突然增大而產生的擴流壓力損失;ξl為彎曲損失系數,取決于流道軸心線的曲率半徑R、流道的水力直徑dH及流道的方向變化角α等參數,可通過如下經驗公式[15]計算 (14) 流體由流道進入液壓腔,通流面積突然增大而產生擴流壓力損失為[15] (15) 式中:Ain、Aout分別為流道進口、出口的橫截面積。 為兼顧直線運行穩定性和曲線通過性能,某型轉臂定位節點名義設計縱向剛度為10 kN/mm。通過運用軌道車輛系統動力學研究分析,確定解決曲線通過性能要求的轉臂定位節點剛度為5 kN/mm,直線高速運行穩定性的轉臂定位節點剛度為20 kN/mm,這樣配置轉向架的動力學性能最優,能夠解決曲線通過低頻振動的磨耗問題和直線高速運行高頻振動的穩定性問題。以此為研究對象,驗證通過上述液壓機構內嵌設計理論來實現變剛度特性及其數值模擬的準確性。該節點的使用工況條件見表1。 表1 轉臂節點性能要求 該轉臂節點液壓機構結構參數以及所用液體的物性參數見表2。 表2 頻變剛度轉臂節點結構及材料參數 頻變剛度轉臂節點試驗樣件見圖7。 圖7 頻變剛度轉臂節點試驗樣件 靜、動態剛度試驗分別在通過計量的MTS 300 kN靜態剛度試驗機和500 kN動態剛度試驗機上進行。其中,動態掃頻范圍為0~10 Hz;加載振幅為±1 mm;單頻率點循環次數為20次,記錄穩定循環5次以后的力-位移曲線和縱向動態剛度。 聯合上述公式,代入數據進行數值求解可計算得到如表2所示液壓機構的轉臂節點的縱向動態剛度為20.5 kN/mm(3 Hz)。圖8為該型轉臂節點計算結果與試驗結果對比情況,可知計算值與試驗值較接近,理論計算結果反映出來的剛度-頻率特性規律與實際情況一致。相較于傳統轉臂節點,頻變剛度轉臂節點準靜態剛度降低至傳統轉臂節點的0.5倍左右,高頻工況下動態剛度提升至傳統轉臂節點的2~2.5倍。對比式(1),圖8數據表明頻變剛度轉臂節點將傳統轉臂節點的動態倍率值從1.2左右提升至4.0~5.0。頻變剛度轉臂節點這種剛度隨振動頻率可控變化的特性為解決軌道車輛轉向架定位參數適應直線高速運行穩定性和曲線通過低磨耗的矛盾問題創造了條件。 圖8 頻變剛度轉臂節點計算與試驗剛度-頻率曲線 綜上分析可知,液壓機構是頻變剛度轉臂節點實現變剛度的根本原因,而液壓機構的兩個組成部分液壓腔和流道的結構參數則是影響這種變剛度自適應規律的核心因素。分析上述結構參數對變剛度的影響規律可為頻變剛度轉臂節點的設計及工程應用提供參考。為此將以一個系列化的流道參數來研究其規律。 設定流道長度初始值為L0,基于相同的液體和橡膠材料,在同一橫截面積A0下研究流道長度對頻變剛度轉臂節點剛度-頻率特性的影響規律,具體如圖9所示。不同流道長度頻變剛度轉臂節點的動態剛度隨著頻率的增加逐漸增加,在超過某一特定頻率點后趨于平穩。隨著流道長度的增加,在較低頻率范圍內動態剛度值不斷增加;而在較高頻率范圍內,隨著流道長度的增加動態剛度趨于相近。當流道長度增大到一定程度時,其對動態剛度的影響作用減弱。當流道長度增加到無限長時,動態剛度隨頻率變化的曲線趨于直線。圖9還說明,任意兩種不同長度的流道比較均存在一個特征頻率點f*,在該特征頻率點前后,動態剛度大小與流道長度的關系是相反的。同時,這個特征頻率點具體位置與流道長度相關,會隨著流道長度的增加而不斷前移。參考圖3可以發現,剛度提升頻率f1和動態剛度閾值頻率f2值均隨著流道長度的增加而不斷降低。 圖9 不同流道長度動態剛度隨頻率的變化曲線 設定流道橫截面積初始值為A0,基于相同的液體和橡膠材料,在同一流道長度L0下研究流道橫截面積對頻變剛度轉臂節點剛度-頻率特性的影響規律,具體如圖10所示。當流道橫截面積減小為原來的0.2倍時,流道近似“鎖止”,此時動態剛度隨頻率的變化曲線趨于直線。在較低頻率范圍內,隨著流道橫截面積的增大動態剛度值逐漸減小。在較高頻率范圍內,隨著流道橫截面積的增大動態剛度值不斷增加。隨著頻率的進一步增加,不同流道橫截面積下的動態剛度趨于相近。與流道長度影響規律類似,任意兩種不同橫截面積的流道比較均存在一個特征頻率點f*,在該特征頻率點前后,動態剛度大小與流道橫截面積的關系是相反的。同時,這個特征頻率點具體位置與流道橫截面積相關,會隨著流道橫截面積的增加而不斷后移。參考圖3可知,剛度提升頻率f1和動態剛度閾值頻率f2值均隨著流道橫截面積的增加而不斷提高。這與流道長度對動態剛度的影響規律相反。 圖10 不同流道橫截面積動態剛度隨頻率的變化曲線 液壓腔關鍵參數為等效活塞面積和體積柔度。等效活塞面積取決于液壓腔在轉臂節點軸向的分布寬度和周向分布角度。體積柔度取決于橡膠材料硬度、膠層厚度和寬度等參數。 設定液壓機構初始等效活塞面積為Ap0,研究相同流道參數和材料參數下不同液壓腔等效活塞面積對頻變剛度轉臂節點剛度-頻率特性的影響規律,具體如圖11所示。 圖11 不同等效活塞面積動態剛度隨頻率的變化曲線 由圖11可知,等效活塞面積對動態剛度的影響非常大,隨著等效活塞面積的增大,頻變剛度轉臂節點的動態剛度值均不斷增大,且這種影響會隨著等效活塞面積的持續增大而不斷加強。高頻下動態剛度穩定后,等效活塞面積每增加20%,頻變剛度轉臂節點動態剛度提升幅度逐步提高。但等效活塞面積的改變不會改變動態剛度提升頻率f1和閾值頻率f2的位置。 設定液壓機構初始體積柔度為k0,研究相同流道參數和材料參數下不同液壓腔體積柔度對頻變剛度轉臂節點剛度-頻率特性的影響規律,具體如圖12所示。顯然,液壓腔體積柔度與動態剛度強相關。隨著體積柔度的增加,頻變剛度轉臂節點的動態剛度值均不斷減小。但這種影響會隨著體積柔度的持續增加而不斷減弱。體積柔度從k0增加至1.6k0,高頻動態剛度下降32%;而當體積柔度從1.6k0增加至2.2k0,高頻動態剛度僅下降22%。可以發現,體積柔度的增加會造成動態剛度閾值頻率f2減小。 圖12 不同體積柔度動態剛度隨頻率的變化曲線 由上述分析可知,要想實現理想的動靜剛度比設計,首先要設計出合理的液壓腔,具體體現在等效活塞面積和體積柔度的設計。這兩項參數決定了頻變剛度轉臂節點高頻動態剛度整體水平,亦即最大可以實現多大的動靜剛度比;其次,通過優化流道的長度和橫截面積來調節動態剛度閾值頻率,亦即在哪個頻率點實現高頻動態剛度。 為了驗證流道長度和橫截面積對頻變剛度轉臂節點動態性能的影響,設定流道長徑比(ψ=l/dH)為因變量,并給出三種不同流道結構,分別為ψ=600、ψ=400、ψ=100,如圖13所示。 圖13 頻變剛度轉臂節點不同長徑比流道結構試驗樣件 表3為長徑比規律性驗證的試驗測試條件。圖14為兩種振幅下不同長徑比頻變剛度轉臂節點動態剛度曲線對比情況。可知,低頻范圍內長徑比越大頻變剛度轉臂節點動剛度越大,隨著測試頻率的增大不同長徑比的動態剛度比較接近。長徑比越大,頻變剛度轉臂節點動態剛度閾值頻率越小。上述規律在兩種加載振幅下表現一致,同時也反映了圖9和圖10理論計算數據所體現規律的合理性。 表3 長徑比規律性驗證測試條件 圖14 不同長徑比下頻變剛度轉臂節點剛度曲線對比 體積柔度是決定頻變剛度轉臂節點整體動剛度水平的最直接的因素。而橡膠材料屬性是決定液壓腔體積柔度的最為關鍵的因素。膠料硬度越大,液壓腔體積柔度越小。因此,此處選取了兩種膠料硬度材料來制作試驗樣件,兩種試驗樣件的體積柔度計算值如表4所示,同時測得兩種膠料樣件縱向靜態剛度分別為15.16 kN/mm(60 sha)和18.82 kN/mm(65 sha)。 表4 體積柔度規律性驗證測試條件 圖15為對應表4測試條件下的試驗結果。由圖15可知,65 sha膠料下頻變剛度轉臂節點的動態剛度大于60 sha度膠料樣件,且當動態剛度趨于穩定時不同測試頻率點兩者動態剛度的值的差趨于不變。同時,60 sha膠料樣件動態剛度閾值頻率為1.5 Hz要比65 sha膠料樣件閾值頻率2.0 Hz小。上述規律在兩個測試振幅下表現一致,表明圖12所示理論計算結果的合理性。 圖15 兩種體積柔度頻變剛度轉臂節點剛度曲線對比 (1)提出一種適用于軌道車輛轉向架軸箱定位轉臂的新型頻變剛度節點的結構設計思路,該結構通過在橡膠體內嵌設計液壓機構而成。 (2)建立該頻變剛度轉臂節點的數值計算模型,并基于該數值模型研究關鍵結構特征參數對該頻變剛度轉臂節點剛度-頻率特性的影響規律。 (3)通過制作試驗樣機和開展試驗測試,數值模型的準確性得到驗證,且規律性分析結果與測試結果也比較吻合。 (4)該新型轉臂節點表現出了理想的低頻低剛度和高頻高剛度的頻變剛度自適應特點。研究結論為橡膠液體復合減振技術在軌道車輛上的工程化應用提供了參考數據。2 頻變剛度轉臂節點力學模型建立
2.1 力學模型
2.2 模型推導
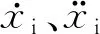
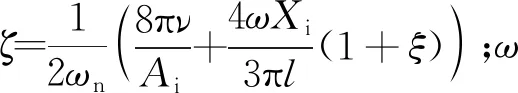
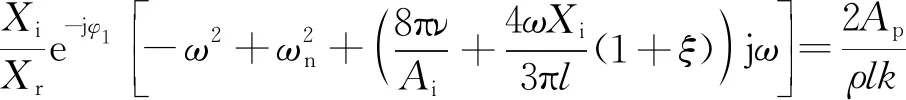
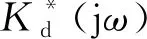
3 參數識別
3.1 等效活塞面積和體積柔度
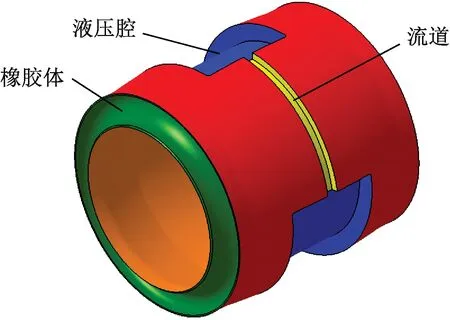
3.2 局部損失系數
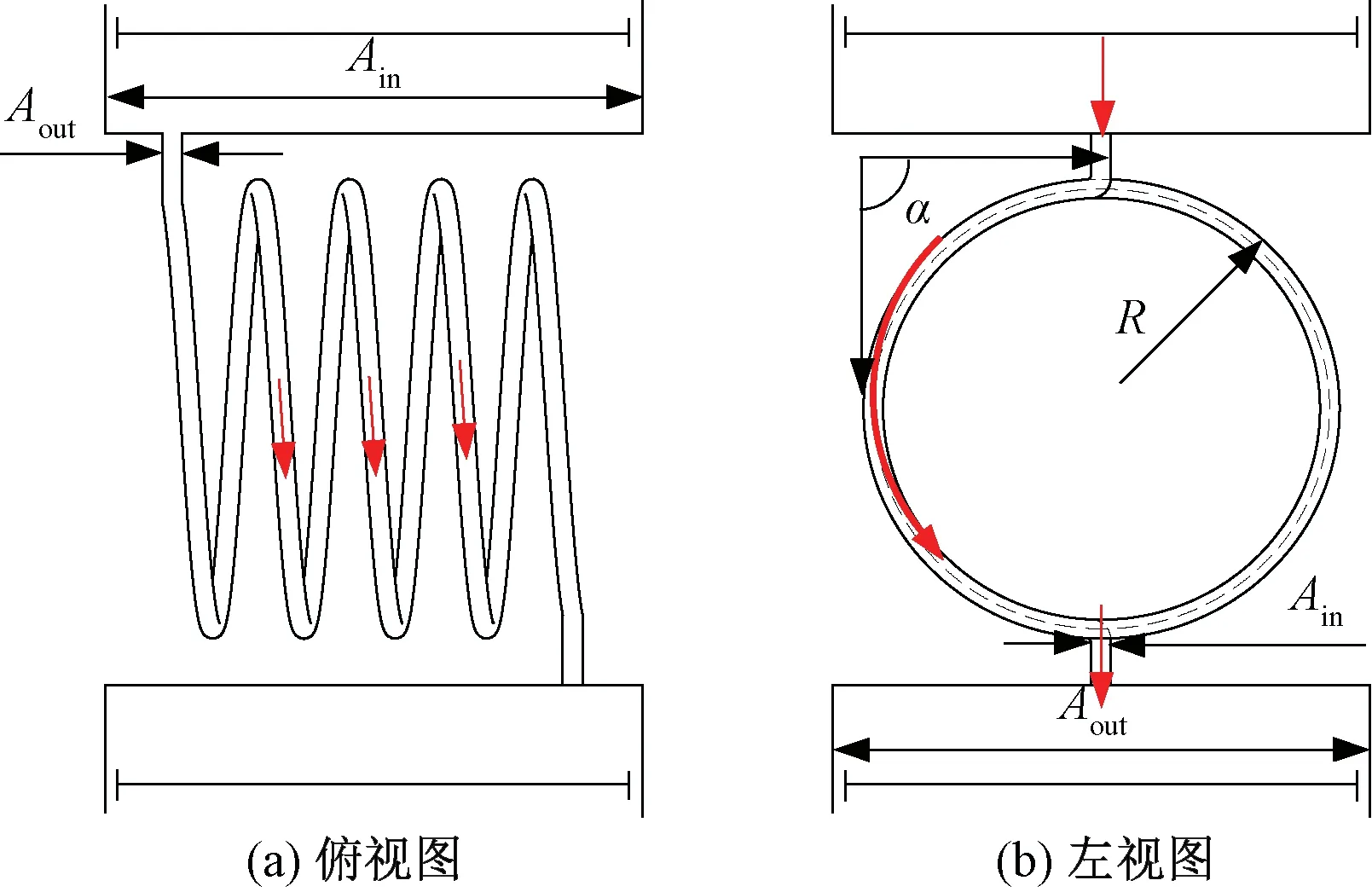
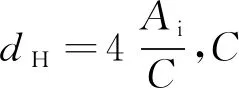
4 仿真模型驗證
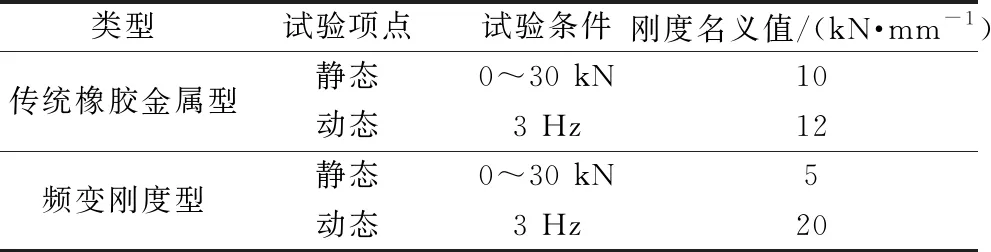

4.1 試驗條件及樣件準備

4.2 仿真結果與試驗結果對比
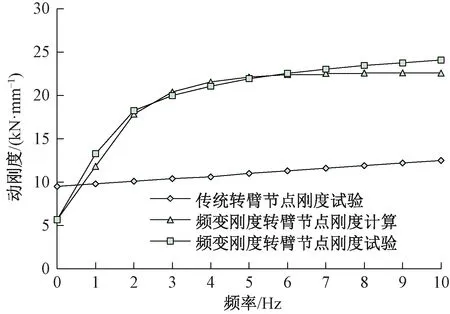
5 設計參數規律性研究與驗證
5.1 流道結構參數對動態剛度的影響
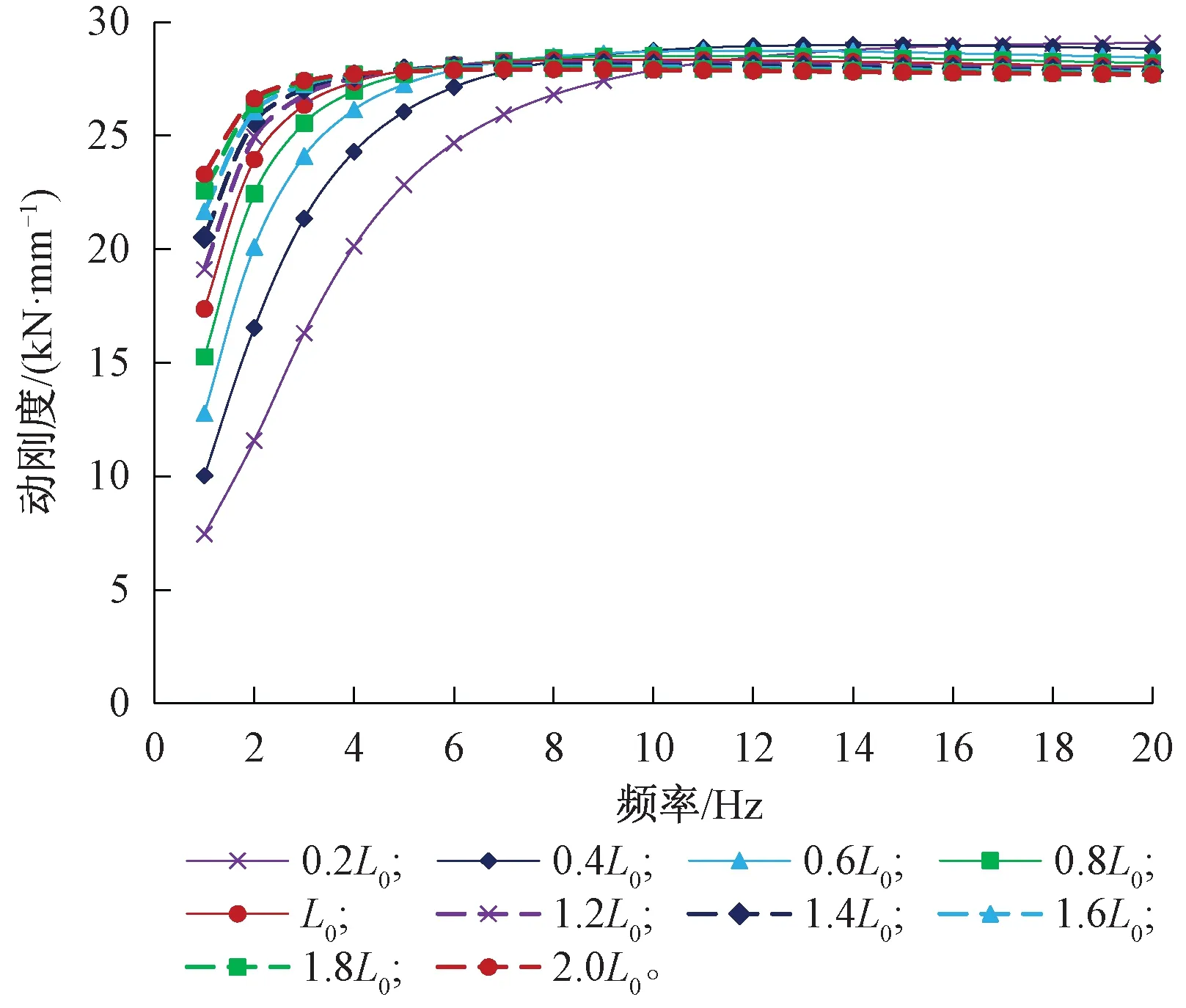

5.2 液壓腔參數對動態剛度的影響
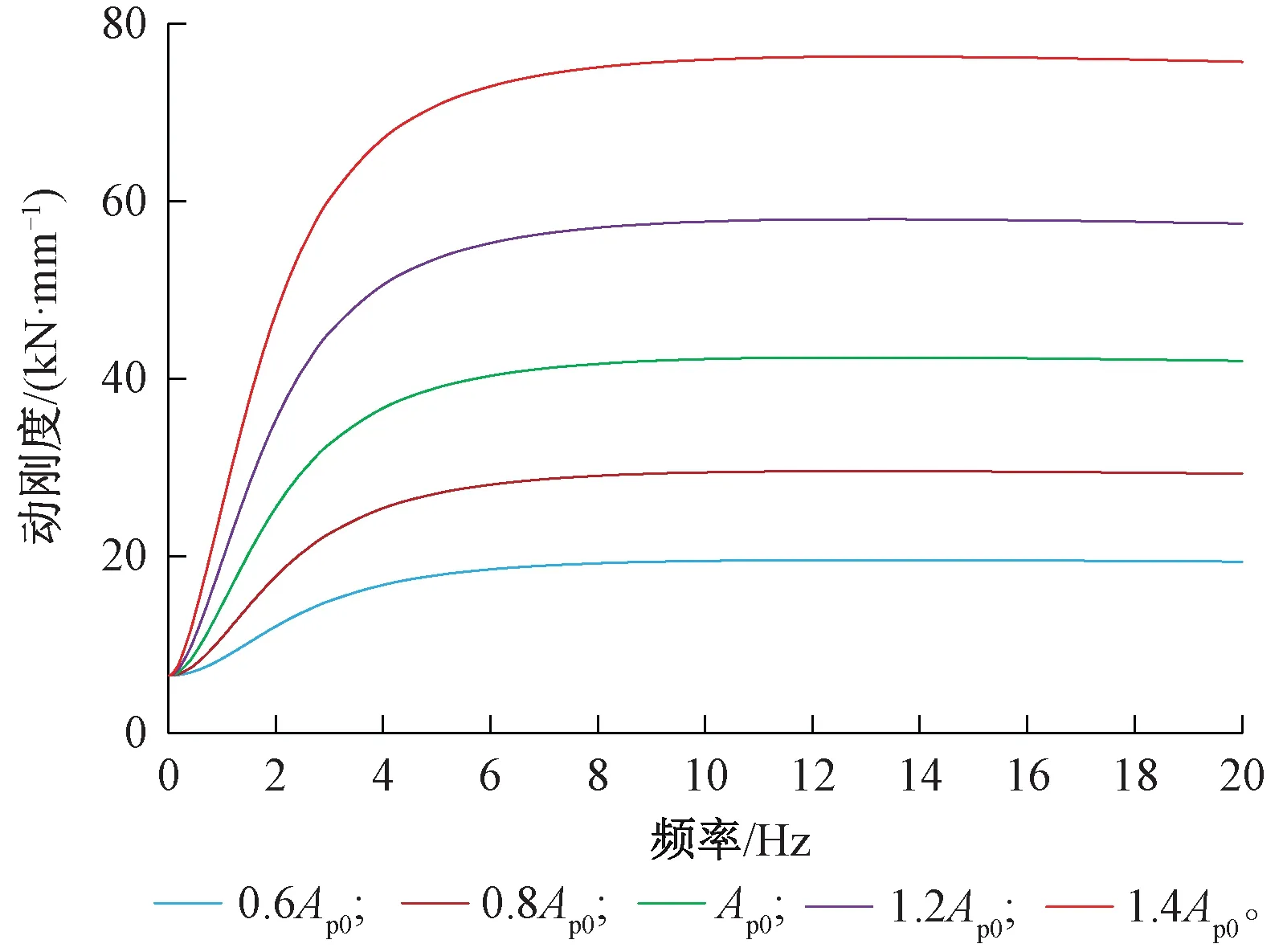
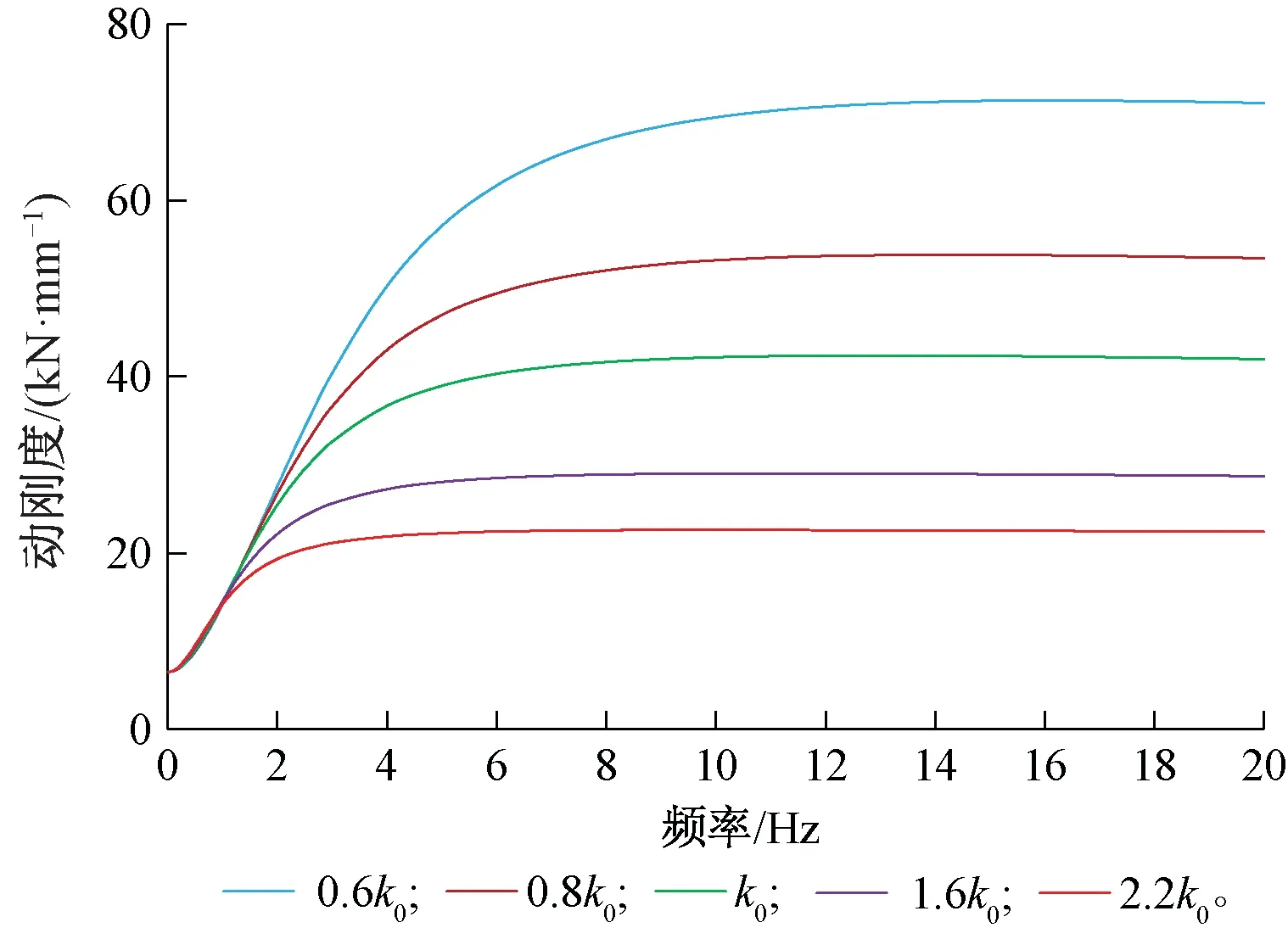
5.3 規律性驗證




6 結論

