基于翹曲切向位移模式的矩形箱梁剪力滯效應分析

張玉元，張元海，張 慧

(蘭州交通大學 土木工程學院，甘肅 蘭州 730070)

剪力滯效應是由于面內不均勻的剪切變形引起彎曲正應力沿橫向呈曲線分布的一種力學行為[1-3]。目前，國內外學者研究剪力滯效應運用最廣泛的方法是能量變分法[4-5]，其實質是通過勢能駐值原理建立箱形梁截面控制微分方程，并結合邊界條件導出相應物理量的解析解運用。文獻[6-7]選取剪力滯效應引起的附加撓度為廣義位移，將剪力滯翹曲變形從彎曲變形狀態中分離出來，作為一種獨立的變形狀態進行分析。此分析方法物理意義明確，求解過程簡單，易于工程人員理解和應用。文獻[8-9]將剪力滯效應引起的腹板平截面縱向位移納入箱梁翹曲位移中，能量變分法建立了剪力滯翹曲變形的解析理論。文獻[10]選取最大剪切轉角差為廣義位移，將初等梁和剪力滯翹曲變形狀態進行解耦分析，運用能量變分法建立了以最大剪切轉角差為未知量的控制微分方程。文獻[11]從箱梁橫截面剪力流分布規律入手，重新定義了剪力滯翹曲位移函數及修正模式。文獻[12]將剪切變形納入箱梁翹曲位移模式中，使兩種變形狀態得到了耦合求解，從而降低了求解的復雜性，提高了撓度的計算精度。

對于箱梁總勢能表達式中的剪切應變能計算，文獻中只考慮了縱向位移的偏導數，忽略了切向位移的影響，導致剪切應變能得不到正確表達。此外，諸多文獻已揭示了考慮剪力滯效應的截面縱向應力分布規律，對翹曲應力分布狀態的研究卻甚少。

本文運用廣義坐標法定義矩形箱梁的切向位移模式，選取剪力滯效應引起的附加撓度為廣義位移，運用能量變分法建立考慮切向位移影響的箱梁剪力滯效應解析理論。通過求解簡支和懸臂箱梁算例，進一步分析切向位移對箱梁剪力滯系數、附加撓度和廣義力矩的影響。

1 剪力滯翹曲位移與切向位移

如圖1所示，oxyz為直角坐標系，坐標原點o位于截面形心處，s為截面周向坐標；b1、b2分別為頂板和底板半寬，hu、hb分別為頂、底板中面至形心軸的距離，h為頂底板中面之間的距離，tu、tb分別為頂、底板的厚度，tw為腹板厚度。矩形箱梁在任意對稱豎向分布荷載q(z)作用下將發生撓曲變形，其橫截面上任一點的剪力滯翹曲位移uω(s，z)為

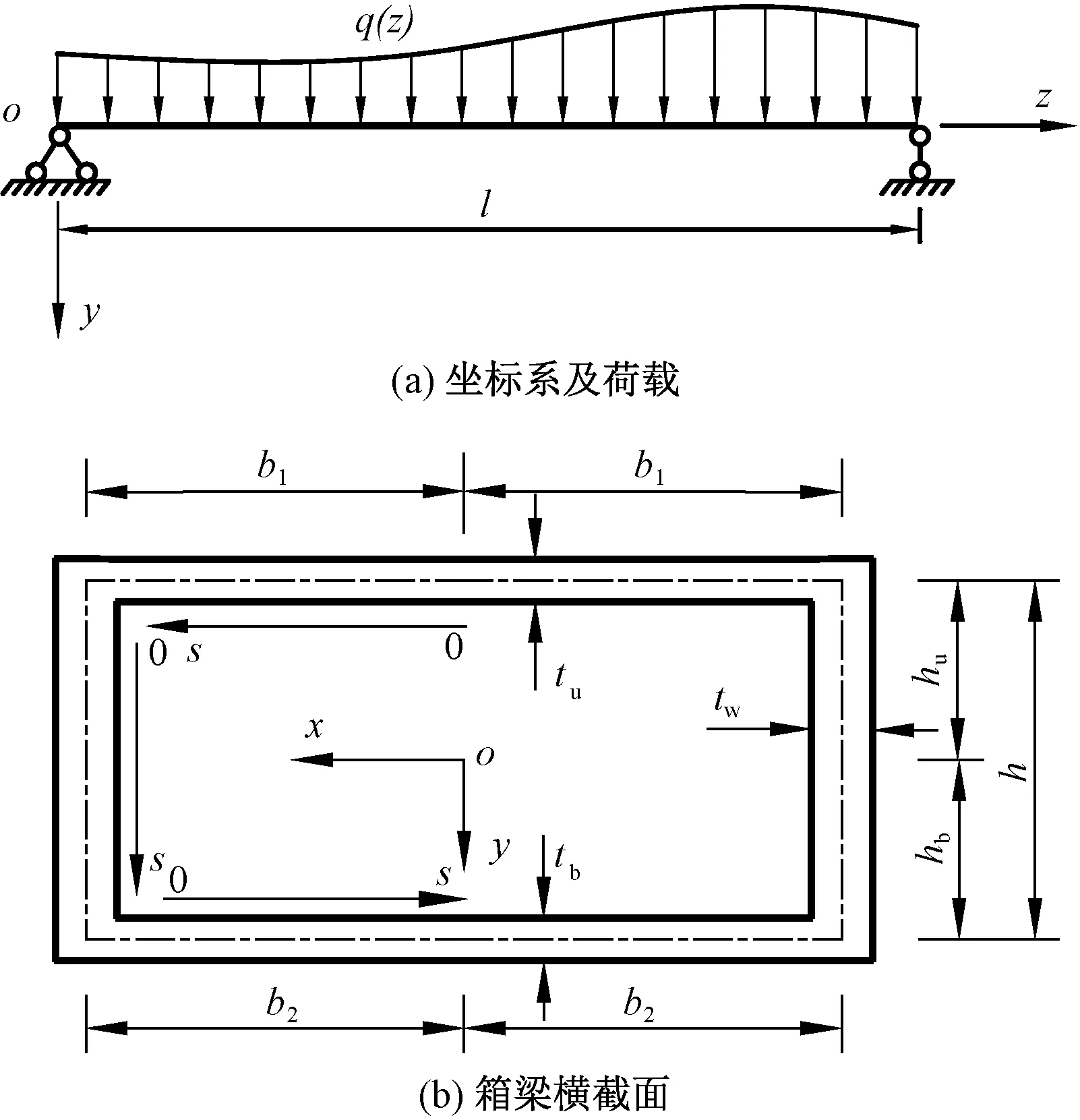
圖1 矩形箱梁簡圖

uω(s,z)=ω(s)f′(z)

(1)

式中：f為剪力滯效應引起的附加撓度；ω(s)為相應于附加撓曲轉角-f′(z)的翹曲位移函數。

選取余弦函數[8]來描述翹曲位移模式，則矩形箱梁各板的剪力滯翹曲位移函數ω(s)為

(2)

式中：η為翹曲應力自平衡修正系數；β為底板翹曲位移修正系數，即β=(b2/b1)2(hb/hu)。

根據幾何方程及胡克定律，由式(1)可得箱梁橫截面任一點的翹曲應力σω(s,z)為

(3)

(4)

式中：Ix為箱梁全截面對x軸的慣性矩；I1、I2分別為箱梁頂板和底板對x軸的慣性矩。

與剪力滯翹曲應力σω相應的廣義力矩Mω可定義為

(5)

式中：Iω為剪力滯翹曲慣性矩。

(6)

將式(3)和式(5)整理可得翹曲應力σω的另一表達式為

(7)

為了準確描述箱梁彎曲變形時切向位移沿箱室中面的分布模式，利用Ansys有限元軟件計算繪制了矩形箱梁的切向位移分布，見圖2。根據分布圖可得箱梁的翹曲變形切向位移vω(s,z)為

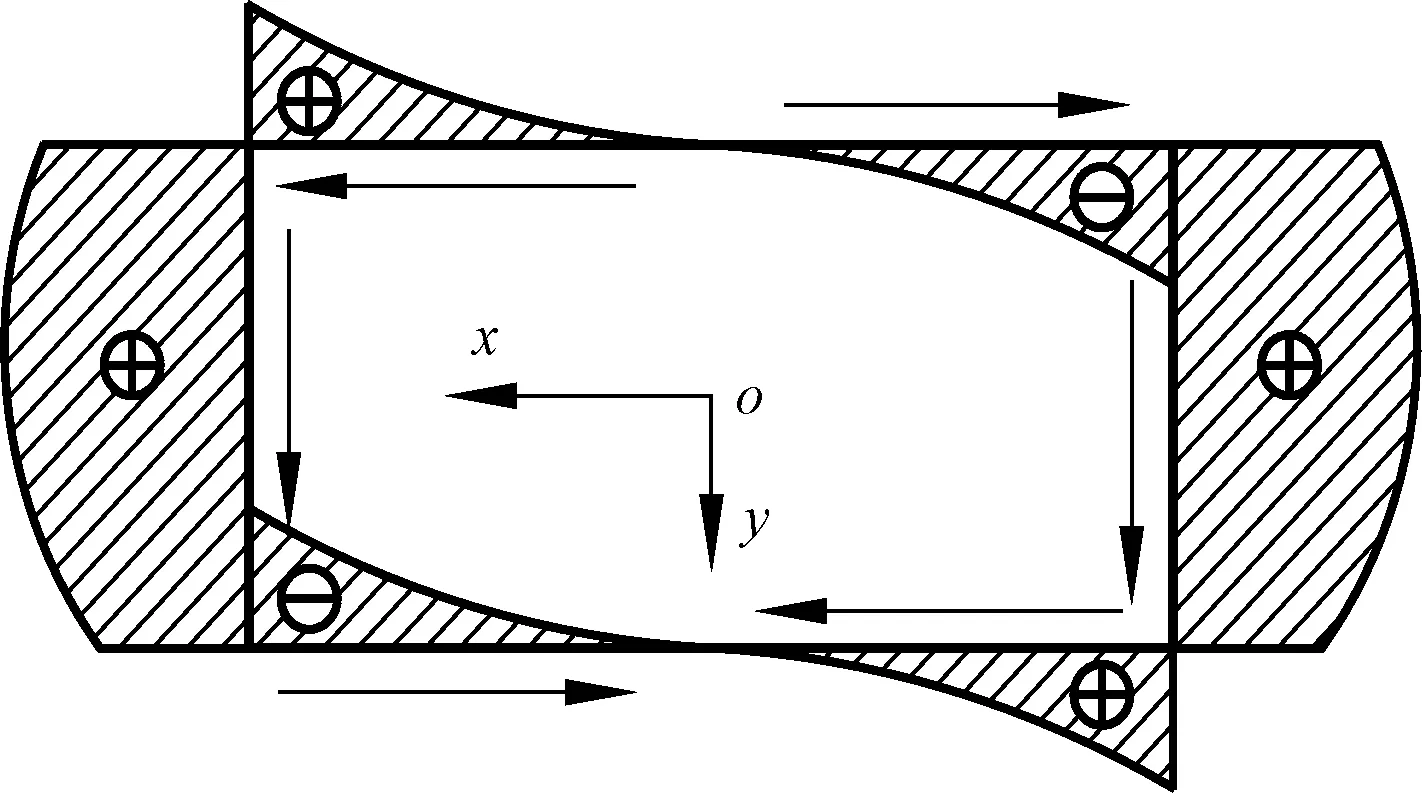
圖2 矩形箱梁切向位移分布圖

vω(s,z)=φ(s)f(z)

(8)

式中：φ(s)為切向位移分布函數。

根據圖2可得矩形箱梁左半室的切向位移分布函數φ(s)為

(9)

式中：α1、α2分別為頂板和底板的切向位移修正系數。

根據幾何方程及胡克定律，由式(1)、式(8)可得箱梁截面任一點的翹曲剪應力τω(s,z)為

(10)

箱梁發生翹曲變形時，各板在相應的二維板面內應滿足平衡微分方程。如圖3所示，在箱梁截面上任取一點P，t為微元體箱室壁厚，則位于P點處的微元體沿縱向(z軸)建立平衡微分方程為

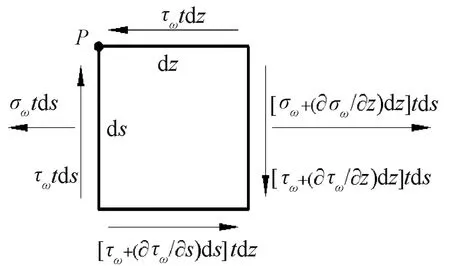
圖3 箱梁截面任一點P處的微元體

(11)

此處采用賦值法確定切向位移的修正系數，令f=f0sin(πz/l)，將其代入式(3)、式(10)、式(11)，并令s=b1，即可求得頂板切向位移修正系數α1的表達式為

(12)

式中：μ為泊松比。

同理，可求得底板切向位移修正系數α2為

(13)

2 控制微分方程及邊界條件

由彈性力學可知，箱形梁翹曲應變能為

(14)

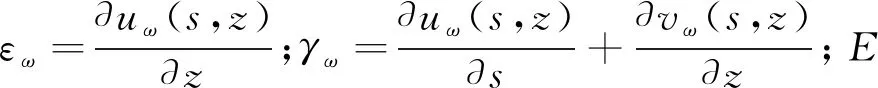
箱梁翹曲正應變εω相應的應變能U1為

(15)

箱梁翹曲剪應變γω相應的應變能U2為

(16)

式中：

(17)

外力勢能為

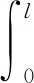
(18)

箱梁剪力滯翹曲總勢能可表達為

Π=U1+U2+V=

(19)

對總勢能泛函進行一階變分運算，并令δΠ=0，化簡可得關于附加撓度的控制微分方程為

(20)

式中：k為考慮切向位移影響的Reissner參數，即

(21)

關于附加撓度的微分方程式(20)為一個四階常系數非齊次線性微分方程，其通解的一般形式為

f=C1+C2z+C3sinh(kz)+C4cosh(kz)+f*

(22)

式中：C1、C2、C3、C4分別為待定系數，可由邊界條件求出；f*為僅與q(z)分布有關的特解。

當箱梁受均布荷載q作用時，其特解為

確定上述4個常數的邊界條件為

固定端：f=0，f′=0;

簡支端：f=0，f″=0;

自由端：f″=0，f?-k2f′=0。

3 矩形箱梁剪力滯效應解答

等截面簡支箱梁受均布荷載作用見圖4，根據式(22)結合簡支邊界條件即可求得箱梁附加撓度f(z)為

(23)

均布荷載作用時簡支箱梁截面任一點的縱向應力σ(s，z)為

(24)

式中：hi為上、下翼板中面至截面形心軸的距離；σ0為初等梁正應力。

均布荷載作用時簡支箱梁剪力滯系數λ(s，z)的計算公式為

(25)

均布荷載作用時簡支箱梁的廣義力矩Mω(z)為

Mω(z)=EIωf″(z)=

(26)

懸臂箱梁受均布荷載作用見圖5，根據式(22)結合懸臂邊界條件即可求得箱梁的附加撓度f(z)為

(27)

均布荷載作用時懸臂箱梁截面任一點的縱向應力σ(s，z)為

(28)

均布荷載作用時懸臂箱梁剪力滯系數λ(s，z)為

(29)

均布荷載作用時懸臂箱梁廣義力矩Mω(z)為

Mω(z)=EIωf″(z)=

(30)

4 算例分析

以跨度為0.8 m的矩形箱梁模型為例，截面尺寸及坐標系見圖6，坐標原點o位于截面形心處，材料彈性模量為3 GPa，泊松比為0.385，跨間作用均布荷載q=10 kN/m。

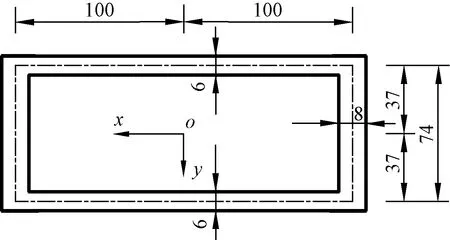
圖6 矩形箱梁截面尺寸及坐標系(單位：mm)

由于結構和荷載具有對稱性，此處只研究頂板的應力狀態即可。在考慮和不考慮切向位移兩種情況下，按照本文方法計算簡支和懸臂箱梁跨中截面計算點的剪力滯系數；利用Ansys-Solid45單元建立箱梁模型(共劃分了41 814個節點，27 600個單元)，計算得到相應點的剪力滯系數，繪制剪力滯系數橫向分布見圖7，并列出關鍵點的剪力滯系數比較見表1。

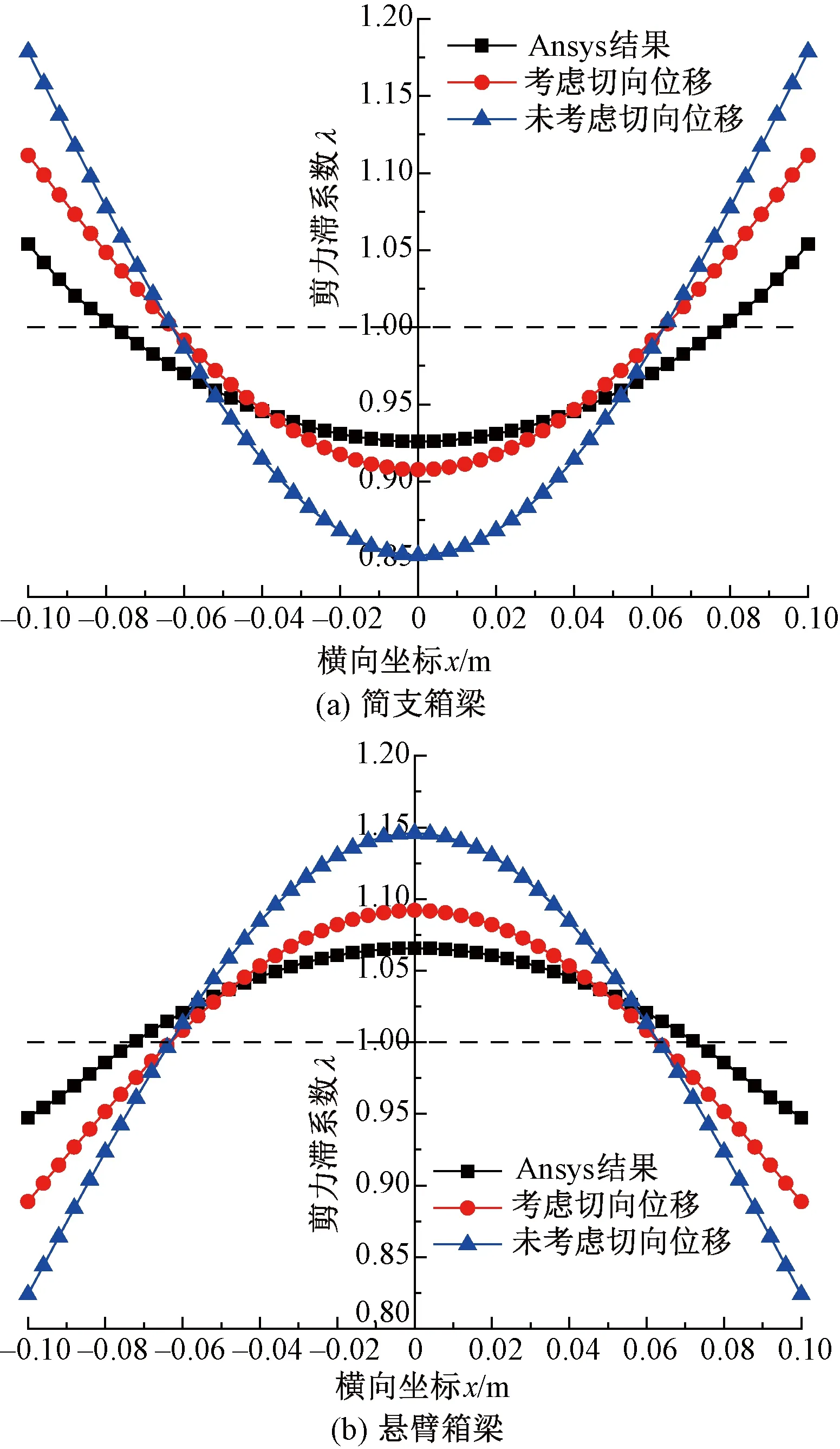
圖7 跨中截面頂板剪力滯系數橫向分布

由圖7和表1可知，考慮切向位移的計算結果與有限元數值解吻合更好，與不考慮切向位移的計算結果相比，簡支和懸臂箱梁跨中截面頂板肋處的剪力滯系數計算精度分別增加了6.03%和7.31%，頂板中點處的剪力滯系數計算精度分別提高了6.17%和4.95%。

為定量分析切向位移對矩形箱梁剪力滯效應的影響，以簡支和懸臂箱梁為例，計算并繪制頂板肋處和中點處的剪力滯系數縱向分布曲線、附加撓度及廣義力矩的縱向分布曲線，見圖8至圖10。

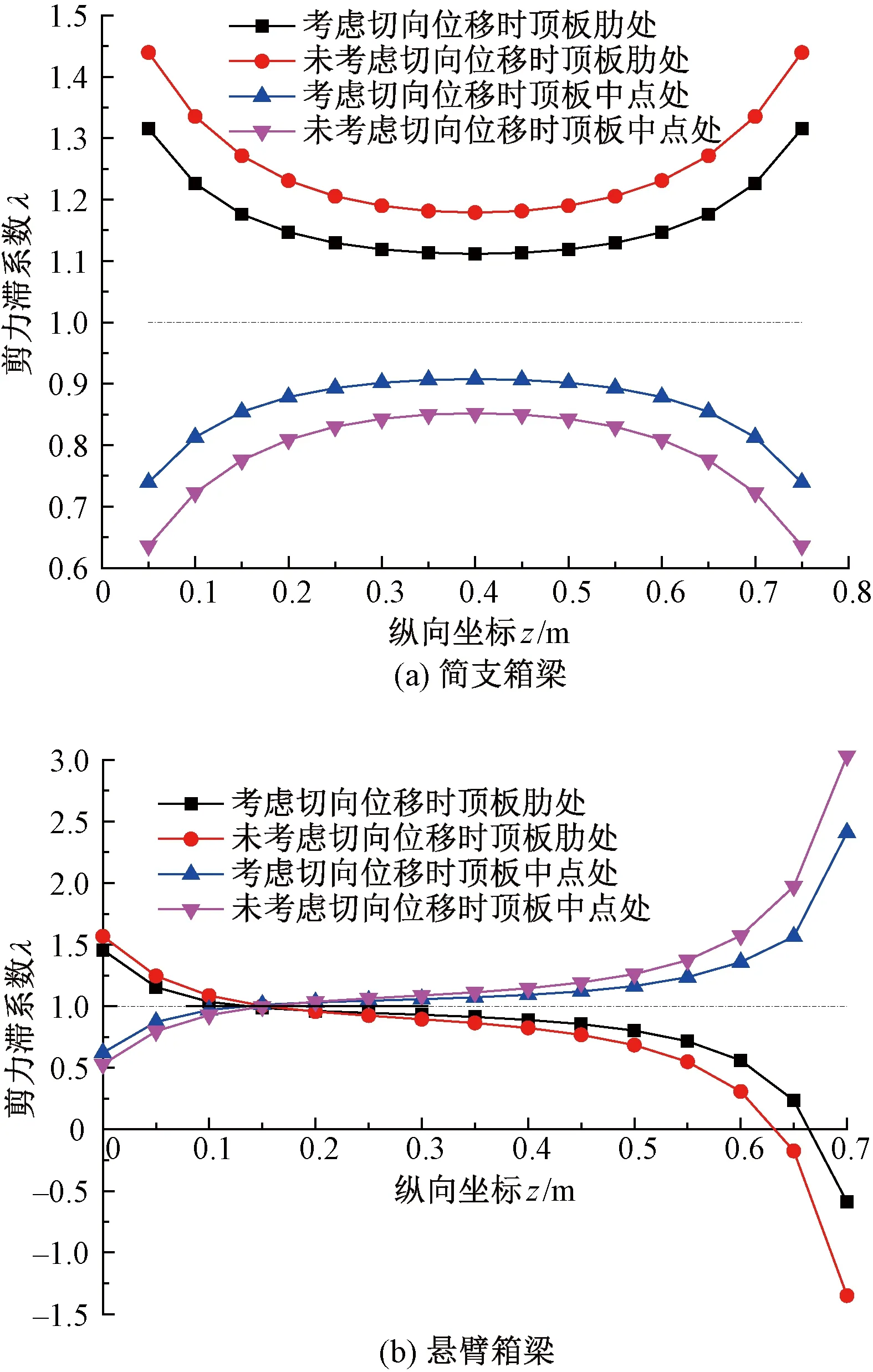
圖8 關鍵點剪力滯系數縱向分布圖

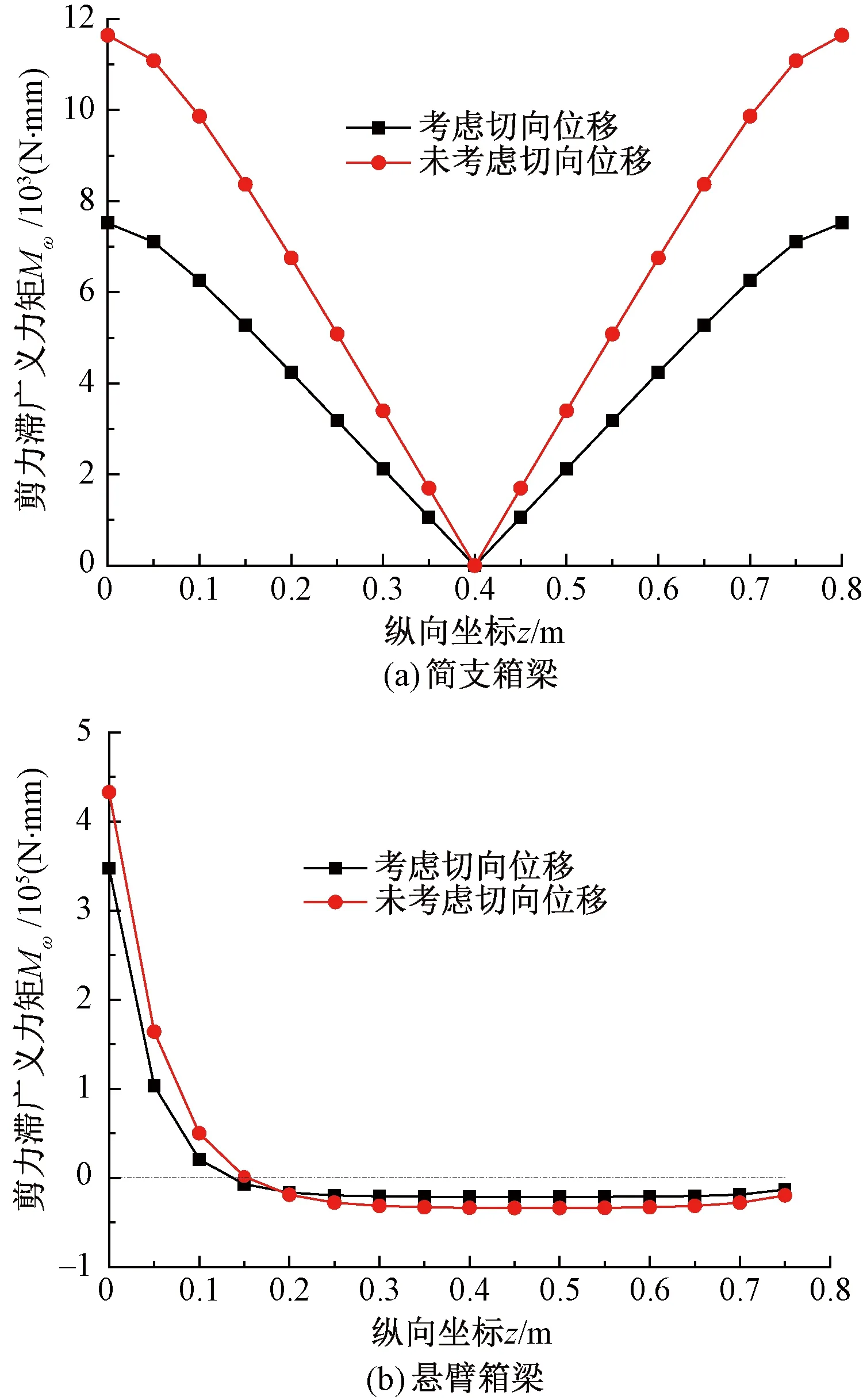
圖10 剪力滯廣義力矩縱向分布

由圖8可知，切向位移對簡支箱梁剪力滯系數縱向分布的影響顯著大于懸臂箱梁；考慮和不考慮切向位移的簡支箱梁剪力滯系數縱向分布差值比近似呈均勻分布，懸臂箱梁剪力滯系數縱向分布在梁端區域差值比較大，跨中部分差值比較小；考慮切向位移的計算結果更靠近于λ=1的水平直線，表明不考慮切向位移將會放大箱梁的剪力滯效應。

由圖9可知，考慮切向位移的剪力滯附加撓度小于未考慮的計算結果；考慮和不考慮切向位移時簡支箱梁的附加撓度差值比由支點向跨中遞增，懸臂箱梁附加撓度差值比由固定端向自由端遞增；簡支箱梁跨中截面附加撓度減小了57.78%，懸臂箱梁自由端附加撓度減小了55.49%。

由圖10可知，考慮切向位移的剪力滯廣義力矩小于未考慮的計算結果；切向位移對簡支箱梁剪力滯廣義力矩的影響遠大于懸臂箱梁；考慮和不考慮切向位移時簡支箱梁的廣義力矩差值比由支點向跨中遞減；簡支箱梁端部廣義力矩減小了54.84%，懸臂箱梁固定端廣義力矩減小了24.59%。

5 結論

(1)采用廣義坐標法定義了矩形箱梁各板的切向位移模式及其分布函數，選取剪力滯效應引起的附加撓度為廣義位移，運用能量變分法建立了考慮切向位移影響的箱梁剪力滯效應解析理論。算例分析表明，考慮切向位移的計算結果與有限元數值解吻合更好，從而驗證了本文方法的正確性。

(2)剪力滯系數分析表明，考慮切向位移時簡支和懸臂箱梁跨中截面頂板肋處的剪力滯系數計算精度分別提高了6.03%和7.31%，剪力滯系數縱向分布曲線更靠近于λ=1的水平直線。

(3)考慮切向位移的剪力滯附加撓度和廣義力矩均小于未考慮的計算結果。簡支箱梁跨中截面和懸臂箱梁自由端處的附加撓度減小了57.78%和55.49%；簡支箱梁端部和懸臂箱梁固定端處的廣義力矩減小了54.84%和24.59%。