考慮SSI的自復位框架抗震性能研究

張 真 李培振

（1.同濟大學結構防災減災工程系，上海200092；2.同濟大學土木工程防災國家重點實驗室，上海200092）

0 引 言

一般在進行結構設計時，通常運用“剛性地基假定”，不考慮場地土與結構的相互作用，這種假定在地基剛度比結構剛度大很多的情況下是適用的。但對于上部結構剛度較大而地基土的剛度較小這一情況，如結構位于軟土地基上且土層覆蓋較厚、場地較軟弱時，這種假定所帶來的誤差往往是比較大的。而對于自復位搖擺結構而言，雖然其本身由于放松了柱腳與基礎以及柱與梁之間的連接，剛度相對傳統結構而言有所降低，但在軟土地基上時，土體與結構兩者間的剛度可能還會比較接近，這時再按剛性地基假定對其進行設計可能是不合適的。

以往學者在進行各類搖擺框架及自復位結構抗震性能評估時，大都集中在結構本身的研究，對搖擺自復位結構的支承條件，即地基土對搖擺自復位結構的約束對結構性能的影響考慮較少。地基土-結構相互作用是影響結構地震響應的重要因素，這種動態相互作用包括地基對結構體系動態特性的影響以及結構對地震動輸入的影響。通常的研究方法是截取一定區域的地基土并在其邊界處設置人工邊界。常用的人工邊界有黏性人工邊界、黏彈性人工邊界和無限元人工邊界等。對于三維黏彈性人工邊界的研究，劉晶波等［1］基于球面波動理論提出的三維黏彈性人工邊界，在節點處并聯彈簧和阻尼器，這種方法克服了黏性邊界低頻失穩的缺點，能模擬遠域地基的彈性恢復力，具有廣泛的適用性。

在人工邊界上實現波動輸入時，不同的人工邊界所采用的方法不同，對于黏彈性人工邊界，劉晶波等通過研究，將地震波轉化為等效節點荷載輸入，能讓人工邊界上的輸入位移與原自由場的相同，取得了不錯的計算效果。本文采用黏彈性人工邊界及地震動等效荷載理論，運用MATLAB編制的程序實現等效節點荷載及黏彈性人工邊界條件的輸入［2］。利用ABAQUS軟件建立位于軟土地基上的自復位框架結構考慮土-結構相互作用的數值模型，分析了考慮土-結構相互作用后結構動力特性的影響。對土-結構相互作用體系進行了動力時程分析，得到了自復位搖擺結構的動力響應，并與剛性地基假定下的結構響應進行了分析對比。

1 自復位框架簡介

根據Lu等［3］提出的受控搖擺框架的概念，魯亮等［4-5］提出了“體外預應力自復位框架”（External Prestressing Self-centering Frame，EPSCF）和“受控搖擺鋼筋混凝土框架”（Controlled Rocking Reinforced Concrete Frame，CR-RCF）的新型結構抗震體系，并建立了EPSCF、CR-RCF的相應力學模型和數值分析模型。本文在此基礎上重新設計了兩種體外預應力自復位框架：C40混凝土自復位框架、Q345鋼結構自復位框架。除梁和柱所用材料規格不同外，兩種自復位框架結構其余參數完全相同，自復位框架布置圖如圖1所示。為了分析對比阻尼器及支撐對自復位框架的控制作用，將阻尼器和支撐去掉，建立了兩個模型的中間狀態——無控搖擺框架，以便比較。

圖1 自復位框架示意圖（單位：mm）Fig.1 Schematic diagram of the self-centering frame（Unit：mm）

所有自復位框架結構的樓板厚度取為120 mm，所有鋼筋強度等級取為HRB335，樓面恒載取為4.0 kN/m2，活載取為2.0 kN/m2，混凝土強度為C40，混凝土密度取2 500 kg/m3，鋼材選用Q345，鋼材密度取7 800 kg/m3。自復位框架結構的設計按照常規框架，參照《混凝土結構設計規范》和《鋼結構設計規范》進行，使用PKPM進行驗算，鋼框架和混凝土框架的設計均符合建筑設計規范的要求。對于混凝土自復位框架結構，梁截面尺寸取200 mm×300 mm，配筋225，325，柱截面取為300 mm×300 mm，配825的鋼筋；對于鋼結構自復位框架，柱截面尺寸取400 mm×400 mm×50 mm的箱形截面，梁選用300 mm×400 mm×20 mm×15 mm的工字形截面梁。自復位框架結構的基礎形式采用柱下獨立基礎，尺寸為1 m×1 m×0.5 m，基礎混凝土采用C30，泊松比取為0.2，參考文獻［4］中的力學推導公式，按照基于位移的設計方法，以罕遇地震作用下結構的層間位移角限值5%為設計目標，得到相關設計參數如表1所示。

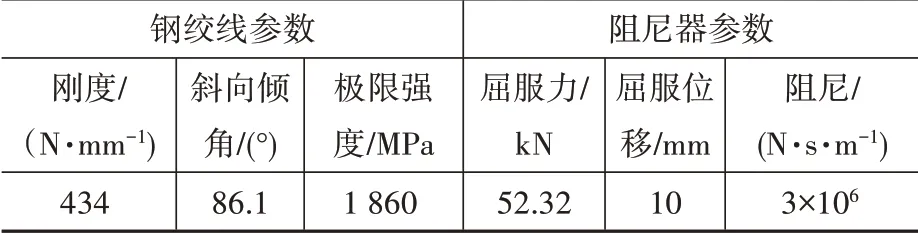
表1 相關設計參數Table 1 Parameters of design

2 地震動輸入原理

2.1 地震作用下的人工邊界

根據劉晶波等［6-7］的研究分析，三維黏彈性人工邊界可以等效為在邊界節點上分布的一系列三向并聯的彈簧-阻尼器系統，如圖2所示。

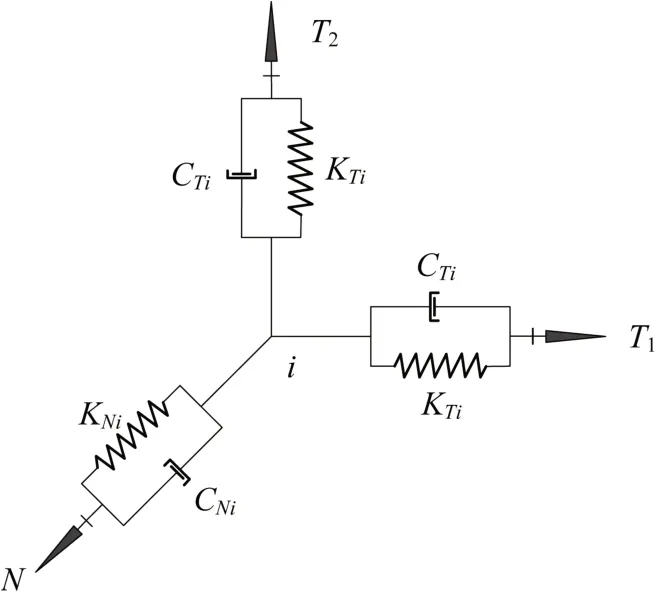
圖2 三維黏彈性邊界示意圖［6-7］Fig.2 Diagram of 3D viscoelastic boundary［6-7］

其中，彈簧剛度系數和阻尼器的阻尼系數為

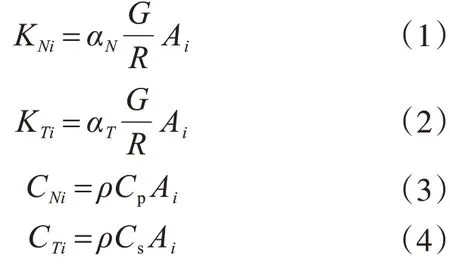
式中：ρ、G分別為地基土的密度和剪切模量；R為散射波源到人工邊界的距離；αN、αT為參數［8］，取αN=1.33、αT=0.67；A i為節點邊界節點i的影響面積；Cp、Cs分別為地基土的壓縮波波速和剪切波波速，設地基土的泊松比為υ，則其計算公式為

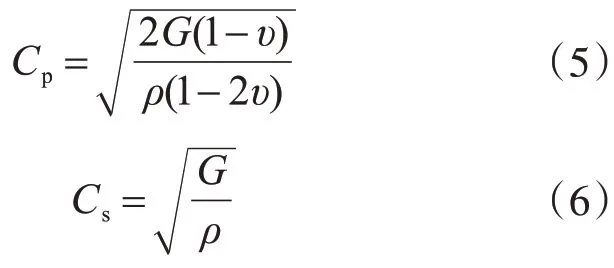
2.2 黏彈性邊界地震動輸入

地震動輸入采用應力（等效節點力）輸入的方式。應力輸入是引入無限地基介質的本構關系，將單側波動滿足的偏微分方程轉換為施加在人工邊界的應力，假設人工邊界節點i處的自由波場位移向量、速度向量和加速度向量分別為{u i}、，根據體系的動力平衡方程：

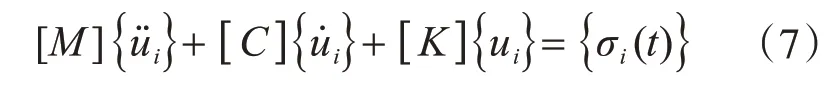
式中：[M]、[C]、[K]分別為質量、阻尼、剛度矩陣；{σi(t)}為施加在邊界節點i處的等效節點應力。

對求得的節點應力，再乘以相應的節點影響面積A i得到節點力F i(t)。以壓縮波從底邊入射為例，則等效節點力［2］按下式計算：

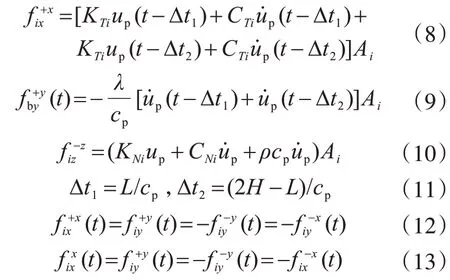
式中：H為底邊界到地表的距離；L為節點i到底邊界的距離；up和u?p分別為入射壓縮波的位移和速度時程；f(t)的上角標表示邊界點外法線方向，下角標表示等效節點力的方向。

根據上述計算公式，基于MATLAB軟件程序實現黏彈性邊界條件以及等效節點荷載的計算，以關鍵字*Amplitude，*Cload，*Springs，*Dashpot輸出荷載和彈簧阻尼器的inp文件，通過在ABAQUS原inp文件中添加關鍵字*include實現對邊界條件的施加以及荷載的輸入。已經通過算例驗證此種方法是可行有效的［2］。

3 考慮土-結構相互作用的自復位框架結構數值模型

3.1 數值模型基本參數

本文采用ABAQUS建立兩種體外預應力自復位框架模型，依照第1節中相關設計參數建模。框架梁柱均采用梁單元建模，通過*rebar命令在混凝土梁柱中插入鋼筋，整個模型中梁柱鉸接采用MPC鉸連接，鋼絞線的性能采用預拉軸向單元模擬，阻尼器則采用滑槽單元模擬。參考文獻［9］，樓板采用殼單元，通過分成殼的方法在樓板中插入鋼筋。通過在樓板上施加非結構質量的方法考慮恒載與活載對結構的影響。考慮到常規框架結構可能在大中震條件下進入塑性，混凝土自復位框架梁柱材料采用PQ-fiber材料模型，鋼結構自復位框架梁柱材料采用的是屈服強化模型，屈服時應變取0.01。基礎和土體采用實體單元建模，基礎與土體間的法向接觸采用“硬接觸”，切向接觸采用摩爾庫倫摩擦模型，摩擦系數取0.3。地基土采用摩爾庫倫本構模型，選取軟土作為分析對象，密度為2 000 kg/m3，彈性模量取3.6×107Pa，泊松比取為0.3，內摩擦角取為10°，黏聚力取24 kPa。土體的長寬均取為結構長寬的5倍［10］，高度取為50 m，整個土體取75 m×50 m×50 m，并且地基土的網格劃分滿足單元尺寸與地震波波動頻率間的計算精度要求［11］，整個體系的三維仿真模型如圖3所示。

圖3 數值仿真模型Fig.3 Numerical simulation model

3.2 動力特性分析

采用Block Lanczos法分別對土-結構相互作用（Soil-Structure Interaction，SSI）結構體系和剛性地基（Rigid Foundation，RF）假定下的結構體系進行了模態分析。在求解土-結構相互作用結構體系自振頻率時，采用了無質量土體模型，忽略了土體的質量而只考慮其剛度對結構動力特性的影響。工程上一般考慮結構的前三階頻率，現在將前三階頻率列于表2。

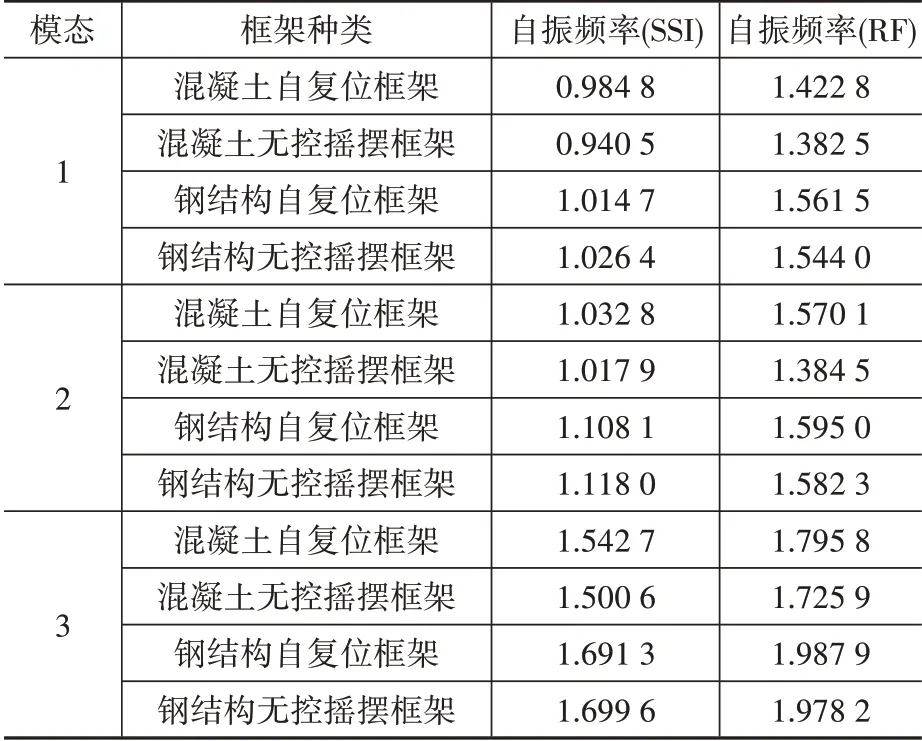
表2 混凝土框架在兩種情況下自振頻率對比Table 2 Comparison of natural frequencies between two cases

由表2可以看出，去掉阻尼器及支撐后，混凝土自復位框架前三階自振頻率都有所降低，說明去掉阻尼器及支撐使得混凝土自復位搖擺結構變柔。對于鋼框架搖擺自復位結構，在同樣去掉阻尼器和支撐的情況下，剛性地基條件和考慮SSI結果的變化趨勢不一致。總體而言，考慮SSI以后，自復位框架結構的自振頻率有較大降低（在30%左右），說明對于自復位框架結構而言，考慮SSI會較大程度增加整個結構體系的柔度，使自振周期變長，自振頻率降低明顯。

4 考慮土-結構相互作用的自復位框架結構地震響應分析

本文利用反應譜生成程序Spectrum_Chinese和反應譜轉人工波生成程序SIMQKE-GR分別考慮8度抗震設防烈度下二類場地，第二組在頻遇地震（0.07g）、設防地震（0.20g）、罕遇地震（0.40g）三種工況下的地震波［12］，圖4給出了罕遇地震下的時程曲線。假定地震波位于土體底部，方向為x向（圖中土體長邊方向），沿土體向上傳播。進行剛性地基上的結構響應分析時，將地震波在自由場表面產生的加速度時程作為激勵輸入，計算得到結構樓層的位移響應、加速度響應和柱剪力響應。

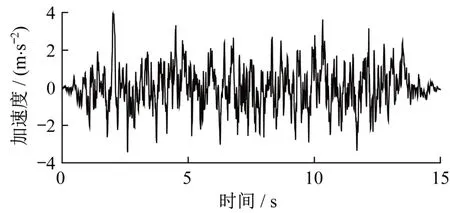
圖4 罕遇地震加速度波時程曲線Fig.4 Acceleration time history cure of rare ground motion

結構的阻尼采用Rayleigh阻尼，即阻尼矩陣為質量和剛度矩陣的組合［13］，按式（14）、式（15）進行計算，其中的系數α和β可由結構的一階圓頻率ω1、二階圓頻率ω2以及相關的阻尼比ξ得到，參照文獻［14］和文獻［15］，對于混凝土結構取ξ=0.05，鋼結構取ξ=0.04。

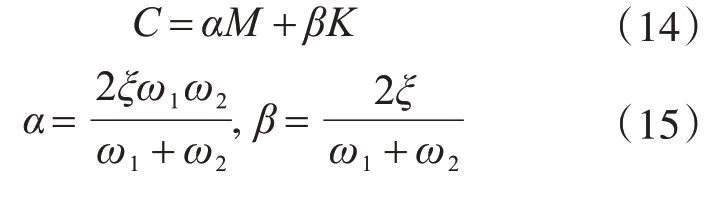
4.1 自復位框架位移響應

自復位框架在不同工況下的樓層相對位移響應最大值如表3所示，根據表3中層相對位移響應計算得到考慮SSI后不同自復位框架的位移增幅，如表4所示。從表4以及圖5可以看出，相比于剛性地基假定，考慮SSI后，自復位搖擺結構的位移增幅是要大于無控搖擺結構的，這說明考慮SSI后，自復位搖擺結構的位移控制效果變差。

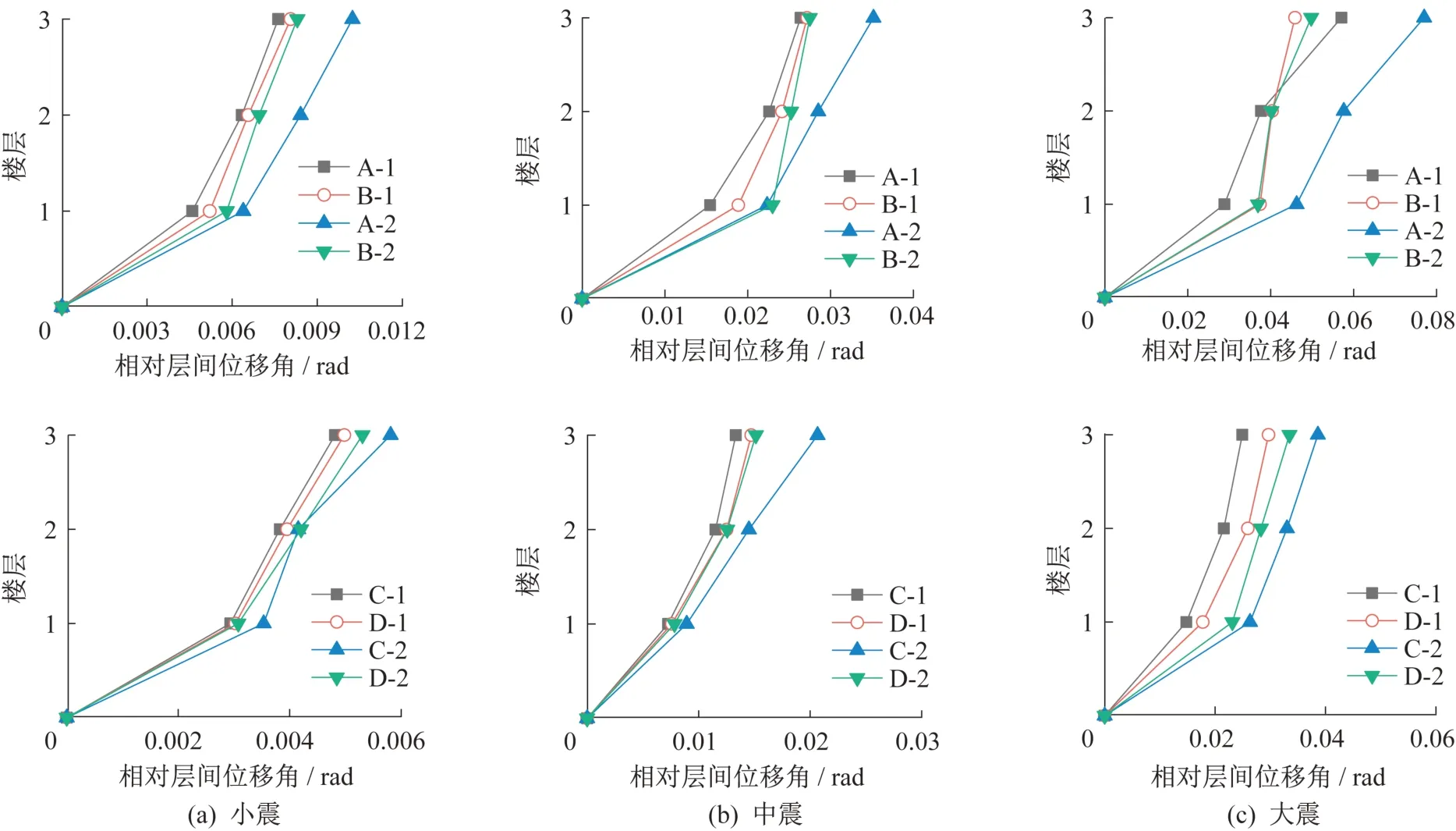
圖5 不同自復位框架相對層間位移角響應最大值Fig.5 Maximum inter-story displacement angle response of different self-centering frames

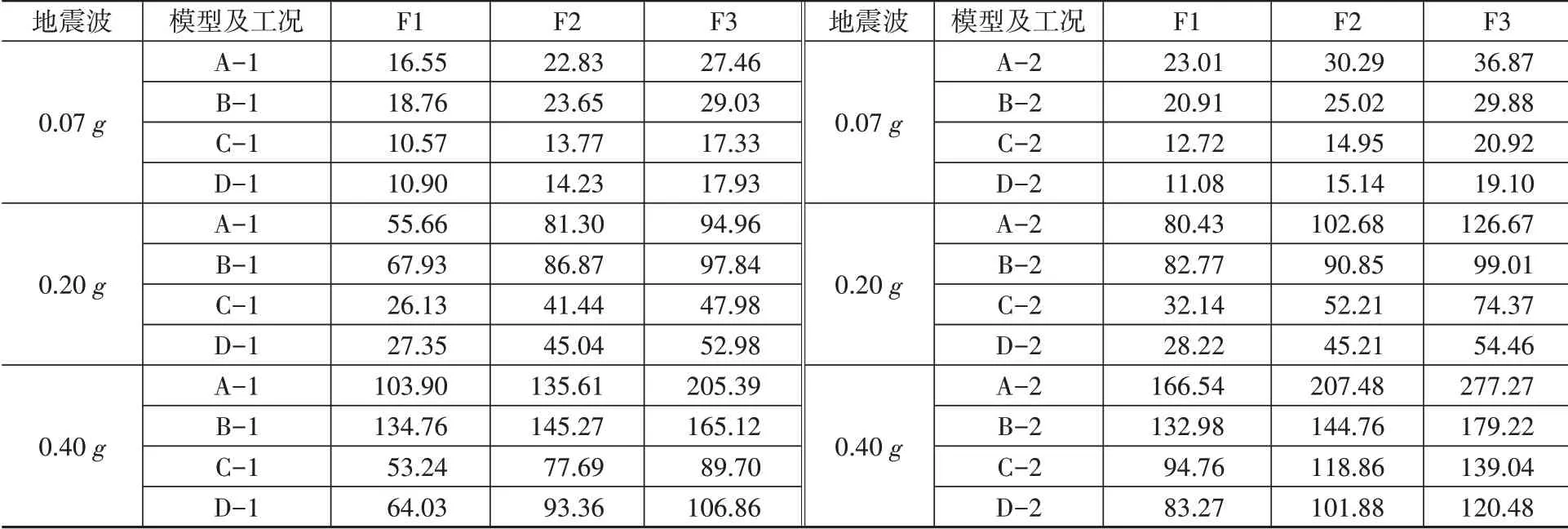
表3 自復位框架結構層相對位移響應Table 3 The relative story drifts response of the self-centering frame mm

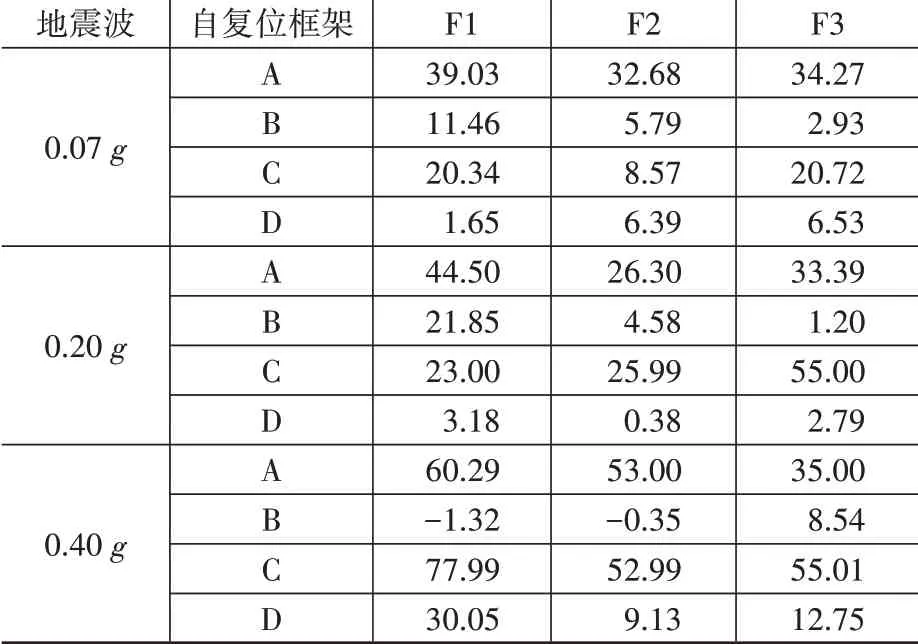
表4 考慮土-結構相互作用后不同自復位框架的位移增幅Table 4 The displacement increment of different selfcentering frames after considering soil-structure interaction %

從表3數據可以看出，在剛性地基條件下，阻尼器的施加能有效控制自復位結構在中震和大震條件下的位移，使其比未設置阻尼器的自復位結構的位移要小，但在考慮了SSI以后，中震和大震下結構的相對層間位移顯著增大。考慮SSI以后，在大震作用下，混凝土無控搖擺框架的層間位移角已經超過了第1節中預設的5%，說明軟土地基上設計此類結構需要考慮SSI，才能得到合理結果。

4.2 自復位框架加速度響應

兩種材料類型的自復位搖擺結構在剛性地基假定條件以及考慮SSI下的三種地震作用水準下的樓層加速度響應最大值如表5所示。在剛性地基條件下自復位框架的樓層加速度隨樓層的變化趨勢與考慮SSI下的情況樓層并不一致，如果按剛性地基假定進行分析，可能錯誤分析最不利樓層的位置。

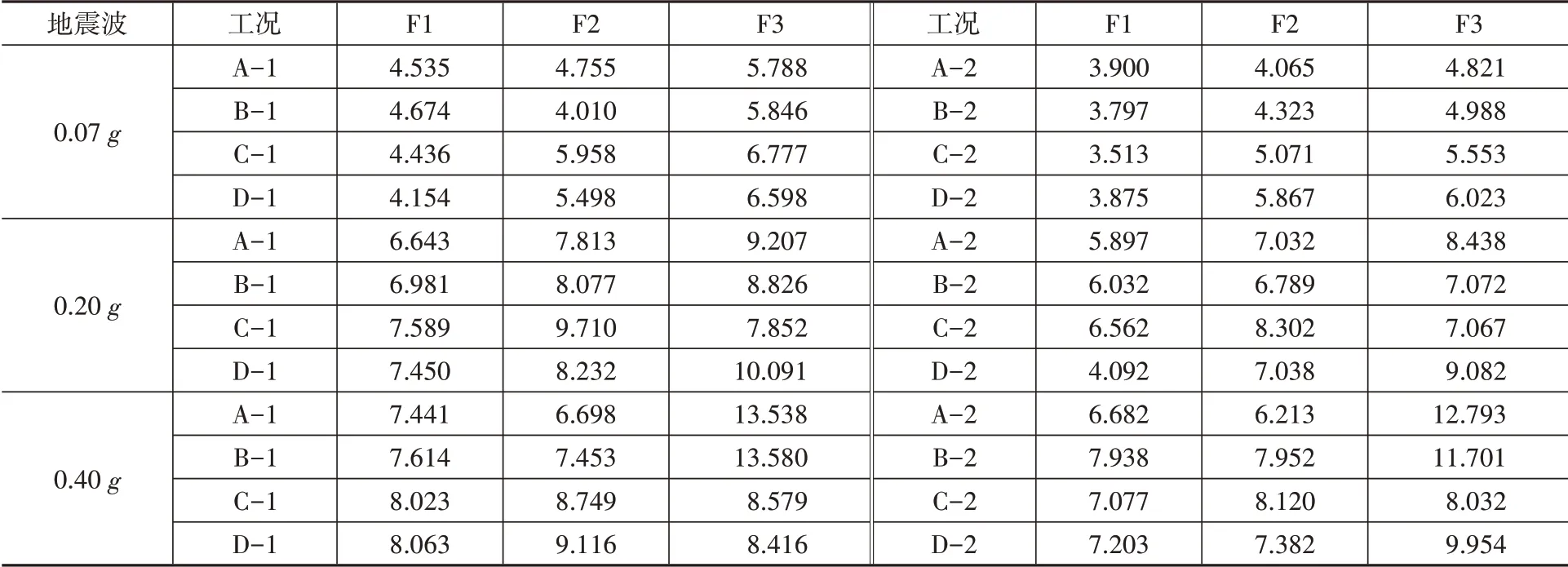
表5 自復位框架加速度響應Table 5 The acceleration response of self-centering frame m/s2

為了便于比較，定義加速度峰值放大倍數K：

式中，ag，max、as，max分別表示剛性地基、考慮SSI條件下的樓層加速度響應最大絕對值。

三種地震水準下的加速度響應放大倍數如圖6所示。可以看出，兩種不同材料類型的自復位框架在剛性地基條件下對樓層加速度具有一定的放大作用，這是由于剛性地基條件下，結構頻率偏長、周期偏短所致。

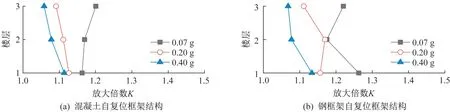
圖6 自復位框架結構剛性地基假定較考慮SSI情況下的加速度放大倍數Fig.6 The magnification of self-centering frame structure under earthquake

4.3 自復位框架內力分析

兩種不同材料類型的自復位搖擺結構在剛性地基假定條件以及考慮SSI的三種地震作用水準下的各樓層中間柱的峰值剪力絕對值如表6所示。從表6可以看出，考慮了SSI后，兩種自復位框架結構的剪力都有所增大，根據文獻［16］所述，這是由于在土體底部施加了黏彈性柔性邊界后放大了結構對剪力的響應。但相比于剛性地基假定條件，考慮SSI時阻尼器對自復位框架結構的剪力變化影響并不一致，有控自復位結構和無控自復位結構在考慮SSI后的剪力可能比較接近甚至出現前者大于后者的情況，這說明按傳統剛性地基假定來設計自復位框架結構可能不安全。

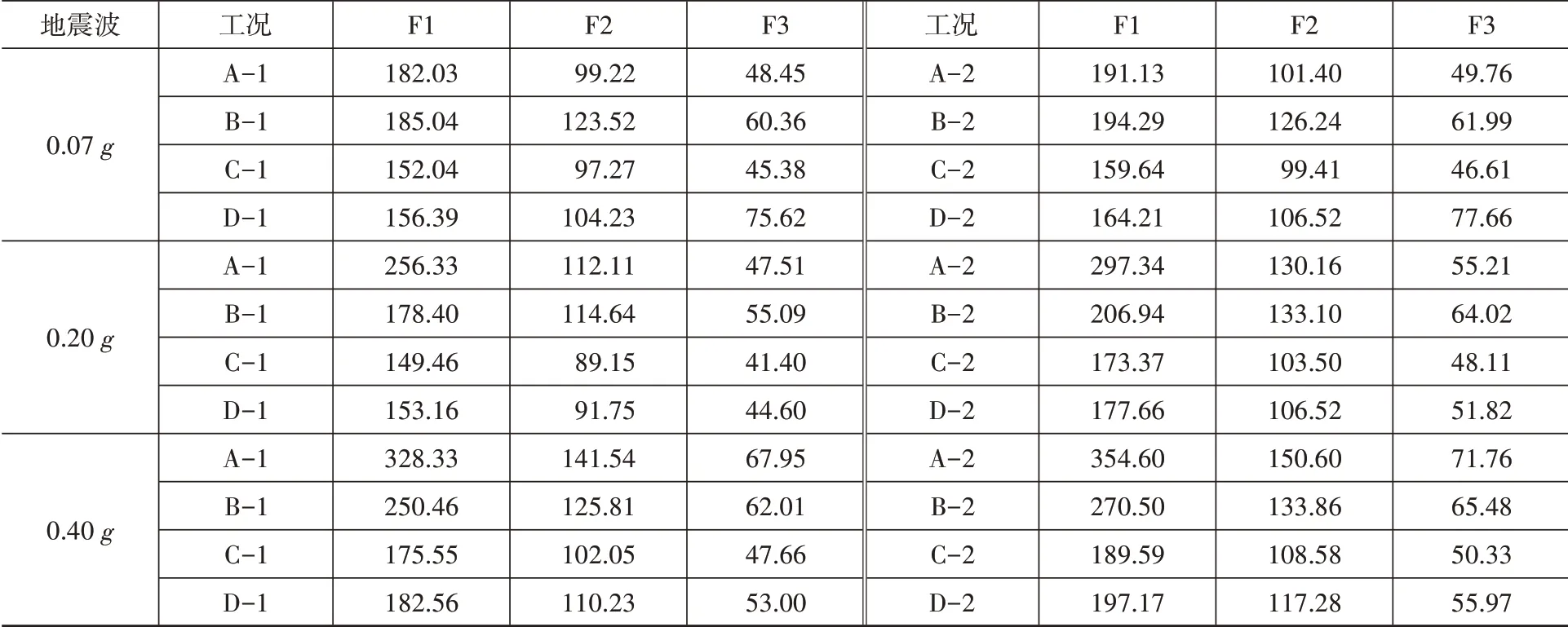
表6 自復位搖擺結構中間柱剪力響應Table 6 The story-level shear forces of middle column of self-centering frames kN

5 結 論

本文根據有關學者提出的體外預應力搖擺框架新型抗震體系，做了適當改進，重新設計了兩種材料類型的自復位框架，結合土體黏彈性邊界條件的相關理論，運用ABAQUS以及MATLAB軟件編寫有關程序實現邊界條件的輸入以及有限元模型的建立，通過等效荷載模擬輸入8度地震波，分析了自復位搖擺結構在剛性地基條件以及軟土地基工況下考慮SSI后的抗震性能，得出以下結論：

（1）考慮SSI后，自復位搖擺結構的自振頻率都有較大降低；對于鋼框架自復位結構，阻尼器及支撐對結構自振頻率變化的影響在剛性地基及軟土地基兩種情況下存在差異。

（2）考慮SSI后，結構的層間位移都有較大增加，具有耗能阻尼的自復位框架的可控性達不到預期效果，僅僅依據剛性地基假定時的位移限值來設計自復位框架結構，可能達不到設計預期。

（3）考慮SSI后，自復位框架結構的樓層加速度響應雖有所減少，但柱的剪力有所增加。柱剪力的增大將使得自復位框架結構不能承受更大的地震作用，所以在軟土地基上進行自復位框架設計時應考慮SSI效應。