論體外預應力筋加固混凝土梁正截面承載能力計算的合理性

單成林 鄭小紅

（華南理工大學土木與交通學院，廣州510640）

0 引 言

目前，對體外預應力筋加固混凝土梁正截面承載力計算時，國內規范［1-4］、相關著作［5-7］，國內外論文［8-13］都將體外預應力筋作為有黏結受拉鋼筋考慮，即作為構件承載力的一部分，參與到截面承載力組合中。這種做法似乎已墨守成規，形成了固定思維。由于預應力加固混凝土結構有很好的使用效益，體外預應力筋加固結構的工程越來越多，本文從三方面來論證這一做法帶來的疑問及不合理性。

1 如何考慮體外預應力筋的作用

舉個簡單的示例，用體外預應力筋加固矩形截面鋼筋混凝土簡支梁，在靠近截面受拉邊（下方）的兩側用一對體外預應力鋼筋對梁端施加一對壓力，如圖1所示。

圖1 用兩根體外鋼筋對簡支梁施加預壓力Fig.1 Applying prestress to the simply supported beam with two external steel bars

在做跨中正截面承載力計算時為簡單起見，不考慮受壓鋼筋A′s作用，正截面計算圖示如圖2所示，按傳統方法計算抗彎承載力時，對受壓區合力點取矩及水平力平衡：

圖2 矩形截面鋼筋混凝土受彎構件正截面承載力計算圖示Fig.2 Graphical calculation of normal section bearing capacity of reinforced concrete flexural members with rectangular section

式中：Mu為抗彎承載力；fsd，As，hs分別為原受拉鋼筋的抗拉強度設計值、截面面積及重心至受壓邊緣距離；x為受壓區高度；fcd為混凝土抗壓強度設計值；σpu，Ap，hp分別為體外筋的極限應力、截面面積及重心至截面受壓邊緣距離；b，h分別為矩形截面的梁寬和梁高。

顯然承載力計算式（1）中含有體外預應力筋項。現在將體外預應力筋移除，對該梁采用圖3的方式用千斤頂對梁端施加一對壓力，即在梁端相同位置施加一對相同的壓力。毋庸置疑，用體外筋加力和用千斤頂直接頂住梁端原體外筋位置加力的受力圖示都是圖4，對梁的受力來說，兩者作用效果完全相同，但后者沒有體外筋，此時如何計算其正截面抗彎承載力？顯然傳統的計算方法無法解釋這一現象，而將梁端錨固點的等效節點力作為外力，將對計算截面產生的卸載彎矩參與到作用效應組合中，而不是作為截面承載能力來計算就很清楚，受力也明確。實際上，體外預應力筋對梁的作用采用接觸點的等效節點力計算也是過去計算截面應力時常用的方法。還有現今在承載能力計算時將體外筋當成有黏結筋對待，但在正常使用極限狀態應力計算時，換算截面的幾何性質計算中又不計入體外筋，而采用原截面的換算截面幾何性質，本身就有矛盾。

圖3 在簡支梁的兩端用千斤頂施加預壓力Fig.3 Preloading with a jack at both ends of the simply supported beam

圖4 簡支梁兩端施加預壓力受力圖Fig.4 Diagram of prestressing force applied to both ends of simply supported beam

2 平截面假定問題

現今，對混凝土梁的設計都首先假定鋼筋與混凝土黏結可靠，正截面計算的平截面假定按定義是構件受力后沿正截面高度范圍內混凝土與有黏結縱向受力鋼筋的平均應變呈線性分布，對混凝土梁來說，在開裂截面處，由于受拉鋼筋的相對滑移不完全符合平截面假定，但對整個構件來說，裂縫只是局部的、很少量的，總體來說基本符合平截面假定。現今的理論計算和規范都是基于此假定計算梁的正截面承載力及應力。但體外筋作為無黏結受拉鋼筋，與混凝土梁體無黏結，整根索長范圍相對每個截面都存在滑移，這就不是局部、少量的問題，再作此平截面假定就有很大差異，上述的正截面承載力及應力計算方法就不完全適用。因此，將無黏結預應力筋的混凝土梁按有黏結筋梁的計算方法來計算，其平截面假定就有矛盾。

3 計算示例

采用圖1和圖2所示矩形截面簡支梁的施加預應力方法及正截面計算圖示。設簡支梁計算跨徑L=16 m，梁上作用滿跨均布荷載及自重均布荷載集度總和q=10 kN/m，側跨中彎矩：

即彎矩計算值M=320 kN·m。設梁高h=1000 mm，梁寬b=180 mm，體外筋采用2根直徑25 mm的精軋螺紋鋼筋，總張拉力Fp=20 kN，即體外筋的總拉力σpuAp=Fp=200 kN，體外筋重心偏離截面形心下方距離ep=300 mm，距截面受壓邊緣hp=800 mm，設受拉普通鋼筋為4根直徑20 mm的鋼筋，fsdAs=351 680 N，鋼筋中心至截面受壓邊緣距離hs=940 mm。混凝土軸心抗壓強度設計值fcd=20.5 MPa。

3.1 體外筋作為截面承載力計算

按傳統算法，將體外筋作為截面承載力的一部分，即按式（2）計算截面受壓區高度：

即449.45 kN·m>M=320 kN·m。

3.2 體外預加力作為作用效應計算

將體外筋對計算截面產生的彎矩作為作用效應的一部分參與到作用效應組合中。體外筋對計算截面產生彎矩：

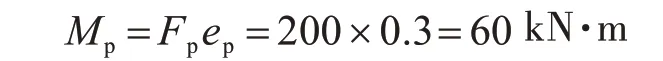
跨中截面作用效應組合設計值：

即彎矩計算值M=Md=260 kN·m，這時計算截面受壓區高度按式（2）計算時，刪除體外筋項：

正截面抗彎承載力按式（1）計算時，刪除體外筋項：

從以上計算結果來看，傳統算法將體外筋作為截面承載力計算時彎矩計算值大，抗彎承載力也大。體外預加力作為作用效應計算時彎矩計算值小，抗彎承載力也小，只是Mu/M不同而已，而且這一比值也無規律性。作者所做體外筋折線形布置的連續梁算例結果也是如此，雖無異樣，但傳統算法解釋不了上述力學現象。體外筋對梁體的接觸點只限于錨固點和轉向點，體外筋就是一種加力的工具，無論有無體外預應力鋼筋，無論采用何種加力工具，只要在接觸點相同位置施加相同的外力，梁的受力效果是一樣的，即使體外筋拉力有變化，也是通過接觸點的等效節點力大小變化對梁產生影響。實際上，現行的規范中［1-4］，在斜截面受剪承載力計算時，表面上將體外筋彎起提供的剪力作為斜截面承載力的一部分，如果將此項移到作用效應一側，實際上也就成為作用效應組合設計值的一部分，只不過再乘以安全系數而已，而且抗剪計算中的縱向鋼筋配筋率和截面有效高度都不計入體外筋。還有現今的混凝土應力計算也是將體外筋對計算截面產生的內力參與到作用效應組合中進行的。其實，這已經將體外筋的作用當成作用效應考慮了。因此，現行研究及規范在正截面抗彎承載力時將體外筋按有黏結筋對待，而在斜截面抗剪承載力計算和正截面應力計算時又按無黏結筋對待，前后不一致。工程設計中，體外預應力筋肯定是無黏結筋，體內預應力筋則不一定是有黏結筋，關鍵看預應力筋與混凝土有無黏結。從以上討論可看出，無黏結預應力筋配筋的混凝土梁，應按文中3.2節的方法進行計算，文中所討論的問題就能解釋清楚。

4 結 論

通過上述的理論和計算示例分析，雖然對正截面抗彎承載力的計算相對看不出什么異樣，但有以下事實：

（1）應將體外預應力筋的對梁產生的內力視為永久作用的一部分，乘以相應的組合參數，參與到作用效應組合中來計算，而不是將體外筋本身作為截面承載力的一部分。

（2）這樣做力學概念清楚，更加符合平截面假定，而且正截面抗彎、斜截面抗剪的承載力計算和正截面應力計算都將體外筋按無黏結筋對待，前后才不矛盾。