MULTIPLE SOLUTIONS OF SOME ELLIPTIC SYSTEMS WITH LINEAR COUPLINGS?

(陳宇彤) (蘇加寶)

School of Mathematical Sciences,Capital Normal University,Beijing 100048,China E-mail:chenyutong@cnu.edu.cn;sujb@cnu.edu.cn

Mingzheng SUN (孫明正)

College of Sciences,North China University of Technology,Beijing 100144,China E-mail:suncut@163.com

Rushun TIAN (田如順)?

School of Mathematical Sciences,Capital Normal University,Beijing 100048,China E-mail:rushun.tian@cnu.edu.cn

Abstract In this paper,we study the existence of nontrivial solutions to the elliptic systemwhere ??RNis bounded with a smooth boundary.By the Morse theory and the Gromoll-Meyer pair,we obtain multiple nontrivial vector solutions to this system.

Key words Morse theory;multiplicity;elliptic system;linear couplings

1 Introduction

In this paper,we consider the system

where ? is a bounded domain in Rwith a smooth boundary,and

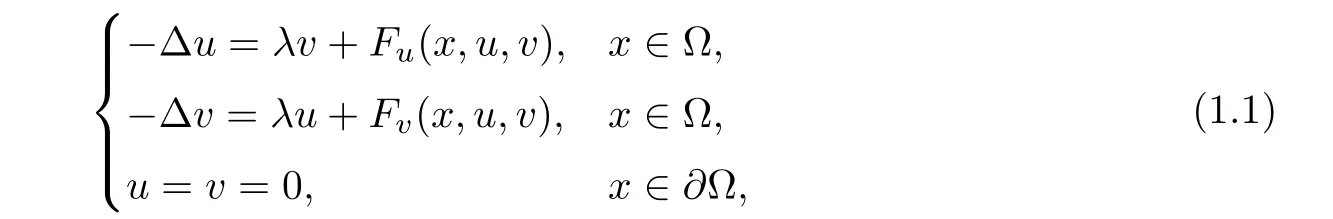
λ

∈R is a parameter.As a concrete example,

F

(

x,u,v

)=

u

,

F

(

x,u,v

)=

v

was considered in[1],and more general power type nonlinearities were studied in[2].Here we are interested in the case in which the asymptotic linear nonlinearities satisfy the Landesman-Lazer type resonance conditions.More precisely,we make the following assumptions on

F

:

A solution of(1.1)is called a nontrivial solution if(

u,v

)/=(0

,

0).If a nontrivial solution has one component identical to zero,then this solution is called semi-trivial,and if

u

/=0 and

v

/=0,then(

u,v

)is called a vector solution.

Remark 1.1

(1)If(

F

)holds,then(1.1)does not have semi-trivial solutions,that is,any nontrivial solution of(1.1)must be a vector solution.(2)The constant

γ

that appears in(

F

)has a lower bound that depends on

M

and ?.Above this lower bound,

γ

is free to take any value.Fixing such a

γ

,(

F

)then requires some

m>

0 such that(1.2)holds.We shall see in Section 3 how such a lower bound is determined.Notice that we just need(

F

)to be valid with one pair of(

γ

,m

).

The main results of this paper are the following theorems:

Theorem 1.2

Assume that

F

satis fies(

F

)

,

(

F

)and(

F

).Then there exists

δ>

0 such that,for any

λ

∈(

λ

?

δ,λ

),system(1.1)has at least three solutions.If(

F

)also holds,then at least two of these solutions are vector solutions.

Theorem 1.3

Assume that

F

satis fies(

F

)

,

(

F

),(

F

)and(

F

).Then there exists

δ>

0 such that,for any

λ

∈(

λ

,λ

+

δ

),system(1.1)has at least three solutions.If(

F

)also holds,then at least two of these solutions are vector solutions.

The main theoretical tools we adopt in this paper are the Conley index,the Gromoll-Meyer pair and the Morse relation;we refer to[6,7]for more on these topics.To the best of our knowledge,[4]was the first paper that applied the Morse theory to the coupled systems.In[22,24]a bifurcation theorem related to Morse indices was applied to the coupled systems with power type nonlinearities.In this paper,we apply the Morse theory to find multiple nontrivial solutions.The above theorems extend the corresponding results in[10]by including features that hold for the system under consideration.

This paper is organized as follows:notations and the properties of an associated linearized system are given in Section 2.In Section 3,we prove the main theorems and give some comments.

2 Preliminaries

By(

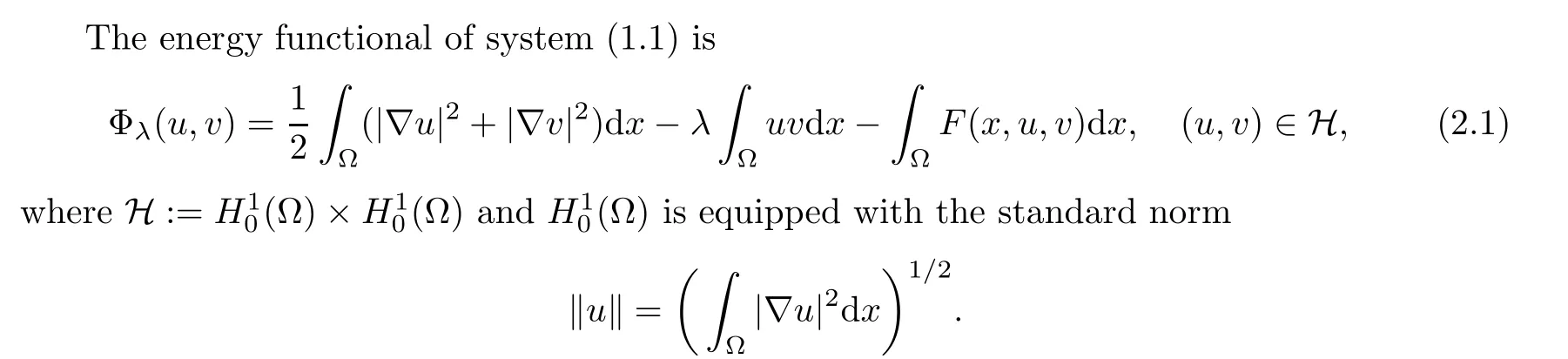
F

),Φis well-de fined and is of

C

in H.We can rewrite Φin the abstract form as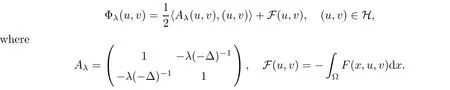

Remark 2.1

System(1.1)can be written as

L

(

u,v

)=

μ

(

u,v

)+(1?

μ

)(

F

,F

),where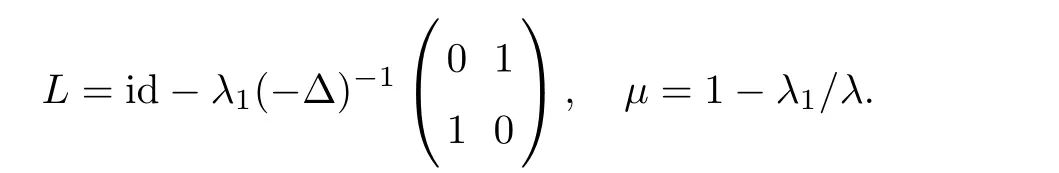

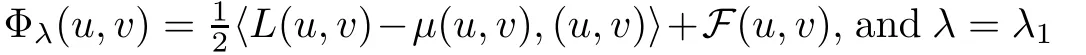
The linearized part of system(1.1)near in finity reads as

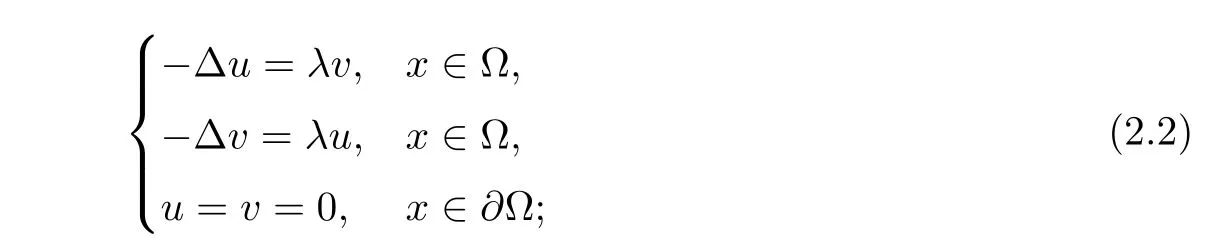
this is related to the eigenvalue problem of the biharmonic operator with Navier boundary conditions.For more references on this,we refer to the monograph[14].If the coefficients of linear coupling terms are independently chosen,that is,(2.2)becomes an asymmetric system

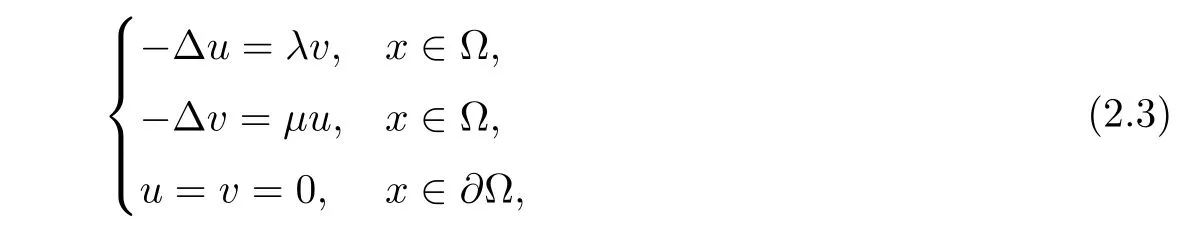
then[23,Lemma 2.1]provides a description as follows:

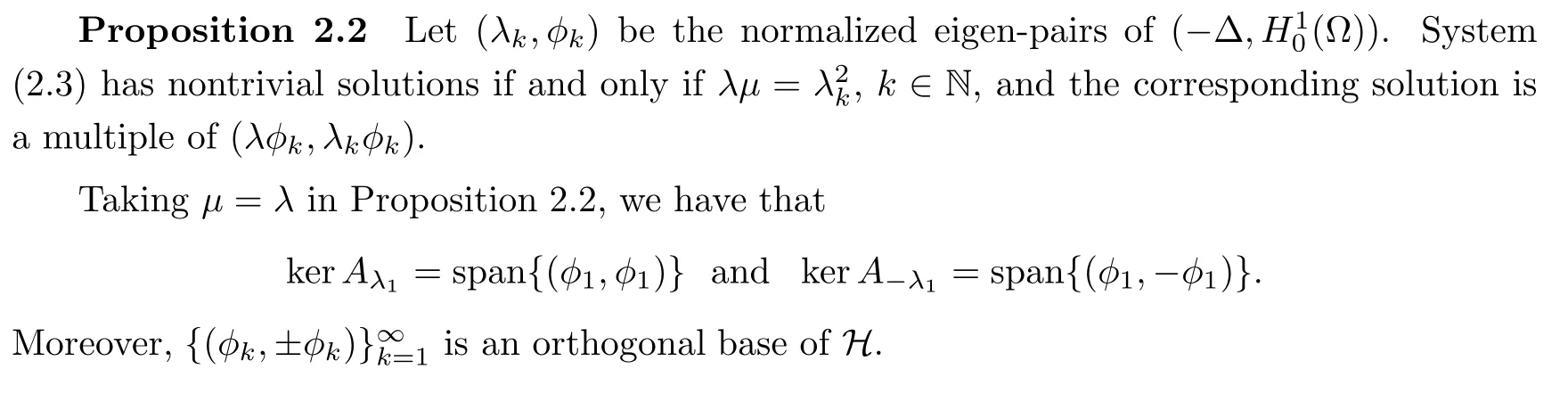
3 Proofs of Theorems 1.2 and 1.3

where the line segment connecting(

T,T

)and(

t,t

)is the selected path.Then,for

t>T

,

Thus,

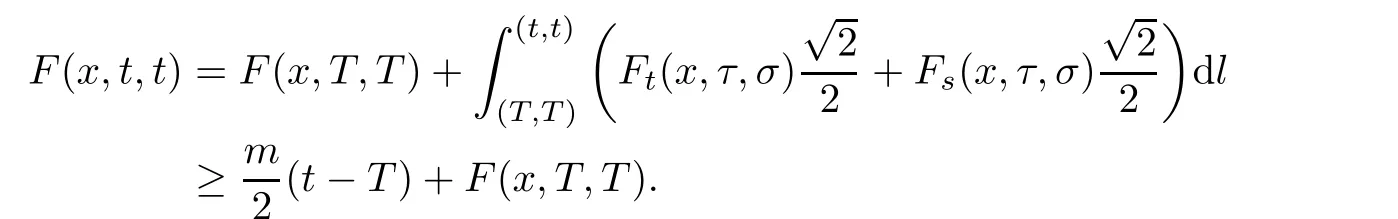
F

(

x,t,t

)→+∞as

t

→+∞.With similar arguments,

F

(

x,t,t

)→+∞as

t

→?∞too.

The next lemma is a generalization of the scalar equation(see[19]).

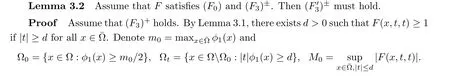
Then a direct c alculation shows that

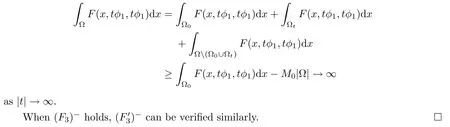
To apply the Morse theory,we need a few lemmas.

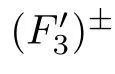
Proof

Letting{(

u

,v

)}be a sequence in H satisfying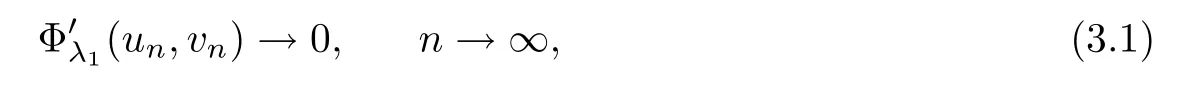

there exists some

C>

0 such that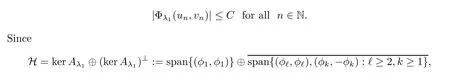

the sequence{(

u

,v

)}has a decomposition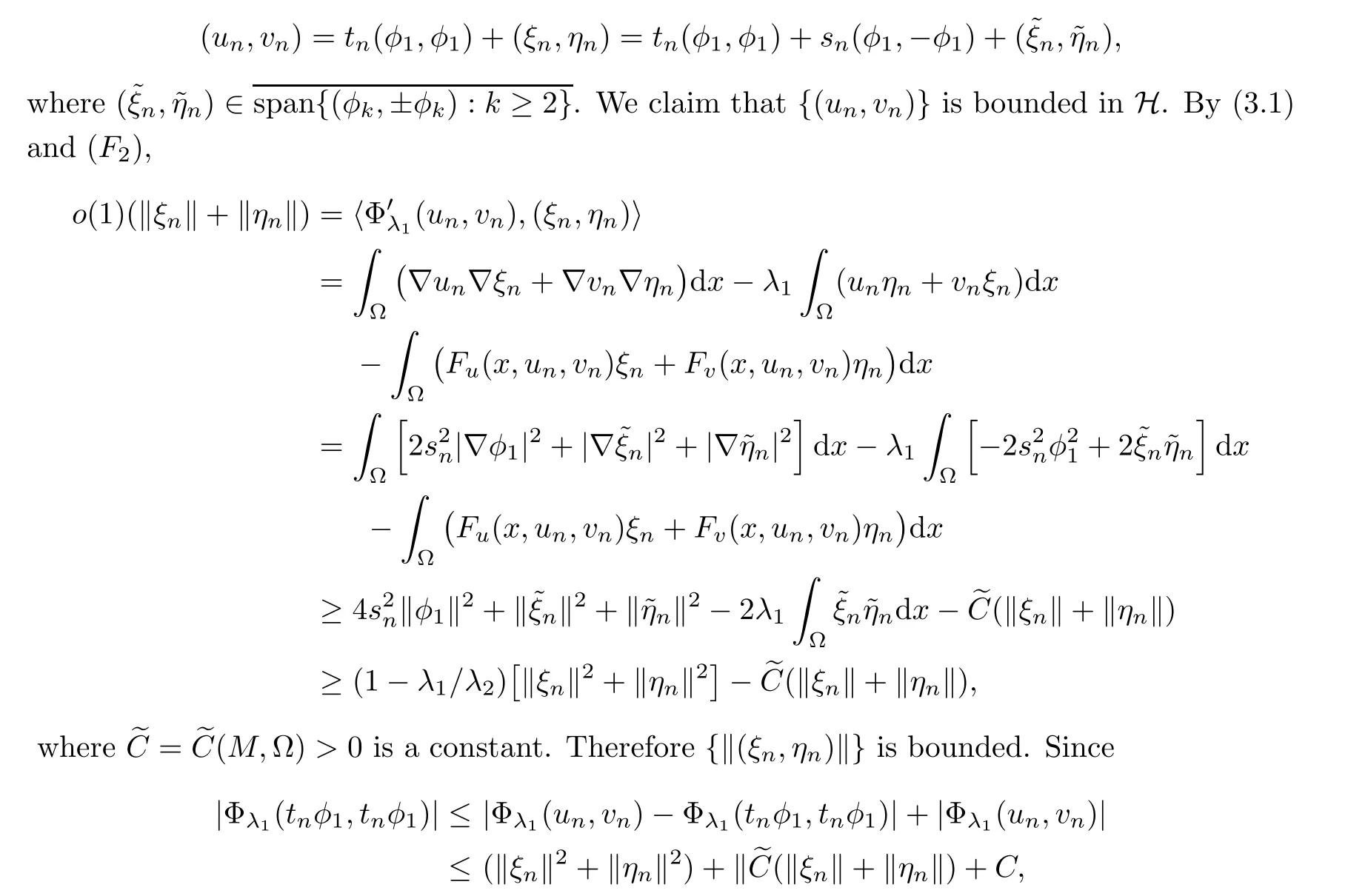

it follows that{Φ(

t

φ

,t

φ

)}is bounded.Therefore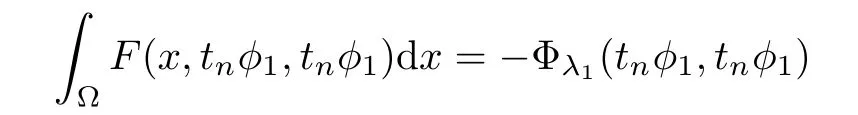

is bounded.By Lemma 3.2,{

t

}is also bounded.Thus{(

u

,v

)}is bounded in H.Therefore,a weakly convergent subsequence exists,so a strongly convergent subsequence can be extracted by using the compact embedding and the equations.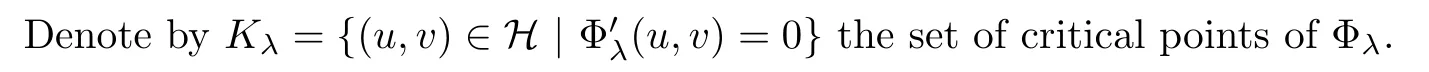

Lemma 3.4

Assume that

F

satis fies(

F

),(

F

)and(

F

).Then

K

is bounded.

Proof

We prove that the case for(

F

)holds.Assume,for the sake of contradiction,that there is a sequence{(

u

,v

)}?

K

such that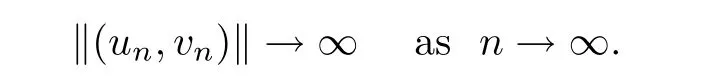

Let(

u

,v

)=

t

(

φ

,φ

)+(

ξ

(

t

)

,η

(

t

))be the orthogonal decomposition of(

u

,v

)in H.Then,by the arguments in the proof of Lemma 3.3,one deduces that{(

ξ

(

t

)

,η

(

t

))}is bounded in H.Since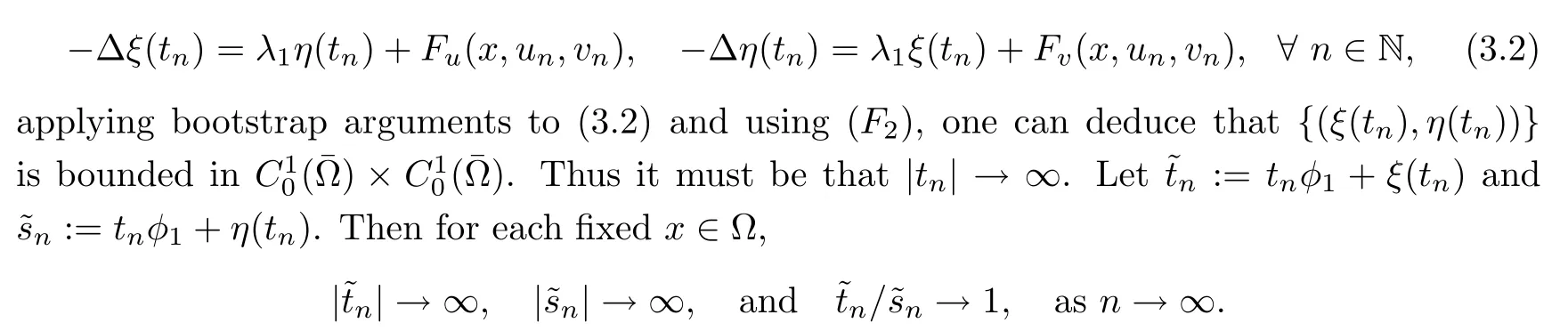

Multiplying the equations of(3.2)by

φ

and integrating over ?,we obtain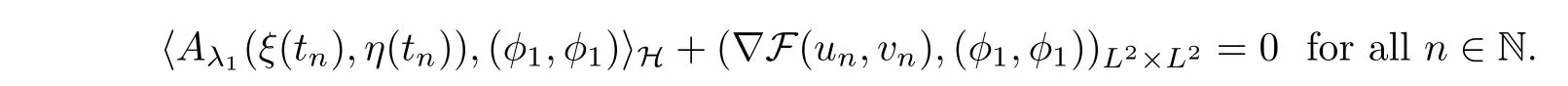

Since ker

A

and(ker

A

)both are invariant subspaces of

A

,the orthogonality implies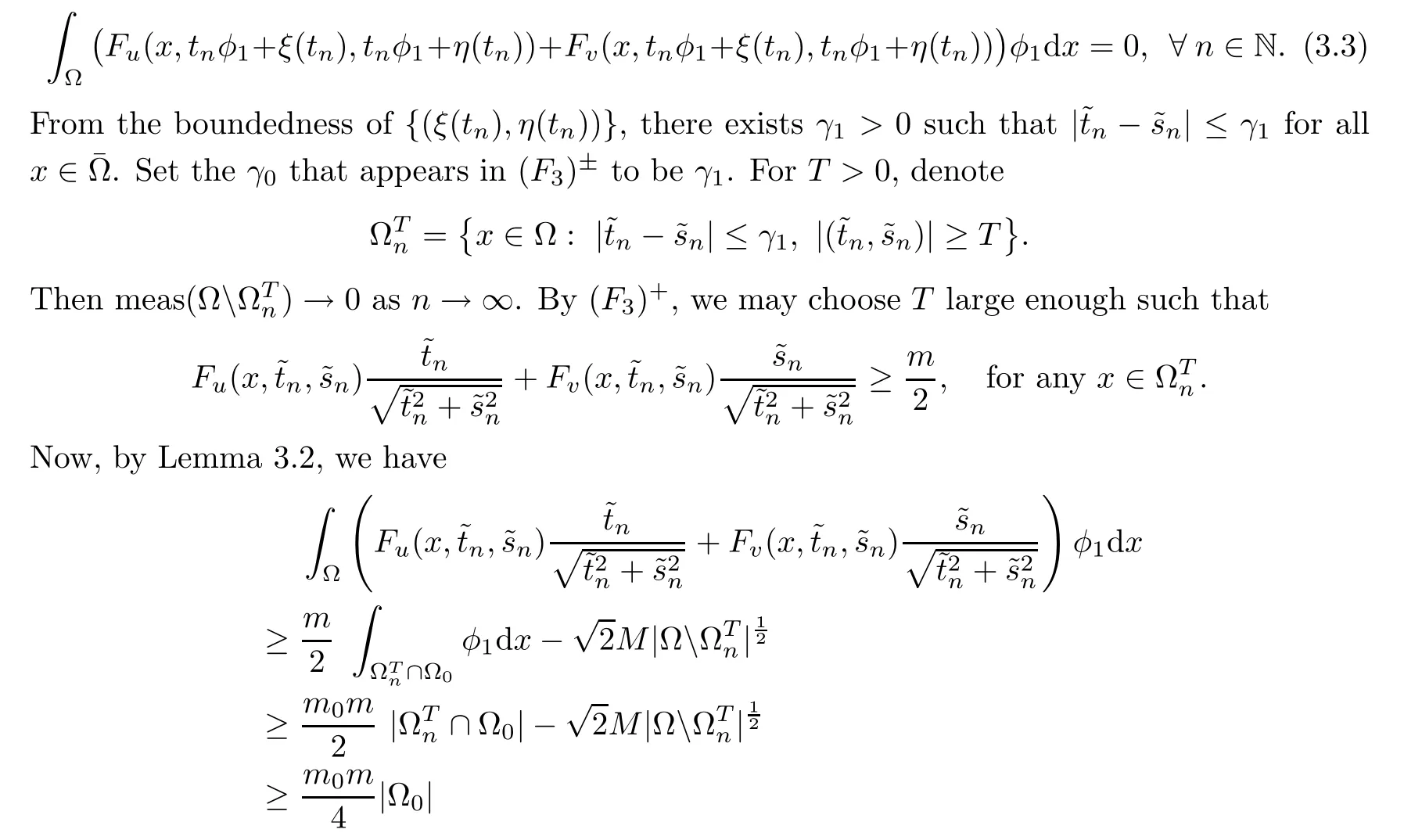

for

n

large enough.By(3.3),it holds that

Now we are ready to present the proofs of Theorems 1.2 and 1.3,which are based on the framework laid out in[10].It is worth mentioning that the system,as compared to the scalar cases,requires different techniques for obtaining multiple solutions.

Next,we prove the existence of multiple solutions to(1.1).We employ the notations and concepts from[5,7,9,10].Let

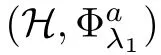
O

be a big closed ball containing

K

,and let

α,β

be regular values of Φsuch that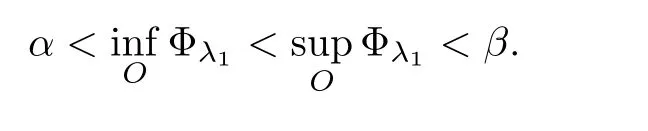

Since Φsatis fies the(PS)condition,by the de finition in[7,9],(

O,α,β

)is an isolating triple f or

K

.De fine

From the boundedness of

K

,there exists a bounded Conley index pair(

N,N

)for

K

.By the topological invariance of the Conley index and the fact that a Gromoll-Meyer pair is also a Conley index pair,we have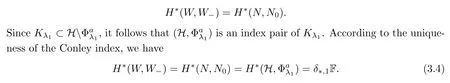

For

δ>

0 small enough and

λ

∈(

λ

?

δ,λ

),Φsatis fies the(PS)condition and(

W,W

)is also a Gromoll-Meyer pair of

K

∩

W

(see[7,9]).It follows from(3.4)that Φhas a critical point(

u

,v

)∈

W

with the critical group

C

(Φ

,

(

u

,v

))/=0.This means that(

u

,v

)is a mountain pass point of Φ([6]).Notice that for each fixed

λ

∈(

λ

?

δ,λ

),

Let

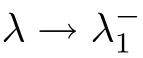
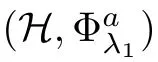
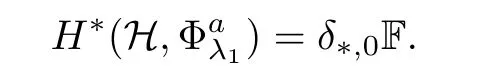
O

be a big closed ball containing

K

,and let

α,β

be regular values of Φsuch that

Then(

O,α,β

)is an isolating triple for

K

and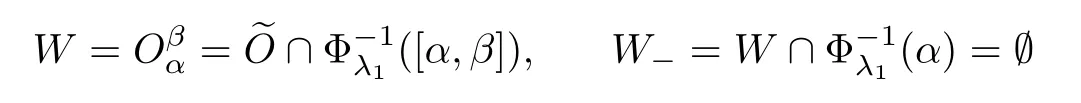

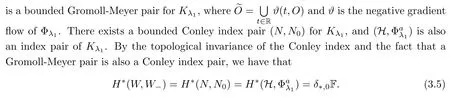
For

δ>

0 small enough and

λ

∈(

λ

,λ

+

δ

),(

W,W

)is also a Gromoll-Meyer pair of

K

∩

W

(see[7,9]).It follows from(3.5)that Φhas a critical point(

u

,v

)∈

W

with the critical group

C

(Φ

,

(

u

,v

))/=0.Thus(

u

,v

)is a local minimizer of Φand

C

(Φ

,

(

u

,v

))=

δ

F.For each fixed

λ

∈(

λ

,λ

),Φis anti-coercive on Hand coercive on H,and we have that Φsatis fies(PS)and that

K

is bounded.For

a<

inf Φ(

K

),

Therefore Φhas a critical point(

u

,v

)such that

We may assume that(

u

,v

)∈

/N

for

δ>

0 small,otherwise a third critical point of Φcould be obtained by comparing(3.5)and(3.6).The linearized system of(1.1)at(

u

,v

)reads as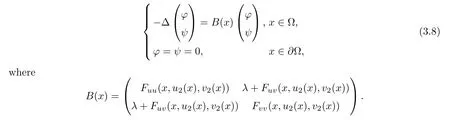

By(

F

),for

δ>

0 small and

λ

∈(

λ

,λ

+

δ

),the matrix

B

(

x

)is cooperative and fully coupled,it follows from(3.7)and[8,Theorem 2.1]that

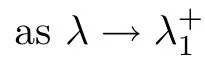
Acknowledgements

The authors would like to thank the referee for giving valuable suggestions and a kind reminder of reference[4].