基于組合權重與TOPSIS法的火力發電廠運行指標評價

林永君，白青飛

（華北電力大學，河北 保定 071003）

0 引言

隨著我國電力體制的改革，“廠網分開，競價上網”的政策使得屬于不同發電企業的發電公司競爭更加激烈，加上新冠肺炎疫情的影響，售電市場的競爭也愈發激烈，眾多發電公司面臨著更多的挑戰和機遇［1］。發電公司如何進行提前規劃，抓住可以充分利用的機遇，占據市場更大的份額，獲得更高的競爭力，以更加科學的方法來運營電廠以獲取更多的利潤，是現實中亟待解決的問題。因此，如果能采取一種科學的方法將多家發電廠的運行指標數據進行比較準確的對比，評價出發電廠指標的優劣性，不僅對發電廠找出自身存在的問題、提高競爭力有很大的幫助，也能縮小發電廠間的差距，推動電力行業的發展，對火電廠節能優化具有重要的意義［2］。

現在對電廠綜合評價的研究已有很多。文獻［3］將改進的TOPSIS 法引入到電廠運營指標的評價上，公正客觀地對電廠運營指標進行評價。文獻［4］利用改進的TOPSIS 法，方便簡便地實現了火電廠混煤摻燒方案的選擇。文獻［5］使用TOPSIS 法、熵值法與層次分析法構建了火電機組綜合評價模型，結果與實際經驗相符，表明該方法適用于機組多指標多方案的評價過程。文獻［6］先是通過層次分析法構建多層次的指標模型，然后計算確定其權重，采用模糊評價方法對火電廠進行綜合評價。

為了綜合考慮主觀權重和客觀權重，對評價方案的指標使用組合權重，本文將熵權法與層次分析法相結合，兼顧主觀和客觀的優點，使主觀權重和客觀權重相融合求出組合權重，再通過TOPSIS 法建立加權規范矩陣和正、負理想解，利用歐式距離和排隊指示值對各火電廠運行指標的優劣進行排名，對各電廠運行指標進行綜合評價，為電廠加強自身建設和提高競爭力提供指導。

1 確定組合權重

1.1 層次分析法確定主觀權重

層次分析法（Analytic Hierarchy Process，AHP）是一種解決多目標復雜問題的層次權重決策分析方法，該方法將定量與定性分析結合起來，利用決策人的經驗判斷各指標的相對重要程度，并合理給出每個方案標準的權重，利用權重求出各方案的優劣次序［7］。層次分析法求主觀權重，先是利用層次結構模型由決策人構造比較判斷矩陣A，再用本征向量法求最大特征值λmax和權重α，最后對矩陣A的一致性檢驗，若最大特征值λmax大于表1 中給的同階矩陣相應的時不能通過一致性檢驗，應重新估算。利用Saaty提出的近似算法求得λmax，過程如下：

表1 k階矩陣相應的臨界本征值

對A中每行元素連乘并開k次方，即為

求得權重為

A中每列的元素求和為

計算λmax的值為

1.2 熵權法確定客觀權重

熵權法是一種客觀的賦權方法，使用的過程中，根據各指標的變異程度，利用信息熵計算出各指標的熵權，再通過各指標的熵權對所有指標進行加權，從而得到比較客觀的指標權［8-9］。對于大多數情況來說，假如某個指標的信息熵越小，則說明該指標的變異程度越大，提供的信息越多，在評價或則決策中起到更大的作用，其權重也就越大。若是信息熵越大，則說明該指標的變異程度越小，提供的信息越少，在評價或則決策中起到比較小的作用，其權重也就越小［10］。熵權法完全根據決策矩陣求出能夠代表權重的熵權，能有效規避專家的主觀判斷對權重分析的影響。現設有m個決策對象，n個決策指標，求各指標值權重的計算過程如下：

計算第i個對象的第j個指標下的指標值Yij的比重為

計算第j項指標的熵值為

計算第j項指標的差異系數為

對于第j項指標來說，指標值xij的差異系數越大，則對方案評價xij的作用就越大，熵值就越小。

計算第j項指標的權重

式中：0＜βj＜1=1。

最后就得到指標權重向量β=(β1，β2，…，βn)T。

1.3 主觀權重和客觀權重融合

通過層析分析法求得的主觀權重｛αj｝和熵權法得到的客觀權重｛βj｝，通過式（9）進行融合，計算出組合權重。

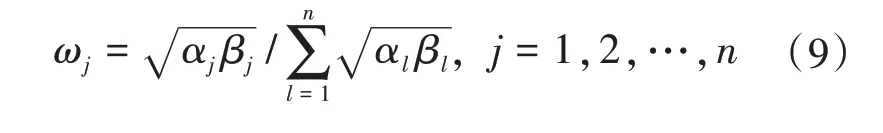
2 基于組合權重的TOPSIS法

TOPSIS 法［11］作為一種對多指標、多方案分析的系統評價方法，通過計算各備選方案與正、負理想解的距離，來確定備選方案與理想解的貼近度，最后并根據貼近度的大小對方案的優劣進行分析評價和排序。正理想解是一個方案集X中并不存在的虛擬的最佳方案，它的每個屬性值都是決策矩陣中該屬性最好的值，而負理想解則是虛擬的最差方案，它的每個屬性值都是決策矩陣中該屬性最差的值［12］。

2.1 初始指標矩陣的建立

設有m個決策對象，n個決策指標，其初始指標矩陣為

2.2 用向量規范化的方法求得規范決策矩陣

設規范化決策矩陣Y=｛yij｝，由初始指標矩陣X可得

1）構成加權規范陣Z=｛zij｝。

由層次分析法和熵權法所得到的組合權重矩陣ω=(ω1，ω2，…，ωn)T乘規范化決策矩陣Y就可得到加權規范陣Z。

2）確定理想解x*和負理想解x0。

理想解x*是一個方案集X中并不存在的虛擬的最佳方案，它的每個屬性值都是決策矩陣中該屬性的最好的值；而負理想解x0的屬性值都是決策矩陣中最差的值，是虛擬的最差方案。設理想解x*的第j個屬性值為，負理想解x0第j個屬性值為，則

歐氏距離（Euclid Distance）是一種采用比較多的距離定義，其表示的意義就是二維或者多維空間中兩個確定點的真實距離。例如二維空間中存在兩個點（x1，y1）和（x2，y2），則歐式距離的表達式d=。TOPSIS 法中就是分別計算各方案到理想解和負理想解的歐氏距離，利用歐氏距離來評判各方案的優劣。

備選方案xi到理想解的距離為

備選方案xi到負理想解的距離為

計算各方案的排隊指示值（即綜合評價指數）

由式（17）可以知道綜合評價指數是用方案到負理想解的距離除以方案到正負理想解距離的和，因為備選方案離負理想解的距離越大越好，所以說綜合評價指數也是越大越好，最后按照的大小排列來評價方案的優劣次序。

3 實例分析

通過在北極星電力網站［13］上查詢的資料，得到了河南省2016年7月份一些電廠主要生產經營指標報表，經過整理選取了其中8 家發電企業的運行指標作為實例來進行分析評價，這8家企業都是2臺機組，裝機容量為1 200 MW，運行指標包括發電量、平均利用小時、發電標準煤耗率、供電標準煤耗率和廠用電率。原始資料如表2所示。

表2 原始數據

基于上述查詢到的資料，利用組合權重和TOPSIS法來計算和評價各電廠運行指標的優劣。

3.1 求得規范決策矩陣

由初始指標矩陣可以得知一共有8 個決策對象，5個決策指標，8個對象分別用數字1—8來表示，5個決策指標分別用A、B、C、D、E來表示。由初始指標矩陣計算規范決策矩陣，數據如表3所示。

表3 規范決策矩陣Y數據

3.2 計算各指標的比重

根據式（5）由規范決策矩陣計算第i個對象的第j個指標下的指標值的比重Pij，結果如表4所示。

表4 第i個企業第j個指標占該指標的比重

3.3 計算主觀權重、客觀權重及組合權重

通過2.1 和2.2 中的方法，分別求出主觀權重和客觀權重，再由式（9）求得最后的組合權重，計算結果如表5 所示。通過式（12）計算得到系統的加權規范陣，結果如表6所示。

表5 各指標的權重

表6 加權規范陣數據

3.4 確定正負理想解以及各方案與正負理想解的歐氏距離

由原始資料可知，運行指標中發電量和平均利用小時是效益型屬性，越多越好，發電標準煤耗率、供電標準煤耗率和廠用電率是成本型屬性，越小越好。因此得到的理想解為x*=（0.177 7，0.296 1，0.007 53，0.006 73，0.027 9），負理想解為x0=（0.080 6，0.106 4，0.007 99，0.007 13，0.039 2）。

由式（15）、（16）計算各個方案到正、負理想解的歐氏距離，結果如表7所示。

表7 各個方案到正、負理想解的歐氏距離

3.5 計算各方案的排隊指示值（即綜合評價指數）

通過式（17）計算出各方案的綜合評價指數，結果如表8所示。

表8 各方案的綜合評價指數

4 結語

將層次分析法、熵權法與TOPSIS 法相結合，對八家電廠的機組運行指標進行綜合評價。通過查詢到的數據，將熵權法計算得到的客觀權重，與層次分析法計算得到的主觀權重相融合，得到組合權重，最后結合TOPSIS 法，使用正、負理想解和歐式距離求得各方案的排隊指示值，來綜合評價各電廠運行指標的優劣。研究表明組合權重與TOPSIS 法對火力發電廠的運行評價指標是可行的，過程簡單、快捷，給電廠的實際運行提供指導。