高艷艷，陳秀鋒，曲大義，陳 偉

(青島理工大學 機械與汽車工程學院，青島266525)

隨著我國經濟水平的提高，汽車保有量迅速增加，城市交通擁堵接踵而至。及時、準確地提供道路交通狀態信息，出行者可以根據有效信息選擇合適的交通工具以及出行時間點；交通組織者可以獲取實時道路交通狀態，采取交通控制和誘導對策，從而有效提高城市出行效率，緩解路網交通擁堵。

目前，交通狀態判別主要從兩方面開展：判別指標、判別方法。城市道路交通狀態的判別指標主要有流量、速度、占有率、密度和平均延誤等[1-3]，關偉等[4]對不同密度下的交通速度分布特性進行綜合分析，最終把一個城市道路交通流劃分為4種狀態；戴學臻等[5]選取的判別指標為車輛平均行程車速、道路網延誤時間比，利用集對化的分析方法與三角模糊化函數方法進行實時耦合，構建了城市道路交通運行狀態識別模型；黃艷國等[6]選擇了3個樣本數據信息：流量、速度、占有率，并明確提出了一種道路交通運行狀態實時化的判別分析方法，這種判別方法采用的是模糊C均值聚類算法。K-means聚類算法是判斷城市道路狀況最常用的方法之一，然而，由于聚類數的確定難度大，對初始聚類中心選擇更是無統一標準，最終導致交通狀態判別結果與實際城市交通狀態不相匹配，這就需要對聚類數和聚類中心進行優化。針對這些問題，FAYYAD U等[7]明確提出選擇多次迭代來更新采樣數據以獲得初始值，從而解決K-means算法嚴重依賴于初始聚類中心選擇的問題；卞彩峰等[8]采用粒計算，這一算法屬性分辨能力較強，利用這一優點，使聚類有效性函數對屬性值依賴降低，最終獲取最佳聚類數。

交通流參數選取具有一定的隨機性，往往會影響判別結果的準確性。K-means聚類算法在一定程度上取得了實際效果，不過只是對聚類數和初始聚類中心進行單一優化，并未將兩者結合在一起，仍存在一定的不足。本文利用因子分析方法，對多個變量進行相關性分析，選取出合適的交通流參數，作為交通判別指標，并結合改進K-means聚類算法，探究交通流的運行情況，從而對城市快速路交通狀態進行判別。

1 數據采集及指標的選取

1.1 數據的采集與處理

本文所研究的對象是某城市約10 km快速路，交通流數據由兩部分組成：①感應線圈檢測器進行采集分析得到，包括流量q、速度v、占有率o。數據采集時間為某一個工作日0：00—24：00，每次數據采集時間間隔為5 min。該路段上某一截面命名為S，共有4條車道，每條車道上各有一個感應線圈檢測器，分別為S1，S2，S3，S4。數據類型如表1所示。②行程時間t數據，利用Vissim仿真軟件，根據實測數據進行標定得到。

表1 數據類型

感應線圈檢測器共收集原始數據852條，缺失12條，為了保證結果更加準確，現需要將缺失數據進行補充完整，數據具體處理方法如下：

1) 缺失數據的補充。由于本文數據僅缺失12條，屬于少量數據缺失范疇，數據采集時間間隔較短，所以行駛狀態不會發生太大的變化，基于以上特性，為保持數據的完整性，同時也要求計算簡單，收斂性好，故采用分段線性插值法對數據進行補充。

分段線性插值法采用的函數是分段線性插值函數，用直線將兩個相鄰的數據點連接。要求一個點的數值，假設與其相鄰的兩個節點是(xm,ym)和(xn,yn)，具體求值方法如式(1)所示。

(1)

2) 數據的合成。本文數據是由4個車道所測數據組成，需要將每個車道上的數據合成為一個截面的數據[9]，合成數據方法如式(2)所示。

(2)

式中：qe為截面e的流量；ve為截面e的速度；oe為截面e的占有率；f為車道編號；m為截面車道數。

1.2 交通流參數的選取

交通流參數的選取和算法的應用效果密切相關，選擇的交通參數要能夠準確反映交通狀態變化規律。結合交通流數據來源以及特點，本文選取8個交通流參數，分別為流量q、速度v、占有率o、密度k、行程時間t、飽和度s、占有率/流量(o/q)、占有率/速度(o/v)，其中q，v，o通過合成公式(2)計算得到，k，s，o/q，o/v在原有數據基礎上，通過計算和處理得到，行程時間t由Vissim仿真獲得。

2 因子分析

所謂因子分析，就是保持原有信息不發生任何的變化，將具有相同特性的變量劃分到同一個因子中，實現數據的簡化、指標的降維，從而簡化因子分析過程[10]。

2.1 因子可行性驗證

本文采用KMO(Kaiser-Meyer-Olkin)和Bartlett球形(Bartlett's Test of Sphericity)兩種檢驗方法，檢驗8個交通流參數是否適合因子分析[11]。使用Spss軟件進行檢驗，結果如表2所示，KMO結果為0.790>0.6，表明8個交通流之間存在較好的相關性。Bartlett球形假設檢驗顯著性為0，拒絕零假設，表明相關系數矩陣不是單位陣，適合進行因子分析。

表2 KMO和Bartlett檢驗結果

2.2 主因子的提取

主因子提取通常采用不小于85%的累積方差貢獻率來確定主成分的數量。如表3所示，前2個主因子累積方差貢獻率為98.052%，大于85%，符合判斷標準。因此，選取前2個主因子進行分析。

表3 各因子解釋原有指標總方差情況

表4所示為因子載荷矩陣，顯示出2個主因子在8個交通流參數上的載荷，通過分析得出以下個結論：

表4 主成分載荷矩陣

1) 主因子1與8個交通流參數的相關性均在0.8以上，此數據顯示，主因子1與各交通參數都具有很強的相關性。無論是負相關還是正相關，為了符合實際，需進行因子旋轉。

2) 主因子2與q、s、o/q相對于其他指標具有較強的相關性。

2.3 因子旋轉

本文采用凱撒正態化最大方差法對2個主因子進行因子旋轉。表5所示為因子旋轉后主因子1，2對8個交通流參數的載荷。

由表5可知，旋轉后的主因子1與q，v，o/v相關性較大；旋轉后的主因子2與8個交通參數指標相關性還是很弱，綜合考慮，剔除主因子2，僅保留主因子1。綜上所述，因子分析從8個交通流參數中最終提取出q，v，o/v3個交通參數作為交通狀態判別指標。

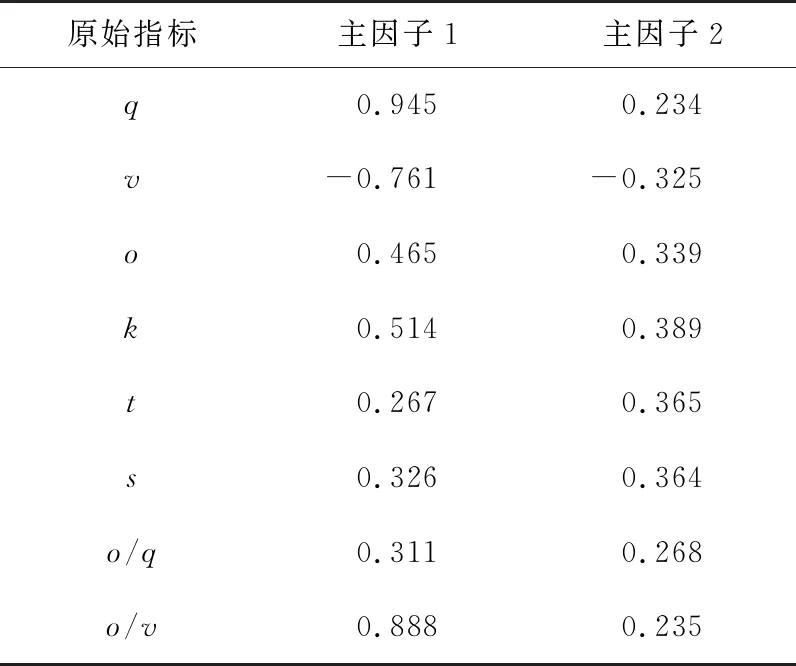
表5 旋轉后的因子載荷矩陣

3 基于改進K-means聚類的交通狀態判別

3.1 改進K-means聚類算法

K-means聚類算法根據樣本之間的距離或相似度，把相似度高、差異小的樣本聚類為一類，最后形成多個類別，使得同一個類別內的樣本具有高相似度，不同類別間差異性大，聚類速度快，方法簡單。但傳統的K-means聚類算法仍存在一定不足：①聚類數K很難確定；②初始聚類中心選取隨意。為了解決以上問題，本文提出了一種改進K-means聚類算法。

改進K-means聚類算法的思路如下：假設要將n個樣本數據Y={Yi|i=1,2,...,n}劃分為K類，用B={Bj|j=1,2,...,K}分別表示K種交通狀態，C1點為首個初始聚類中心點，C={Cj|j=2,3,...,K}為后續初始聚類中心。

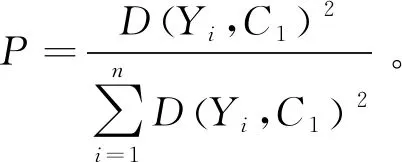
Step3：求出每個數據與初始聚類中心的距離D(Yi,Cj),i=1,2,...,n,j=1,2,...,K，根據求出的距離，按照距離最短原則，將每個數據歸到相應的類別中，即滿足D(Yi,Cj)=min{D(Yi,Cj)}，則Yi∈Zj；

Step7：通過指標值比較選擇最佳的K值，使IDB指標達到最優；

Step8：輸出最優聚類數K以及滿足聚類準則函數收斂性的K個聚類集。

3.2 交通狀態分類及判別效果分析

將改進K-means算法應用到處理好的289組交通流參數數據中，通過因子分析提取q，v，o/v3個判別指標，計算出初始聚類中心，最后輸出最佳聚類數K=4，如表6所示，參照相關已有研究成果將交通運行狀態命名為自由流狀態、穩定流狀態、擁擠流狀態和阻塞流狀態[12]。

表6 初始聚類中心

使用Spss軟件對數據進行交通狀態判別分析，選取初始聚類中心，設置K=4，經過16次迭代，聚類中心的變化可忽略不計時，從而達到聚合的目的，將所有的數據劃分為4類。表7所示為最終聚類中心。圖1所示為截面S通過Spss檢驗最終得到的全天24 h交通狀態判別結果，圖2所示為Origin繪制的4種交通狀態下的交通流基本參數關系。

表7 最終聚類中心

圖1 截面S交通狀態判別結果

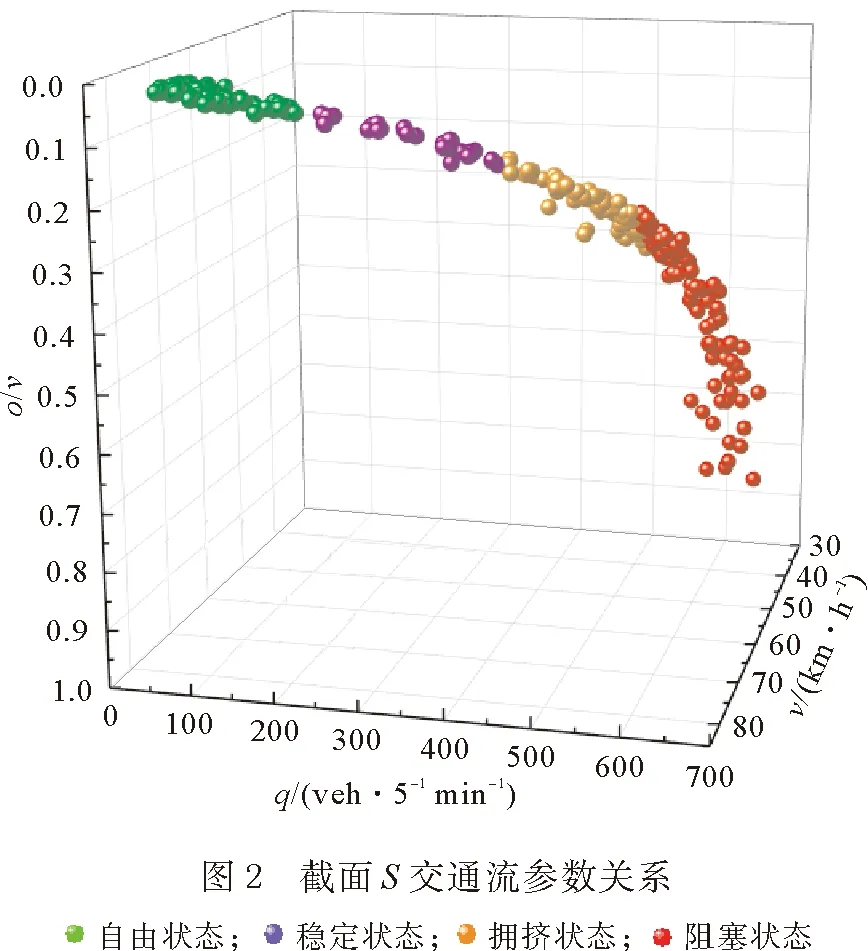
圖1縱軸1—4分別代表自由流狀態、穩定流狀態、擁擠流狀態、阻塞流狀態，數據共有289組。其中自由流狀態為94組，占比32.53%；穩定流狀態為88組，占比30.45%；擁擠流狀態為28組，占比9.69%；阻塞流狀態為79組，占比27.34%。由圖1、圖2可知，該快速路道路狀況基本暢通，大多數擁堵主要集中在早晚高峰，說明本文方法能有效地對交通運行狀態進行分類，且與實際狀況相符。

3.3 對比分析

本文以判別率和誤判率為指標，根據上述獲取的交通流數據，分別使用傳統K-means算法和改進K-means算法對其進行交通狀態判別，與道路實際運行狀況相比，得到4種交通狀態下的判別率和誤判率，如表8所示。

從表8可以看出，在4種交通狀態下，改進K-means算法判別率為97.21%，誤判率為0.74%，其判別精度比傳統K-means算法提高了8.13%，誤判率降低了1.05%。由此可見，改進K-means算法可獲得較好的判別效果，在交通狀態判別上具有一定的優勢。

表8 交通狀態判別效果對比 %

4 結論

1) 傳統交通狀態判別指標的選取都是按照一定的標準和規定，進行直接選取，本文采用因子分析，從q，v，o，k，t，s，o/q，o/v8個交通流參數中，提取出q，v，o/v最為適合的3個交通狀態判別指標。減少交通流參數的選取對算法應用效果的影響，更好地呈現交通狀態變化規律。

2) 改進K-means聚類算法創新點在于建立了交通狀態判別綜合評價函數，將聚類數K和初始聚類中心同步進行優化。

3) 本文將因子分析與改進K-means聚類算法相結合在一起，通過實例驗證，這種方法對快速路交通運行狀態可以有效判別。