方柱微結構表面熔渣接觸角的數值模擬研究

李立鴻，陳 豪，張澤飛，白 皓

1.汕頭華興冶金設備股份有限公司，廣東 汕頭 515063；2.饒平粵興銅加工有限公司，廣東 潮州 515726；3.北京科技大學 冶金與生態工程學院，北京 100083

鋼鐵生產中一些生產設備會受到高溫熔渣的熔蝕，導致設備損壞[1].因此，降低熔渣對生產設備的熔蝕危害可提高設備的壽命.目前，可以采用涂覆陶瓷涂層的方法對設備進行高溫防護.根據液固界面潤濕理論[2]，可考慮通過降低陶瓷涂層對熔渣的潤濕性，減少熔渣在表面的停留，避免熔渣對設備表面的熔蝕，進而提高設備的壽命.目前降低液體潤濕性的方法有兩種，一種是在表面修飾低表面能物質，另一種是在固體表面制備微觀粗糙結構.常用的低表面能物質使用溫度在500 ℃以下，但設備工作環境在1000 ℃以上，而表面制備粗糙結構不受溫度限制，因此可通過在涂層表面構造粗糙結構的方式降低涂層對熔渣的潤濕性.

Young[3]提出了光滑表面上的液體潤濕方程，但實際表面都存在粗糙度，Wenzel[4]和Cassie[5]根據Young提出的潤濕理論，分別提出了在粗糙表面上的潤濕模型，模型如圖1所示.

圖1 潤濕狀態模型

Wenzel假設液體在均相粗糙表面上總是能夠潤濕粗糙結構間的凹槽，并提出了粗糙因子r，推導得到了液體在固體表面的表觀接觸角與粗糙因子及固體表面本征接觸角之間的表達式，即cosθc=r·cosθa.式中θa為固體表面本征接觸角，θc為粗糙表面的表觀接觸角，r為粗糙表面實際固液接觸面積與投影面積的比值.Cassie認為表面由多種組分組成或液體不能完全潤濕粗糙表面時，Wenzel方程將不再適用.當表面粗糙程度達到某一值時，液體不會完全充滿凹槽，此時的固液界面由空氣和固體構成，基于此假設Cassie推導得到潤濕方程，即cosθc=f·cosθa+f-1，其中f為微結構上固液接觸面積分數.潘貽芳等人[6]采用靜滴法，研究了轉爐渣與爐襯耐火材料的潤濕性，解釋了爐渣與耐火材料的粘附機制.程禮梅等人[7]總結了高溫體系常見界面張力與接觸角測量方法，并分析了溫度與熔渣成分對熔渣潤濕性的影響.

目前，關于熔渣在微結構表面潤濕性能的相關研究報道較少.通過ANSYS Fluent二維數值模擬得到熔渣在方柱結構上的表觀接觸角，并與現有的接觸角預測方程進行對比分析，為金屬基陶瓷涂層的疏渣微結構的設計提供指導意義.

1 數值模擬

1.1 VOF模型及控制方程

目前界面追蹤方法常用的有VOF法[8]、LBM法[9]、PIC法和兩相流水平集法等，本研究采用Fluent軟件中的VOF(Volume of Fluid)方法進行數值模擬.VOF法是通過相函數表示各相體積所占單元網格體積的比值，進而確定相界面的位置，該模型適用于追蹤幾種互不相溶合的流體界面，適用于自由表面流動、射流等.

VOF模型中，假設各單元中第i相體積分數為αi，則有：αi=0，單元中無i相；0<αi<1，單元為混合相；αi=1，單元全部為i相.

(1)

通過求解關于體積分數的連續性方程對氣體與熔渣接觸面的捕捉，體積分數的連續性方程微分形式：

(2)

動量方程微分形式如下，式(3)中Fj為包含表面張力及壁面粘附作用的源項.

(3)

1.2 物理模型

本次模擬研究熔渣在具有不同方柱微結構涂層表面靜態接觸角的變化.將物理模型進行簡化，即在方柱結構頂端放置一滴與頂端相切的熔渣，在重力作用下熔渣下落.模擬采用二維模型，計算區域尺寸為5 mm×5 mm，液滴直徑為2 mm，其中a為方柱的邊長、b為微結構間距、h為微結構高度，物理模型如圖2所示.

圖2 物理模型

由于受到陶瓷涂層表面方柱結構加工工藝限制，方柱結構達到微米及亞微米級別較為困難，因此模擬時采用實際加工易于實現的方柱結構尺寸.選取方柱邊長a=200 μm，高度h=150 μm，方柱間隔b選取五種不同的尺寸，定義k為方柱邊長與方柱間隔之比，具體的方柱尺寸如表1所示.

表1 方柱結構尺寸

1.3 熔渣成分及物性參數

模擬采用的熔渣是較為常用的高溫熔渣，模擬中氣體介質為空氣.熔渣的成分和含量及物性參數分別列于表2和表3.由表3可知，陶瓷材料表面能約為0.1 N/m，高溫熔渣的表面能要遠大于陶瓷材料表面能.根據表面潤濕理論，高溫熔渣在光滑涂層表面的本征接觸角應大于90 °，為此模擬時設置5個不同的本征接觸角，5個本征接觸角分別為90，100，110，120和130 °.

表2 熔渣成分

表3 熔渣物性參數

1.4 計算模型

計算域頂部采用普通無滑移壁面，下壁面為方柱微結構表面，左側為壓力入口邊界條件，右側為壓力出口邊界條件.模擬時設置熔渣置于微結構的涂層表面并與之相切的位置，熔渣在重力的影響下降落，最終達到穩定狀態.圖3為計算域和邊界條件的示意圖.

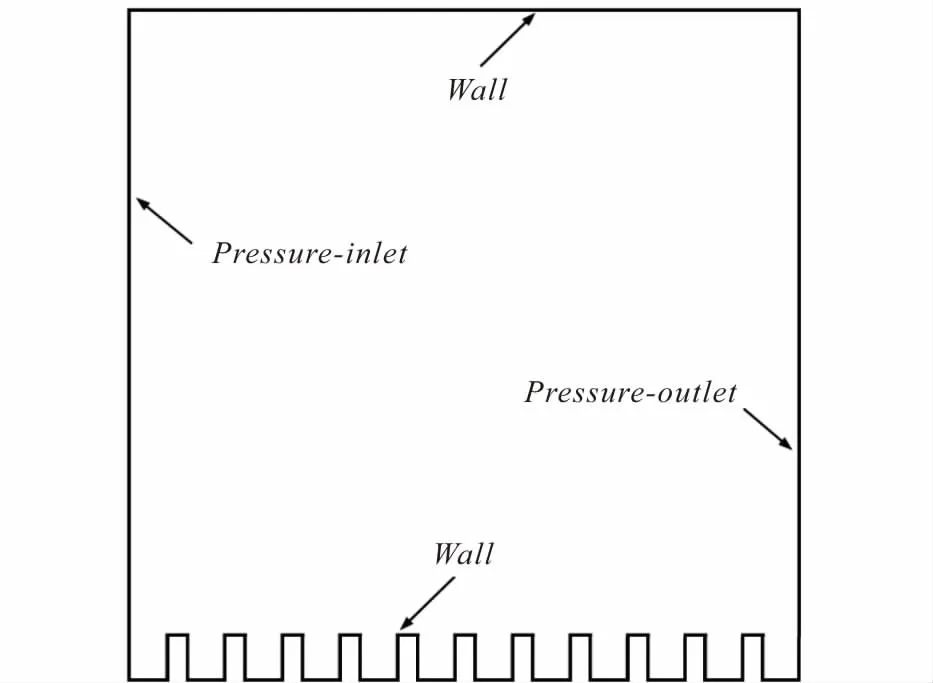
圖3 計算域及邊界條件示意圖

1.5 模型驗證

計算渣滴在具有方柱結構的涂層表面上的接觸角前，需要對計算模型進行驗證.驗證模型采用光滑涂層平面進行驗證，將5個本征接觸角的值，在VOF模型中分別設置為光滑壁面與渣滴的接觸角，其余邊界條件與上述邊界條件保持一致，計算完成后，測量熔渣與光滑壁面的接觸角，進而判斷計算模型是否可以使用.圖4為熔渣在光滑壁面穩定后的形態.

圖4 光滑表面熔渣接觸角

對熔渣在光滑表面穩定后的形態進行測量，并與熔渣在光滑涂層表面的本征接觸角比較，計算模型的誤差值列于表4.

表4 模型誤差值

由表4可知，使用VOF模型模擬熔渣在不同本征接觸角的光滑涂層表面時，熔渣穩定時表觀接觸角的誤差控制在3.5%以下，這說明使用VOF模型模擬熔渣在方柱微結構涂層表面的表觀接觸角是可行的.

2 結果與分析

對熔渣在不同k值的方柱微結構涂層表面上的形態進行模擬，得到熔渣在不同本征接觸角的方柱結構涂層表面的穩定形態，其穩定形態如圖5～圖9所示.從圖5～圖9可以看到，熔渣在方柱結構上穩定后，方柱間隔內充滿空氣，熔渣保持在Cassie潤濕狀態.

圖5 本征接觸角為90°，各k值下熔渣在方柱結構表面穩定形態

圖6 本征接觸角為100 °，各k值下熔渣在方柱結構表面穩定形態

圖7 本征接觸角為110 °時，各k值下熔渣在方柱結構表面穩定形態

圖8 本征接觸角為120 °時，各k值下熔渣在方柱結構表面穩定形態

圖9 本征接觸角為130 °，各k值下熔渣在方柱結構表面穩定形態

將模擬結果與Cassie潤濕狀態接觸角推導方程[12]所計算得到的表觀接觸角進行對比，表觀接觸角方程如式4所示.各本征接觸角的對比結果及模擬誤差值列于表5.

(4)

由表5可知：在涂層方柱結構表面上，熔渣穩定保持在Cassie潤濕狀態，且熔渣的表觀接觸角相比光滑涂層表面均增大；模擬結果與推導方程預測的接觸角值較為符合，誤差在10%以下.表觀接觸角作為衡量固體表面疏液性能的重要指標，涂層方柱結構表面熔渣表觀接觸角的提高，說明了在本征接觸角θa≥90 °的涂層表面，方柱結構可以降低陶瓷涂層對熔渣的潤濕性，提高了涂層疏渣性能.

表5 表觀接觸角模擬計算結果與方程計算結果的誤差表

目前，水在固體微結構表面潤濕性的理論研究[13]及制備方法[14-16]均發展較為成熟，但對熔渣在微結構表面潤濕性研究較少,這是由于熔渣本身具有高溫性，目前的研究手段限制了對其潤濕性的研究.熔渣與水相比，熔渣具有較高的表面張力和粘度.從理論上分析，熔渣的高表面張力和高粘度會使得熔渣在方柱微結構表面的接觸角增大，且從模擬結果來看熔渣接觸角均增大，與經典理論潤濕模型的預測值較為符合.因此，在涂層表面構建方柱微結構的應用可以基于理論模型和模擬結果，對涂層表面構建方柱微結構進行指導，以期提高涂層表面的疏渣性能，改善熔渣熔蝕高溫工作設備，損害設備壽命的問題.

3 結 論

針對鋼鐵企業中生產設備受到熔渣侵蝕的問題，以Wenzel和Cassie潤濕模型為基礎，使用Fluent中VOF模型對熔渣在不同本征接觸角及不同方柱間隔的涂層表面上的接觸角進行了二維數值模擬，對比分析了接觸角方程計算得到的接觸角與模擬得到的接觸角之間的誤差.

(1)模擬計算結果顯示，在具有方柱結構的涂層表面熔渣均處于Cassie潤濕狀態.

(2)熔渣在方柱結構的涂層表面上，表觀接觸角相比光滑表面的均增大；

(3)模擬結果與接觸角方程計算結果對比后發現，模擬結果較為符合方程計算結果，這將為陶瓷涂層表面方柱結構尺寸選擇提供了重要理論依據.