超精密全口徑拋光機氣浮轉臺的靜態特性

安 磊，王 偉*，廖德鋒

（1. 電子科技大學 機械與電氣工程學院，四川 成都 611731；2. 中國工程物理研究院 激光聚變研究中心，四川 綿陽 621900）

1 引 言

拋光工藝作為一種高面形精度的加工工藝，廣泛應用于全口徑超精密平面光學元件的加工中［1-2］。與傳統的機械接觸或液體支承相比，氣體靜壓支撐具有摩擦小、無污染、精度高、壽命長等優點，因而適合應用于超精密全口徑拋光機轉臺。氣浮轉臺利用有壓力的氣體在基座和轉臺間形成一層氣膜，從而將兩者分開，并利用氣體靜壓原理形成承載［3-7］。

國內外學者在靜壓支撐方面做了大量研究。崔海龍等［8］基于流體力學和固體力學的基本控制方程，建立小孔節流空氣靜壓軸承雙向流固耦合數值模擬模型，獲取了設計參數對承載力和剛度的影響規律。李一飛等［9］基于fluent 研究了供氣小孔尺寸、氣腔尺寸、氣膜厚度以及供氣壓力等參數對靜壓軸承承載力和剛度的影響，為工程設計提供了一定的參考。趙曉龍等［10］采用FDM（有限差分法）和超松弛迭代法對變截面節流器的空氣靜壓軸承模型進行求解，指出變截面節流器的設計方法能夠有效提高空氣靜壓軸承的靜態 特 性。Belforte 等［11］基 于FDM 分 析 了 不 同 結構的均壓腔對支撐表面壓力分布、氣體流量和剛度的影響。Lo 等［12］和Liu 等［13］基于FDM 分析了靜壓軸承的壓力分布、承載力以及體積流量率等靜態特性。文獻［14-17］分析了節流器布局、尺寸、形狀以及運行參數如供氣壓力等對靜壓軸承靜態特性的影響。Abdurrahim 等［18］基于FDM 和DTM（微分變換法）分析了不同軸承傾斜下的氣膜厚度、壓力分布和承載力，Shi 等［19］在此基礎上研究了不同轉速和轉子傾斜下軸承的靜態特性。熊萬里等［20］和劉志峰等［21］分析了不同傾斜狀態下液體靜壓軸承油膜的承載特性。

可見，以往的研究較多地關注結構參數和氣源參數等對氣浮支撐的氣膜厚度、壓力分布、承載力等靜態特性的影響，對于角擺和轉速的影響也較多的集中于靜壓和油膜軸承。氣浮轉臺的尺寸和質量較大，工作時轉臺處于懸浮狀態，在制造誤差、偏載等因素的影響下會存在傾斜角擺。角擺和轉速的存在會導致氣膜流場發生變化，從而影響氣膜壓力分布和承載力，導致轉臺動態旋轉軌跡發生改變，致使超精密光學工件的形狀誤差，表面質量等出現變化，從而不能達到使用要求。學者在研究氣浮轉臺靜態特性時，對于角擺和轉速效應的影響關注較少，相關研究并不多見。本文基于柱坐標系下的雷諾方程和流量平衡方程，結合考慮角擺后的氣膜厚度方程采用FDM 進行數值求解，研究單個角擺、組合角擺和轉速對氣膜厚度、氣膜壓力分布以及承載力這些靜態特性的影響。

2 全口徑拋光機氣浮轉臺結構與流體潤滑分析數學模型

2.1 氣浮轉臺結構

圖1 為全口徑拋光機氣浮轉臺結構簡圖，高壓氣體經節流小孔進入均壓腔，進而進入基座和轉臺間，形成環形氣膜，利用靜壓原理形成承載。

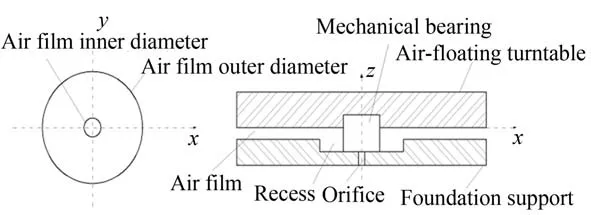
圖1 氣浮轉臺結構簡圖Fig.1 Structure diagram of air-floating turntable

2.2 氣膜流動控制方程

轉臺工作時氣膜厚度為微米級別，氣體流動為連續介質流動，所以遵循三個基本守恒定律：質量守恒定律（連續性方程）、動量守恒定律（N-S方程）和能量守恒方程（伯努利方程）。其中N-S方程可以描述流體流動的基本規律，但是其作為復雜的偏微分方程很難求解，因此基于一些假設建立連續性方程和簡化后的N-S 方程可以得到穩態氣膜潤滑Reynolds 方程：

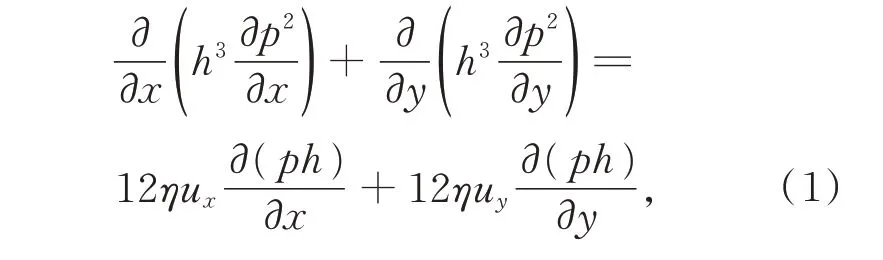
其中：p為氣膜壓力，η為氣體動力粘度，ux為轉臺在x方向的速度，uy為轉臺在y方向的速度。

在Reynolds 方程中，h為氣膜厚度，當轉臺存在角擺時：

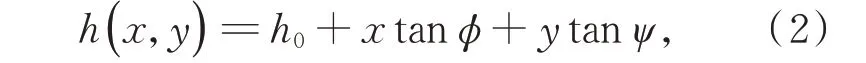
其中：h0為無角擺時氣膜厚度，?為繞y軸的角擺，ψ為繞x軸的角擺。

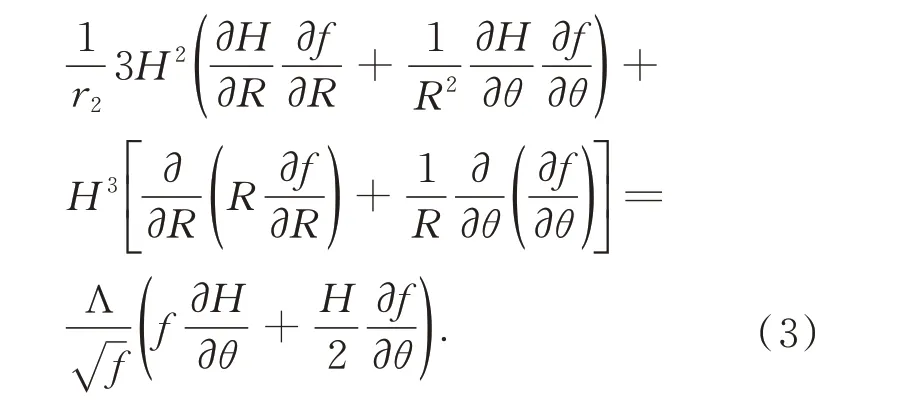
2.3 流量平衡方程

經過節流小孔的入口氣體流量為：

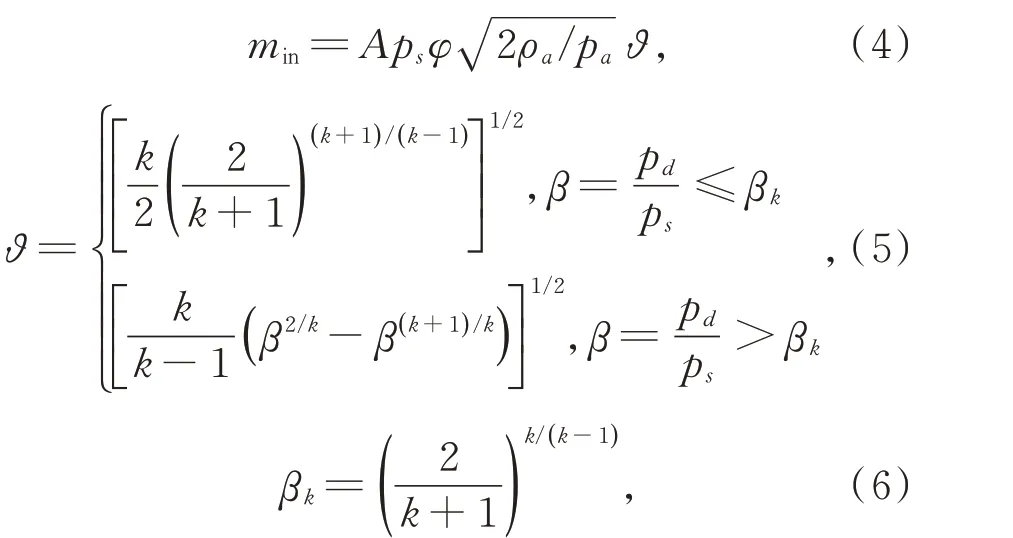
其中：A為小孔面積，ps為供氣壓力，φ為小孔流量系數，一般取0.8，ρa為大氣密度，pa為標椎大氣壓，?為流量函數，k為熱容比，一般取1.4，pd為均壓腔內氣體壓力，β為壓力比，βk為臨界壓力比。

出口流量滿足下列方程：

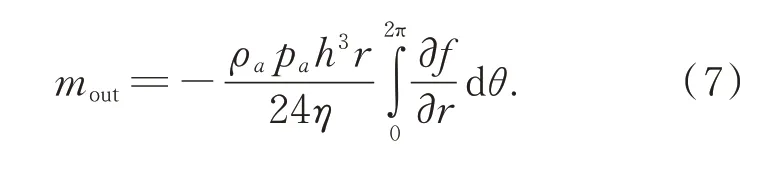
在穩態情況下，入口氣體流量應當等于出口氣體流量，則流量平衡方程為：

2.4 數值計算

雷諾方程是二階非線性偏微分方程，其解析解很難獲得，通常采用數值求解方法對其離散化得到可求解的代數方程組。常用的離散方法有FDM，FEM（有限單元法），FVM（有限體積法）以及DTM 等，FDM 在求解時計算用時少，編寫過程靈活，受到廣泛的應用。

如圖2 所示，將氣膜流場區域在周向和徑向分別劃分為n份和m份，則周向節點數為n，徑向節點數為m＋1。對于邊界條件：在與大氣相連處，fi，j=1。在均壓腔內，fi，j=(pd/pa)2。周期性邊界為fi＋n，j=fi，j。

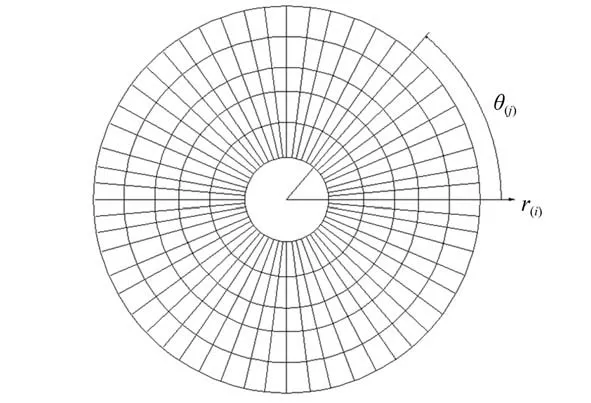
圖2 氣膜流場數值計算網格模型Fig.2 Numerical calculation grid model of air film flow field

采用五點中心差分將偏微分項進行轉化：

將（9）式帶入（3）式，則離散后的雷諾方程如下：

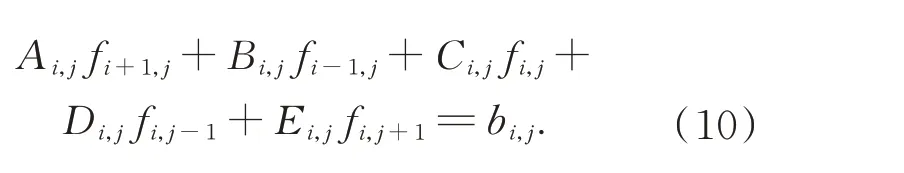
其中：

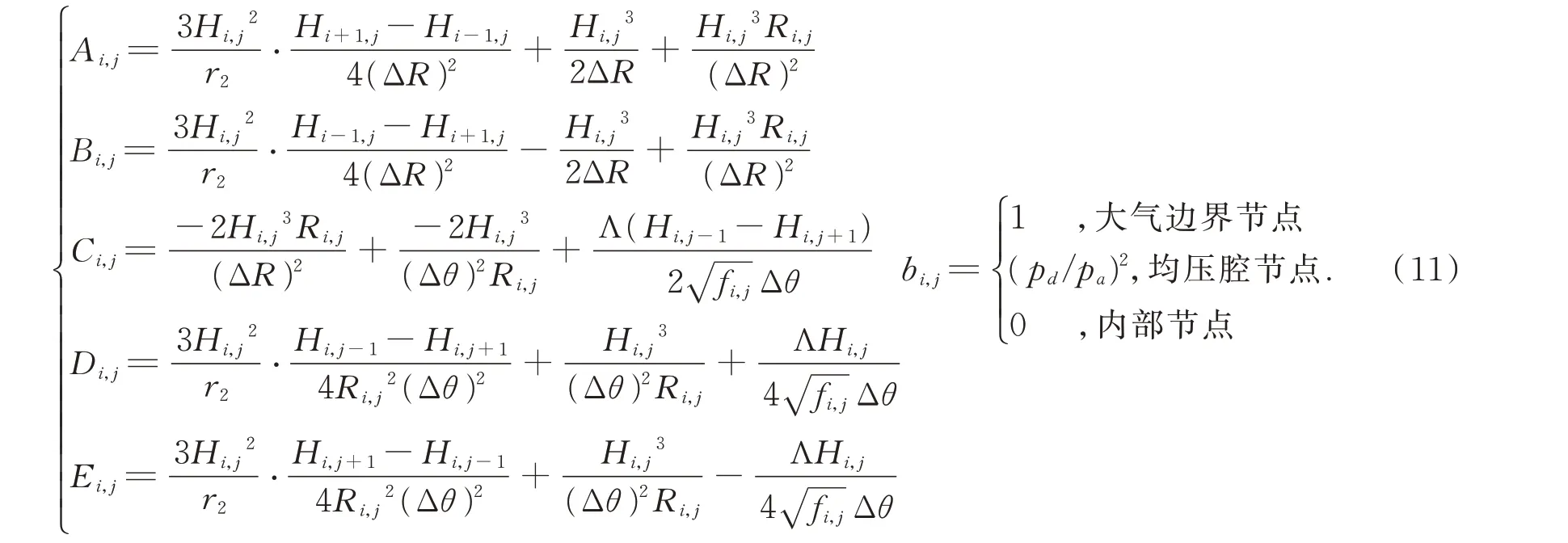
設定均壓腔初始壓力，結合流量平衡方程（8）便可求解離散后的雷諾方程（10），從而獲得氣膜厚度和壓力分布，具體流程如圖3 所示。將得到的壓力在整個氣膜面上進行積分，進而算出氣膜面的承載力：

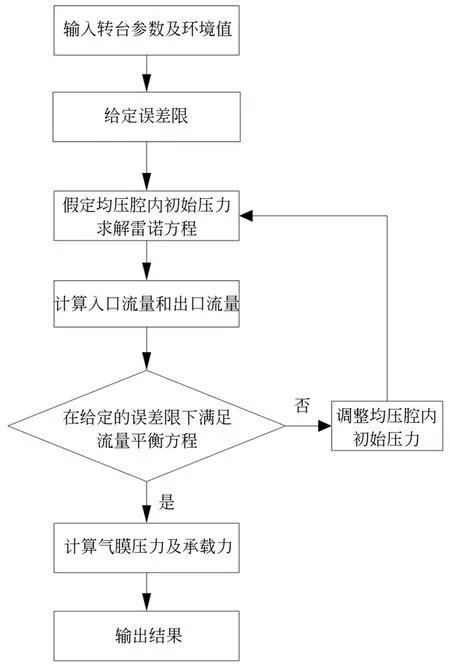
圖3 氣浮轉臺數值計算流程圖Fig.3 Flow chart of numerical calculation of air-floating turntable

3 算例結果及分析

如圖4 所示，將本文的計算結果和文獻［22］的結果進行對比，其計算參數見表1。由圖可知，兩者的壓力分布基本相似，從而驗證文中計算程序的正確性。

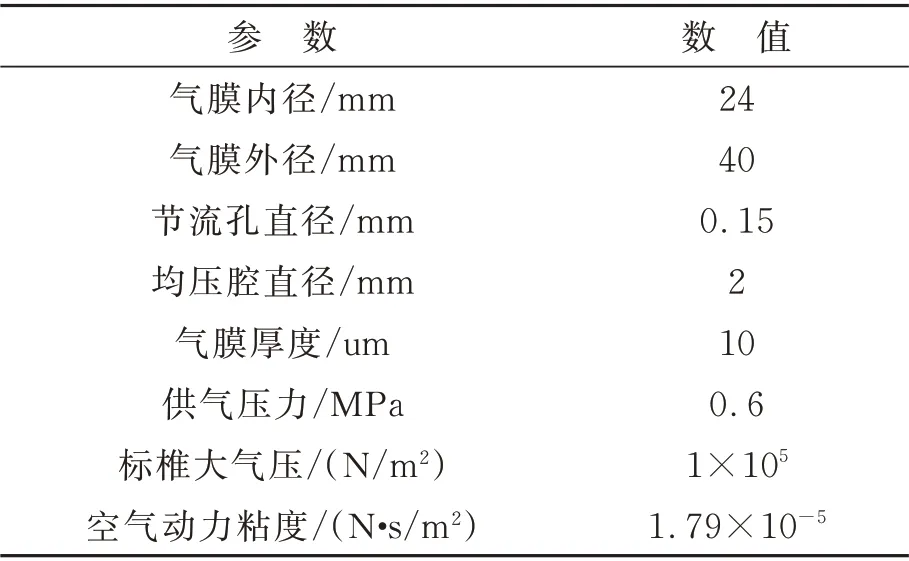
表1 文獻［20］計算參數Tab.1 Calculation parameters of reference［20］

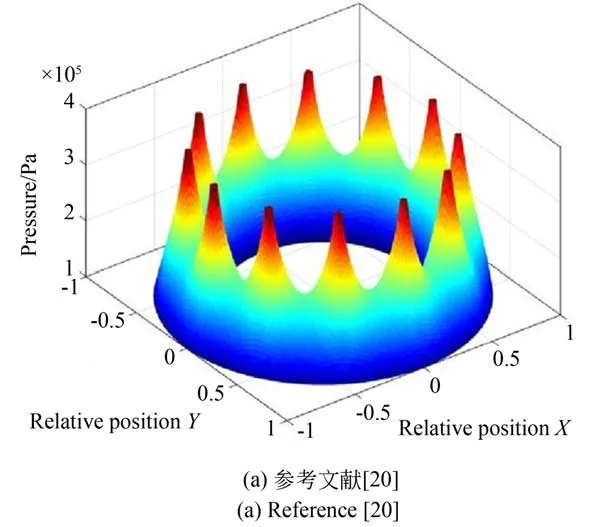
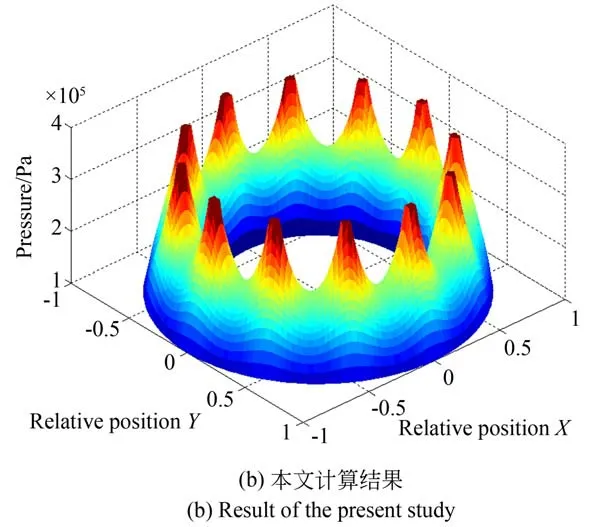
圖4 氣膜壓力分布Fig.4 Air film pressure distribution

表2 為本文的計算參數，使用其分析角擺和轉速對氣浮轉臺氣膜厚度、壓力分布等靜態特性的影響。

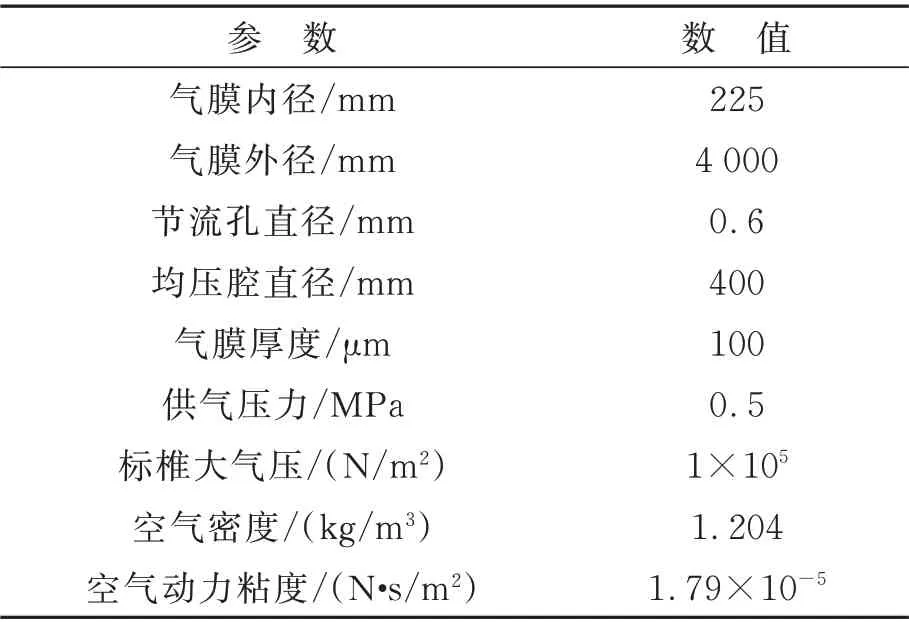
表2 本文計算參數Tab.2 Calculation parameters of the present study

3.1 單一角擺的影響

圖5（a）為不同角擺?下的氣膜厚度，由圖可知，隨著角擺的增大，氣膜厚度不再均勻分布。在x軸正方向（0～2 m），氣膜厚度逐漸增大；在x軸負方向（-2～0 m），氣膜厚度逐漸減小。這是由于氣浮轉臺存在角擺?時，氣膜厚度沿y軸發生了改變。將角擺繼續增大，圖5（b）為不同角擺?下的氣膜厚度最值。由圖可知，氣膜厚度最大值隨著角擺的增大逐漸增大，氣膜厚度最小值隨著角擺的增大逐漸減小。當角擺為0 rad 時，氣膜厚度最大值和最小值相同都為1，當角擺達到5×10－5rad 時氣膜厚度最大值為2 而最小值基本為0，這就意味著氣浮轉臺將與支撐體表面接觸，從而導致轉臺失效。這就說明轉臺角擺越大其失效的可能性越大，5×10－5rad 是本轉臺的最大極限角擺。

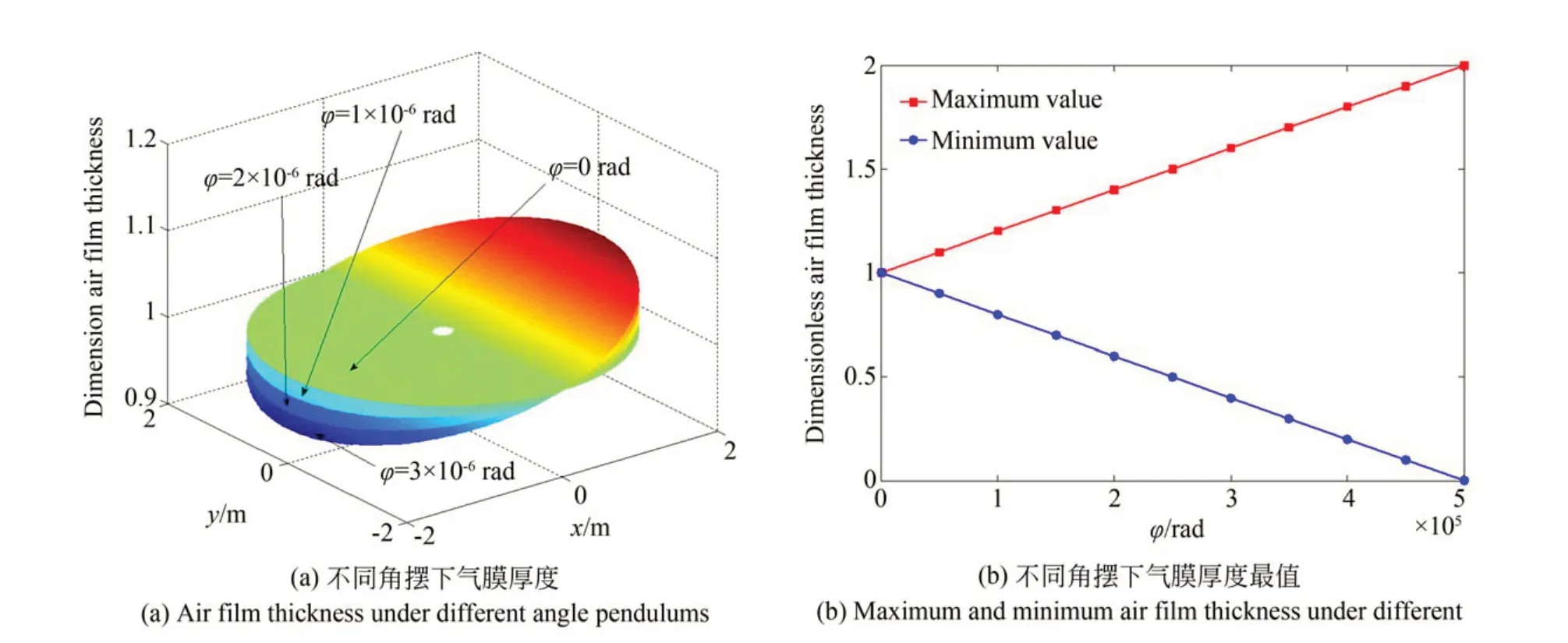
圖5 氣膜厚度Fig.5 Air film thickness

圖6 為不同角擺?下氣膜面的壓力分布圖，由圖可知，隨著角擺的增大，壓力不再對稱分布。在x軸負方向（-2～0 m），壓力隨角擺的增大而增大；在x軸正方向（0～2 m），壓力隨角擺的增大而減小，而在y軸方向上，壓力保持不變。這是由于在x軸方向上氣膜厚度發生改變，氣膜流場隨之變化，致使氣膜薄的區域壓力大，氣膜厚的區域壓力小，而在y軸方向上氣膜厚度未發生改變，因而產生這種現象。

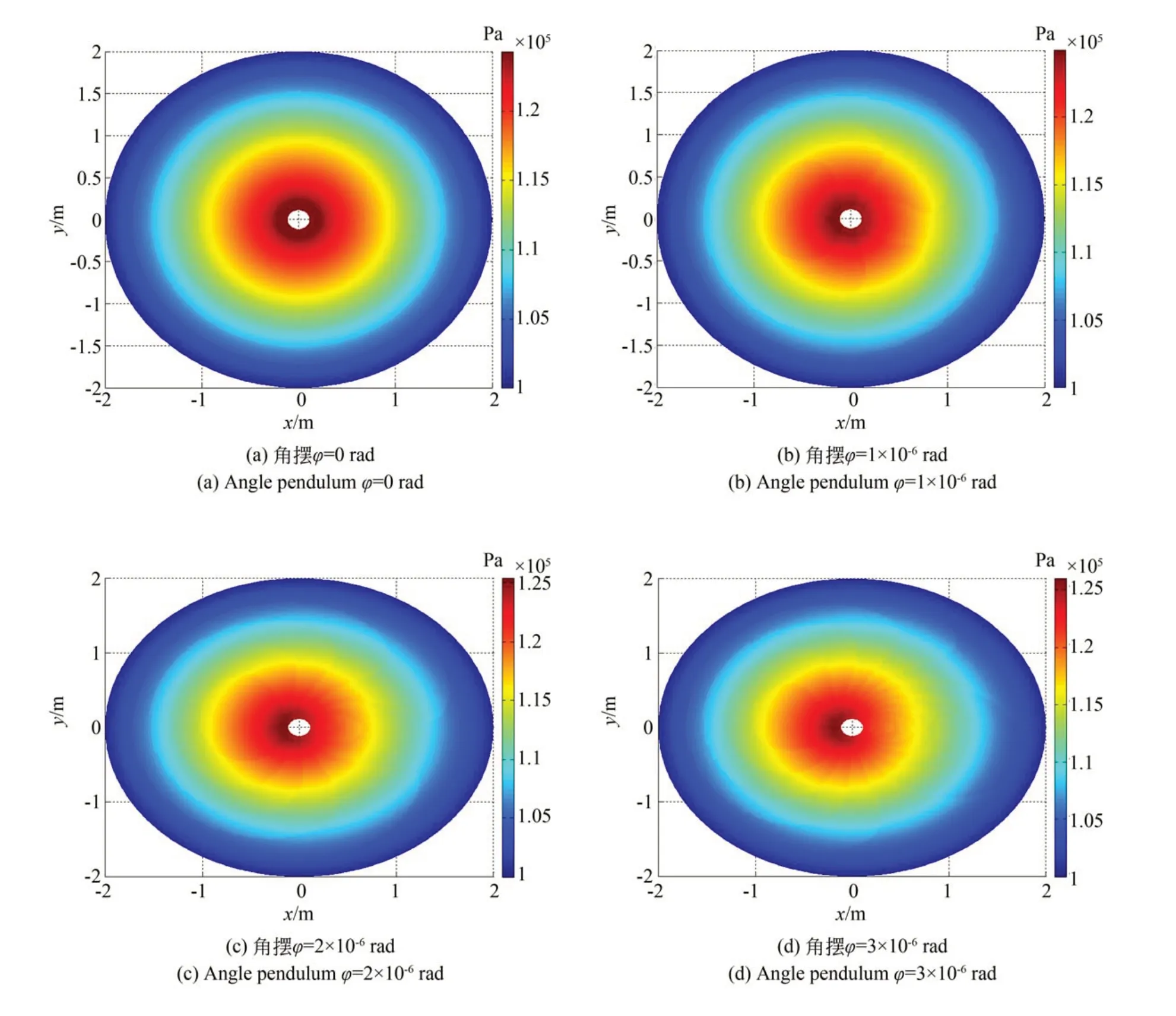
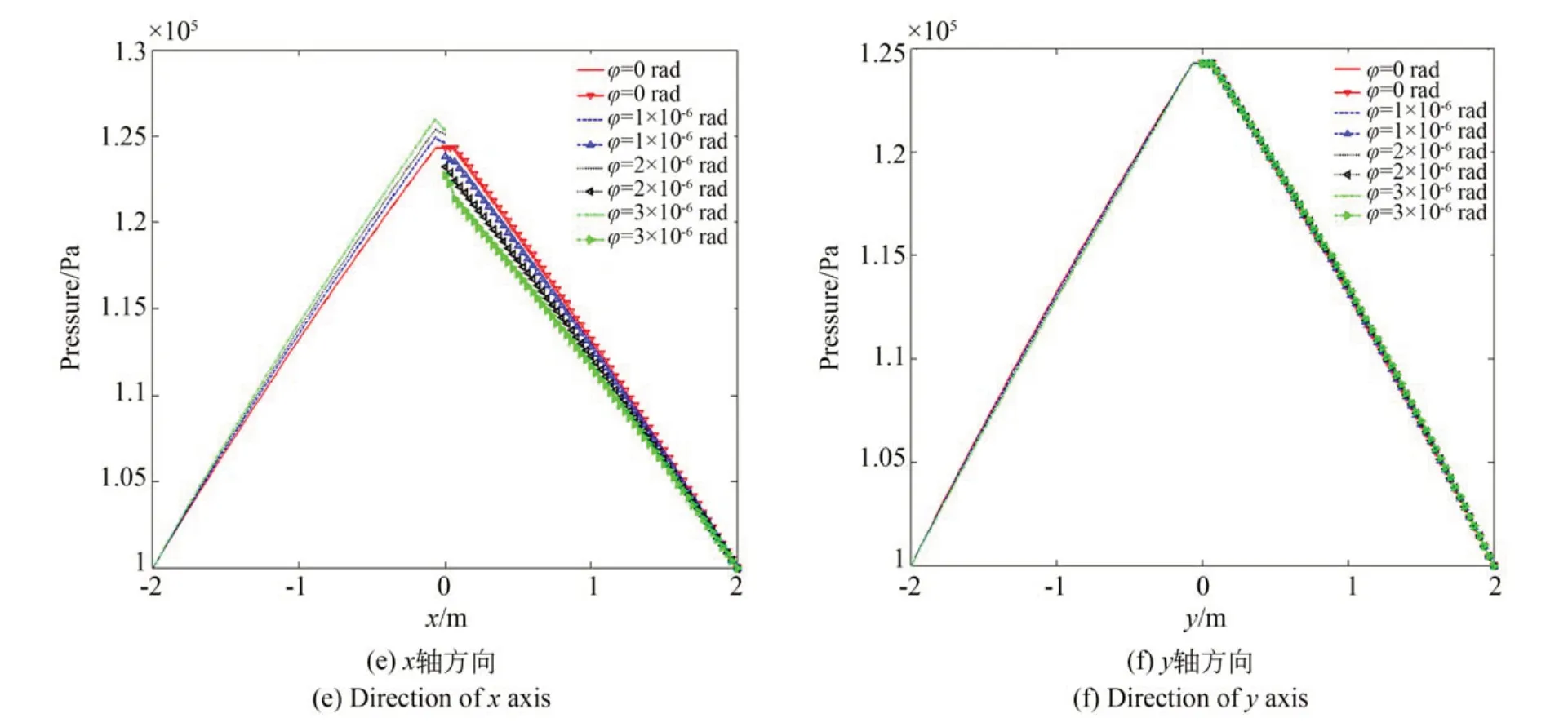
圖6 氣膜壓力分布Fig.6 Air film pressure distribution

由于角擺的變化致使氣膜厚度發生改變，從而導致整個氣膜面的壓力分布發生改變，而承載力為壓力在氣膜面上的積分，則氣膜承載力勢必發生改變。圖7 為不同角擺?下的氣膜承載力，由圖可知，隨著氣膜厚度的增大其承載力逐漸減小，這是由于氣膜壓力減小造成的。在同樣的氣膜厚度下，承載力隨著角擺的增大而減小。在供氣壓力一定的情況下，氣膜厚度是確定的，若是存在較大的角擺，則氣膜承載力下降。而為了保持力的平衡，則氣浮轉臺的位置會發生變化，從而導致超精密光學元件的表面形貌發生改變，影響加工精度。

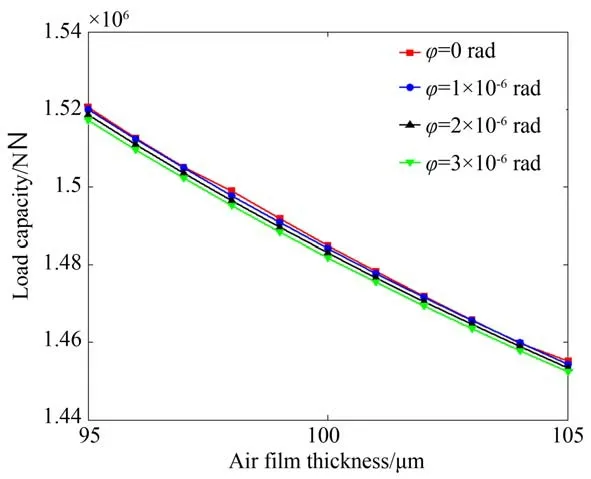
圖7 承載力Fig.7 Load capacity

3.2 組合角擺的影響

氣浮轉臺是軸對稱的，因而繞x軸的角擺ψ對轉臺靜態特性的影響和3.1 節是一致的。圖8為繞x軸的角擺ψ和繞y軸的角擺?同時存在時的氣膜厚度，圖中ψ取2×10－6rad，?逐漸增大。

由圖8（a）可看出，隨著角擺?的逐漸增大，在x 軸正方向（0～2 m）既存在氣膜逐漸變厚的區域，又存在氣膜逐漸變薄的區域，在其他方向也是如此，這一現象與存在單一角擺時有所不同。由圖8（b）可以看出，當角擺?達到4.9×10－5rad 時，氣膜厚度最小值基本為0，說明4.9×10－5rad 是轉臺的最大允許角擺。可知，相比于單一角擺時，組合角擺下轉臺的活動范圍更小。

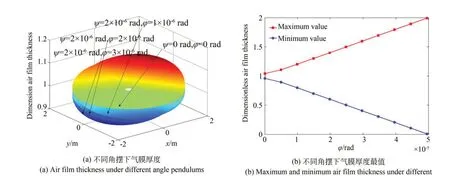
圖8 氣膜厚度Fig.8 Air film thickness

氣膜厚度的改變必然會引起壓力分布的變化從而最終導致氣膜承載力的改變。圖9 為不同角擺下氣膜承載力，對比單一角擺情形，可看出兩者規律基本一致。當角擺值從0 增大到3×10－6rad時（氣膜厚度為95，100和105 μm），單一角擺下承載力下降值分別為3.423 6×103 N，3.086 2×103和2.841 7×103 N，分別下降了0.23%，0.21%，0.20%。組合角擺下承載力下降值分別為4.309 9×103，3.823 2×103和3.437 5×103 N，分別下降了0.28%，0.26%，0.25%。表明組合角擺下承載力下降更加顯著，這是由兩種情形下氣膜厚度的改變不同所引起的。說明組合角擺下轉臺的位置改變更大，從而降低加工精度。

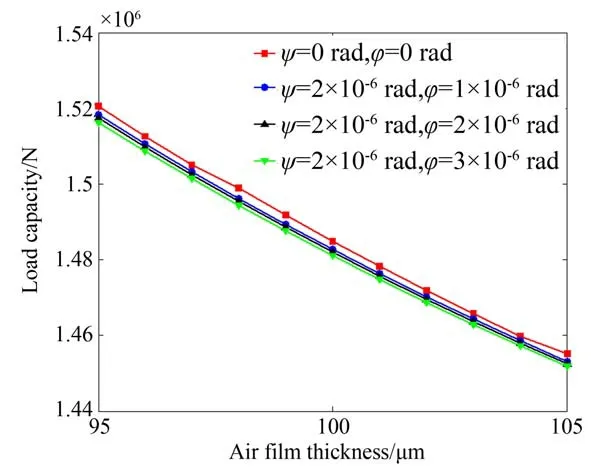
圖9 承載力Fig.9 Load capacity

3.3 轉速的影響

轉速實則為氣浮轉臺繞z軸的角擺，它是一個被利用的自由度。由式（2）知，轉速并不直接影響氣膜厚度，然而式（1）中含有轉速項，說明轉速不同會引起氣膜壓力的改變，這是由于轉速改變了氣膜內氣體的流速，導致氣膜內流場變化，從而引起壓力的改變。圖10 為不同轉速下氣膜面的壓力分布。由圖可知，隨著轉速的增大，高壓區域逐漸向外均勻擴散，然而壓力值卻逐漸減小。由圖10（e）知，當轉速達到2 300 r·min-1時氣膜中間均勻腔區域的壓力比周圍壓力小，此時流量平衡方程（8）也不再滿足，說明氣體潤滑已經失效，因而氣浮轉臺的轉速不能超過2 300 r·min-1。由于轉臺是軸對稱結構，且壓力是均勻擴散，所以圖10（f）和圖10（g）基本相同。

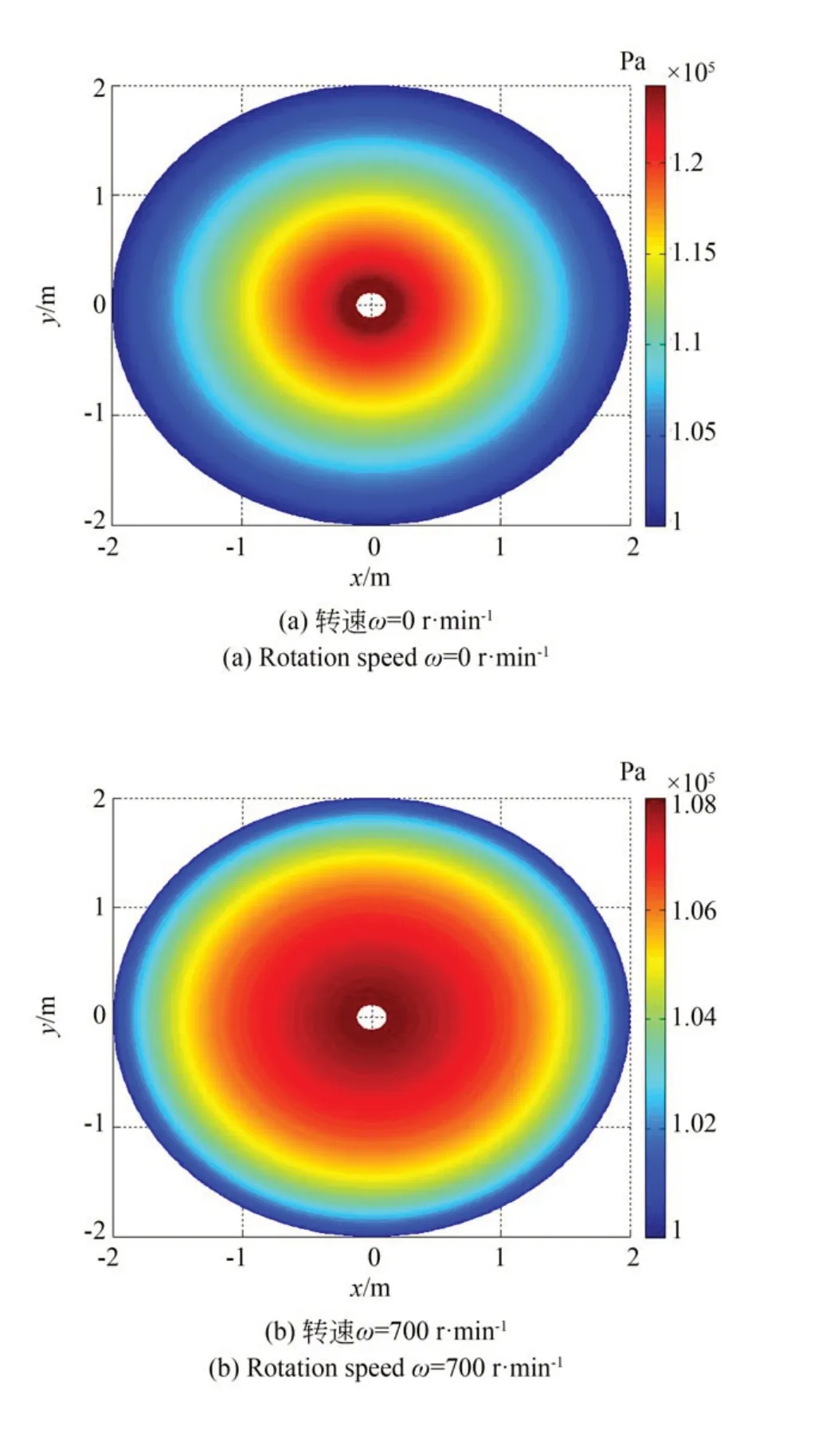
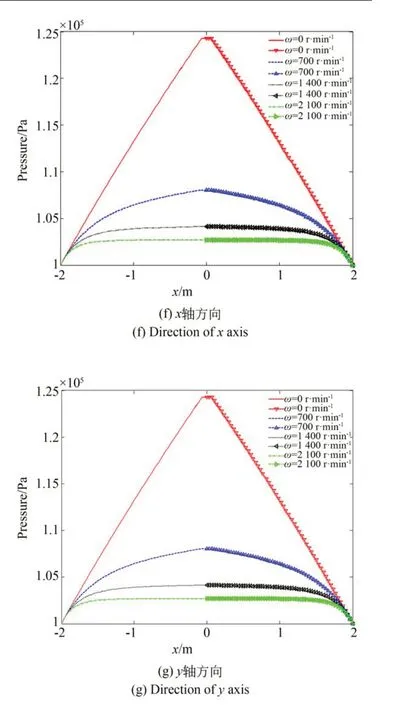
圖10 氣膜壓力分布Fig.10 Air film pressure distribution

圖11 為不同轉速下的氣膜承載力，由圖可知，隨著氣膜厚度的增加，承載力在逐漸降低，這與前面的分析一致。在相同氣膜厚度時，承載力隨轉速的增大而降低，當轉速從0 增大到2 100 r·min-1時（氣膜厚度為95，100 和105 μm），承載力下降值分別為2.038 0×105，1.750 2×105和1.496 1×105N，分 別 下 降 了13.40%，11.79%，10.28%，說明轉速的大幅度增大會引起承載力的快速下降。這可能是由于隨著轉速的提高，靜壓效應減弱，動壓效應增強，而此時減弱幅度大于增大幅度，因而承載力降低。

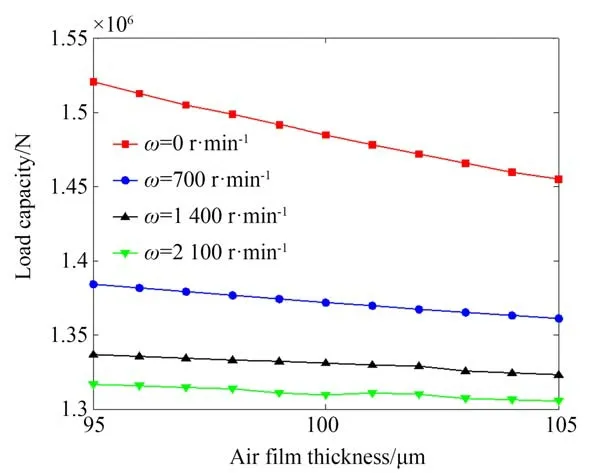
圖11 承載力Fig.11 Load capacity

在實際工作中增大轉速可以提高加工效率，然而轉速的增大會導致承載力的下降。參見表2，在供氣壓力為0.5 MPa 時氣膜厚度為100 μm。由圖11 知此時若將轉速從0 增大到2 100 r·min-1，則承載力由1.485×106N 減小到1.310×106N。工作時氣浮轉臺在空間中處于懸浮狀態。轉臺的質量一定，為了達到1.485×106N 的承載力，由圖12 知氣膜厚度會減小到47.5 μm，而此時轉臺的最大極限角擺為2.37×10－5rad，與之前的5×10－5rad 相比，其值大大減小。因而，將轉速增大2 100 r·min-1需將角擺減小2.63×10－5rad，應考慮減小或消除致使產生角擺的因素，比如降低偏載質量等。否則，會引起轉臺和支撐體表面接觸。此外，轉臺轉速也不能無限增大，當轉速超過2 300 r·min-1后，由于氣體潤滑失效，氣浮轉臺也會無法工作。

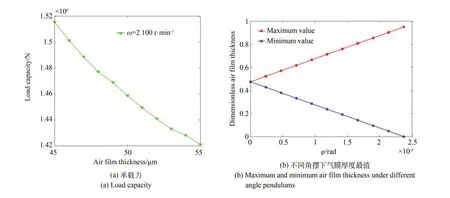
圖12 承載力和氣膜厚度最值Fig.12 Load capacity and maximum and minimum air film thickness

4 實驗測量

實驗測量氣浮轉臺角擺，采用激光位移傳感器，將傳感器吸附在大字形支架上，傳感器探頭對應拋光圓盤平面，圓盤靜止不動，安裝如圖13所示。氣浮轉臺在底部不供氣時，此時的坐標系設定為參考平面，即0 初始位置。測量時，供氣壓力為0.5 MPa，同時啟用三個傳感器測量，通過移動修正盤的位置可以改變拋光圓盤的傾角，一次測量得到三個位置高度信息。并對三個傳感器建立水平位置坐標系，結合高度信息建立三維空間坐標系。因為拋光圓盤為大理石材質，可以將其視為剛體，所以通過三個點可以建立一個圓形測量平面，其平面的傾角即為轉臺的角擺。通過計算可以得到圓盤最高位置以及最低位置點即氣膜厚度最大值和最小值，計算結果如表3所示。

圖13 氣膜厚度實驗測量平臺Fig.13 Experimental measurement platform of air film thickness

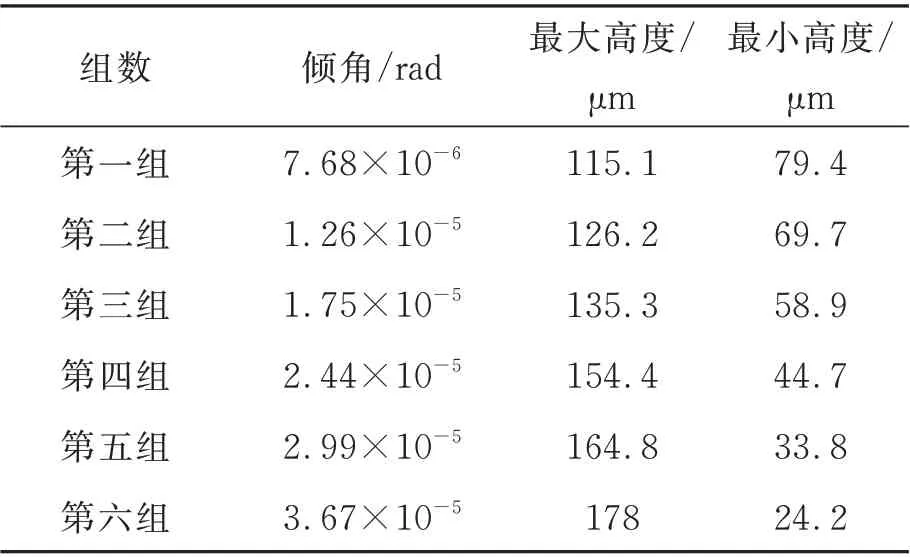
表3 實驗測量圓盤位置最值Tab.3 Highest and lowest value of the experimental measurement disc position

將實驗測量數據進行無量綱化處理，圖14 為實驗和理論對比圖，由圖可知兩者規律基本一致，最大誤差為14.4%。考慮到轉臺和測量平臺的制造及安裝誤差，可以認為理論數值計算和實際實驗是吻合的。

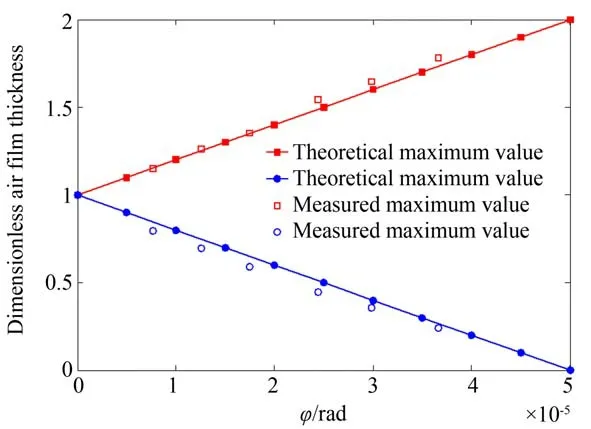
圖14 氣膜厚度最值的實驗和理論對比Fig.14 Experimental and theoretical comparison of the maximum and minimum air film thickness

5 結 論

本文根據超精密全口徑拋光機氣浮轉臺在實際工作時會存在傾斜角擺和一定轉速的特點，將考慮角擺后的氣膜厚度方程帶入雷諾方程，得到含角擺和轉速的雷諾方程。然后采用有限差分法將雷諾方程離散化處理，并結合流量平衡方程進行求解，通過和現有文獻結果的對比驗證程序的正確性。最后得到了單一角擺、組合角擺和不同轉速下氣膜厚度、壓力分布以及承載力這些靜態特性并通過實驗加以驗證。結果表明：隨著角擺的增大，氣膜厚度會發生改變，5×10－5rad是單一角擺下轉臺的最大極限角擺。氣膜厚度的改變影響壓力分布，最終導致承載力的下降；組合角擺下轉臺的最大極限角擺為4.9×10－5rad，組合角擺對轉臺靜態特性的影響更為顯著，但其影響規律和單一角擺時基本一致；隨著轉速的增大，氣膜壓力分布發生改變，承載力逐漸下降，當轉速超過2 300 r·min-1后，氣體潤滑失效，這就是轉臺的失效轉速。角擺和轉速的改變致使氣膜承載力發生變化，為了保持力的平衡，轉臺的位置也會隨之改變，從而影響超精密光學元件的加工精度。在實際工作中若將轉速增大2 100 r·min-1則應將最大極限角擺減小2.63×10－5rad，同時也要設法消除角擺以提高氣膜厚度的均勻性，從而降低承載力的波動以提高加工精度。該研究為后續雙向流固耦合研究氣浮轉臺的動態回轉誤差提供了理論基礎。