液壓滑閥內泄漏試驗研究

宋 飛，陳 佳，彭利坤，劉 杰

（海軍工程大學 動力工程學院，武漢 430033）

0 引言

液壓滑閥因其導向性好、體積小、功能多樣、噪聲低、易于加工制造等諸多優點在液壓傳動與控制系統中得到了廣泛應用。為了保證閥芯閥套間的良好密封和順暢滑動，正常滑閥閥芯和閥套間存在3～8 μm 的徑向間隙［1-2］，所以液壓滑閥內泄漏不可避免，但正常間隙時滑閥內泄漏量甚小，通常小于額定流量的0.1%［3-4］，對系統正常工作基本無影響。而當滑閥閥芯閥套磨損時，過大的徑向間隙會使內泄漏量顯著增加，嚴重時會影響執行機構正常動作，造成過多的壓力損失和系統異常發熱，甚至會導致滑閥機能失效。因此有必要對滑閥正常間隙和過大間隙下油液的流動狀態和泄漏規律進行研究，這對滑閥的設計及內泄漏量的預測都具有重要意義。

1 滑閥內泄漏模擬試驗臺工作原理

為研究液壓滑閥內泄漏規律，搭建完成了液壓滑閥內泄漏模擬實驗臺，該實驗臺主要由恒壓供油系統和滑閥內泄漏模擬裝置兩部分組成，供油系統用以提供壓力油，泄漏模擬裝置用以模擬滑閥內泄漏的真實狀況。

1.1 恒壓供油系統

恒壓供油系統原理如圖1 所示，該系統可為滑閥內泄漏模擬裝置提供0～10 MPa 的壓力油，與泄漏模擬裝置進出油口采用液壓軟管（長度≥5 m）相連，避免泵源及閥件振動噪聲對泄漏模擬裝置內泄漏狀態產生影響。供油管路上設置的蓄能器有兩個作用：（1）消除油源供油時產生的壓力脈動，以保持壓力穩定；（2）在液壓泵停止供油時作為輔助油源，實現在極安靜環境下為泄漏模擬裝置短時供油。回油管路上設置背壓加載閥，可通過節流作用控制泄漏模擬裝置的泄漏背壓。由于滑閥內泄漏量很小，故采用量筒+高精度流量傳感器的方式對其進行測量，兩者之間的切換通過電磁換向閥實現。

圖1 恒壓供油系統原理Fig.1 Schematic diagram of constant pressure oil supply system

1.2 滑閥內泄漏模擬裝置

滑閥內泄漏模擬裝置主要功能是模擬各工況下滑閥內泄漏的真實狀況，以研究各因素對滑閥內泄漏量的影響規律，裝置內部結構如圖2所示。

圖2 滑閥內泄漏模擬裝置Fig.2 Leakage simulation device of slide valves

該裝置可變參數有：閥芯直徑、間隙高度和密封長度，閥芯直徑和間隙高度的改變是通過更換閥體和閥芯的組合實現的，密封長度的改變是通過調節泄漏模擬裝置上的螺旋測微頭來實現的。設置有鎖緊機構，密封長度調整完畢后可通過鎖緊螺母將閥芯鎖緊，避免閥芯因液動力的作用位置發生改變。

2 環形縫隙泄漏量計算

假設液壓滑閥內泄漏處于層流狀態，且縫隙為同心環形縫隙，如圖3（a）所示，在無相對運動情況下同心環形縫隙層流泄漏量計算式［5-18］：

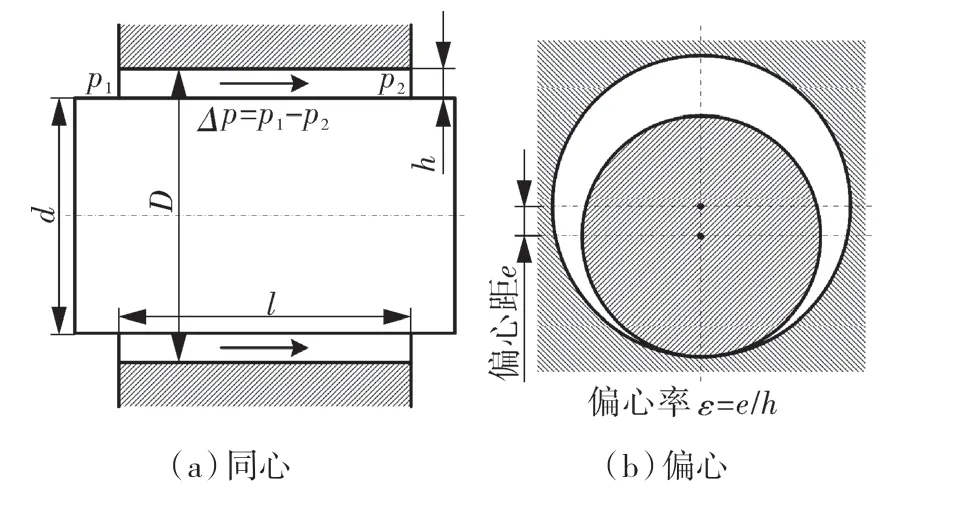
圖3 液壓滑閥環形縫隙Fig.3 Annular gap of hydraulic slide valves

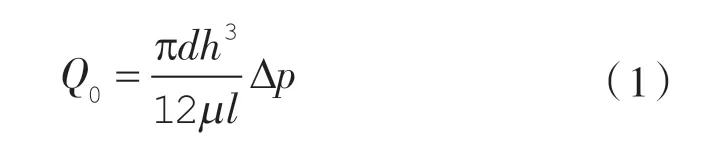
式中 d ——閥芯直徑，m；

h ——間隙高度，m，h=（D-d）/2；

D ——閥孔直徑，m；

μ ——油液動力黏度，Pa·s，μ=ρν；

ρ ——油液密度，kg/m3；

ν ——油液運動黏度，m2/s。

l ——密封長度，m；

Δp ——上、下游壓差，Pa。

閥芯和閥套平行，但存在偏心時，如圖3（b）所示，泄漏量的計算式：

若處于層流狀態，綜合考慮偏心和傾斜的影響，由式（2）～（4）可知，實際層流下的泄漏量應為：

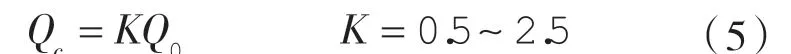
若處于紊流狀態，在無相對運動情況下同心環形縫隙紊流泄漏量計算式［9-11］：

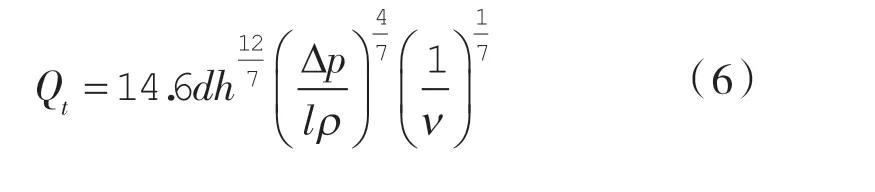
依據雷諾數判斷流體的流動狀態究竟是層流還是紊流，雷諾數計算式：

式中 v ——油液流速，m/s；

dh——水力直徑，m。

由于為同心環形縫隙流道，可知：

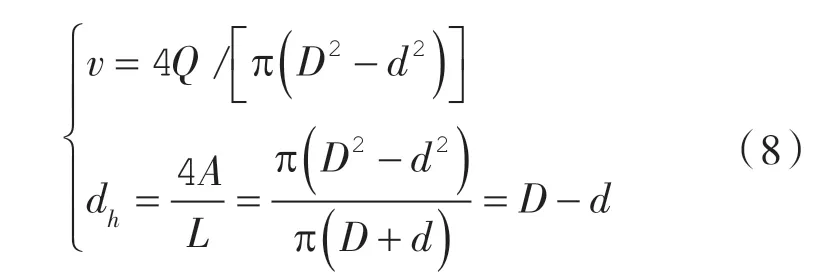
式中 Q ——縫隙泄漏量，m3/s；

A ——過流面積，m2；

L ——濕周，m。

將式（8）和 μ=ρν代入式（7），可得：

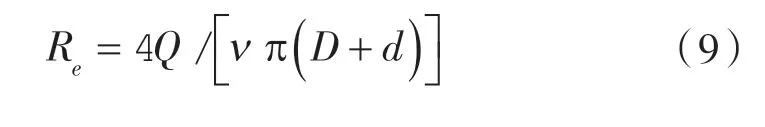
3 試驗結果分析

利用液壓滑閥內泄漏模擬實驗臺對閥芯直徑分別為10，16，20 mm 的液壓滑閥在正常間隙（5 μm）和過大間隙（40 μm）下的泄漏規律進行了試驗研究，試驗中選取的可變參數為密封長度（0.25，0.50，1.00，1.50，2.00 mm）和 壓 差（2，4，6，8，10 MPa）。試驗采用46#抗磨液壓油，油液密度 ρ=850 kg/m3，運動黏度ν=4.5×10-5m2/s，為減小油液溫度對試驗的影響，系統啟動后待達到熱平衡狀態后再開始試驗。

3.1 正常間隙時的泄漏

在正常間隙下，通過試驗得到液壓滑閥在各密封長度和壓差下的內泄漏量，密封長度對泄漏量的影響如圖4 中實線所示，壓差對泄漏量的影響如圖5 中實線所示。

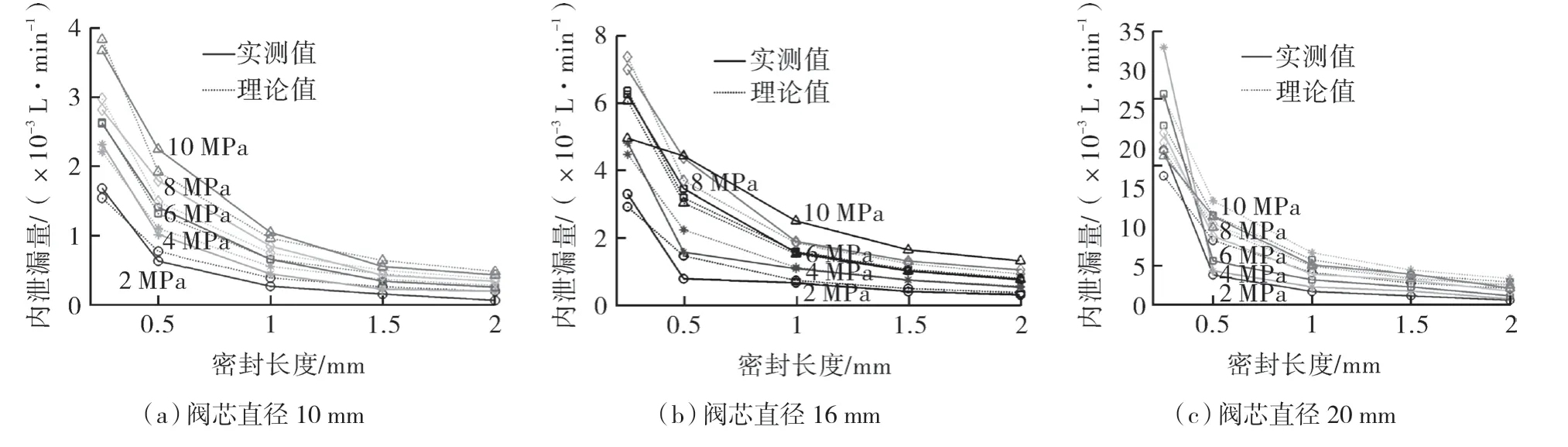
圖4 正常間隙時密封長度-泄漏量曲線Fig.4 Sealing length-leakage flow curve at normal clearance

圖5 正常間隙時壓差-泄漏量曲線Fig.5 Pressure difference-leakage flow curve at normal clearance

相關文獻表明對于液壓系統而言，由于油液黏度大，而且間隙極小的縫隙流動中黏附力起主要作用，故縫隙流通常處于層流流動狀態［6-8，10，14］。由圖4 可知滑閥內泄漏量與密封長度基本成反比關系，由圖5 可知，除個別差異較大的點之外，泄漏量與壓差基本成正比關系，這些規律與式（1）是一致，也能說明滑閥內泄漏應處于層流流動狀態。

利用式（9）計算得到各閥芯直徑縫隙流的雷諾數見表1。用式（1）（6）計算得到同心環形縫隙的層流泄漏量Q0和紊流泄漏量Qt，將其與實測泄漏量Q 進行對比，具體數值見表1。

由表1 可知，正常間隙時各閥芯直徑下的內泄漏雷諾數遠小于同心環形縫隙臨界雷諾數1 100，而且也小于閥口臨界雷諾數260［16-17］，可見泄漏是處于層流流動狀態的。通過泄漏量的對比可知，實測泄漏量遠小于紊流泄漏量，與層流泄漏量接近，且除個別較大比值點外，基本都在0.5～2.5 范圍內，與式一致，說明正常間隙下泄漏確實是處于層流流動狀態的。從對比中也能看出，由于泄漏模擬裝置兩端沒有很好的固定對中，閥芯在閥套內的確存在偏心和傾斜的情況；而且閥芯閥體配合間隙很小，加工過程中存在尺寸和形位公差都會造成微觀流道的改變，如：表面粗糙度、錐度等；此外試驗中由于試驗條件所限，也并未對油液溫度進行主動精確控制，溫度平衡點會隨著工作壓力的升高而升高，油液黏度可能會在較大范圍波動，這些因素都是導致比值在較大范圍內分布的原因。

通過上述分析，充分說明正常間隙下滑閥內泄漏是處于層流流動狀態的。由于閥芯實際的偏心和傾斜情況無法測定，即式（5）中K 的大小無法確定，這里利用實測點對式（5）進行最小二乘擬合間接得到K 的大小，據此得到的理論泄漏量曲線如圖4，5 中虛線所示。

由圖4 可知，實測與理論泄漏量曲線非常接近，密封長度與內泄漏量基本成反比關系，閥芯直徑越大，壓差越大，密封長度越小，內泄漏量越大，上述結論與公式相符。此外，當密封長度≥1.0 mm 時，滑閥內泄漏量變化趨于平緩，這意味著當密封長度增加到一定程度時，采取繼續增加密封長度減小泄漏量的方法將收效甚微，而且還會導致滑閥死區的增大。

由圖5 可知，除密封長度0.25 mm 的曲線外，其他密封長度下壓差和泄漏量基本成正比，隨著壓差的增加，泄漏量線性增加，上述結論與公式相符。密封長度0.25 mm 的泄漏量隨壓差的增加呈現先增大后減小的趨勢，這可能是由于隨著壓力的升高，閥芯受力情況發生了變化，其在閥套內偏心和傾斜的程度發生改變，進而導致了泄漏量的下降。

3.2 間隙過大時的泄漏

液壓滑閥在使用過程中由于閥芯和閥套的磨損會使其徑向間隙變大，由式和式可知內泄漏量至少與徑向間隙二次方是成正比的，所以內泄漏量會隨著徑向間隙增大快速增加，過大的內泄漏量會嚴重影響系統的正常工作。為研究過大間隙下的滑閥內泄漏規律，利用液壓滑閥內泄漏實驗臺在徑向間隙40 μm 的條件下進行泄漏試驗。滑閥正常磨損導致的間隙增大通常不會超過40 μm，選取40 μm 徑向間隙基本可以覆蓋最極端的泄漏情況。通過試驗同樣得到液壓滑閥在各密封長度（密封長度0.25 mm 除外）和壓差下的內泄漏量，密封長度對泄漏量的影響如圖6 中實線所示，壓差對泄漏量的影響如圖7 中實線所示。

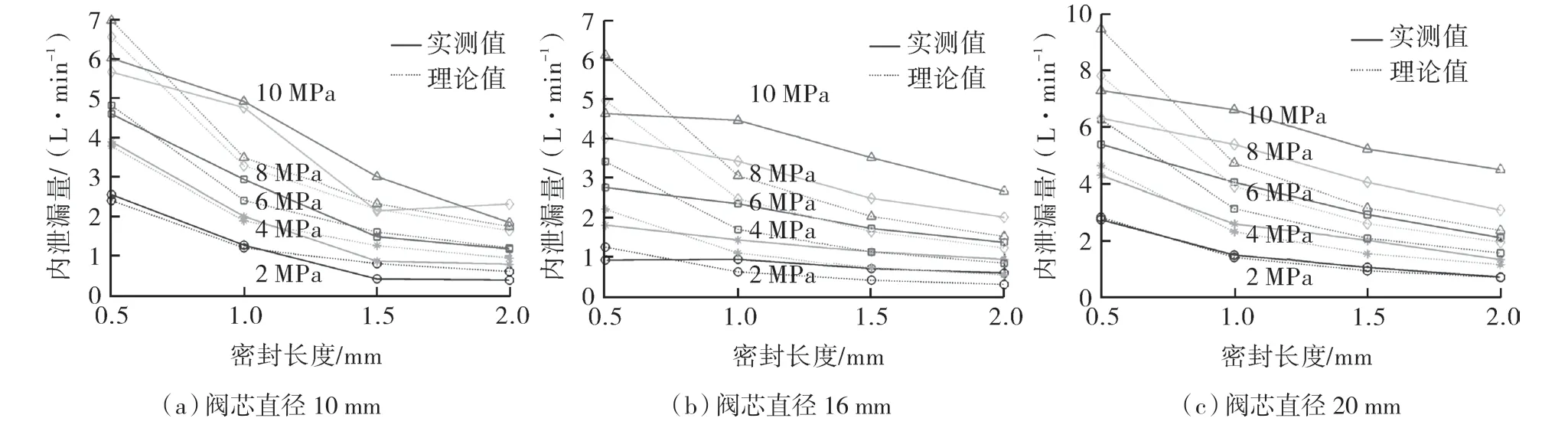
圖6 間隙過大時密封長度-泄漏量曲線Fig.6 Sealing length-leakage flow curve at excessive clearance

圖7 間隙過大時壓差-泄漏量曲線Fig.7 Pressure difference-leakage flow curve at excessive clearance

計算得到各閥芯直徑縫隙流的雷諾數、層流泄漏量Q0與實測泄漏量Q 的比值、紊流泄漏量Qt與實測泄漏量Q 的比值見表2。

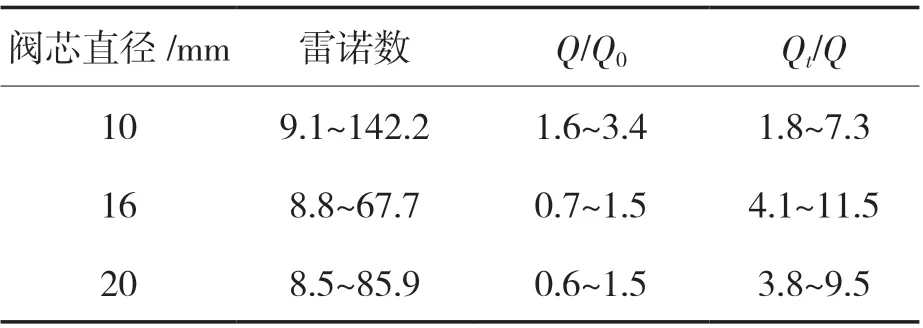
表2 過大間隙下層紊流分析Tab.2 Laminar turbulent flow analysis under excessive clearancee

由表2 可知，過大間隙時各閥芯直徑下的內泄漏雷諾數雖然比正常間隙時大很多，但也遠小于同心環形縫隙臨界雷諾數1 100，也尚未達到閥口臨界雷諾數260［19-20］，若以雷諾數作為判斷依據，過大間隙時的泄漏仍是層流流動。通過泄漏量的對比可知，實測泄漏量與層流泄漏量和紊流泄漏量都較為接近，但更接近層流泄漏量，除個別較大比值點外，其余基本都在0.5～2.5 范圍內，與式（5）一致，說明過大間隙下的泄漏是處于層流流動狀態。閥芯在閥套內也存在偏心和傾斜的情況，但與正常間隙相比其比值分布范圍更為集中，這可能是由于過大間隙下的泄漏量較大，試驗中的干擾因素和測量誤差對其影響有限。

通過上述分析，說明過大間隙下滑閥內泄漏也是處于層流流動狀態的，利用實測點對式（5）進行最小二乘擬合間接得到K 的大小，據此得到的理論泄漏量曲線如圖6，7 中虛線所示。

通過圖4，6 的對比可知，過大間隙下的泄漏量遠大于正常間隙下的泄漏量，這也印證了徑向間隙是影響泄漏量的最關鍵因素，若要減少泄漏減小徑向間隙將是最為直接的方法。圖6 中實測和理論泄漏量曲線在壓差較小時較為接近，壓差較大時，實測與理論泄漏量曲線差異較大。密封長度與內泄漏量的反比關系并不明顯，特別是密封長度0.5 mm 處的泄漏曲線存在實測值普遍小于理論值的情況。根據式（1）可知，當密封長度l →0 時，泄漏量Q0→∞，這顯然與實際情況是不符的，也能解釋為什么在小密封長度下會出現泄漏量實測值小于理論值的情況。

由圖7 可知，各密封長度下實測與理論泄漏量曲線吻合較好，壓差和泄漏量基本成正比，該結論與式（1）相符。密封長度0.5 mm 下的實測與理論泄漏量曲線偏差稍大，且實測泄漏量曲線斜率呈現不斷減小的趨勢，造成這種現象的原因一方面可能與閥芯在閥套內偏心和傾斜的程度發生改變有關，另一方面可能是由于該密封長度下泄漏已開始向紊流狀態過渡，式（6）中壓差Δp 的指數小于1，意味著泄漏量曲線的斜率是隨著壓差的增加不斷減小的，這與實測泄漏量曲線是相符的。

4 結論

（1）正常間隙和過大間隙下液壓滑閥的內泄漏均處于層流流動狀態，可利用層流公式進行內泄漏量的計算和預測。

（2）實測泄漏量與理論泄漏量通常都會存在一定的差異，偏心、傾斜和溫度等因素都會對泄漏量產生影響，計算或預測應給予考慮，具體參考式（5）。

（3）當密封長度≥1.0mm 時，滑閥內泄漏量變化趨于平緩，繼續增加密封長度減小泄漏量的作用有限。

（4）對于層流公式，當密封長度l →0 時，泄漏量Q0→∞，這顯然與事實不符，在小密封長度下進行泄漏量計算或預測會出現較大偏差。

（5）無論是層流或是紊流，泄漏量對徑向間隙高度的變化最為敏感，減小徑向間隙是減少泄漏量最為直接的方法。