基于L曲線調參的FOTV-ADMM超分辨率圖像重建*
徐 文,楊曉梅,徐秋怡,田巧玉,劉 凱
(1.四川大學錦江學院 電氣與電子信息工程學院,四川 眉山 620860; 2.四川大學 電氣工程學院,成都610207;3.中央民族大學 信息工程學院,北京100081)
0 引 言
大數據信息時代,超分辨率圖像重建技術通過軟件編程的方式來提高圖像的分辨率,在沒有替換原有的成像設備前提下,從包含不同細節的低分辨圖像中采集有用信息融合成一幅高分辨圖像。其技術主要的思想是用同一場景的圖像序列的時間分辨率來換取更高的一個空間分辨率[1]。通過超分辨重建的方法處理視頻圖像就是從多個低分辨率圖像中連續幀之間的相關聯系來得到原始圖像中高分辨圖像的相關信息,獲得更清晰、分辨率更高、內容信息更加豐富的圖像視頻信息。超分辨率圖像和視頻重建在監控設備、衛星圖像和醫學影像等領域都有重要的應用價值。
20世紀80年代,Tsai和 Huang[2]首先發現了基于序列或多幀圖像的超分辨率重建問題,他們通過實驗分析且證明了從互相平移得到的圖像序列中能夠獲取到分辨率更高的靜態圖像,并且給出了在從時域轉換到頻域里解決問題的方法。近年來,壓縮感知增強技術和超分辨率圖像復原技術為圖像復原的研究注入了新的力量[3-9]。人工智能中深度學習的發展,突破了圖像的分割和分類的傳統技術,特別是基于卷積神經網絡(Convolutional Neural Network,CNN)的單幅圖像重建(Super-Resolution CNN,SRCNN)[10]算法能夠快速重建高分辨率的圖像。但SRCNN算法對網絡參數敏感,要求訓練參數稠密,減緩了訓練速度,對細節恢復效果欠佳。VDSR(Accurate Image Super-Resolution Using Very Deep Convolutional Networks)[11]算法提出只針對殘差進行訓練,減輕了網絡的負擔,又加速了學習速率。再之后的SRGAN(Super-Resolution GAN)[12]等算法將生成式對抗網絡(Generative Adversarial Network,GAN)用于SR問題,提升重建圖片的真實感。
從數學角度看,超分辨率重建是一個典型的病態不適應問題[13]。 對于不適應問題,正則化的求解方法是非常有效的。正則化的方法為保證求解過程的穩定性,通過加入性質不同的先驗信息來約束重建過程,從而將超分辨率圖像重建由病態轉為良態問題。相對于深度學習圖像處理問題,基于三層神經網絡SRCNN算法雖然通過使用較大的卷積核可以減少計算量,但卷積計算時大量丟失高頻信息,對于紋理的處理仍然出現過平滑,特征的提取不夠準確,重建質量受到影響。SRGAN算法能提升高頻圖像真實感,但仍存在放大細節部分的像素塊模糊[12]。 考慮到此類模型訓練的數據量龐大與研究設備費用高昂問題,本文仍堅持以傳統非深度學習的方法為研究重點,探討正則項的選取對于圖像高頻紋理細節重建保持問題,分析超分辨率圖像重建的過平滑現象根源,改善圖像重建質量。
2 超分辨率圖像重建方法
本文提出基于傳統的全變分正則化(Total Variation,TV)模型引入了交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[14]。 ADMM重建算法將有約束的問題轉化為無約束的問題,在求解模型中某一個變量的同時固定另一個變量,通過固定迭代的方式更新模型中的每一個變量達到求解目的。針對TV-ADMM重建效果中出現的問題,本文引入分數階全變分(Fractional Order Total Variation,FOTV)正則項約束的模型,同樣使用ADMM算法進行求解,改善超分辨率圖像重建效果。
2.1 ADMM算法
ADMM算法是專門用于解決可分離凸規劃問題而被提出的一種方法,適用于各類優化問題。ADMM算法一般解決的問題形式如下[14]:
minf(x)+g(z)
(1)
s.t.A(x)+B(z)=C。
(2)
式中:x∈n,z∈m,A∈p×n,B∈p×m,C∈p,p、m、n分別為空間的維度;f(x)和g(z)表示的是凸函數;增廣拉格朗日(Lagrangian)函數用于求解凸優化問題,
Lρ(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-C)+
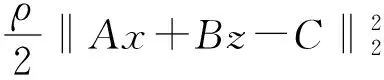
(3)
式中:λ為Lagrangian 乘子,ρ>0為懲罰參數。
ADMM算法的迭代步驟如下:
xk+1=arg minxLρ(x,zk,λk) ,
(4)
zk+1=arg minzLρ(xk+1,z,λk),
(5)
λk+1=λk+ρ(Axk+1+Bzk+1-C) 。
(6)
式中:ρ>0是懲罰參數。ADMM迭代算法包括x、z變量極小化和一個對偶變量的迭代。為方便計算,將ADMM算法迭代步驟等價為下列式子,定義參量
r=Ax+Bz-C,
(7)
計算得到
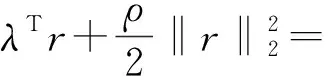
(8)
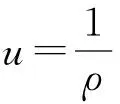
(9)
(10)
uk+1=uk-Axk+1+Bzk+1-C。
(11)
乘子法和ADMM乘子法類似,把x、z兩個變量一起求解,而ADMM是將目標函數分離求解,和Gauss-Seidel方法迭代一步類似。和乘子法相似,只是用zk+1最小化式子:
(12)
其中用到了對偶式子
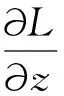
(13)
ADMM算法的有效性主要由選取的拉格朗日(Lagrange)乘子決定,可以從算法的收斂性分析中得出。
2.2 基于TV-ADMM的超分辨率圖像重建
超分辨率圖像退化模型表示為[15]
Y=DHMu+n。
(14)
式中:u為高清圖像,Y為低分辨率圖像,D為下采樣因子,H為模糊因子,M為運動因子,n為隨機噪聲,μ為正則化參數,本文中沒有移位變換所以M不考慮為1。基于TV全變分約束的正則化圖像重建模型描述為以下形式:
(15)
模型由保真項和正則項組成,其中正則項φ(u)=TV(u)為全變分[16]可以表示為圖像像素離散梯度之和,即離散梯度的l1范數形式:
(16)

(17)
(18)
超分辨率圖像重建問題(15)是病態的逆問題,ADMM算法通過引入變量d替換原模型中的不可微項φ(u),可以得到與其等價的約束優化問題:
(19)
對于約束優化問題,其增廣拉格朗日乘子函數
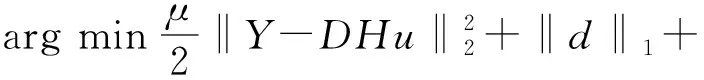
(20)
式中:<>表示內積。從而將式(20)轉換為兩個子問題m、n。
(1)子問題m:固定u求d
(21)
子問題m可以通過收縮閾值方法求解:
(22)
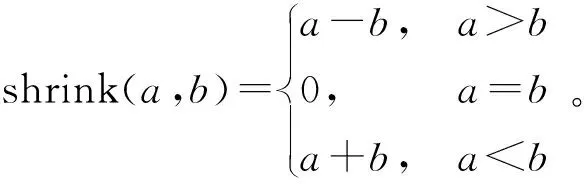
(23)
(2)子問題n:固定d求u

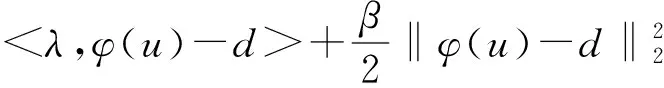
(24)
問題(24)等價于
(25)
本文中φ(u)=u為正則項,其中Y是輸入的低分辨圖像。用快速傅里葉變換處理公式(25),得
μHTDT(DHu-T)+λT+βTu-βTd=0,
(26)
(27)
更新
λk+1=λ-γβ(dk+1-u) ,
(28)
Yk+1=Yk+(Y-DHuk+1) 。
(29)
2.3 基于L曲線調參的FOTV-ADMM圖像重建
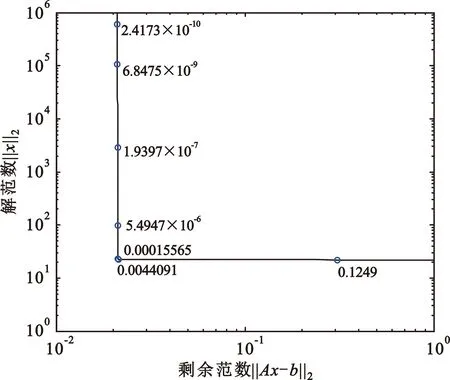
L曲線是以(‖Axμ-b‖2,‖xμ‖2)為坐標所構成的一條單調遞減曲線,該項對應于本文模型(15)中的‖Y-DHu‖,這些點與正則化參數呈一一對應的關系。圖1為Tikhonov正則化的L曲線[17],其中圓圈表示TGSVD正則化的L曲線。
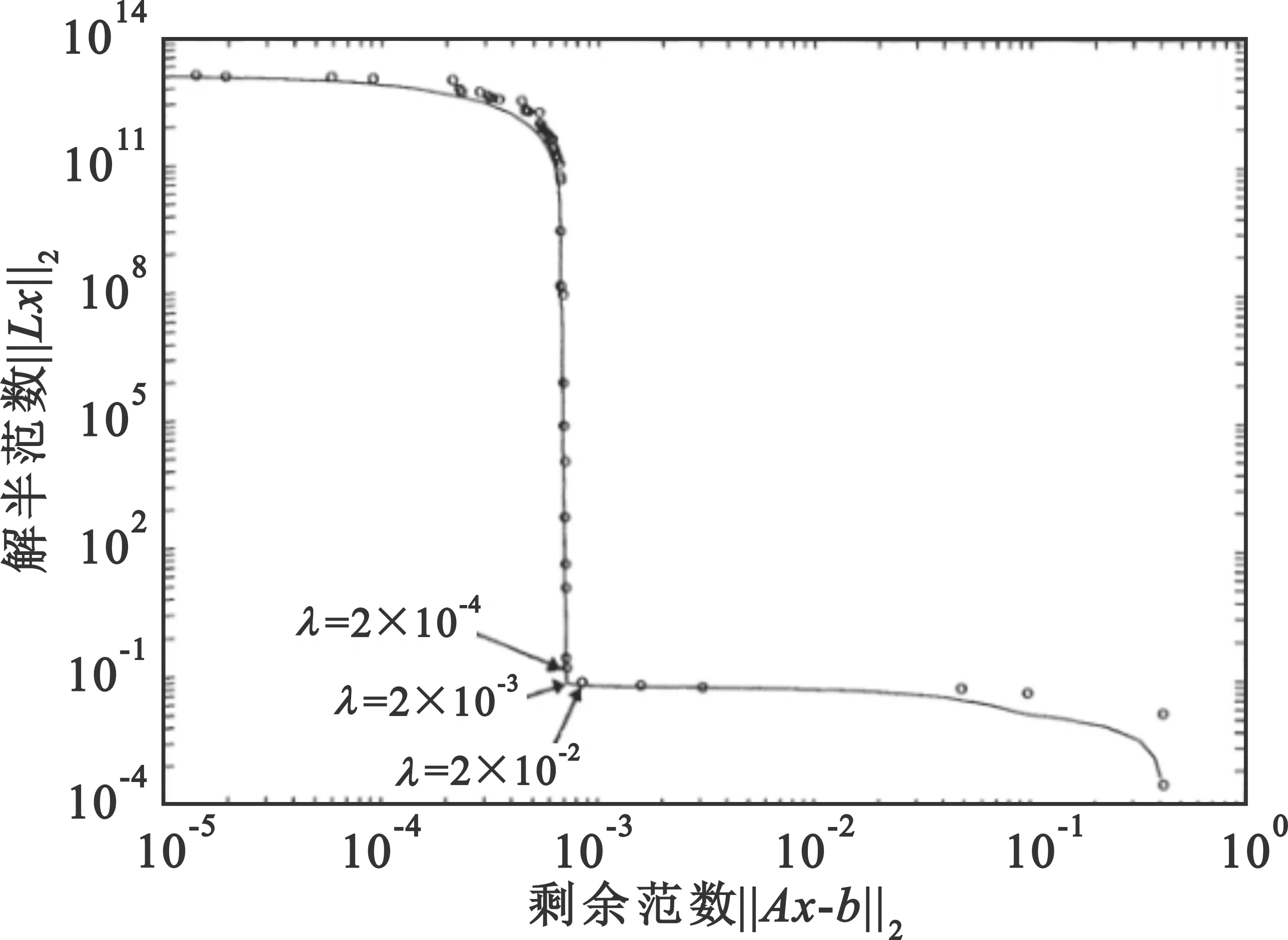
圖1 Tikhonov正則化的L曲線
‖Axμ-b‖2為殘差項,‖Lxμ‖2為正則化解,對于L曲線法來說,作為基本問題需要同時考慮到正則化解和殘差項。圖1中L曲線水平部分與垂直部分的相交處作為正則化最優參數解。由于正則化參數過大會引起正則化誤差主導水平位置對應的正則化解,過小則會使垂直部分對應的正則化解主要受到b中的誤差影響,而在相交處,均衡了都較小的一個,因此這個相交點就對應了一個最優的正則化參數。所以采用L曲線法,實際上就是為了求出曲線相交處的位置。
自適應的離散L曲線算法的關鍵之處就是適量的移除曲線上的點,來盡可能快速地找到該曲線的相交處。自適應算法的流程如下:
Step1 初始化處理,將所有殘差項和正則化解為0的點進行移除。
Step2 選出所有的轉折點。
Step3 選出真正的相交處。
本文基于L曲線曲率最大的規則即曲線是二次可微的,求解最大曲率點K(μ):
(30)
式中:ρ=‖Axu-b‖2,η=‖xμ‖2,ρ′表示的是對μ求導。但如果采用的正則化方法求得的正則化參數是非連續變動的,則該曲線不可微,所以不能直接求出曲率,需要利用一條曲線去擬合這些離散點去選取正則化參數,接著再尋找相交處的位置,然后從離散點中選擇離擬合曲線相交處最近的點,這個點就是最佳正則化參數。
分數階理論中出現了不同定義的分數階函數,利用其中的Grümwald-Letnikov(G-L)定義構造分數階梯度算子。一般意義下的二次項系數定義為
(31)
式中:
(32)
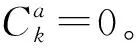
(33)
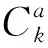
(34)
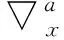
(35)
(36)
分數階可以表示為
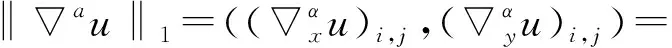
(37)
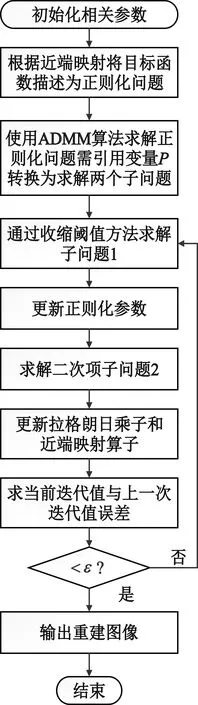
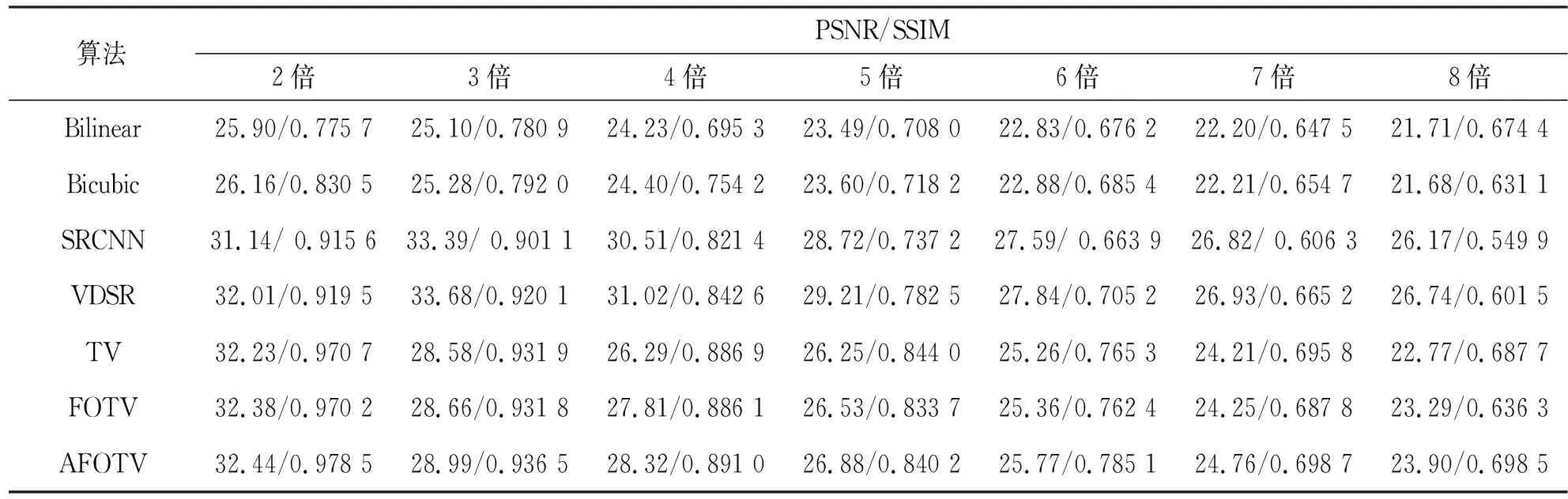
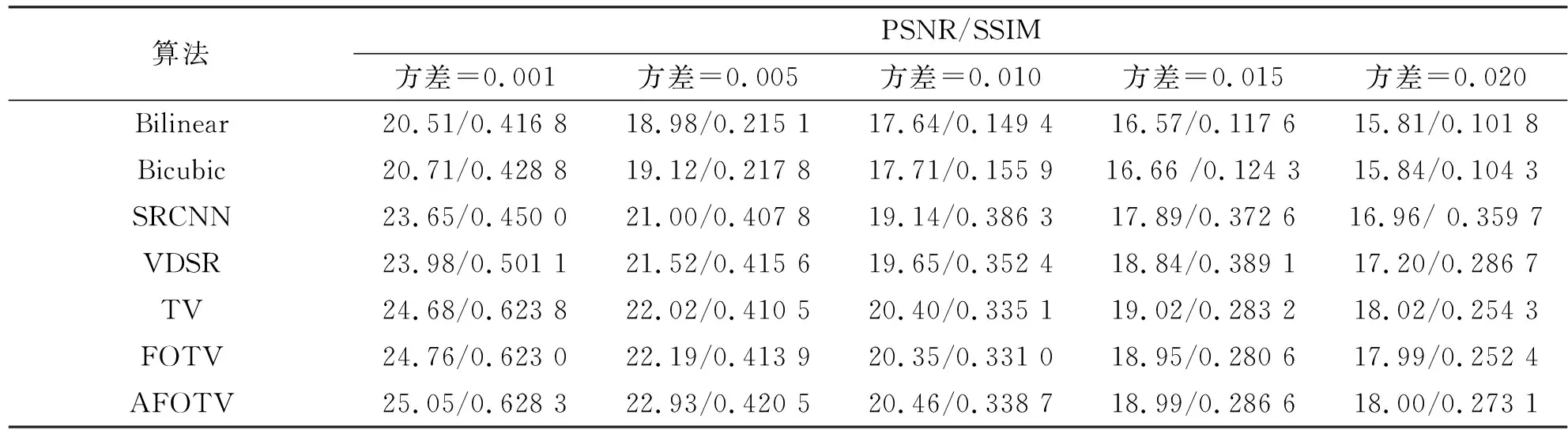
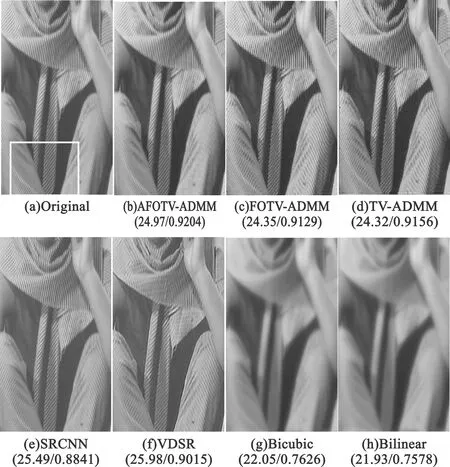
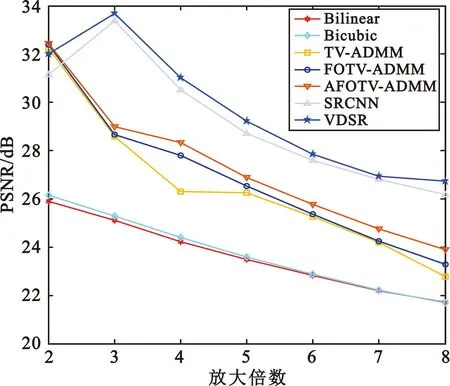
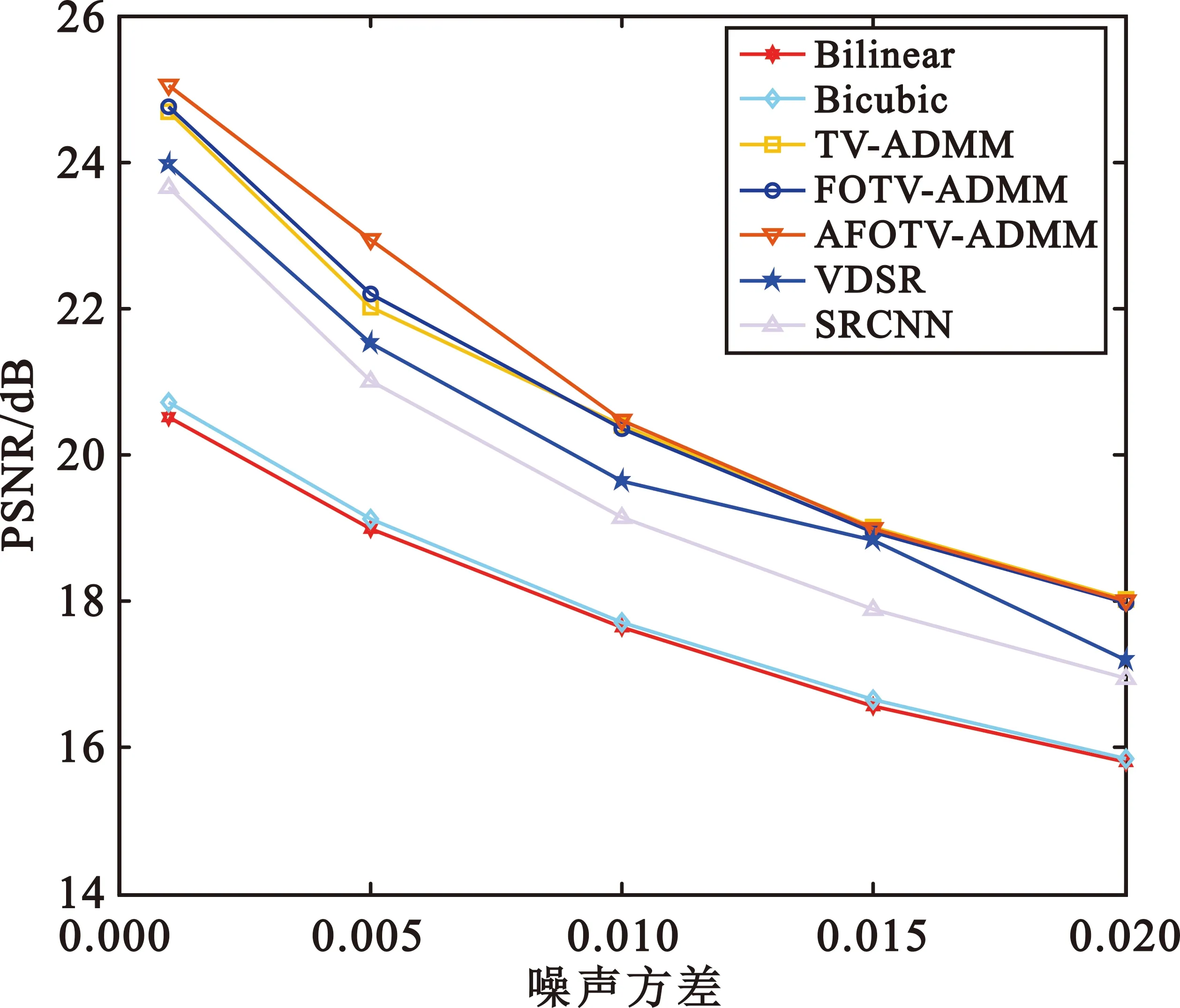
其中根據分數階不同階次的幅頻曲線,a的取值范圍為1 在求代價方程(15)最小值的過程中,基于G-L定義選取分數階作為正則項約束,重建問題(15)表示為 (38) (39) A=u-μHTDT(DHu-Y)。 (40) 類似于全變分求解,根據分數階的約束問題,本文使用ADMM算法求解,引入變量p表示au,原目標問題變為有約束的優化問題: (41) 對于分數階優化問題,其增廣拉格朗日乘子函數 (42) ADMM算法將問題(41)轉換為兩個子問題求解。 (1)子問題1:固定u求p (43) 可以通過收縮閾值方法求解子問題1: (44) (2)子問題2:固定p求u 子問題2的求解中涉及到正則化參數μ的選取。根據正則項變化連續,本文首先計算該點曲率K(μ),將其設置為最大曲率點K(μ)max,與之后迭代過程中通過殘差項計算曲率再更新參數μ。 (45) 問題(45)等價于 (46) 使用快速傅里葉變換處理公式(46),得 (47) 更新拉格朗日乘子和近端映射算子: λk+1=λ-γβ(pk+1-au), (48) Ak+1=u-μk+1HTDT(DHu-Yk+1) 。 (49) 基于參數自適應的FOTV-ADMM算法流程如下: Step1 初始化ε=1×10-4,γ=2,μ=0.000 3,β=0.008,a=1.2,Y0=Y,u0=FillUnknown(Y)。 Step2 計算Ak+1=uk-μHTDT(DHuk-Yk)。 Step4 引入變量p=au。 Step6 更新正則化參數μk+1。 Step8 迭代更新λk+1=λk-γβ(pk+1-uk+1),Yk+1=Yk+(Y-DHuk+1)。 Step9 若‖uk+1-uk‖2≤ε停止迭代。 Step10 輸出uk+1。 其中ε為迭代終止閾值,在本文中的u0由Y采用雙線性插值方法填充得到。本文算法均可通過matlab/C++編程實現。算法流程圖如圖2所示。 圖2 算法流程 選取Matlab2014b作為軟件仿真平臺,深度學習對比算法環境為Window7+caffe架構+cuda6.0+NVIDIA333.11。分別選取Lena(512×512)、Lena(256×256)、Baboon(512×512)、Caneraman(256×256)、Barbara(512×512)、Pepper(490×490)、Girl(280×280)作為2倍超分辨率圖像的實驗原圖,如圖3所示。 圖3 原始超分辨率圖像 超分辨率圖像重建的結果往往依靠人眼視覺來判斷,因人而異,作為主觀評價,不能做到統一。 在選擇重建效果評價標準上本文選擇峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和結構相似性度量(Structural Similarity,SSIM)兩種公認客觀的評價指標來證明本文提出方法的有效性,兩種指標越大就代表重建的效果越好[16]。 實驗選取圖1的5幅原始圖像來做2∶1等間距下采樣,之后以2倍超分辨率來進行實驗,對比的算法為Bilinear Interpolation雙線性插值法、Bicubic interpolation雙三次插值法、深度學習算法SCRNN和VDSR算法、TV-ADMM和FOTV-ADMM以及基于L曲線調參的FOTV-ADMM算法(簡寫為AFOTV),模糊核選取高斯模糊。表1為在2倍超分辨率下各算法的客觀實驗效果對比,表2為Lena512在不同算法下2~8倍數超分辨重建實驗結果,表3為選取Cameraman256灰度圖像加入高斯噪聲均值為0方差從0.001~0.02變化的高斯噪聲各算法的重建實驗結果對比,所有實驗迭代次數為50次。由于篇幅限制只選取部分主觀實驗結果展示,圖像Lena512帽子邊緣細節圖對比分析如圖4所示,Barbara衣服紋理部分如圖5白框標注所示。圖6為Lena512圖L曲線參數調節結果 表1 2倍超分辨率各算法的PSNR和SSIM值對比 單位:dB 表2 Lena(512)2~8倍放大的各方法PSNR和SSIM值對比 單位:dB 表3 不同方差的高斯噪聲下各算法的PSNR和SSIM值對比 單位:dB 圖4 2倍超分辨率Lena帽子細節圖實驗效果展示 圖5 2倍超分辨率Babara圍巾細節圖實驗效果展示 圖6 Lena512圖L曲線參數調節結果 (a)不同放大倍數下各算法重建PSNR值曲線 (b)不同噪聲下各算法重建PSNR值曲線圖7 各算法在不同條件下重建效果曲線圖 圖7(a)為TV-ADMM和FOTV-ADMM算法以及AFOTV-ADMM算法細節放大圖。從主觀實驗圖中可以看出在Lena帽子的邊緣和頭發的紋理細節上FOTV重建的圖像比其他方法重建圖像更清晰,細節保留效果TV-ADMM法容易丟失部分圖像細節紋理信息,帽沿邊緣羽毛出現過平滑現象;Bilinear法整體效果較模糊、細節不清晰;Bicubic從Barbara細節圖上的紋理效果重建來看稍遜于AFOTV和算法。 FOTV模型算法有獨特的幅頻特性優勢,能很好地保留圖像邊緣特征,更多的圖像紋理信息也能保留,有提升高頻的作用,中頻也隨之增強,非線性保留低頻部分。利用分數階不僅能保持圖像邊緣特征,對于處理平滑區域內灰度變化小的紋理細節信息也有很好的效果。TV模型是比較經典的模型,現實生活中,很多信號是非線性不連續的,這種約束方法常常模糊圖像的邊緣。AFOTV模型通過L曲線調節正則化參數,使復原圖像邊緣更加清晰,紋理部分也更接近原始圖形,更好地保留了圖像紋理信息。深度學習算法在圖像亮度方面的改善是比較明顯的,信噪比(Signal-to-Noise Ratio,SNR)值也有比較好的表現,但整體由于深層卷積操作,求解最優均方誤差(Mean Square Error,MSE)還是會帶來過平滑現象,對細節的恢復也存在一定問題。VDSR算法采樣殘差網絡的思想加速了網絡學習速度提升了效率能獲得穩定效果,但總的來說深度學習算法學習要求時間較長,設備性能要求普遍較高。 由表2可知,放大倍數越大,AFOTV算法處理的峰值信噪比值也更大一些。圖6中AFOTV算法在2倍放大時處理效果較佳,結構相似度的值要比TV算法大;在其他倍數,較深度學習網絡有較大的差距,但結構相似度性上表現更好。表3和圖7表明,在噪聲較大的時候得益于TV的過平滑重建現象,TV的去噪能力較其他幾種算法好,但對細節的還原度上有待改進;FOTV和AFOTV算法對紋理細節恢復較好,但在對高頻噪聲抑制方面性能還有待提升。 圖像中灰度變化較緩慢的區域對應低頻平滑部分,TV-ADMM算法對于圖像低頻信號的重建有較好的效果,但由于圖像邊緣的灰度值變化快,將連續高頻率的光滑細節處理成分段等值信號容易出現階梯效應和過平滑現象。本文提出的FOTV-ADMM算法實驗結果表明,該算法適合于邊緣比較銳利陡峭的圖像,防止出現過平滑現象的同時能有效保留圖像的細節和結構相似度。對于灰度值變化快的區域,增大正則化參數有利于提升重建質量但不能過大造成平滑,L曲線的調節選參不同于傳統手動調參算法,能有效改善重建質量,在國防監控,醫學診療圖像恢復等領域具有較大的實用價值。下一步將在降低算法復雜度和減少訓練時間上開展更多的研究應用。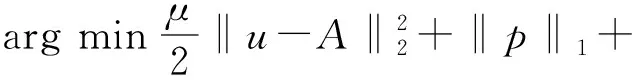
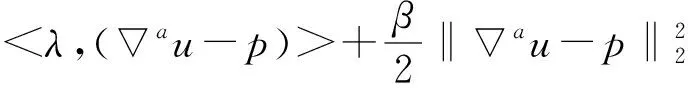
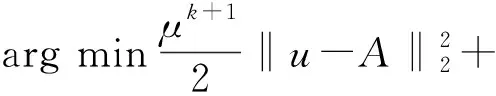
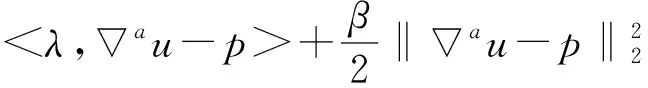
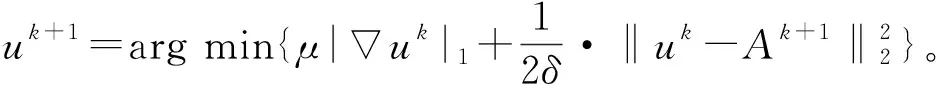
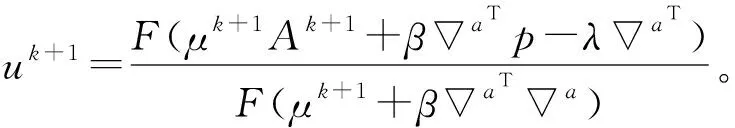
3 實驗與結果分析
3.1 實驗設置及評價指標

3.2 各圖像的2倍超分辨率重建結果對比


4 結束語

