接收機畸變對輻射源個體識別中調制器指紋特征的影響*

史萌愷，黃淵凌，王桂良

(1.戰略支援部隊信息工程大學 信息系統工程學院，鄭州 450001；2.盲信號處理國家級重點實驗室，成都 610041)

0 引 言

輻射源個體識別(Specific Emitter Identification,SEI)技術在無線安全[1]、電磁頻譜檢測、認知無線電[2]以及自組織網[3]中有著廣泛的應用。該技術通過提取射頻信號與硬件相關的射頻指紋特征(Radio Frequency Fingerprint,RFF)，實現對特定輻射源設備的識別，因此能夠不依賴于信號內涵實現對發射設備的識別。但是，SEI所使用的特征在信號中的表現普遍比較細微，因此很容易受到接收機自身硬件特性的影響。這一特性為廣域運動目標識別、多平臺協同識別、識別特征庫遷移等應用帶來了很大的困難。因此，通過分析接收機畸變對RFF的影響，在接收機設計階段就考慮抑制其影響是一項具有很高現實應用意義的研究。

現有的SEI技術主要可以分為兩類[4]：基于輻射源機理的SEI和基于機器學習的SEI。基于輻射源畸變機理的SEI主要是通過分析輻射源指紋特征的來源和產生機理、構建機理模型或數學表示、估計畸變參數的方式來獲得輻射源指紋特征，常用的畸變機理模型有射頻振蕩器畸變模型[5]、功放非線性畸變模型[6]、正交調制器畸變模型[7]等，常用的數學表示有Hilbert-Huang變換[8]、離散小波變換[9]、調制星座圖[10]等。基于機器學習的SEI主要是借鑒語音處理以及圖像識別領域的識別方案[11-12]，利用近幾年機器學習的理論成果來進行特征提取和識別，主要使用的算法有卷積神經網絡(Convolutional Neural Network,CNN)和深度殘差網絡等，但兩種技術路線均無法回避接收機畸變對特征產生的影響。接收機本質上是發射機的逆過程，其含有同輻射源畸變類似的不理想畸變，因此獲得的RFF中普遍含有輻射源和接收機的耦合特征，在更換接收機后無法保證特征的穩定性[13]。對比兩種技術路線，研究這一問題時機理模型在一些方面更具優勢：機理模型獲得的指紋特征經過了人工設計，具有天然的可解釋性，但現有的針對機理的研究中，對接收機畸變進行探討的相關文獻比較少見，尚未形成針對接收機畸變的成熟解決方案。

為了解決以上問題，本文以調制畸變模型為主要研究對象，推導得到了接收機畸變與調制畸變特征的關系，并與實際接收機設計指標相對應，對接收機設計指標提出了建議。通過仿真實驗和實際設備實驗可以證明，本文討論結果具有良好的適用性。

1 基于調制畸變的輻射源個體識別方法

本節對一種典型的基于調制畸變的SEI方法進行介紹。文獻[14]提出了一種基于機理的畸變估計方法，該方法可以對增益失衡、正交錯誤、延遲失配、載波泄露進行聯合提取，效果較好，并在實際輻射源識別中得到了應用。本文將基于此模型進行分析。

基于機理模型的SEI的基本思路是，建立一個合理的含畸變信號模型，之后利用接收信號和解調結果對模型中的畸變參數進行估計。首先，需要建立用以描述畸變的復基帶信號模型：

z(t)=ej(2πf0t+φ)(μ1ρ(t)+μ2ρ*(t)+ξ) 。

(1)

式中：f0為剩余頻偏，ξ為載波泄露，φ為信號初相，ρ(t)為復基帶調制信號，μ1、μ2為描述了增益失衡以及正交錯誤的畸變參數。

(2)

式中：cn為傳輸符號，h(t)為成形濾波器，T為采樣周期，τ為采樣延遲，τd描述了I、Q兩路之間的延遲，該延遲可以通過滑動相關來消除。

(3)

(4)

式(3)、(4)中：GI/Q描述了I、Q兩路的增益失衡，ζ描述了正交錯誤。

根據式(1)所描述的模型，在接收端進行定時估計和匹配濾波后，可以建立在最佳采樣點處的接收信號模型：

(5)

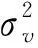
U(f0)Hr=Gθ+v。

(6)

對式(6)應用最大似然估計得到θ的估計結果為

(7)

式(7)中的頻偏可以利用快速傅里葉變換(Fast Fourier Transform,FFT) 等傳統頻率估計方法得到，本文不再贅述。在得到畸變參數矢量θ的估計值后，為了消除初相和信號幅度的影響，同時獲得各調制畸變特征的估計值，可以根據式(3)、(4)得到增益失衡和正交錯誤的估計值：

(8)

(9)

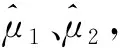
(10)

經過以上步驟，即可根據接收信號和解調符號得到對載波泄露和其他調制畸變的估計結果，但該模型并沒有考慮接收機畸變對特征值的影響，針對這一問題需要進一步討論。

2 接收機畸變對調制畸變估計結果的影響

2.1 濾波器畸變的基本機理

接收機畸變可以分為確定性畸變和隨機性畸變，前者主要指接收機放大器和濾波器不理想造成的線性和非線性畸變，后者主要包括各類噪聲。隨機性畸變可以通過對單一接收機的優化得到改善；在跨接收機識別過程中，需要考慮的主要影響因素為不同接收機之間確定性畸變的差異[15]。

圖1給出了超外差結構接收機的基本結構，接收機確定性畸變主要來自于接收通路上在射頻和中頻模塊中包含的多個濾波器的不理想特性、多級功放的非線性畸變、接收機頻率源不理想、IQ通道畸變。其中，頻率源特性受工作環境影響，能且僅能通過提高頻率源設計要求來減小其影響；IQ通道畸變僅存在于零中頻結構接收機中，可以通過使用非零中頻結構接收機來進行回避。因此，本文優先考慮接收設備濾波器畸變和功放非線性對載波泄露的影響。

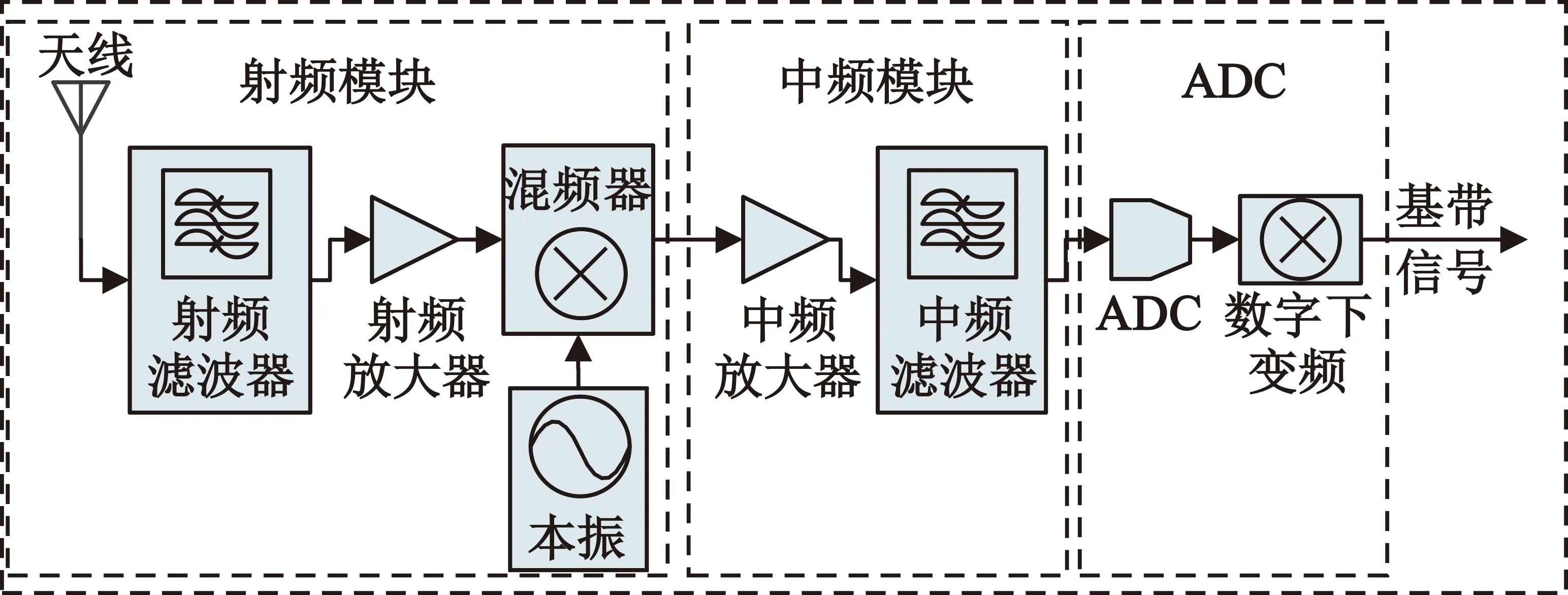
圖1 超外差接收機基本結構

為了便于分析，可以將各項器件畸變進行簡化，將接收機的濾波器特性等效為單個等效濾波器，將功放畸變等效為單個功放，得到簡化模型如圖2所示。

圖2 接收機等效模型

該模型中放大器和濾波器的先后順序會對結果產生影響，本文采用放大器在前、濾波器在后的形式，理由是：大多數接收機射頻模塊采用的濾波器帶寬很大，其帶內抖動比較輕微，因此射頻部分的畸變主要表現為射頻放大器非線性畸變；而在中頻模塊，濾波器帶寬較窄，帶內抖動更加明顯，且中頻放大器線性程度較好，因此中頻部分的畸變主要表現為濾波器線性畸變。綜上所述，使用圖2所示結構能夠更加貼近實際接收機畸變情況。

2.2 含接收機畸變的接收信號模型

首先考慮功放非線性。當輸入信號為窄帶信號時，功放非線性可以使用泰勒級數模型來進行描述，即

(11)

式中：λk為非線性系數，x(t)、y(t)分別為系統的輸入和輸出。隨著階數升高，系數λk減小，因此高階次項的影響很小，在接下來的推導中忽略式(11)中階次高于3的部分。設輸入信號x(t)=A(t)·cos(ω0t+φ)并代入式(11)，則有

y(t)=λ1x(t)+λ3x(t)3=

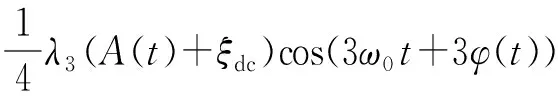
(12)

由于接收通路中各濾波器的存在，可以將式(12)中的倍頻成分忽略，將余下部分轉換到基帶。為了便于分析，只考慮采樣點處的信號，并且令λ1=1。將式(5)所示的信號進行幅度歸一化后代入，可得

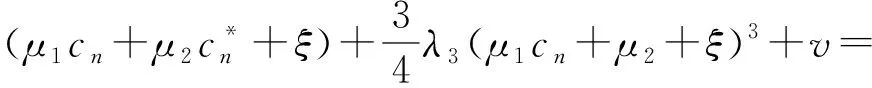
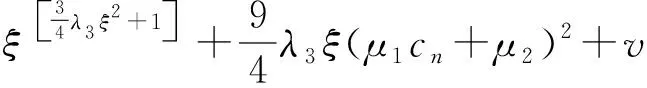
(13)

z(n)=y(n)?hr(n)=

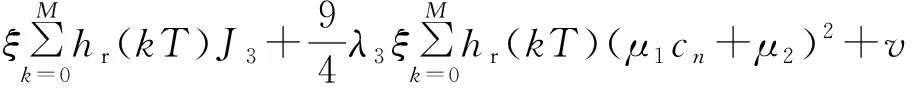
(14)

將式(14)改寫為矩陣形式：

(15)

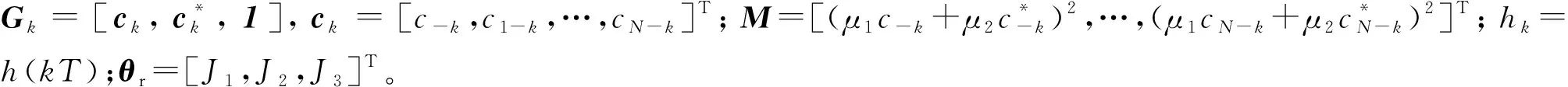
式(15)即為含接收機畸變的接收信號模型。接下來，可以根據式(15)討論機理模型的估計結果。

2.3 接收機畸變對估計結果的影響

對式(15)所示的信號模型，采用2.1節中介紹的調制畸變估計方法進行特征估計，將式(15)代入式(7)，得到估計結果：

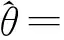
(16)

(17)

將式(17)代入式(16)，可得

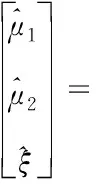
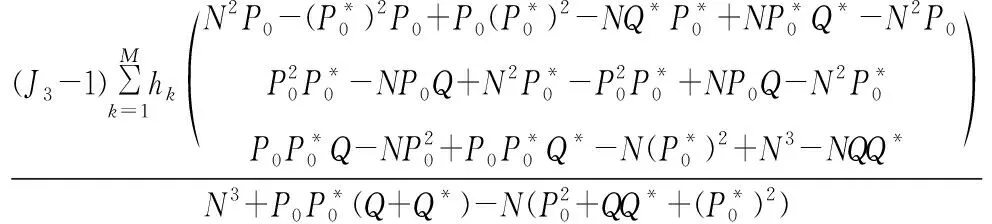
(18)

根據式(18)即可推算傳統模型估計結果與特征真值的關系。令N→∞，計算各估計結果的期望，當發送符號位隨機序列時，Pk、Q、R、S均為有界量，因此可得最終結果為

(19)

式(19)說明，考慮接收機畸變影響后，調制畸變特征估計結果中的IQ增益失衡和正交錯誤仍是其真實值的無偏估計，而載波泄露的值則會同時受到線性畸變和非線性畸變的影響。

2.4 接收機設計指標與接收機畸變參數的關系

濾波器設計指標：實際接收機設計的主要濾波器指標為帶內抖動。根據式(19)，濾波器信號頻點處的幅相響應會對載波泄露估計結果產生影響，但在接收機設計指標中的帶內抖動指濾波器通帶內的波動程度，其值一般大于信號頻點處的抖動。為了不失嚴謹性，不妨設定濾波器在信號頻點處的抖動等于其帶內抖動。

非線性設計指標：實際接收機設計過程中，一般使用三階互調抑制IMR3作為接收機非線性指標，其值可以與λk進行對應[21]：

(20)

式中：vs為輸入電壓。

至此，可以將接收機設計參數與估計結果聯系起來，得到

(21)

式(21)描述了載波泄露估計結果的偏移程度與目標載波泄露真實值ξ、三階互調抑制IMR3、輸入信號電平vs、濾波器抖動J的關系。由于濾波器抖動會大于信號頻點處抖動，因此得到的理論偏移程度會偏大，即得到的設計指標會在滿足需要的前提下更加嚴格。在實際接收機設計過程中，可以根據接收機工作狀態對估計結果的偏移進行估算，進一步確定具體設計指標。

根據2.1節中的討論，接收機其他設計指標對調制器畸變影響微小，因此在設計階段不需要進行特殊要求。

根據以上結果，結合實際接收機設計經驗，本文認為，通過接收機設計來保證不同接收機之間的特征一致性是可行的，在第3節的設計實例中將進一步證明這一點。

3 仿真與實驗

3.1 實驗描述

3.1.1 接收機畸變的生成

利用下式生成含有不同畸變的接收機濾波器[16]：

G(f)=H(f)A(f)jφ(f)。

(22)

式中：A(f)和φ(f)分別表示濾波器頻率響應的幅度畸變和相位畸變。將其展開為傅里葉級數的形式，并忽略高階項，可以得到

A(f)=a0+akcos(2παkf)，

(23)

φ(f)=2πb0f+bksin(2πβkf) 。

(24)

通過指定αk、βk、ak、bk的值生成具有不同頻率響應的接收濾波器。設定濾波器階數為800階，按照表1參數仿真產生具有不同頻率響應的濾波器，表中同時給出了各濾波器在中心頻點(即仿真信號頻點)的抖動值。

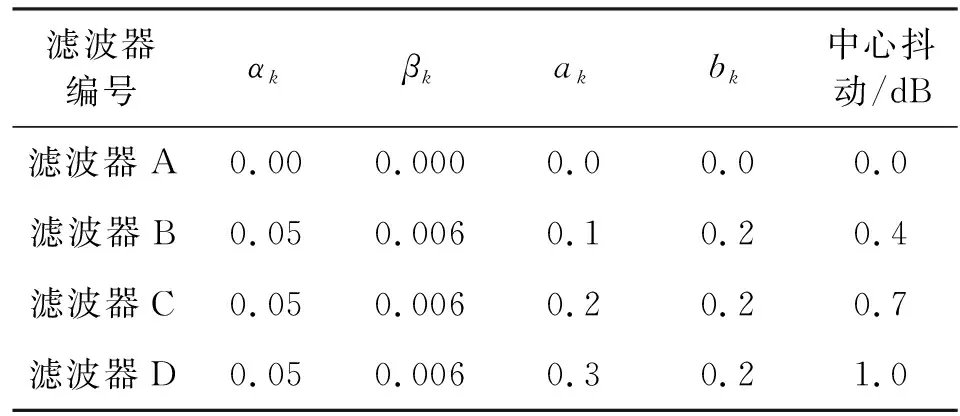
表1 濾波器生成參數設置

非線性特性可以利用式(11)，通過設定不同的λk來生成。

3.1.2 信號仿真設置

仿真信號調制方式為正交相移鍵控(Quadrature Phase Shift Keying，QPSK)，發送符號為隨機序列，符號速率1 MHz，信號載頻2 MHz，采樣率8 MHz。在生成發射星座點時疊加載波泄露和調制畸變，載波泄露值ξdc=0.01+0.01i，IQ增益不平衡GI/Q=0.05，正交錯誤ζ=0.05，信號信噪比設置為30 dB。生成信號先疊加非線性畸變，之后通過畸變濾波器。非線性畸變按式(11)生成，僅考慮三階非線性，通過改變λ3來改變畸變大小。在接收階段，對信號進行時間同步和相位同步后，以每20 000個符號作為一次估計的輸入樣本進行特征提取。

3.1.3 結果評估方法

估計結果主要采用特征偏移量來進行定量描述，特征偏移量具體定義如下：

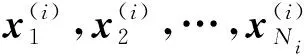
(25)

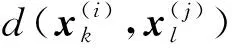
根據本文的分析，載波泄露的特征偏移量與載波泄露特征值本身成正比，因此為了能夠直觀描述偏移量的大小，樣本在計算偏移量之前應當進行歸一化，具體方法是將估計值除以其對應的載波泄露真實值的模，其值的大小表示了偏移值與特征實際值的比值。

3.2 實驗結果

根據3.1節中的仿真設置生成信號并進行特征提取，得到不同參數下的估計結果。圖3和圖4分別給出了調制畸變特征提取結果和載波泄露特征提取結果相對于實際值的偏移量，同時也給出根據計算得到的理論估計值。圖中各點均根據特征實際值進行了歸一化。

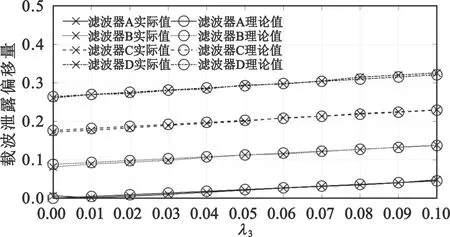
圖3 不同濾波器及不同功放非線性參數下載波泄露特征實際偏移量與理論值的對比

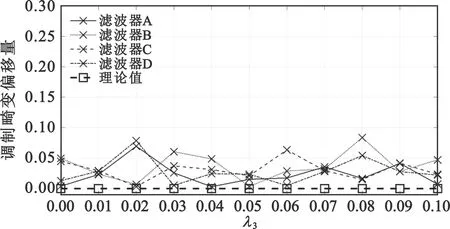
圖4 不同濾波器及不同功放非線性參數下調制畸變特征實際偏移量與理論值的對比

圖3顯示，濾波器畸變及功放非線性均會對載波泄露特征產生影響，其影響與理論推導結果非常相近。圖4顯示，調制畸變與濾波器和功放非線性的改變并無關系，其偏移量不超過真實值的10%，屬于比較輕微的范圍，這與理論推導結論相一致。

從仿真信號特征提取結果中可以看出，載波泄露和調制畸變兩項特征受接收機畸變的影響與推導結果有很高的一致性。

3.3 接收機設計實例

根據第2節中的分析，本文認為，通過接收機設計來保證不同接收機之間的特征一致性是可行的，因此本文依據該結果對接收機設計進行了實踐，并得到了特征提取結果。

在接收機設計階段，對接收機帶內抖動和非線性指標提出要求。接收機為超外差結構，中頻頻率為70 MHz，相關指標如表 2所示。根據2.1節的討論，在使用非零中頻的接收機時，除以上指標之外的其他指標不需要進行額外要求。

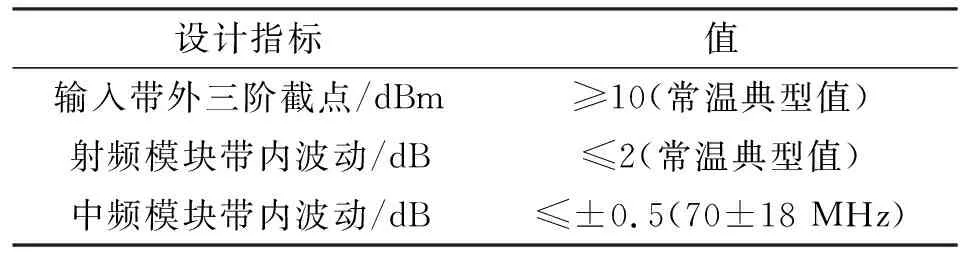
表2 接收機帶內抖動及非線性指標

值得一提的是，由于射頻模塊濾波器帶寬較寬，其帶內抖動將遠大于中心抖動，如果必要，在設計中可以不對射頻模塊帶內抖動進行額外要求。

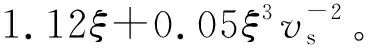
使用2臺X310型和5臺B210型USRP軟件無線電平臺作為輻射源，發射載頻為1 GHz、符號速率1 MHz的QPSK信號。使用依據表 2參數設計的兩臺接收機分別對信號進行接收，接收機采樣率設置為80 MHz。特征預處理參數與3.1節的設置一致。在獲得特征提取結果后，利用支持向量機(Support Vector Machine,SVM)分類器進行分類，統計正確率。分類器輸入特征為載波泄露實部和虛部。特征提取結果和識別正確率分別如圖5和圖6所示。

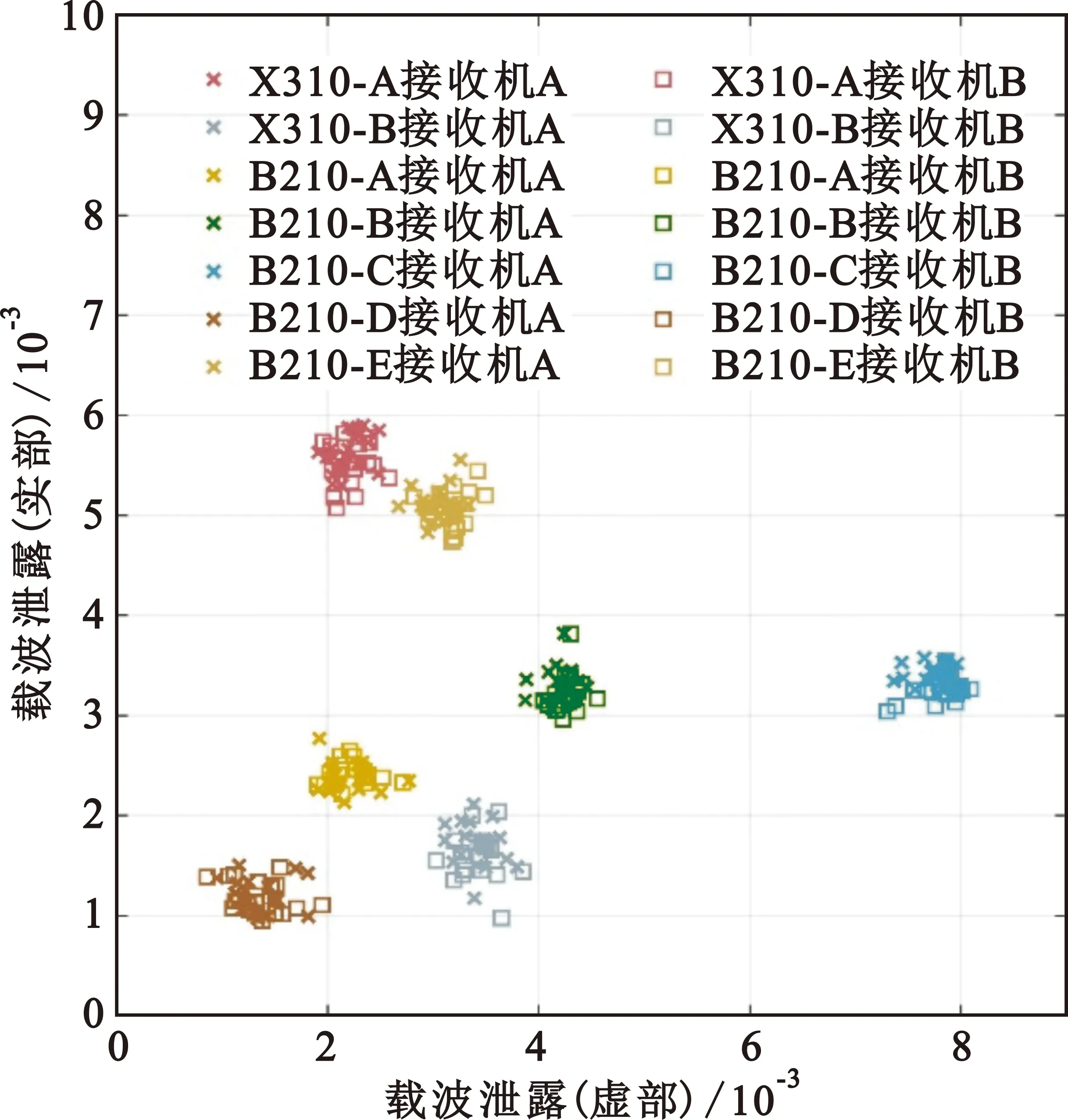
圖5 兩臺接收機的載波泄露特征提取結果對比

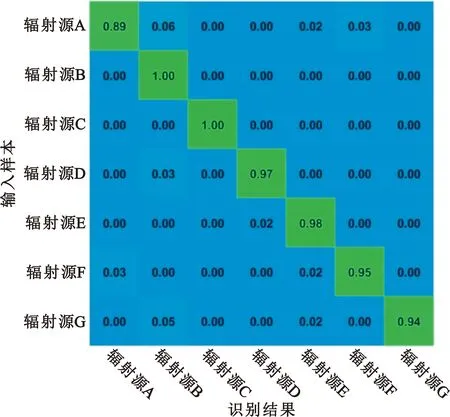
圖6 以兩臺接收機獲得的信號分別作為訓練集和測試集的識別正確率

圖5顯示，兩臺接收機獲得的載波泄露特征的穩定性較高，特征偏移并不明顯，已經基本可以滿足在不同接收機之間通用的要求。圖6中的識別正確率則進一步證明了這一點，在使用兩臺接收機的接收結果分別作為訓練集合測試集的條件下，平均識別正確率仍然可以達到96.15%。

綜上所述，在跨接收機應用中，通過接收機設計來保證載波泄露和調制畸變特征的穩定性是可行的。

4 結束語

本文分析了在SEI中接收機畸變對調制畸變特征估計的影響，推導得到了非線性畸變以及濾波器畸變與估計結果的數學關系；之后，根據推導結果，將各畸變與實際接收機設計指標相對應，提出了對SEI接收機設計的建議；最后，通過實驗驗證了推導結果的正確性。

在今后的單接收機識別乃至于跨接收機識別應用中，可以采用本文的方法對接收機畸變的影響進行評估，指導輻射源個體識別接收機設計。本文只考慮了調制畸變(含載波泄露)的提取問題，實際識別應用中往往采用多種特征提取模型進行聯合提取，在接下來的研究中可以針對其他特征進行進一步討論。