基于投影對消處理技術的穩健自適應波束形成*

鄧 欣,袁紅剛,婁 寧

(1.中國西南電子技術研究所，成都 610036;2.北方電子設備研究所，北京 100191)

0 引 言

自適應波束形成算法可通過獲取空間環境信息，在期望信號方向形成主瓣的同時自適應在干擾方向形成零陷，實現抑制干擾。這種自適應波束形成技術被廣泛應用于各種不同領域[1-2]。大多數傳統自適應波束形成通常假設工作在理想情況下。實際中，各種非理性因素如陣列自身的幅相誤差、目標波達方向(Direction of Arrival，DOA)估計誤差、干擾方向失配等問題通常會導致傳統波束形成性能下降，其中目標來波方向失配引起的目標方向增益下降問題受到了廣泛的關注和研究[3-5]。

現有的穩健自適應波束形成算法主要包括對角加載算法、不確定集約束算法[6]、最差性能最優化算法[7]以及穩健線性約束最小方差[8]算法等。其中，對角加載算法雖然可以有效提高穩健性，但其性能依賴對角加載因子的選擇，當對角加載因子選取不當時，可能導致干擾方向零陷深度不夠[9]，此外，在信干噪比較大時，對角加載算法可能會出現性能下降問題。不確定集約束算法將可能失配的導向矢量約束在某個橢圓不確定集內，從而降低目標DOA失配的影響。最差性能最優化算法通過優化最差條件下的波束形成性能達到提高穩健性的目的。不確定集約束算法和最差性能最優化方法均可歸結為對角加載類算法，只是有各自的對角因子求解方法，此類方法在信干噪比較高時仍然會出現性能下降較大的問題[9]。穩健線性約束最小方差算法雖然能在一定程度上減少目標期望信號方向失配造成的影響，但當期望信號失配較大時，目標方向的增益仍然會有一定損失。

針對現有算法存在的問題，本文提出了一種基于投影對消處理的穩健波束形成算法，通過尋找協方差矩陣特征向量中與目標DOA估計矢量相關性最強的矢量作為目標導向矢量，并通過投影對消矩陣消去期望信號，最后通過在干擾方向施加零點約束形成零陷。與現有方法的對比實驗驗證了所提算法能在目標方向失配、信干噪比較大的情況下實現穩健波束形成，并在干擾方向形成較深零陷。

1 信號模型

考慮N元等距線陣，其陣元間距為d，且每個陣元均為全向陣元，如圖1所示。

圖1 等距線陣自適應波束形成系統模型示意圖

X(t)=A(θ)S(t)+N(t) 。

(1)

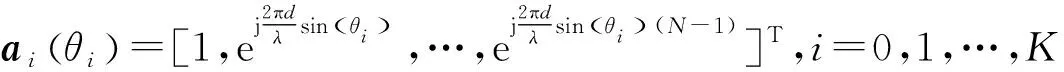
利用式(1)的接收信號，可以得到協方差矩陣的最大似然估計值為

(2)

式中：L為快拍數，上標H表示矩陣共軛轉置。

對于常規最小方差無失真響應波束形成(Minimum Variance Distortionless Response，MVDR)算法，其最優權值為

(3)

2 基于導向矢量不確定集約束的穩健自適應算法及其本質

2.1 算法描述[6]

在實際中，真實的導向矢量a0很難準確獲得，但是可以被約束在某個橢圓不確定集之內，即

(4)

式中：A為某給定參數。為了優化得到更準確的導向矢量s，將波束形成算法代價函數描述為如下形式：

(5)

式中：σ2表示陣列輸出信號的方差。

式(5)中的問題可轉化為二次約束二次規劃問題，并由Lagrange乘子法求解得到最優解s[10]為

(6)

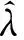
由矩陣求逆引理可以得到

(7)

將式(6)代入采樣矩陣求逆(Sampling Matrix Inverse，SMI)算法的最優權表達式，可以得到穩健算法的最優權為

(8)

這說明該波束形成算法屬于對角加載類算法。由式(7)和式(5)的約束條件可以推出解最優Lagrange常數的公式為

(9)

2.2 算法分析

對式(9)的解進行分析。首先對R進行特征值分解，得到

R=UΣUH。

(10)

式中：U=[u1,u2,…,uN]，為R的特征向量矩陣，Σ=diag(λ1,λ2,…,λN)為相應的特征值矩陣。可以將式(9)展開寫作[10]

(11)

首先做一點近似：在信噪比較高的前提下(通常認為-10 dB以上)，目標信號對應的特征向量與目標信號的導向矢量近似同向，可以用目標信號對應的特征向量代替目標信號的導向矢量，即a0=δu1，δ為一常數。

(12)

式中：γ是一個極小的常數，用以保證協方差矩陣可逆。

由于γ是一個極小的數，因此式(12)的結果可以采用以下近似:

(13)

則方向圖在a0方向的幅度為

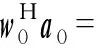
(14)

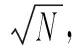
事實上，式(14)的結論在很多其他的對角加載類算法中也能推出，如基于模約束的穩健波束形成算法和基于最壞性能的最優的自適應波束形成算法等。

3 基于投影對消處理的穩健自適應波束形成算法

3.1 目標信號對應的特征向量搜索[7]

由之前的a0=δu1可知，可以用目標信號的特征向量代替目標導向矢量，因此需要對目標信號的特征向量進行搜索[11]。

定義列向量x、y的相關系數為

(15)

(16)

3.2 投影對消處理過程

通過式(16)搜索得到目標信號的特征矢量后，就可以生成相應的對消矩陣:

(17)

經過對消之后的協方差矩陣記為R′:

R′=BRBH。

(18)

將式(18)進行展開:

(I-u1(u1Hu1)-1u1H)H=

(19)

由式(19)可知，R′中關于目標信號的特征矢量已經被濾除，這與對角加載類的穩健自適應波束形成算法等價。為了保證R′的非奇異性，要對其進行補償，即

R″=R′+γI。

(20)

式中：γ為一極小常數。

得到對消后的協方差矩陣后，根據最小均方誤差準則，可以得到此時的最優權為

(21)

則陣列波束形成的方向圖為

(22)

3.3 約束零點位置

式(21)中的權向量是基于SMI算法獲得的，當目標信號功率較大時，該權向量無法在干擾處生成零陷，因此為了保證干擾處零陷的產生，需要對方向圖加入零點約束。

設C為約束矩陣，F為約束值向量，權值wopt應同時滿足

CHwopt=F。

(23)

在這里，由于目標信號的DOA估計不精確，我們不對目標信號使用約束，即C中的約束向量全部是干擾方向的導向矢量，F為全零列向量。

線性約束最小方差(Linearly Constrained Minimum Variance，LCMV)算法是加入零點約束的有效算法，但是直接由式(20)估計得到的協方差矩陣進行LCMV波束形成是不行的，這是由于由式(14)推出的結論是基于SMI算法的，同樣的結果對于LCMV算法并不適用，因此需要另辟蹊徑。

采用正交投影的原理得到相應的權向量。首先，全體滿足Φ={w|CHw=F}的權值w構成C的零空間，因此Φ為一線性子空間，而wopt∈Φ，向C零空間做投影的投影矩陣可以表示為

E=I-C(CHC)-1CH，

(24)

(25)

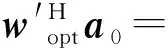
(26)

(27)

所提算法的流程圖可見圖2。

圖2 算法流程圖

算法具體步驟如下：

Step1 對協方差矩陣R進行特征分解。

Step2 以式(16)為準則，尋找與目標估計導向矢量最接近的特征矢量作為目標導向矢量。

Step3 由式(17)生成相應的對消矩陣，并計算式(18)中對消后的協方差矩陣。

Step4 求解零點投影矩陣E，并通過式(25)得到最終的權矢量。

4 仿真與分析

為了對比本文所提的算法與基于導向矢量不確定集約束的穩健自適應波束形成算法、穩健自適應最小方差準則算法和傳統最小方差無失真響應算法的性能差異，證明本文所提算法的有效性，分析幾種算法的優缺點及適用條件，進行了如下三組仿真實驗。設陣元數為16的均勻線陣，陣元間距為半波長，陣元為全向陣元，信號真實波達方向為10°，實驗參數如表1所示。

表1 仿真實驗參數

4.1 不同信噪比情況下性能比較(實驗1)

信噪比分別為10 dB、-10 dB、-20 dB，信干比為-10 dB，導向矢量估計誤差為3°，兩個干擾方向分別是-35°和30°,仿真結果如圖3所示，圖中均以點劃垂直線指示目標方向，垂直實線指示干擾方向(下同)。由圖3可以看出，隨著信噪比變化，本文方法和橢圓不確定集約束算法以及穩健自適應最小方差準則算法均能較好地校正導向矢量失配誤差。其中橢圓不確定集約束算法和本文所提算法在目標方向的增益略好于穩健線性約束最小方差準則算法，但橢圓不確定集約束算法由于沒有加入零點約束，抑制干擾能力不如本文方法，尤其是當信噪比為-20 dB時，橢圓不確定集約束算法未能在-35°干擾方向形成零陷。當信噪比為10 dB時，穩健自適應最小方差準則算法能較好地抑制干擾，但隨著信噪比增大，其零陷深度變淺。相比之下，傳統的最小方差無失真響應算法主瓣偏離，且未能在干擾方向形成較深零陷。

(a)信噪比10 dB

(b)信噪比-10 dB

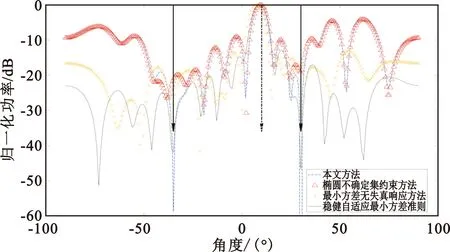
(c)信噪比-20 dB圖3 不同信噪比情況下的方向圖

4.2 不同信干比情況下性能比較(實驗2)

信噪比為15 dB，導向矢量估計誤差為3°，信干比分別為-10 dB、5 dB、10 dB，兩個干擾方向分別是-35°和30°，仿真結果如圖4所示。

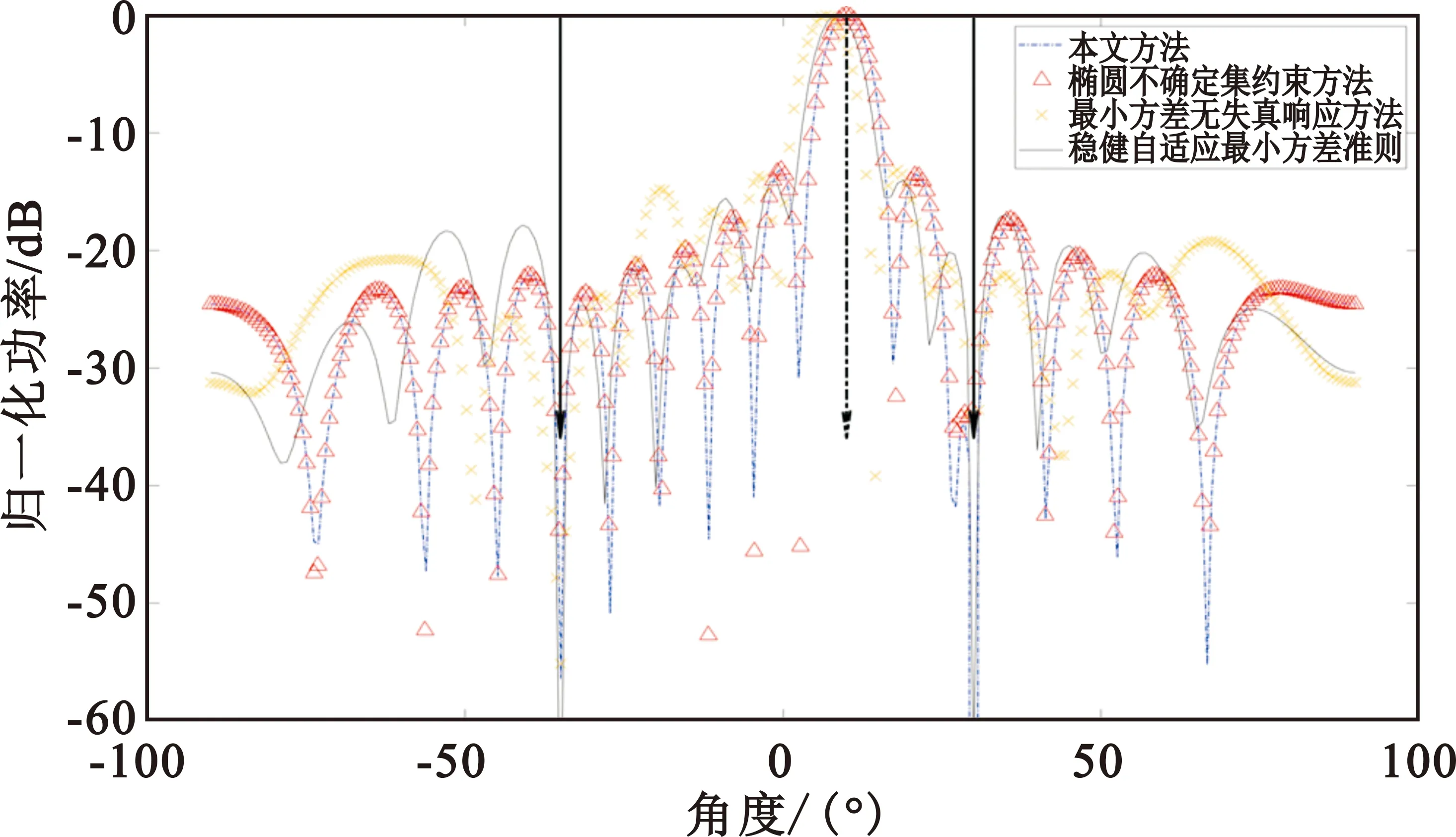
(a)信干比-10 dB

(b)信干比5 dB

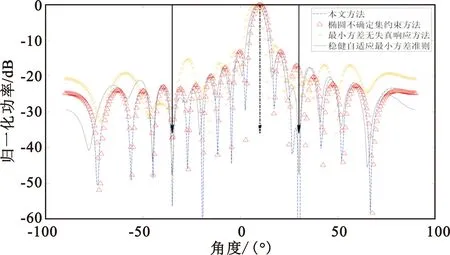
(c)信干比10 dB圖4 不同信干比情況下的方向圖

由圖4可以看出，本文方法和穩健最小方差準則算法均能在干擾方向形成較深零陷，但本文方法形成零陷相對更深。當信干比增大至10 dB時，橢圓不確定集約束算法零陷較淺，抑制干擾能力下降。本文方法和橢圓不確定集約束算法在目標方向均能形成較好的增益，最小方差無失真響應算法在目標方向發生失配，且旁瓣較高。

4.3 不同導向矢量估計誤差情況下性能比較(實驗3)

信噪比為15 dB，信干比為-10 dB，導向矢量失配角度分別為3°、5°和7°，兩個干擾方向分別是-35°和30°，仿真結果如圖5所示。

(a)失配誤差3°

(b)失配誤差5°

(c)失配誤差7°圖5 不同導向矢量估計誤差下的方向圖

由圖5可以看出，最小方差無失真響應算法在存在導向矢量失配誤差時性能會有所下降，失配誤差越大，性能下降越明顯。穩健自適應最小方差準則算法受到失配誤差的影響小于最小方差無失真響應算法。本文方法和橢圓不確定集約束算法均能有效地校正導向矢量失配誤差而與誤差的大小無關，這與之前的分析一致，因為兩種方法的本質都是使陣列在真實目標方向生成最大值，與失配誤差無關。

綜合上述，基于穩健自適應方差準則的波束形成算法能在一定程度上減少目標方向失配產生的影響，但失配誤差較大時性能有所下降。基于導向矢量不確定集約束的穩健自適應波束形成算法與本文方法都能有效地校正導向矢量失配誤差，并且性能與誤差的大小無關；在信干比較小的時候，兩種方法得到的方向圖是幾乎一樣的，這與預期一致，因為本文提出的算法在高信噪比低信干比條件下與基于導向矢量不確定集約束的穩健自適應波束形成算法等價；信干比較高時，也就是說目標信號功率相對較大的情況下，基于導向矢量不確定集約束的穩健自適應波束形成算法由于沒有零點約束，因此在干擾方向上不能有效形成零陷，而本文提出的算法由于進行了額外的零點約束，所以在干擾方向生成了有效的零陷；兩種方法隨信噪比下降均有旁瓣升高的問題。

5 結束語

本文綜合考慮目標來波方向估計不準確引起的傳統自適應波束形成性能下降的問題，以及基于導向矢量不確定集約束的穩健自適應波束形成算法無法在目標信號功率過高的情況下在干擾處生成零陷的問題，從基于導向矢量不確定集約束的穩健自適應波束形成算法出發，推導其原理，進而提出了基于投影對消預處理的穩健波束形成算法。該算法通過正交投影方式進行零點約束，可有效校正導向矢量失配誤差，且在不同信干比情況下均能在干擾方向生成較深的零陷。仿真結果驗證了該算法的有效性。該算法可用于數字相控陣天線的自適應波束形成，在實際應用環境中目標信號方向估計不準的情況下，確保來波方向處理性能的同時有效抑制旁瓣干擾。在所提算法的基礎上，未來還可以進一步研究在低信噪比條件下壓制方向圖旁瓣的方法，解決旁瓣隨著信噪比降低而升高的問題。