順序旋轉圓極化相控陣的交叉極化抑制*

溫 劍，黃中華，姚亞利，張 云，王軍會，侯祿平，梁宇宏

(1.中國西南電子技術研究所，成都 610036；2.中國人民解放軍93129部隊，北京100843)

0 引 言

電磁波的極化傳播特性是影響衛星通信星地鏈路性能的重要因素。在低于3 GHz的頻段，主要考慮電離層等離子體受地磁場影響，對沿磁場方向傳播的線極化電磁波造成的法拉第旋轉效應[1]。而在高于12 GHz的頻段，還應考慮大氣層中的雨滴或冰晶對電磁波的去極化效應。由于圓極化電磁波具有較好的抗法拉第旋轉和去極化效應的特性，所以在衛星通信系統中多采用圓極化天線。

Ka頻段寬帶衛星通信由于其高通量、小型化終端的優勢，成為寬帶衛星通信的主要發展方向。Ka頻段寬帶衛星網絡的體制、地面終端、測控站、衛星載荷、元器件等各方面都成為研究熱點，推動了技術和商業的迅速進步。在Ka頻段寬帶衛星通信網絡體系中，星載業務天線、星間鏈路天線、饋電天線及地面終端天線全面采用圓極化有源相控陣天線，將通信能力和使用便捷性大幅提升。Ka頻段有源相控陣天線是寬帶衛星網絡工程研究的焦點。

除了專用的極化自適應雷達相控陣天線[2-3]，常規的相控陣天線系統設計時通常將陣列的極化方向圖分解為天線單元電場方向圖(矢量)和陣因子方向圖(標量)的乘積。常規陣列要實現較好的極化特性，首先要優化陣元極化特性，采用結構簡單、對稱性高、互耦小的陣列單元實現良好的交叉極化抑制；其次要對陣因子的交叉極化特性進行設計。Teshirogi[4]和Huang[5]提出了陣列單元順序旋轉并配合移項補償的技術，可以采用軸比較差的橢圓極化單元甚至是線極化單元合成寬帶圓極化陣列。這種技術在圓極化相控陣中得到廣泛應用。Huang的論文推導了采用4個線極化單元作為子陣合成圓極化陣列的矢量疊加公式。但利用這套算法在進行大規模陣列優化時計算量過大，而且公式中采用的單元方向圖未計入互耦，實際意義有限。

雖然工程中大量應用了順序旋轉技術，但鮮有文獻對各種順序旋轉方式進行交叉極化特性詳細分析對比。常用的正方形2×2子陣旋轉方式可以在天線法向及小掃描角范圍內形成非常高的交叉極化比，但在大角度掃描區域存在交叉極化分量柵瓣。由于早期的通信相控陣多應用在同步軌道衛星平臺，其掃描角度通常小于15°，所以交叉極化柵瓣的問題不突出。

當前低軌衛星通信網絡領域發展迅猛，星載相控陣天線的工作帶寬、掃描角度越來越大，寬角寬帶范圍內的交叉極化抑制必須得到有效抑制才能消除空間中有意或無意的干擾。另外，工程中采用多頻段共孔徑的技術減小設備體積，采用頻率選擇表面實現低可探測，這些眾多不斷加嚴的設計約束使得相控陣天線單元越來越復雜、緊湊。特別是在毫米波頻段相控陣天線單元的加工誤差大、介質材料參數離散度高，陣元在陣中的諧振頻率、極化、阻抗特性發生惡化偏移。所以，采用理論及全尺寸三維電磁場仿真等多種手段，預計實物樣機的技術風險，是設計中的關鍵控制點。但面對毫米波通信相控陣天線成百上千元的規模，全尺寸電磁仿真的未知量和計算量巨大，難以適應高速推進的工程項目。開發一種高效快速的大規模陣列極化輻射特性的算法顯得尤為重要。

本文在Ka頻段有源相控陣天線多項前期研究基礎上，介紹采用順序旋轉方法設計的大規模有源相控陣天線的極化合成理論研究成果及工程應用案例。

1 相控陣的順序旋轉圓極化設計

1.1 常規順序旋轉的原理及仿真案例分析

Huang[5]首次提出的正方形2×2子陣順序旋轉方式，是將4個線極化單元繞中心依次以90°的增量旋轉，其激勵相位也依次相差90°，改變相位差的正負，可以形成左旋或右旋圓極化。順序旋轉方法可以極大提高陣列的極化純度、軸比帶寬，降低對單元的設計要求。Huang在文獻[5]中也對2×2陣列交叉極化特性做了理論分析，給出了部分剖面、部分指向的交叉極化特性，指出這種順序旋轉方式存在較高交叉極化柵瓣的區域，但未對大型陣列在大角度掃描區域的柵瓣特性進行詳細論述，也沒有提出有效的抑制手段。以下用全尺寸電磁場仿真復現順序旋轉陣列的交叉極化問題。

圖1所示的算例1為工作在26.75 GHz的8×8正方形網格陣列，其左右旋圓極化可變，掃描范圍為60°半錐角。采用具有寬角高增益、高隔離度的帶腔金屬線極化偶極子單元，通過調整饋電相位來實現極化旋向的切換。采用HFSS軟件進行仿真。將上半空間的三維方向圖數據導出，繪制成UV空間方向圖，如圖2所示。本文所有分析計算案例均將右旋圓極化定義為主極化，左旋圓極化定義為交叉極化。

圖1 線極化偶極子陣列仿真模型圖

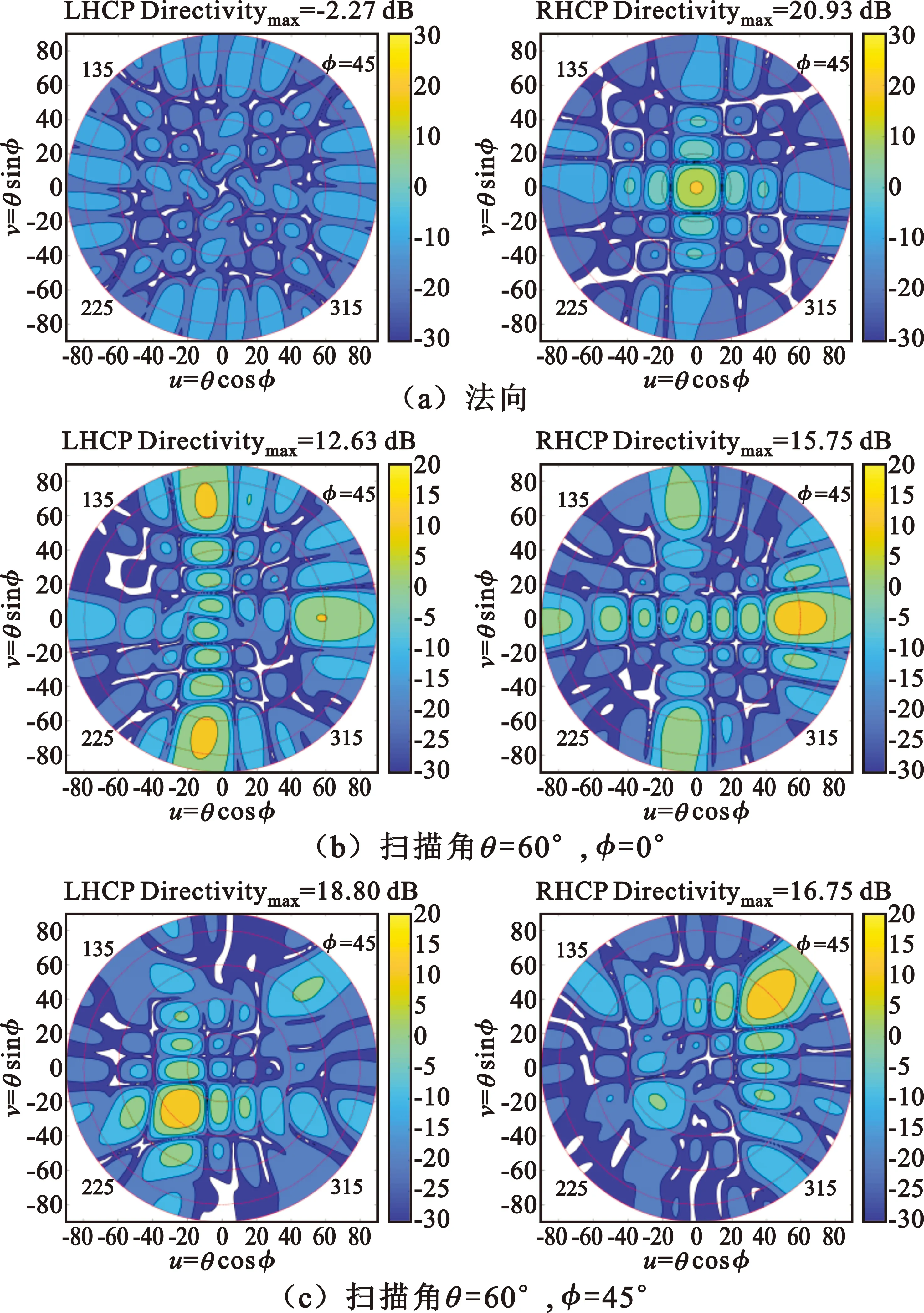
圖2 線極化偶極子陣列仿真增益(dB)方向圖

從圖2可看出，法向的交叉極化抑制高；沿基線掃描至θ=60°|φ=0°，交叉極化柵瓣出現在θ=60°|φ=0°、θ=65°|φ=100°、θ=65°|φ=260°三個方向附近，交叉極化方向性高時主極化方向性降低；沿對角線掃描至θ=60°|φ=45°，交叉極化柵瓣出現在θ=30°|φ=225°附近，電平比主極化峰值還高。

圖3所示的仿真模型中，單元排布方式、陣列規模、饋電方式等均與圖1的模型相同，僅將天線單元替換為圓極化十字偶極子天線。該陣列仿真結果如圖4所示。

圖3 圓極化偶極子陣列仿真模型圖

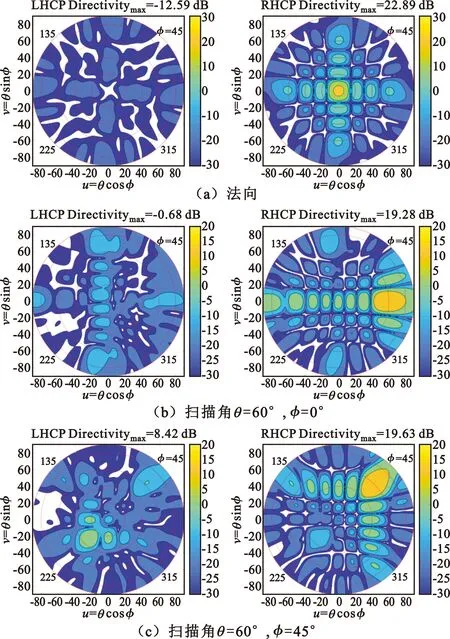
圖4 圓極化偶極子陣列仿真增益(dB)方向圖

對比以上兩種圓極化合成陣列的算例，線極化單元合成比圓極化單元合成增益約低3 dB，交叉極化抑制低10 dB。所以用線極化單元合成左右旋可變的陣列，是一種效能較差的設計，應盡量避免采用，如必須采用則需要對交叉極化抑制和陣列增益做重點設計。

1.2 順序旋轉陣列交叉極化陣因子

在面對上百元的毫米波陣列式，全尺寸三維電磁場仿真計算量過大，效率低下。本文提出一種將單元極化特性與順序旋轉陣列交叉極化特性分離的方法，從順序旋轉的相位分布去考察交叉極化特性，能準確快速地評估旋轉方式的優劣。

定義平面相控陣單元的指向控制項[6](Array Manipulation，AM)為

AMmn(θ,φ)=ejk(xmnsin θcos φ+ymnsin θsin φ-xmnsin θbcos φb-ymnsin θbsin φb)。

(1)

式中：k是自由空間波數，xmn、ymn是陣元坐標，m、n為平面陣沿x、y向的編號，θ、φ是觀測角，θb、φb是指向角。則平面陣列的右旋圓極化電場方向圖公式為

(2)

式中：ERemn(θ,φ)是單元右旋圓極化電場，ΦRnm是合成右旋圓極化時激勵電流中的旋轉補償相位。

將式(2)改寫為

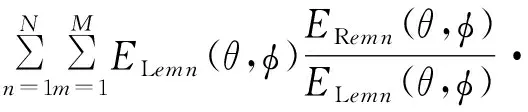
[AMmn(θ,φ)e-jΦRnmejΦLmn]e-jΦLmn。

(3)

式中：ELemn(θ,φ)是單元左旋圓極化電場,ΦLmn是合成左旋圓極化時激勵電流中的旋轉補償相位。則上式具有左旋圓極化電場方向圖的形式，可理解為右旋陣列產生的寄生左旋分量。將式(2)、(3)中與單元特性相關的項(單元方向圖、旋轉相位)去掉，僅保留純陣列因子，得到下面兩個陣因子。

定義右旋(主極化)陣因子為

(4)

寄生左旋(交叉極化)陣因子為

(5)

主極化(右旋)與寄生交叉極化(左旋)的饋電相位相差為ΦR-ΦL，二維陣列全部單元的相位差可匯總為矩陣形式。

未采用順序旋轉的圓極化陣列，其主極化和交叉極化陣因子相同，所以全陣的圓極化極化特性僅由陣中單元極化特性決定。另外，如在饋電時將旋轉補償相位反向，將造成陣列極化與單元極化相反，不能合成主波束，在工程中應特別注意。

將這種子陣平移擴展至大陣，以8×8陣列為例，旋轉相位的差值矩陣為

(6)

由式(6)可見，交叉極化這一寄生的相位分布在陣口徑中形成相位振蕩，將對交叉極化產生影響，在大俯仰角度掃描，特別是沿對角線掃描時更為明顯。相位振蕩引起交叉極化出現柵瓣，導致主極化增益下降。圖5是UV空間陣因子方向圖，與圖2對比可見主極化及交叉極化的主瓣、柵瓣預計準確。

僅從陣因子方向圖可見，正方形陣列網絡2×2子陣順序旋轉法向的交叉極化最優，但掃描至大角度時出現交叉極化柵瓣。

陣因子仿真與三維電磁場全波仿真相比，主瓣、柵瓣位置重合，電平相當，只是未能體現出在大角度掃描時由于單元方向圖極化抑制不足而在主極化主瓣指向形成的交叉極化高電平副瓣。下面對這種現象進行解釋。

根據電磁波極化理論，右旋圓極化波的極化比(Polarization Ratio，PR)定義[7]如式(7)，如果右旋為主極化，則PR>>1。

(7)

從上式可得到結論：圓極化波的軸比越好(即|Ex|與|Ey|越接近)，則極化比越高，反之亦然。

由于陣因子本身不具有極化特性，全陣面的交叉極化是通過陣元的交叉極化特性來轉換的。根據式(7)，左旋分量引起的右旋分量為EL×PR。同理,右旋分量引起的左旋分類為ER×PR。

將式(2)改寫，增加單元的交叉極化分量，得到以下兩個式子，分別為右旋圓極化電場及寄生左旋圓極化電場。

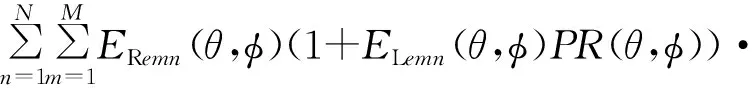
AMmn(θ,φ)e-jΦRnm，

(8)

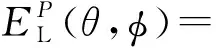
AMmn(θ,φ)e-jΦRnm。

(9)

運用式(8)、(9)可將交叉極化分量耦合到主極化中，也可將主極化分量耦合到交叉極化中。由于將線極化天線電場分解為左旋和右旋圓極化，得到的圓極化比非常低(接近1)，所以用線極化單元合成的順序旋轉陣列左右旋分量相互耦合很強。這就解釋了圖2三維電磁場仿真掃描狀態結果中，無論主極化或交叉極化，其主瓣和柵瓣均在對應的極化中相同的方向產生副瓣。

1.3 正方形網格2×2子陣二階順序旋轉分析

我們設計了另一種旋轉方式，2×2子陣間再疊加順序旋轉相位擴展，稱為2×2子陣二階順序旋轉。以8×8陣列為例，將子陣順序旋轉擴展至大陣時，子陣以90°的角度增量整體順序旋轉。

右旋圓極化的相位補償矩陣為

(10)

左旋的相位補償矩陣為ΦL=-ΦR，全陣的旋轉相位的差值矩陣為

(11)

交叉極化陣因子方向圖如圖6所示。

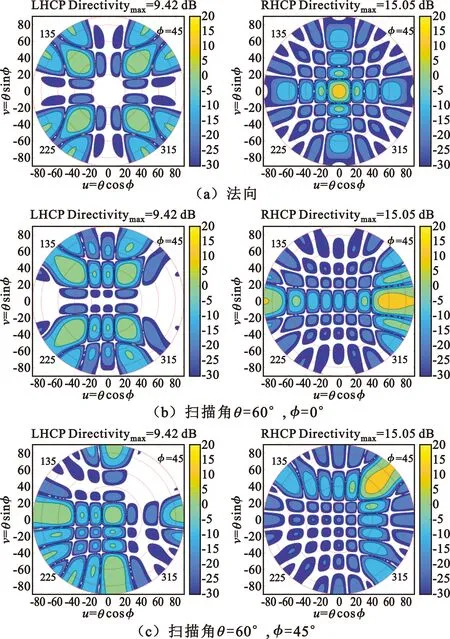
圖6 2×2子陣二階順序旋轉陣列的陣因子仿真增益(dB)方向圖

從圖6的陣因子方向圖可得到以下結論：法向交叉極化比傳統的2×2子陣順序旋轉方式略高，但大角度掃描時交叉極化柵瓣電平得到明顯抑制。分析其機理，我們認為這種順序旋轉陣列的擴展方式將交叉極化柵瓣相位分布周期提高一倍，交叉極化柵瓣分裂為4瓣(方位、俯仰各一次分裂)，從而將交叉極化柵瓣峰值電平降低6 dB。

由于正方形2×2子陣旋轉方式的周期性，正方形網格以90°為增量旋轉只有少數幾種規則的方式。要進一步抑制柵瓣，可以給每個單元附加隨機的旋轉角度，利用優化算法搜索一組最佳值[8-9]。

下面給出陣列實物模型的HFSS仿真結果，驗證順序旋轉方式設計的有效性。圖7是采用2×2子陣二階順序旋轉的陣列模型，圖8是線極化單元陣列三維電磁場仿真結果，圖9是圓極化單元陣列三維電磁場仿真結果。

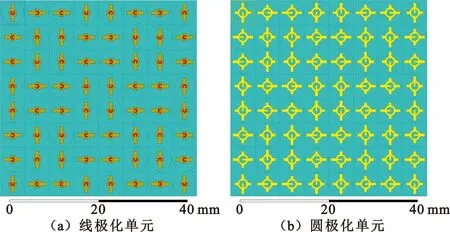
圖7 2×2子陣二階順序旋轉陣列模型圖

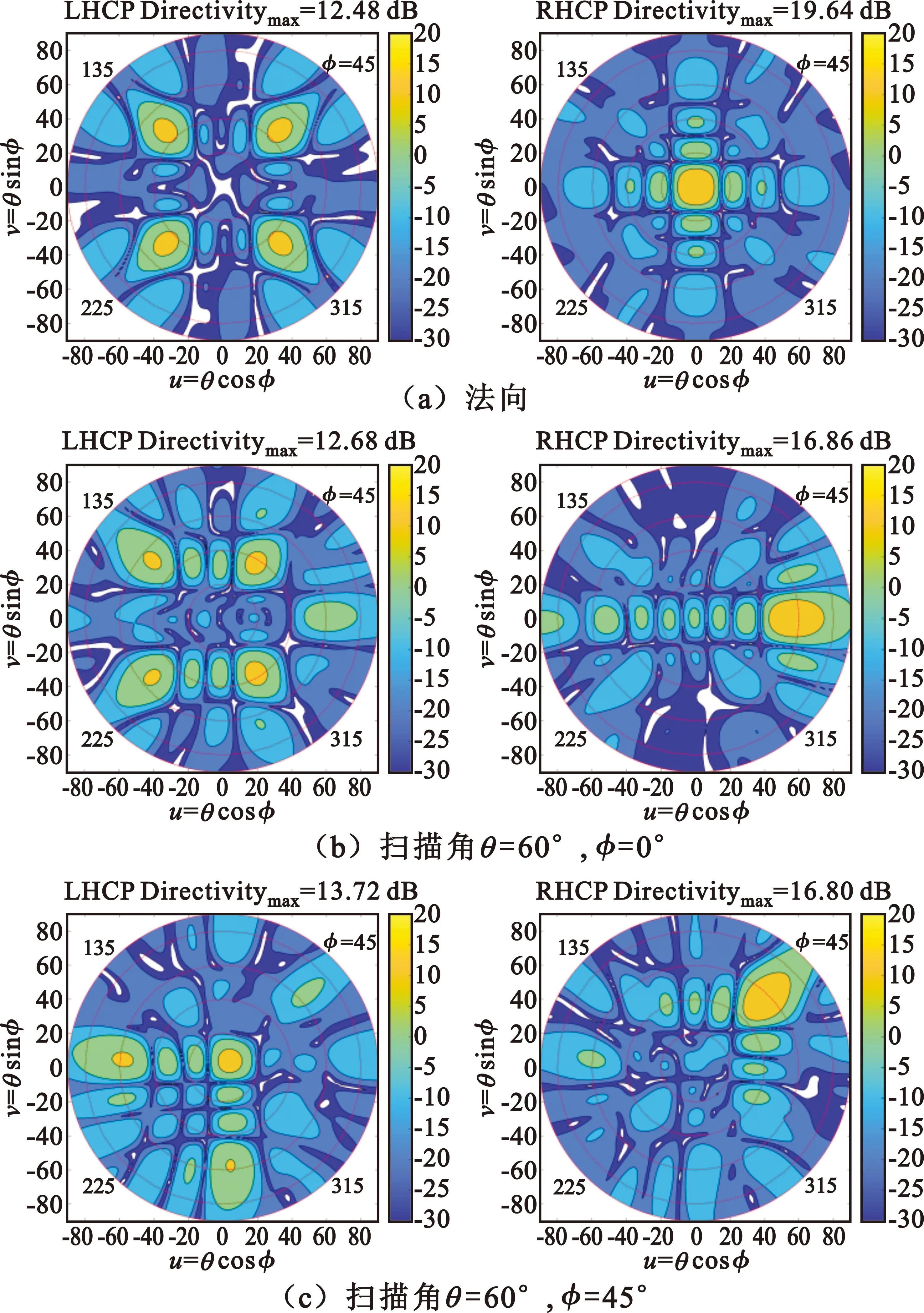
圖8 線極化單元2×2子陣二階順序旋轉陣列仿真增益(dB)方向圖

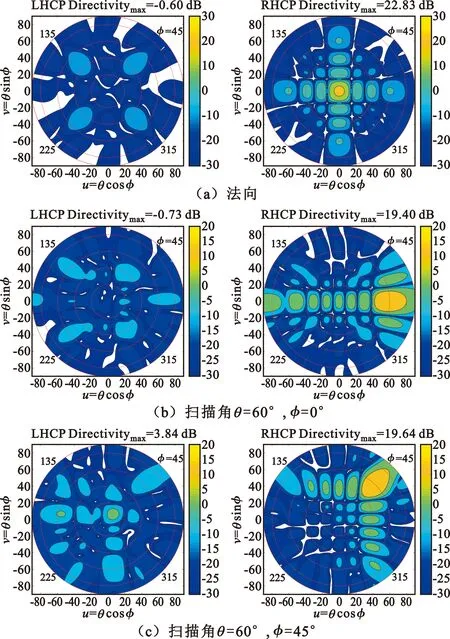
圖9 圓極化單元2×2子陣二階順序旋轉陣列仿真增益(dB)方向圖

從圖8和圖9的三維電磁場仿真結果可看出，二階順序旋轉對交叉極化的抑制度比常規的順序旋轉提高6 dB，與本節利用交叉極化陣因子和旋轉相位差值矩陣理論分析預計值符合。

1.4 正方形網格陣列全局順序旋轉分析

以上兩種以子陣為單元的旋轉方式均具有較強的周期性，使交叉極化出現柵瓣。

根據徑向線圓極化天線的饋電原理，我們設計了一種全陣面旋轉的饋電方式，每個單元的旋轉角度為其相對于陣列中心的相位角。直觀上這種旋轉方式可能具有較好的交叉極化。

全局旋轉陣列單元旋向示意圖如圖10所示，該陣列形成右旋圓極化。

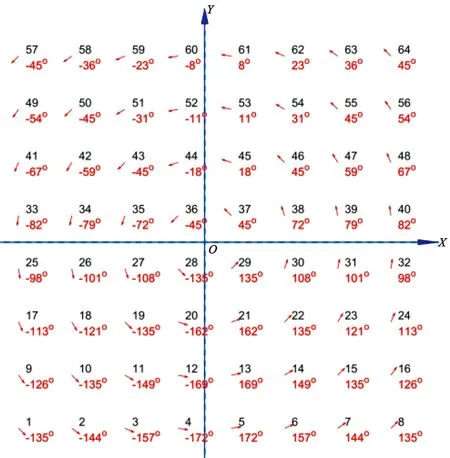
圖10 全局旋轉陣列示意圖

形成右旋的單元旋轉相位補償值矩陣為

(12)

左旋的相位補償矩陣為ΦL=-ΦR，而差值矩陣如式(13)所示：

(13)

由式(13)可見，旋轉相位差矩陣ΦR-ΦL具有以陣列中心呈反旋轉對稱的特性，但沿周向的相位變化無明顯突變，類似于圓口徑貝利斯差波束口徑場相位分布[10]。所以可以判定采用這種旋向的圓極化陣列，其交叉極化的主瓣與主極化主瓣同步移動，但波束中心具有圓形的零陷(即差波束)，其最大值出現在主極化第一零點附近，形成一個圍繞主極化主瓣的環形區域。由于篇幅所限，僅列出掃描θ=60°、φ=45°的陣因子方向圖。

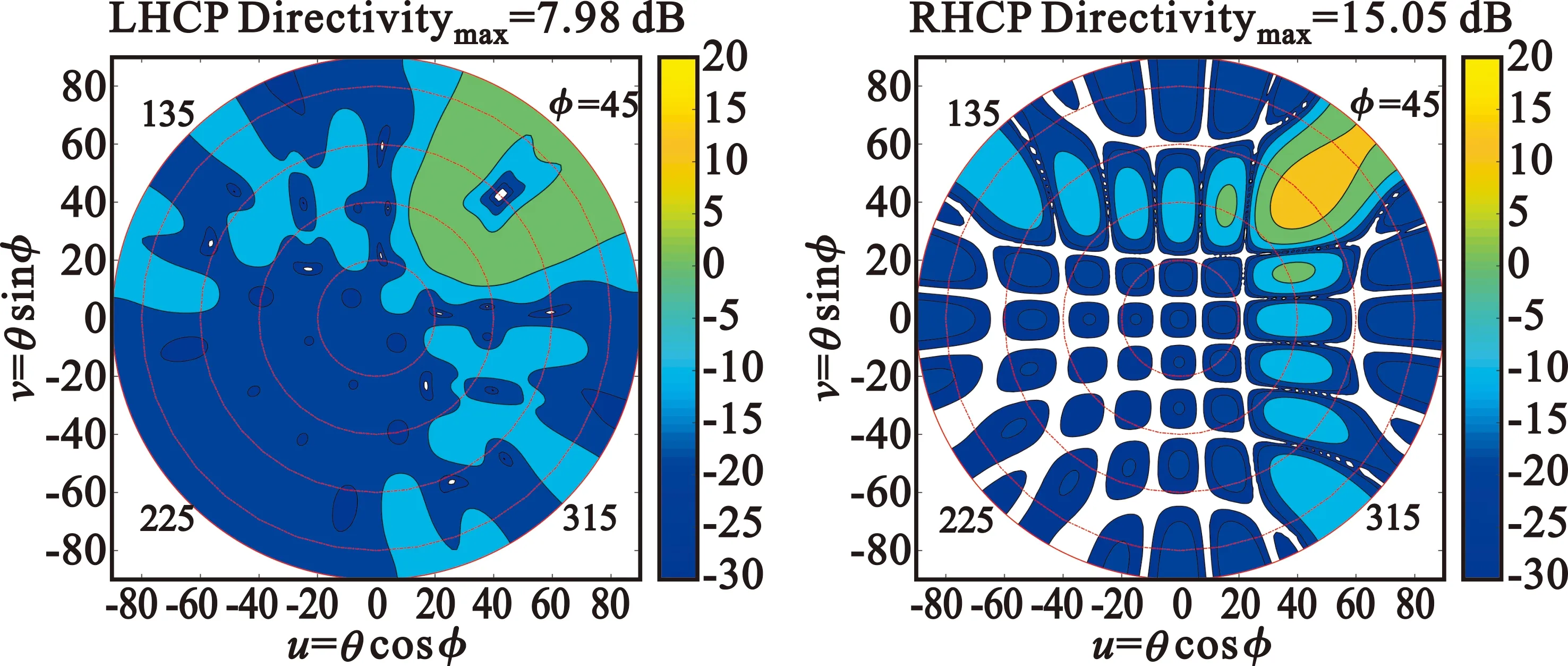
圖11 全局旋轉陣列陣因子仿真增益(dB)方向圖

由于每個單元的旋轉方向不同，這種陣面在實際應用中面臨天線結構設計、饋電轉接等問題，增加了設計復雜度，所以工程中常采用簡化的全局旋轉方案，即1/4陣面整體順序旋轉。圖12為這種順序旋轉的示意圖，式(14)是旋轉相位差值矩陣。

圖12 1/4陣列順序旋轉示意圖

(14)

由式(14)旋轉相位差值矩陣可看出，其具有俯仰、方位二維可分離差波束的口徑相位分布的特征。

從圖13(掃描θ=60°、φ=45°的陣因子方向圖)可看出，1/4陣列順序旋轉相比于全陣順序旋轉，交叉極化的主瓣分裂為4瓣，與俯仰、方位二維可分離差波束形狀一致，交叉極化峰值電平略高。

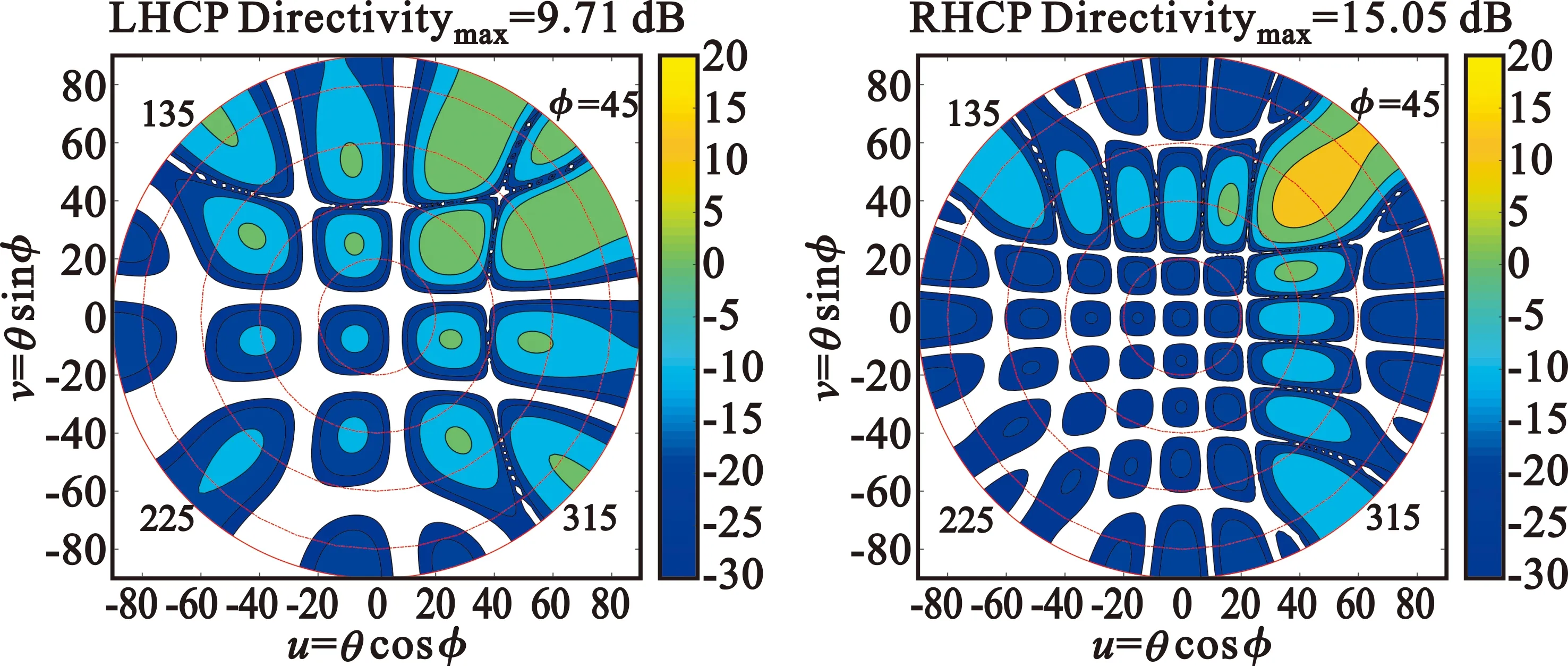
圖13 1/4陣列順序旋轉陣因子仿真增益(dB)方向圖

1.5 三角形陣列順序旋轉分析

三角形陣列在相同口徑增益的條件下，單元數比正方形陣列少13%[11]，在大規模相控陣中常用。由于三角形網格的主副基線不正交，所以順序旋轉圓極化合成的方式更多，設計更靈活。圖14列出了四種三角形陣列的旋轉布陣示意。

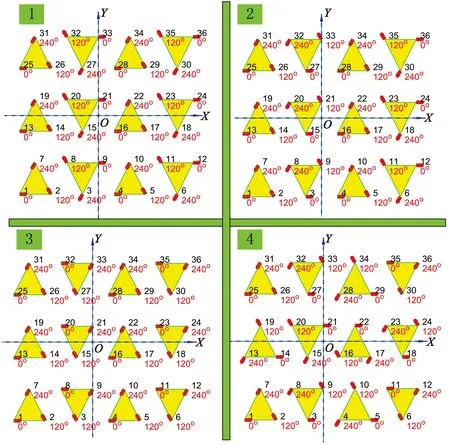
圖14 四種三角形順序旋轉陣列示意圖

運用1.2節的公式，對以上四種三角形順序旋轉陣列的主極化、交叉極化進行計算，不再用圖形展示，將主極化、交叉極化的主瓣及副瓣峰值的位置及電平列表，如表1所示。

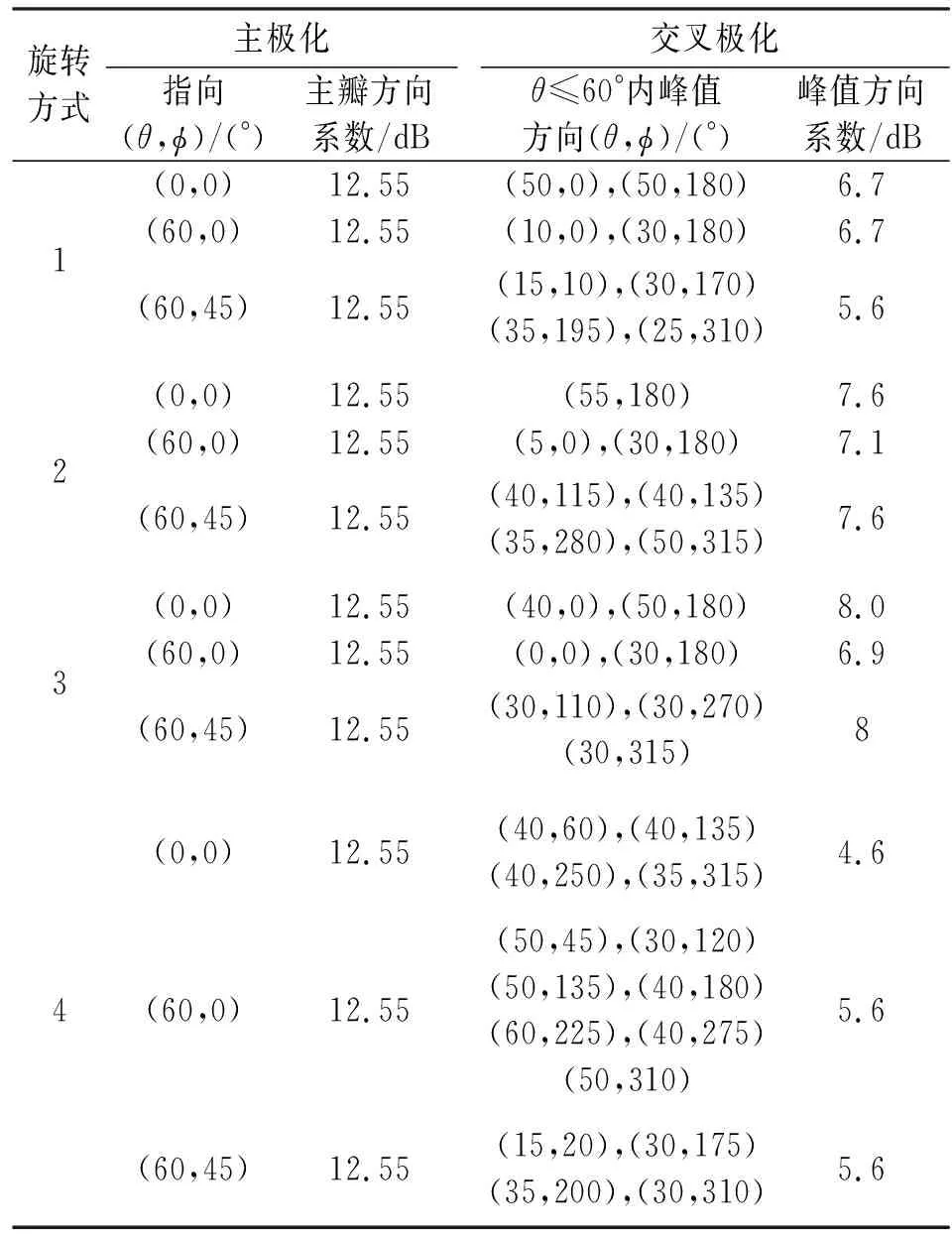
表1 三角形順序旋轉陣列指標統計

總的來講，三角形陣列的周期性比正方形陣列差，排列更無序，所以交叉極化柵瓣被分散，柵瓣電平最大值較低。在設計由線極化單元構成的左右旋可調陣列時，由于無可避免地存在交叉極化柵瓣，使用三角形陣列能實現更高的交叉極化抑制。圖15所示為工作在 19.5～23.5 GHz 的極化旋向可變的衛星通信相控陣原理樣機照片。該樣機采用三角形布陣，并利用遺傳算法對陣元旋向優化，全掃描空間內的交叉極化比均保持在12 dB以上。圖 16 為使用 NSI 天線近場測試系統對原理樣機進行測試的方向圖(掃描角θ=60°,φ=45°)，測試交叉極化比為10.5 dB。

圖15 可變極化旋向相控陣原理樣機

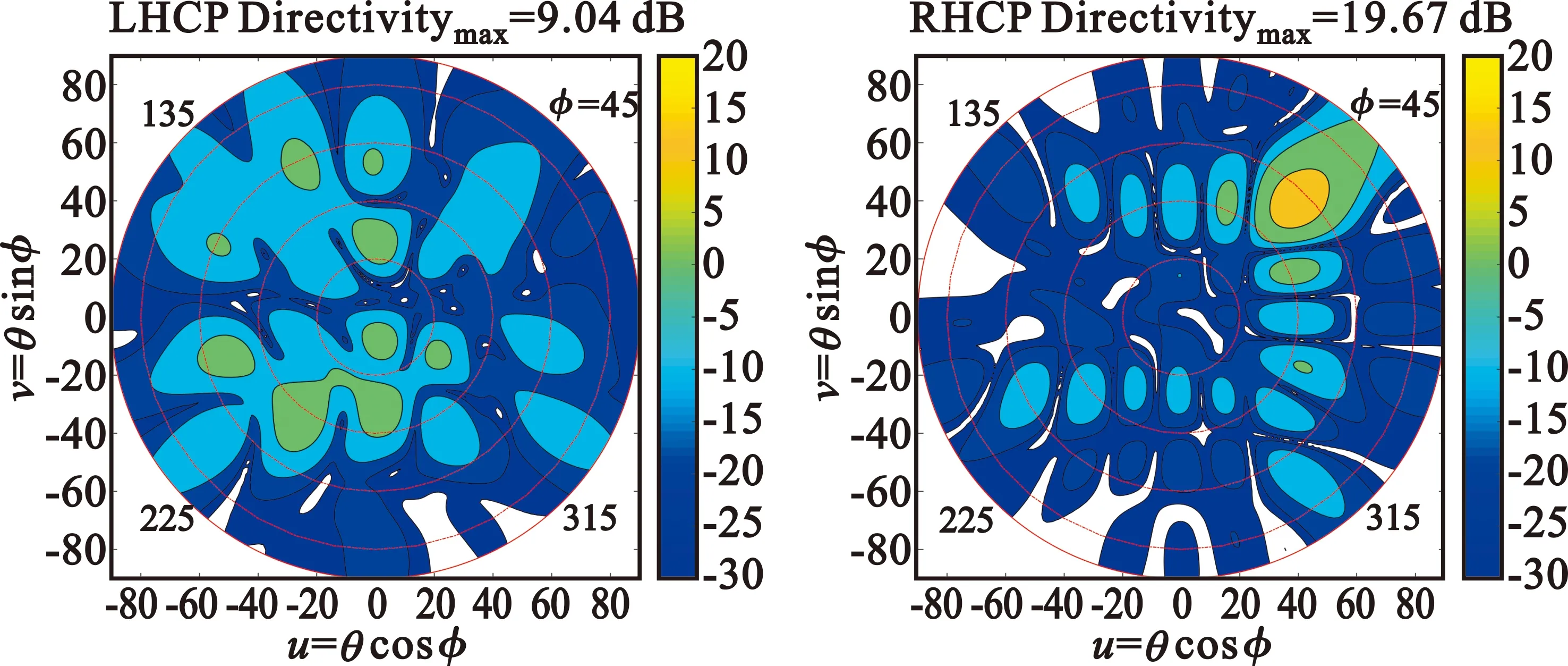
圖16 可變極化旋向相控陣測試增益(dB)方向圖

2 陣列單元圓極化特性

根據以上理論分析，為了使圓極化陣列達到最大的交叉極化抑制，除了抑制陣因子的寄身交叉極化以外，陣元也應具有寬角范圍高極化純度特性。在Ku以下的頻段，相控陣單元間距在厘米量級，陣元的加工精度高，可以采用多饋點微帶天線實現寬角范圍內高極化純度的單元方向圖。

在毫米波頻段由于加工工藝限制，常采用單饋點微帶和金屬偶極子作為陣元。在陣列環境中單元的寬角交叉極化惡化，旋轉對稱性差。更為嚴重的是由于陣中強互耦效應，圓極化單元的駐波和極化特性會發生較大改變，軸比可能惡化至10 dB以上，接近于線極化，導致陣列的交叉極化分量抬高。

天線單元的輻射方向圖可由其電流分布或閉合曲面的口徑場積分求得。由于天線的輻射結構越來越復雜，解析公式求解矢量場變得非常困難。依靠計算電磁學的發展，多種基于有限元、有限差分、積分方法的商業電磁場仿真軟件廣泛應用在工程中，達到了極高的精度。圖17是常用圓極化陣列天線單元模型，圖18～20列出了幾種有源相控陣常用的圓極化陣元的極化特性，主要考察全覆蓋角域的軸比和極化比。

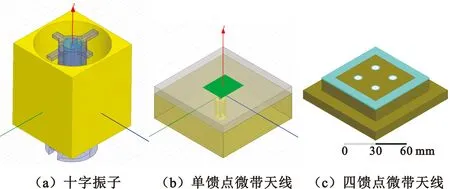
圖17 常用圓極化陣列天線單元模型圖

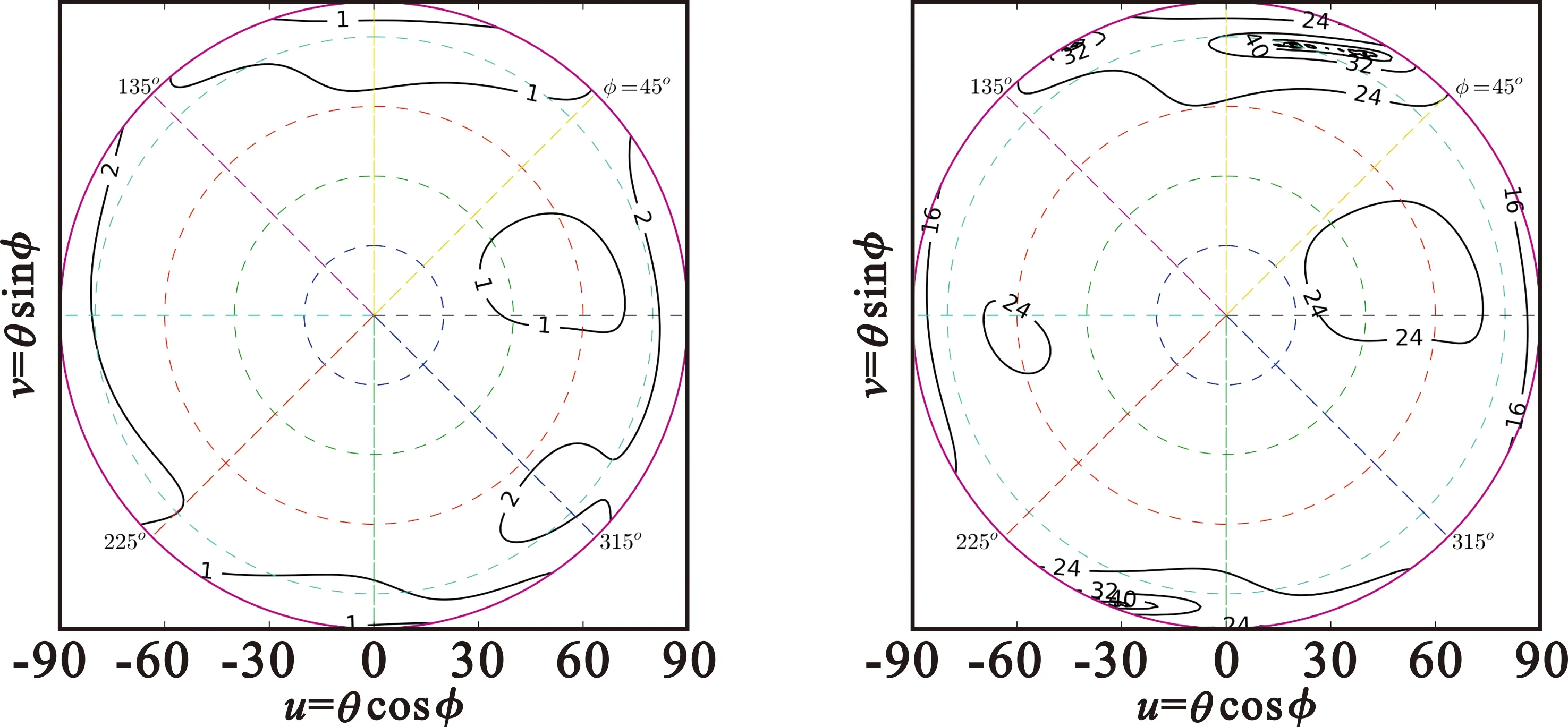
圖18 十字振子天線軸比與極化比(dB)

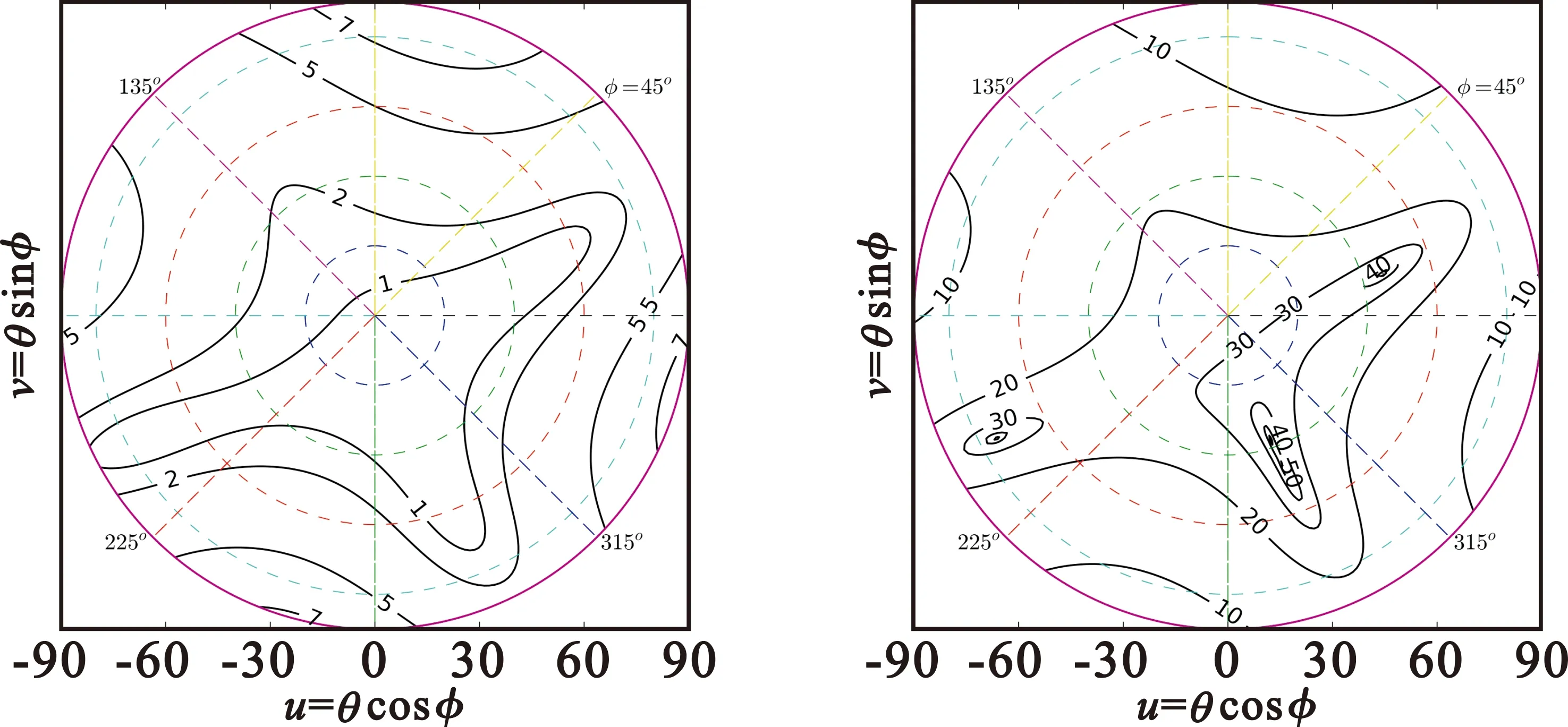
圖19 微帶天線軸比與極化比(dB)

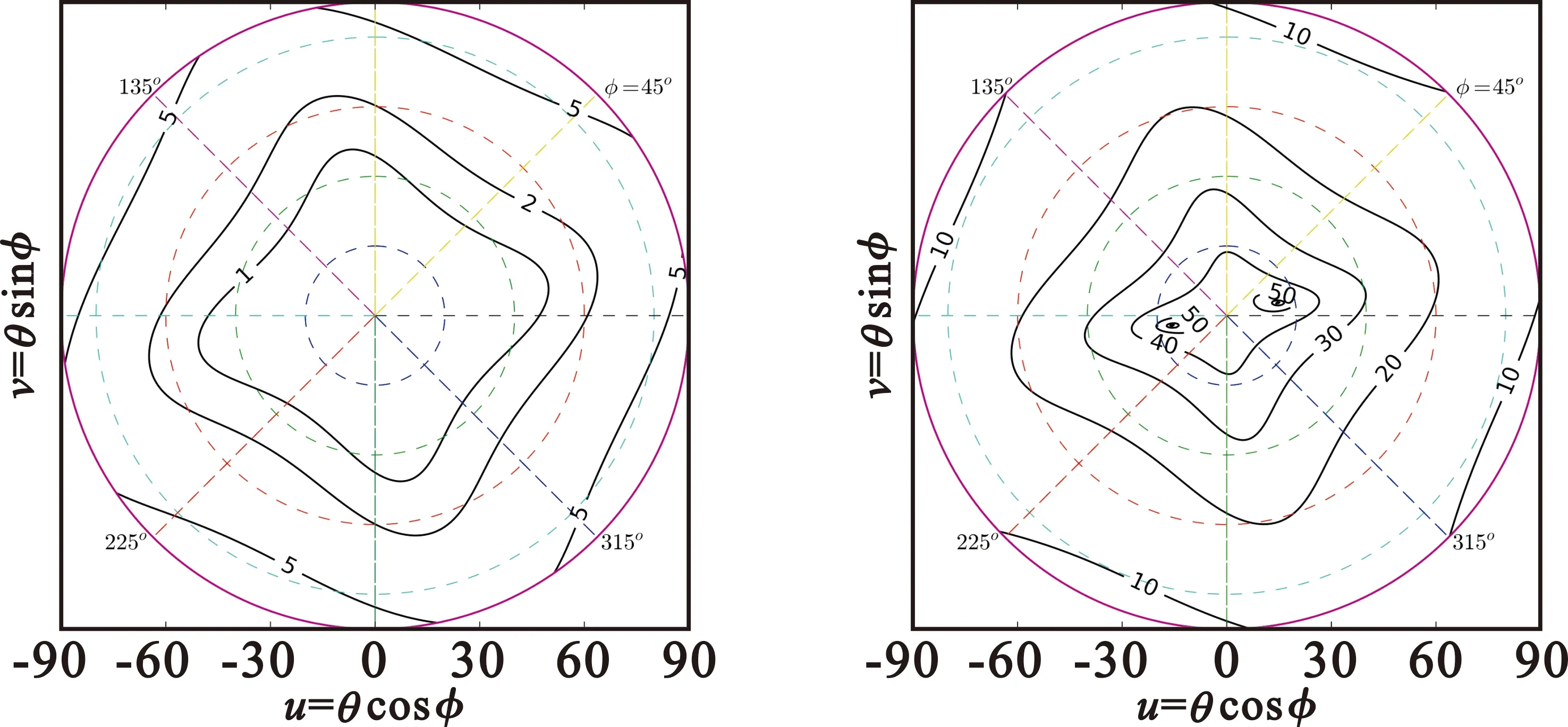
圖20 四饋點微帶天線軸比與極化比(dB)

由圖18～20可見，結構對稱性好、陣元間隔離度高的帶腔十字振子、四饋點微帶的軸比和極化比特性優良，而未做隔離設計的微帶天線軸比和極化比特性較差。

3 結 論

本文通過分析順序旋轉圓極化陣列的方向圖公式，推導出寄生交叉極化陣因子。利用這一簡便的表達式，對正方形、三角形陣列的順序旋轉方式進行了全面的研究。本文還定義了旋轉相位差值矩陣，基于這一描述順序旋轉陣列口徑相位分布的參數，可以直觀地評估順序旋轉方式的交叉極化抑制效果。本文詳細分析了如二階順序旋轉、全局旋轉等幾種能使正方形網格陣列交叉極化抑制達到最佳的旋轉方式。對于三角形陣或無序網格陣列，可采用本文的交叉極化陣因子，利用數值算法對每個單元旋轉方向進行優化設計。由于優化過程中未帶單元的極化特性，這種算法的計算量大幅減小，非常適用于大規模圓極化相控陣天線設計中的寬角域交叉極化特性的快速高效評估。