用于巡航導彈突防航跡規劃的改進深度強化學習算法

馬子杰，高 杰，武沛羽，謝擁軍

（北京航空航天大學 電子信息工程學院，北京 100191）

0 引言

巡航導彈是一種能機動發射、命中精度高、隱蔽性強、機動性能強的戰術打擊武器，但近年來由海陸空防御武器整合得到的體系化信息化反導防御系統態勢感知能力和區域拒止能力都得到了極大的提升，巡航導彈的戰場生存能力受到威脅，提升巡航導彈規避動態威脅的能力成為其能否成功打擊目標的關鍵[1-3]。傳統的巡航導彈航跡規劃方法中將雷達威脅建模為一個靜態的雷達檢測區域，這難以適應對決策實時性要求較高的動態戰場環境，而且其缺乏探索先驗知識以外的突防策略的能力，需要研究能應對動態對抗的巡航導彈智能航跡規劃算法。

深度強化學習是人工智能領域新的研究熱點[4-6]。隨著深度強化學習研究的深入，其開始被應用于武器裝備智能突防，文獻[7]利用深度強化學習提出了一種新的空空導彈制導律，提高了打擊目標的能力。文獻[8]針對目標、打擊導彈、攔截導彈作戰問題，探究了是否發射攔截導彈、攔截導彈的最佳發射時間和發射后的最佳導引律。文獻[9]利用深度價值網絡算法探究了靜態預警威脅下的無人機航跡規劃問題，提升了航跡規劃的時間。文獻[10]將雷達威脅建模為一個靜態的雷達檢測區域，在二維平面探究了巡飛彈動態突防控制決策問題，提高了巡飛彈的自主突防能力。

綜上所述，目前巡航導彈智能突防研究中針對預警雷達的威脅建模都屬于靜態建模，其設定預警機威脅區域固定，而實際戰場環境中預警機是動態的，因而其威脅區域也是動態變化的。因此，本文提出了兩點改進：（1）對預警機威脅進行動態建模，給出了預警機雷達探測概率的預測公式；（2）使用深度確定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法訓練時引入了時序相關的奧恩斯坦-烏倫貝克隨機過程作為探索噪聲，解決了收斂難度加大的問題，進而縮短了算法的訓練時間。

1 DDPG 算法及其改進

DDPG[11-13]是深度強化學習應用于連續控制強化學習領域的一種重要算法，將確定性策略梯度算法與Actor-Critic 框架相結合，提出了一個任務無關的模型，并可以使用相同的參數解決眾多任務不同的連續控制問題。DDPG 采取經驗回放機制，通過目標網絡的參數不斷與原網絡的參數加權平均進行訓練，以避免振蕩。深度確定性策略梯度算法流程如下：

輸入：環境；

輸出：最優策略的估計；

參數：學習率α（w）、α（θ）、折扣因子γ、控制回合數和回合內步數的參數、目標網絡學習率α目標。

（1） 初始化網絡參數：θ←任意值，θ目標←θ，w←任意值，w目標←w。

（2） For episode=1，M do（M 為仿真最大回合數）

（3） 用對π（S；θ）加擾動進而確定動作A

（4） 執行動作A，觀測到收益R 和下一狀態S′

（5） 將經驗（S，A，R，S′）儲存在經儲存空間D

（6） For t=1，T do（T 為仿真終止時間）

（7） 從存儲空間D 采樣出一批經驗B

（8） 為經驗估計回報U←R+γq（S′，π（S′；θ目標）；w目標）

1.1 DDPG 算法求解流程

DDPG 算法的網絡結構為Actor-Critic 網絡結構，其中Actor 網絡輸入狀態，輸出動作，Critic 網絡輸入狀態和動作，輸出在這一狀態下采取這個動作的評估Q 值，其示意圖如圖1 所示。由于巡航導彈、目標和預警機的狀態動作信息是一個在時間上連續的序列，因此由狀態構成的樣本之間并不具備獨立性，只使用單個神經網絡結構學習過程很不穩定。為解決這個問題，DDPG 算法引入了經驗回放機制，引入目標Actor 網絡和目標Critic 網絡，與現實網絡獨立訓練。首先現實Actor 網絡與環境進行交互訓練，得到狀態S、動作a、獎勵r、下一時刻狀態S′，將這4 個數據放入經驗池中，得到一定的樣本空間后，現實Critic 網絡從經驗池中提取樣本進行訓練得到Q 值；目標網絡也進行同樣的訓練，每間隔一定時間就利用現實網絡參數更新目標網絡。訓練完成后可以通過Actor 網絡得到高維的具體動作，可解決連續動作空間學習問題。其求解流程如圖2 所示。

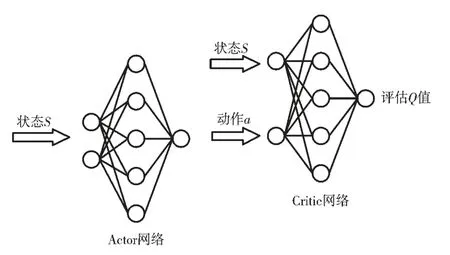
圖1 Actor-Critic 網絡結構

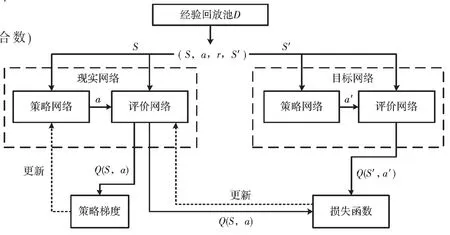
圖2 DDPG 算法流程圖[10]

1.2 DDPG 算法的改進

1.2.1 時序相關的探索噪聲

傳統的DDPG 算法中的探索噪聲為高斯噪聲，其在時序上不相關，對時序相關的問題探索能力差，探索時間長；導彈突防過程屬于慣性過程，引入時序相關的奧恩斯坦-烏倫貝克隨機過程可以提高在慣性系統中的控制任務的探索效率，使訓練更快收斂。奧恩斯坦-烏倫貝克過程滿足的微分方程為：

其中，xt為過程刻畫的量；θ為比例系數；μ是xt的均值；Wt為維納過程，是一種隨機噪聲；σ 是隨機噪聲的權重。

1.2.2 動態預警威脅

預警機是一種裝有遠距離搜索雷達、數據處理、敵我識別以及通信導航、指揮控制、電子對抗等完善的電子設備，用于搜索、監視與跟蹤空中和海上目標并指揮、引導己方飛機執行作戰任務的作戰支援飛機，起到活動雷達站和空中指揮中心的作用，是現代戰爭中重要的武器裝備。DDPG 算法應用于突防策略研究時，一般將預警機雷達威脅簡化為一個靜態的禁飛區，但這樣無法反映真實作戰場景下巡航導彈遇到的動態預警威脅，因此在解決巡航導彈突防航跡規劃問題時，需要在DDPG 算法中引入預警機雷達動態探測概率預測公式。

E2-D 預警機的雷達在一定的虛警概率下，一次掃描對目標的發現概率為[14]：

式中：

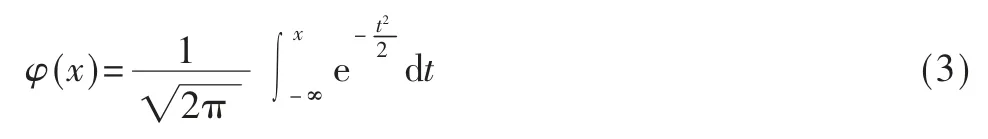
其中，no為一次掃描脈沖積累數，yo為虛警時的檢測門限，S/N 為信噪比。

對其曲線進行擬合可得預警雷達探測瞬時概率與目標的雷達散射截面積值σ 和目標與雷達的R的計算公式為：

其中，R的單位為km，σ的單位為m2；c1與c2和雷達的工作模式和場景有關，本文分別取為1.5和1.5×10-8.5。

2 巡航導彈突防決策模型

巡航導彈突防過程為一個馬爾科夫決策過程（Markov Decision Process，MDP），需要對導彈運動模型、狀態空間、動作空間、獎勵函數進行建模。

2.1 導彈運動模型

可以對突防過程的彈道進行簡化：導彈和預警機均可視為質點，巡航導彈采用3自由度質點運動。

2.2 狀態空間設計

由于對抗雙方均設為質點，可以將巡航導彈、目標、預警機的質心位置ot、彈目質心位置的距離lt以及航向角φt作為狀態空間，即狀態空間為st=[ot，lt，φt]。

2.3 動作空間設計

巡航導彈處在一個連續的動作空間，其動作空間設為巡航導彈在x、y、z 3 個方向的速度分量，即vx、vy、vz。

2.4 獎勵函數設計

2.4.1 導彈成功擊中目標獎勵

巡航導彈采取突防策略的主要目的是在避開預警威脅的情況下，成功擊中目標。其獎勵函數為：

2.4.2 導彈和目標相對距離獎勵

導彈可目標的距離越近，導彈擊中目標的可能性越大，其獎勵函數為：

其中，lt為導彈與目標當回合的距離。

2.4.3 導彈速度和彈目連線夾角獎勵

導彈速度和彈目連線夾角即為視線角，視線角越小，巡航導彈擊中目標的可能性越大，其獎勵函數為：

其中，φt為導彈與目標當回合的視線角。

2.4.4 視線角變化率獎勵

視線角變化率獎勵的具體形式為：

其中，φt-1為導彈與目標上一回合的視角。

2.4.5 探測概率降低獎勵

其中，Pd為雷達探測概率，k 為比例系數。

綜合考慮上述5 種獎勵模型，每回合巡航導彈的動作獎勵為：

訓練完成后的總獎勵為：

3 仿真結果與分析

3.1 仿真場景及武器性能參數

仿真場景主要對巡航導彈、攻擊目標、預警機的位置、機動參數和機動范圍進行設置。作戰場景如圖3 所示，主要為巡航導彈、目標和預警機的空間位置關系。預警機在7 500 m 高度以“跑道形”巡邏線探測巡航導彈，直邊長度為70 km，弧線半徑為15 km，航線中心點坐標為東經119.5°、北緯20°、海拔7 500 m。巡航彈目標為位于東經120°、北緯20°、海拔15 m的宙斯盾艦船，巡航導彈的發射點位于東經117.5°、北緯20°、海拔15 m。其中巡航導彈的最大巡航速度為300 m/s，目標的最大速度為200 m/s；當巡航導彈和目標的相對距離小于0.05 km時假定巡航導彈擊中目標。

圖3 巡航導彈突防典型作戰場景

3.2 軟硬件環境及參數設置

仿真的軟件環境為：Windows 10、Python3.7以及TensorFlow 架構，硬件環境為GTX2060 和64 GB DDR4 內存。Actor、Critic 神經網絡結構均采用2 層隱藏層的全連接神經網絡，隱藏單元數為256 和32；超參數設置如下：學習率為0.000 1，折扣因子為0.95，目標網絡更新系數為0.005，經驗回放池容量為10 000。

3.3 仿真結果分析

分別使用傳統DDPG 算法和改進DDPG 算法對巡航導彈應對動態預警威脅突防進行訓練，其每回合獎勵值曲線如圖4 所示，數據對比如表1 所示。

圖4 算法改進前后不同訓練回合數下的獎勵值

表1 算法改進前后數據對比

改進后的DDPG 算法由于其探索噪聲時序相關，探索能力更高，收斂速度更快，相較于傳統的算法模型訓練達到穩定時間縮短了一半，訓練收斂后改進算法每回合探索步數更少，因而其穩定每回合獎勵值更低。訓練完成后模型能在1 s 內生成巡航導彈自主避開預警威脅打擊目標的機動軌跡指令。

圖5 為模型訓練完成后測試模型得到的一個攻防場景圖，其中預警機巡航軌跡為跑道型軌跡，目標直線航行，巡航導彈避開預警威脅后成功擊中目標。

圖5 典型作戰場景下訓練后攻防軌跡圖

4 結論

本文首先構建了巡航導彈突防時的典型作戰場景，給出了預警機雷達探測概率的預測公式；然后采用一種基于時序相關探索噪聲的改進DDPG 算法求解得到了巡航導彈快速智能突防算法。仿真實驗表明，在預警機雷達威脅下采用上述算法巡航導彈可以實現快速主動突防。該模型的訓練時間大約為30 min，訓練完成后可在1 s 內生成突防機動軌跡，遠遠超過傳統航跡規劃算法的速度；而且該算法具備良好的適應性和延展性，可用于廣泛的作戰場景中。