探究式學習
——冪級數在數據結構中的應用研究

張 瑜 騰 旭

（[1]麗江文化旅游學院 云南·麗江 674100；[2]云南省衡水實驗中學 云南·昆明 650100）

1 背景與意義

在信息科技高速發展時代，科學技術更新越來越快，任何人必須不斷地學習才能適應社會的需求，才能不被信息社會淘汰，因此每個人都需要一個有效學習方式，而探究式學習是一個主動獲取知識的有效學習方式。然而在實際教學中，部分教師對學生能力的發展不夠重視，仍然采取傳統教學方式，而傳統教學方式以教師講授，學生接受的方式，機械的記憶知識和儲存知識，忽略學生是學習的主體，不重視學生培養各種能力。探究式學習是學生在教師設置的情境中，在教師的指導下，以一種主動的態度去探索問題，進而獲得新知識的一種學習方式。學生通過參與探究活動，可以自主獲得知識與技能，同時發展探索精神，培養創新能力，提升綜合素質等。探究式學習教學方式能彌補傳統教學方式的不足，在提升學生綜合素質方面起到積極的促進作用。因此，如何在數學教學中進行探究式學習這一問題具有很高的研究價值。

2 探究式學習的內涵

探究一詞在《現代漢語詞典》解釋為探索研究；探究原因。《辭海》中探究指的是深入探討，反復研究。探究一詞的英文為“inquiry”，解釋為詢問；調查；問題；疑問；研究。美國人韋爾奇等人認為：“探究是人類尋求信息和理解的一般過程”。

美國國家科學教育標準給出探究的定義是：“探究是多層面的活動，包括觀察，提出問題；通過瀏覽書籍和其他信息資源發現什么是已經知道的結論，制定調查研究計劃；根據實驗證據對已有的結論做出評價；用工具收集、分析、解釋數據，提出解答，解釋和預測以及交流結果。探究要求確定假設，進行批判和邏輯的思考，并且考慮其他可以替代的解釋。”事實上這個定義給出了探究式學習的一般過程：觀察并提出問題——查閱資料并制定研究計劃—收集、分析、研究資料，并解決問題—質疑并多方尋求答案。但也并不是所有的探究式學習都要嚴格按這個過程執行。針對不同學科特點，探究式學習的步驟會有所不同。

任長松在《探究式學習—學生知識的自主構建》一書中認為：探究式學習是指學生圍繞一定的問題、文本或材料，在教師幫助和支持下，自主尋求或自主建構答案、意義、理解或信息的活動和過程。

徐學福在《探究學習的教學模式》一書中認為：“所謂探究學習是指學生在教師指導下，為獲得科學素養以類似科學探究的方式所開展的學習活動”。

張崇善認為探究式教學“指教學過程是在教師的啟發誘導下，以學生獨立自主學習和合作學習為前提，以現行教材為基本探究內容，以學生周圍世界和生活實際為參照對象，為學生提供充分自由表達、質疑、探究、討論問題的機會，學生通過個人、小組、集體等多種形式解難釋疑的嘗試活動，將自己所學知識應用于解決實際問題的一種教學形式。”

綜上所述，探究式學習是指在教師引導下，學生通過自主學習和小組討論方式，提出，分析和解決問題，總結，反思，交流學習成果等學習活動，以此獲得知識和能力的一種學習方式。

3 探究式學習的數學教學的基本步驟

所謂探究式學習的數學教學：就是將探究式的學習方式應用到數學教學的課堂上。在研究中，數學探究式學習是指將在數學的教學中創設一種問題研究的情境，讓學生獨立思考，觀察，分析，歸納，推理，計算等探究活動中，獲得數學的知識與技能，思維的培養，特別是獲得探索精神、獨立思考能力和創新思維的培養。探究式學習的數學教學是以問題為導向，引導學生獨立思考，自主探索問題，解決問題的方法，充分發揮學生的主體地位。

探究式學習的教學的基本步驟：

3.1 創設情境，提出問題

根據數學教學的內容，創設情境，創設情境時，對于大學數學課程，教師可能很難在學習生活中找到案例，因此教師可以聯系學生已有的知識來設置問題情境，或者聯系專業課中數學的一些應用，以此激發學生的學習興趣和提高學生的參與度。

3.2 抽象并提出假設，建立抽象數學概念或建立模型

創設出數學情境后，教師引導學生分析問題，弄清楚什么是已知條件，什么是未知問題，找出它們之間的關系，假設出已知量和未知量，抽象建立數學模型。

3.3 研究和驗證數學概念或模型

數學家建立數學模型后需要不斷的驗證和修改，最終才能得到比較理想的數學模型。學校教育中所給的數學模型是經過數學家認可的，往往不需要驗證的，教材中往往以定義，定理的方式給出，于是在建立數學模型后，為了熟悉數學模型，教師可以引導學生利用數學模型解決實際問題。

3.4 拓展應用，總結反思

把數學學習內容拓展到專業課中，讓學生看到學過的數學知識在專業課中的應用，以此激發學生學習的興趣，培養學生的創新思維和獨立思考能力。

4 關于冪級數的探究式學習的教學研究

級數是高等數學中一個重要的內容，在初等數學中已經知道，“有限個實數的相加”，其和一定是一個實數，而“無限個實數相加，”則其和是否存在，若存在和是多少呢？若不存在又如何呢？實際上，這就是級數研究的一個問題。

而冪級數是一類最簡單的函數項級數，從某種意義說它可以看成是多項式的推廣，冪級數在理論和實際上都有很多應用，如冪級數在計算機專業課數據結構中有重要的應用。

4.1 創設問題情境，展現冪級數在數據結構中應用

冪級數在數學結構中有重要的應用，如在數據結構的遞歸函數部分，冪級數可以證明Fibonacci數列的通項，而Fibonacci數列可以通過遞歸實現。冪級數還可以來證明二叉樹的計數問題。在課堂中展現這兩個問題，這樣讓學生看到冪級數在數據結構中應用，以此激發學生學習冪級數的積極性和參與度。

4.2 探究冪級數的概念及相關定理

課堂上教師引導學生探究關于三種的級數的異同。給學生充分時間討論和思考，引導學生分析對比三種級數的相同點與不同點。引導學生總結出相同點：級數都是無窮項的和，而不同點是數項級數的通向的變量是n，而函數項級數和冪級數中通項的變量是x，冪級數的每一項都是x的冪函數。

函數的冪集數的展開。

引導學生對比這兩個級數，得出結論：泰勒級數是函數一般的展開形式，麥克勞林級數是泰勒級數的特殊形式。

實際上，函數的冪級數的展開都是根據麥克勞林公式展開的。

4.3 拓展冪級數的應用

4.3.1 冪級數在計算Fibonacci數列的通項中的應用

Fibonacci數列是0,1,1,2,3,5,8,13,21,34,55,89,144,233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368，特別說明該數列：第1項是0，第2項是第一個1。這個數列從第3項開始，每一項都等于前兩項之和。

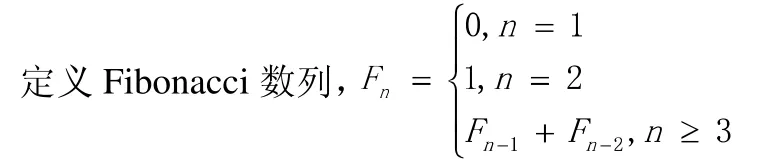
Fibonacci數列是數學中典型的遞歸問題，那么只要求出該數列的通項公式，那么可以用數據結構中遞歸函數實現它，Fibonacci數列是數據結構中典型的遞歸實例。下面探究該數列的通項公式，

根據Fibonacci segance,給出產生式（生成式）：

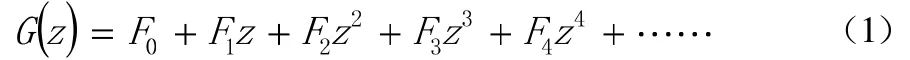
事實上，該式構造就是冪級數的應用，

求 Fibonacci數列通項公式和二叉樹的計數問題是數據結構中比較重要的問題，這兩個問題的解決用到冪級數中比較特殊的麥克老林級數的展開式，或者說用二項式的展開式。冪級數的學習是比較重要，因為它在專業課中有重要的應用。在高等數學中冪級數這部分的學習可以采用探究式學習的教學方式，并且引導學生探究式學習冪級數的定義后，引導學生探究式學習Fibonacci數列通項公式和二叉樹的計數問題，讓學生看到冪級數是在數據結構中的應用，這樣可以提高學生學習冪級數的積極性和主動性。

5 總結和展望

本文分析探究式學習的意義與內涵，探究式學習的教學方法可以培養學生獨立思考的能力和創新思維，在探究式學習的教學中如何提高學生的積極性和參與度，本文提出在創設情境時結合專業背景，并且在總結反思環節，結合專業應用進行拓展，以此提高探究式學習的教學中學生的積極性和參與度。本文以大學課程《高等數學》中的冪級數為例，并結合冪級數在計算機專業課程《數據結構》中的應用，采用探究式學習的教學法，探究冪級數的內容。本文在許多方面都有待研究，探究式學習的數學教學的相關理論，如何探究學習冪級數學生學習效果才更好方面等。