部分框支剪力墻結構轉換構件及上部剪力墻分析

朱德勝

（重慶建普城市建設發展集團有限公司，重慶400014）

0 引言

現代高層建筑中，由于底部要求設置大空間，上部框架柱或剪力墻不能直接連續貫通落地，需設置轉換層，在結構轉換層布置轉換結構構件。主要結構轉換方式有：梁式轉換、桁架轉換、厚板轉換等。梁式轉換具有傳力途徑明確直接、受力性能好、構造相對簡單、施工方便、結構設計相對容易等優點，被廣泛應用[1]。本文主要分析梁式轉換結構的轉換梁及上部剪力墻在豎向荷載作用下的內力、應力和變形，以及不同分析模型對分析結構的影響對比。

轉換構件由于承受上部多層柱或剪力墻傳遞的豎向、水平向荷載以及底部彎矩，轉換構件受力較大且較為復雜。水平轉換構件的豎向剛度（在豎向荷載作用下的變形）對上部被轉換的墻柱內力影響較大，過大的變形將導致上部豎向構件內力突變嚴重，使得上部被轉換豎向構件處于多向的復雜應力狀態，影響構件的抗震性能[2]。設置轉換層，結構沿豎向剛度發生突變，荷載傳遞途徑發生變化，荷載作用下轉換構件的內力集中，故轉換結構設計將重點關注轉換構件和其上部豎向構件的受力。

在做轉換層結構設計時，經常會遇到轉換層上一層的剪力墻墻肢軸力、水平“剪力”、彎矩很大甚至部分構件超限的問題，而轉換層以上二層墻肢內力又正常。本文采用midas Gen通用有限元軟件，以梁單元、板（殼）單元和實體單元模擬轉換梁，通過力學分析轉換梁及上部剪力墻的受力狀態，分析產生這種現象的原因。

1 分析模型

為探究轉換梁及上部剪力墻的力學現象及受力本質，采用一簡單規則的框架剪力墻結構，在一層通過轉換梁轉換上部剪力墻，采用不同的力學假定分析對比不同模型的內力情況。

采用12層框架剪力墻結構模型，平面尺寸采用對稱的2跨9m×9m，轉換梁尺寸400mm×1000mm，剪力墻厚度250mm，地震烈度7度（0.10g），場地II類，場地特征周期Tg=0.35s，阻尼比0.05，基本風壓0.4kN/m2，具體模型如圖1所示。

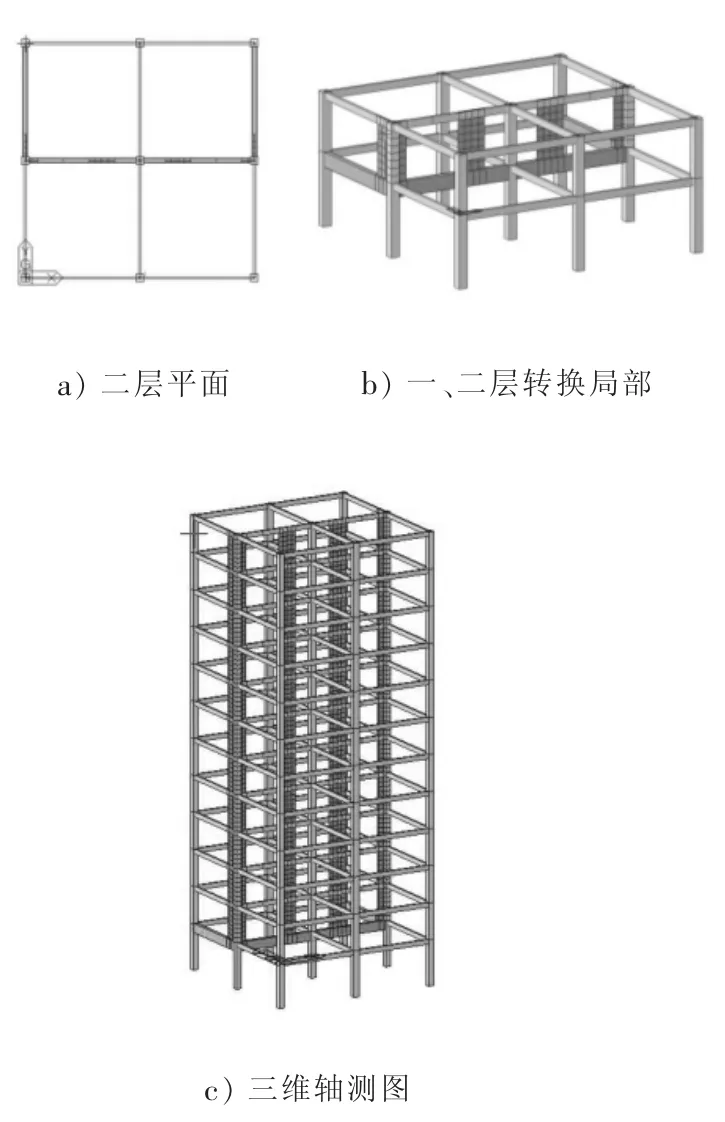
圖1 模型基本情況

轉換梁計算模型假定：模型一采用梁單元；模型二采用板單元；模型三采用實體單元。二層不考慮剛性樓板，為了更清晰了解轉換梁受力情況，也不考慮二層轉換層板厚，只考慮樓板導荷。轉換層上部剪力墻采用板單元模擬，midas Gen板單元能真實模擬墻面內、外剛度，可以進行水平和豎向有限元劃分，方便分析應力分布，真實反映墻體實際受力。

2 整體計算指標對比

2.1 周期對比

不同模型周期對比如表1所示。

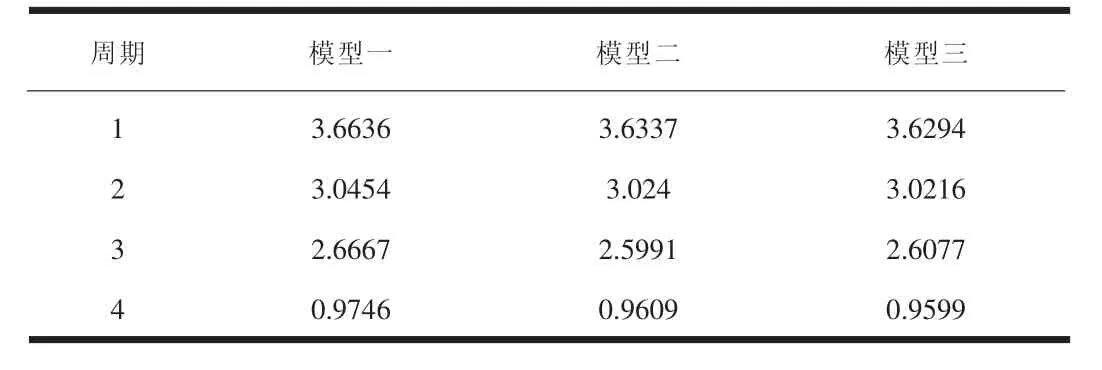
表1 不同模型周期對比

2.2 層間位移角對比

各模型層間位移角如表2、表3、表4所示（僅列出下部5層數據，經分析其余樓層規律基本相同）。

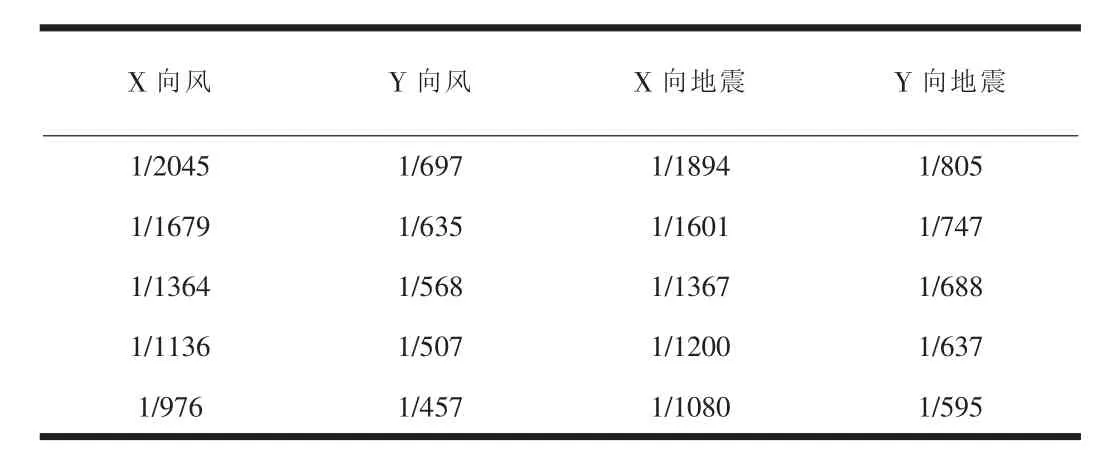
表2 模型一層間位移角

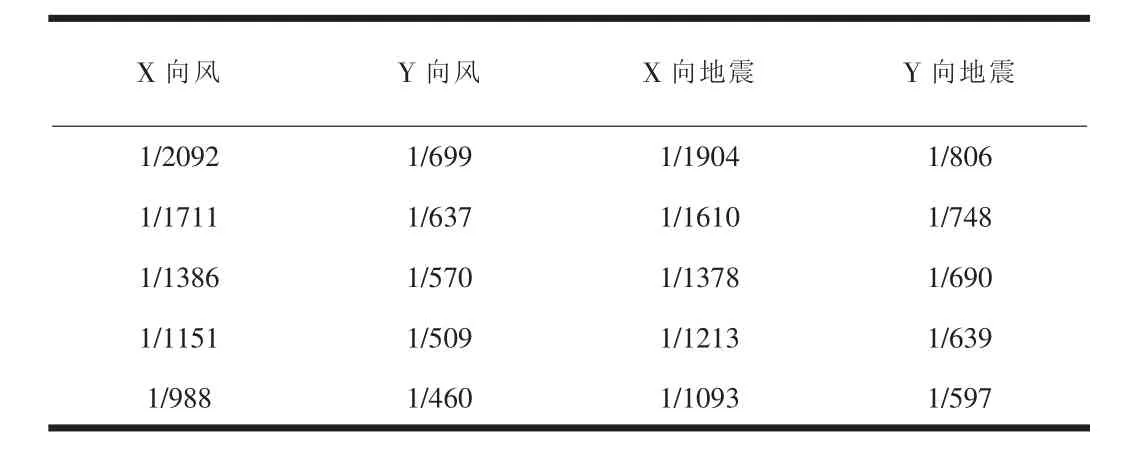
表3 模型二層間位移角

表4 模型三層間位移角

通過以上三個模型周期、層間位移角對比，不同的轉換梁模型假定計算的整體指標基本相同，誤差較小，故結構構件所分配的外力也基本相同，局部對比分析具有可行性。由于本次分析的重點是轉換梁及其上部剪力墻在豎向荷載作用下的力學現象和應力分布規律，采用模型較為簡單，實際工程中不同模型計算數據誤差可能會大于該模型。

3 轉換梁計算內力對比分析

選取中部轉換梁進行分析，由于此轉換梁分別在支座和跨中有承托的剪力墻，受力更具有典型性。具體轉換梁位置如圖2所示。

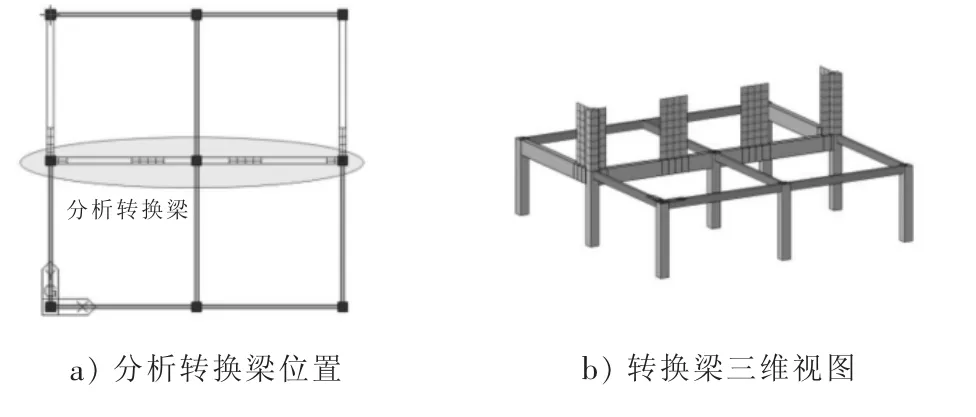
圖2 選取轉換梁位置

3.1 不同模型轉換梁內力對比分析

軟件只能顯示梁單元的內力計算結果，板單元和實體單元不能直接輸出內力結果，只能通過應力積分得到內力值[3]。板單元和實體單元模擬轉換梁在與上部剪力墻端交接處均出現局部應力集中，若以此處截面積分得到內力，會產生局部內力突變。為了能更真實反映不同模型真實受力情況，分別選取應力變化相對均勻的截面進行對比，如圖3截面1、截面2、截面3、截面4。對比結果如表5所示。

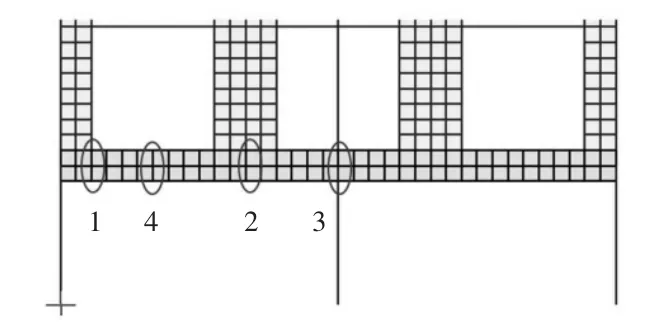
圖3 對比選取截面位置

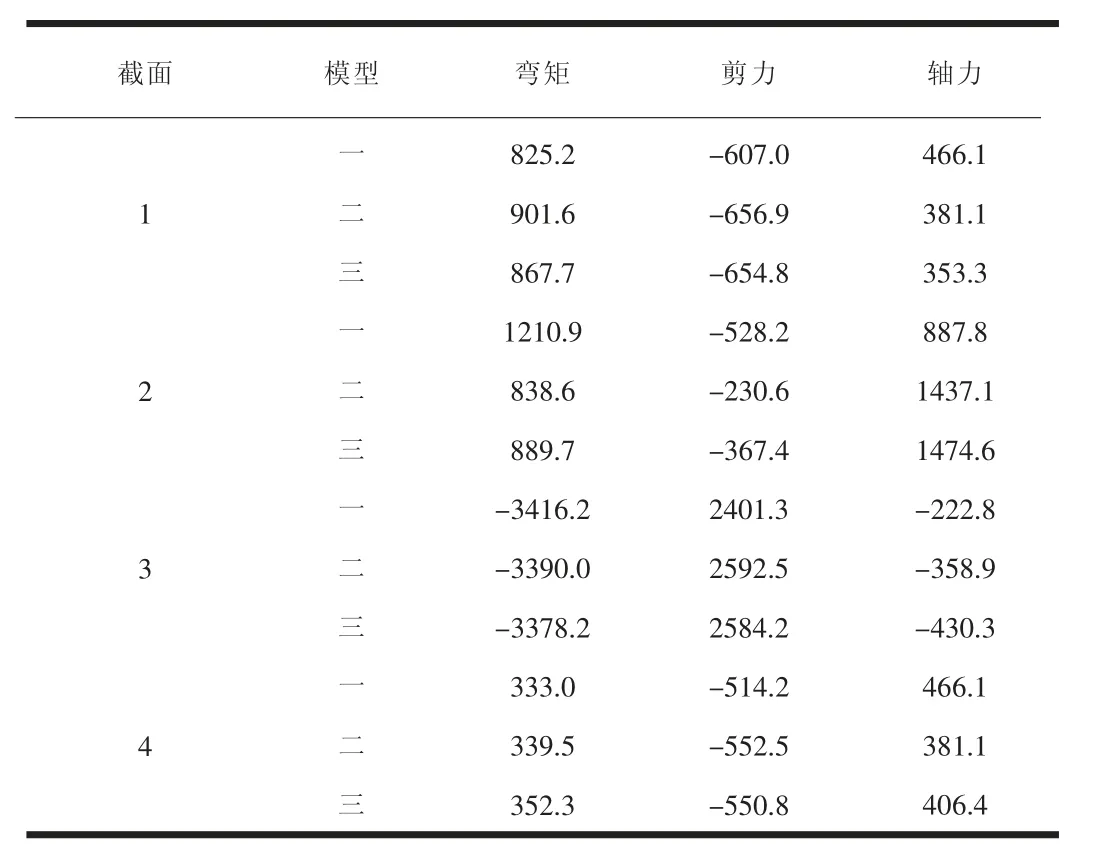
表5 工況（1.2恒+1.4活）單位（kN·m）

通過以上數據，發現板單元和實體單元模擬轉換梁計算結果較為接近，和梁單元計算結果相比，沒有特定規律，主要由被轉換剪力墻作用位置、轉換梁截面尺寸及抗彎剛度等因素決定，剪力墻作用范圍外轉換梁段及4截面計算結果比較接近。

3.2 不同單元模擬計算結果出現差異的原因

（1）單元自由度和邊界條件的差異。板單元每個節點具有x、y、z軸方向的移動的線性位移自由度和繞x、y軸旋轉的旋轉位移自由度，及板單元節點無平面內旋轉自由度[4]，故在板單元節點與兩端柱連接處只傳遞拉壓力，類似桁架單元連接，節點內力精度與有限元劃分數量及連接節點數量有關，連接節點越多精度越高。

（2）不同單元模擬轉換梁對截面尺寸的假定。有限元軟件梁單元截面尺寸僅提供軸向和抗彎剛度，及簡化為被賦予梁截面特性的位于中性軸的線單元，轉換梁上部的剪力墻實際與梁中性軸相連接，忽略了梁的尺寸效應，在支座節點僅能保證與梁柱的中性軸轉角位移相協調，梁頂和梁底節點與之相鄰的柱實際轉角位移是不協調的。轉換梁頂面與剪力墻底端節點實際位移也是不協調的，故梁單元模擬轉換梁計算結果有一定近似性。板單元和實體單元模擬的轉換梁頂與上部剪力墻按實際連接，可以做到接觸面的變形協調，計算結果更合理。

以上三種模型計算結果轉換梁均出現較大軸力，且同一跨梁被上部剪力墻節點分割后出現拉力和壓力，受力類似于桁架下弦桿，剪力墻類似于腹桿。在框支剪力墻結構設計分析計算時，轉換層樓板應按彈性板考慮，這樣才能真實計算出轉換梁軸力，轉換梁按拉彎或壓彎構件考慮，若按剛性樓板考慮，樓板平面內節點剛性約束于樓板形心處，面內無變形，不能真實反映轉換梁及其上部剪力墻的受力情況。由于轉換梁受力復雜且重要，轉換層樓板構造厚度較大，在實際設計時為提高轉換梁安全儲備，軟件在模型假定時可能導致計算結果不確定，可以偏安全地不考慮樓板的影響，所有軸向力由轉換梁承擔。《高規》10.2.7也規定轉換梁應加強梁上部通長筋和兩側腰筋[5]。

由于不同單元假定計算結果有一定差異，在剪力墻與下部轉換梁連接處內力突變嚴重，《高規》5.1.15條文中明確說明，對轉換構件等受力復雜部位應按應力分析結果進行截面配筋設計校核。

4 轉換梁上部剪力墻變形、應力分析

在轉換層結構分析時，經常遇到轉換梁上一層墻體內力突變（軸力、“剪力”、彎矩），配筋異常大甚至截面超限，上部樓層卻受力合理的現象。可從轉換梁及其上部墻體的應力分布和變形分析其原因。

由于梁單元不能進行有限元剖分，不能得出應力分布情況。板單元能真實模擬面內面外剛度，剖分后可以得出應力分布規律。轉換梁和上部剪力墻均采用板單元[6]，能夠真正做到節點變形協調、分析結構可靠。

4.1 豎向荷載作用轉換梁和上部剪力墻豎向變形

豎向荷載作用下，轉換梁產生豎向變形，由于梁上各點變形差異導致上部剪力墻發生彎曲變形（圖4）。

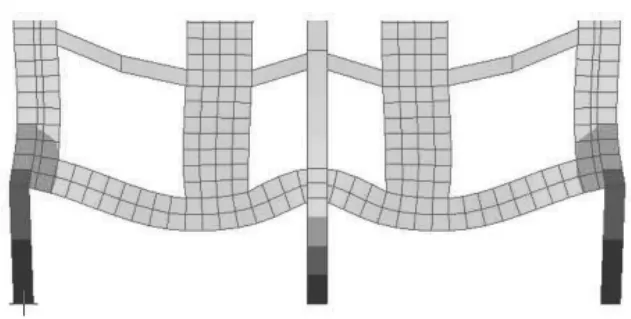
圖4 1.0恒+1.0活作用下豎向變形

4.2 豎向荷載作用下剪力墻應力分布

截取轉換梁及上部剪力墻在豎向荷載作用下的應力分布，如圖5所示。

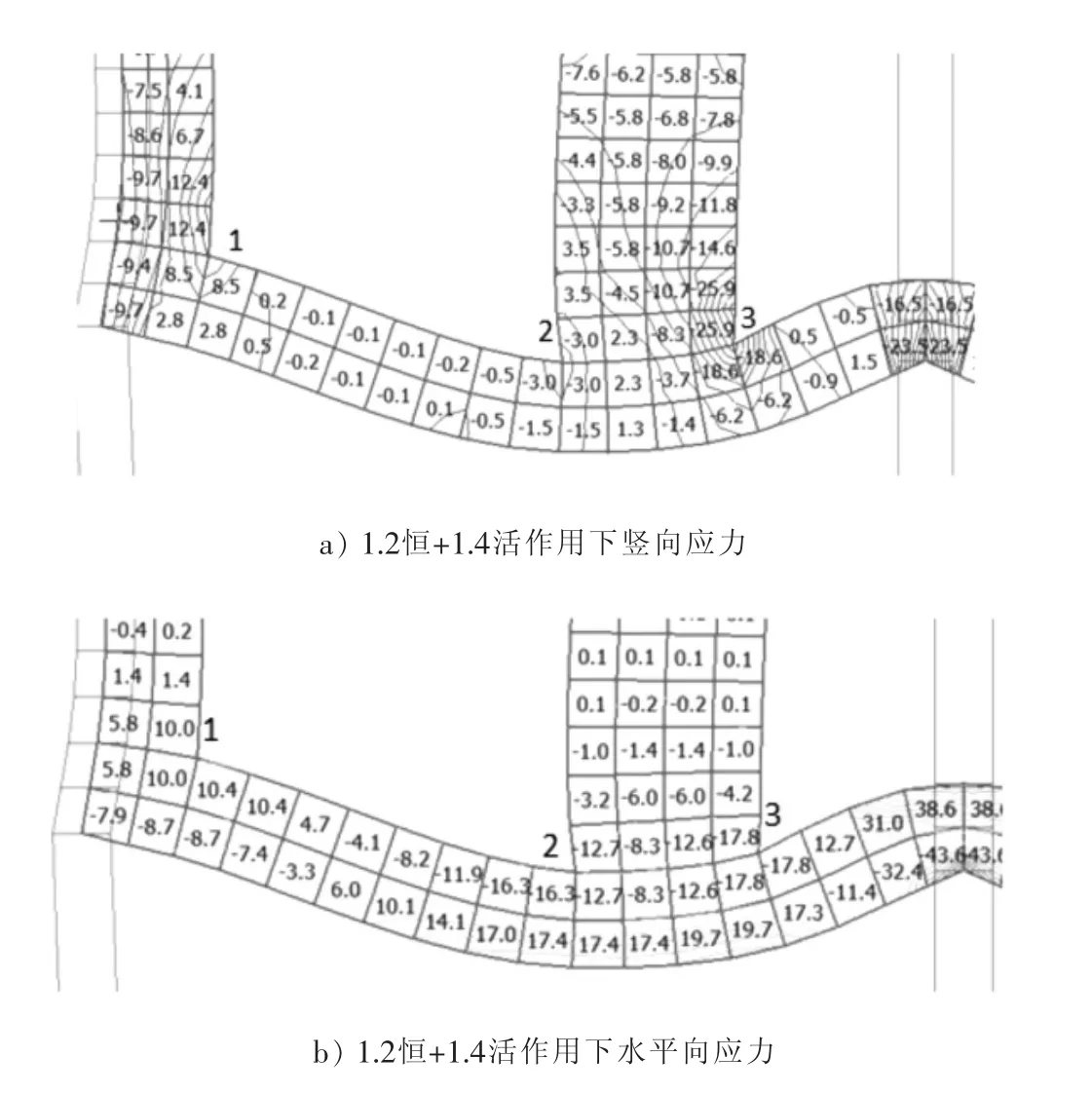
圖5 1.2恒+1.4活荷載作用下應力分布

剪力墻端部與轉換梁連接處均出現較大應力突變，其中1位置處剪力墻在豎向荷載下出現較大拉壓力，主要由于轉換梁向下變形導致局部剪力墻受拉，3位置轉換梁轉角位移較大，導致上部剪力墻單元發生較大變形，應力突變明顯，相應轉換梁單元也發生較大局部壓應力。這就能很好解釋轉換層上部剪力墻軸力突變軸壓比超限現象。

在豎向荷載作用下，轉換層上部剪力墻由于水平向受到轉換梁約束，最左側墻肢的左端節點位于柱截面范圍內，豎向變形較小，在1位置處右端節點位于跨中產生豎向變形，從而導致水平向出現較大拉壓力[6]，這就解釋了支座處轉換的剪力墻為何有時會出現“剪力”超限問題，墻肢越長越明顯，此“剪力”并非由水平向荷載作用產生，而是由豎向荷載作用下兩端產生變形差導致墻體受拉。2、3位置位于轉換梁跨中，豎向荷載作用下產生明顯的擠壓變形，水平向出現較大壓應力，特別在3位置處，單元受到較大豎向壓應力和水平向壓應力，最大主應力將發生在斜截面上，σ1∶最大的主應力=，若此時剪力墻軸壓比僅按豎向荷載作用計算，斜截面實際主壓應力大于豎向壓應力值，從而導致斜面上的軸壓比超過規范值[7]，剪力墻在地震作用下延性降低，存在一定安全隱患。一般規律是轉換梁負彎矩區梁頂面受拉，相應剪力墻受到水平拉力，正彎矩區梁面受壓，上部剪力墻水平受壓，也可理解為轉換梁應力擴散至上抬剪力墻。

對于轉換梁上部剪力墻應力突變，可以通過轉換和不轉換兩種方式進行對比。在豎向荷載作用下（1.2恒+1.4活）墻體應力、內力如圖6所示。

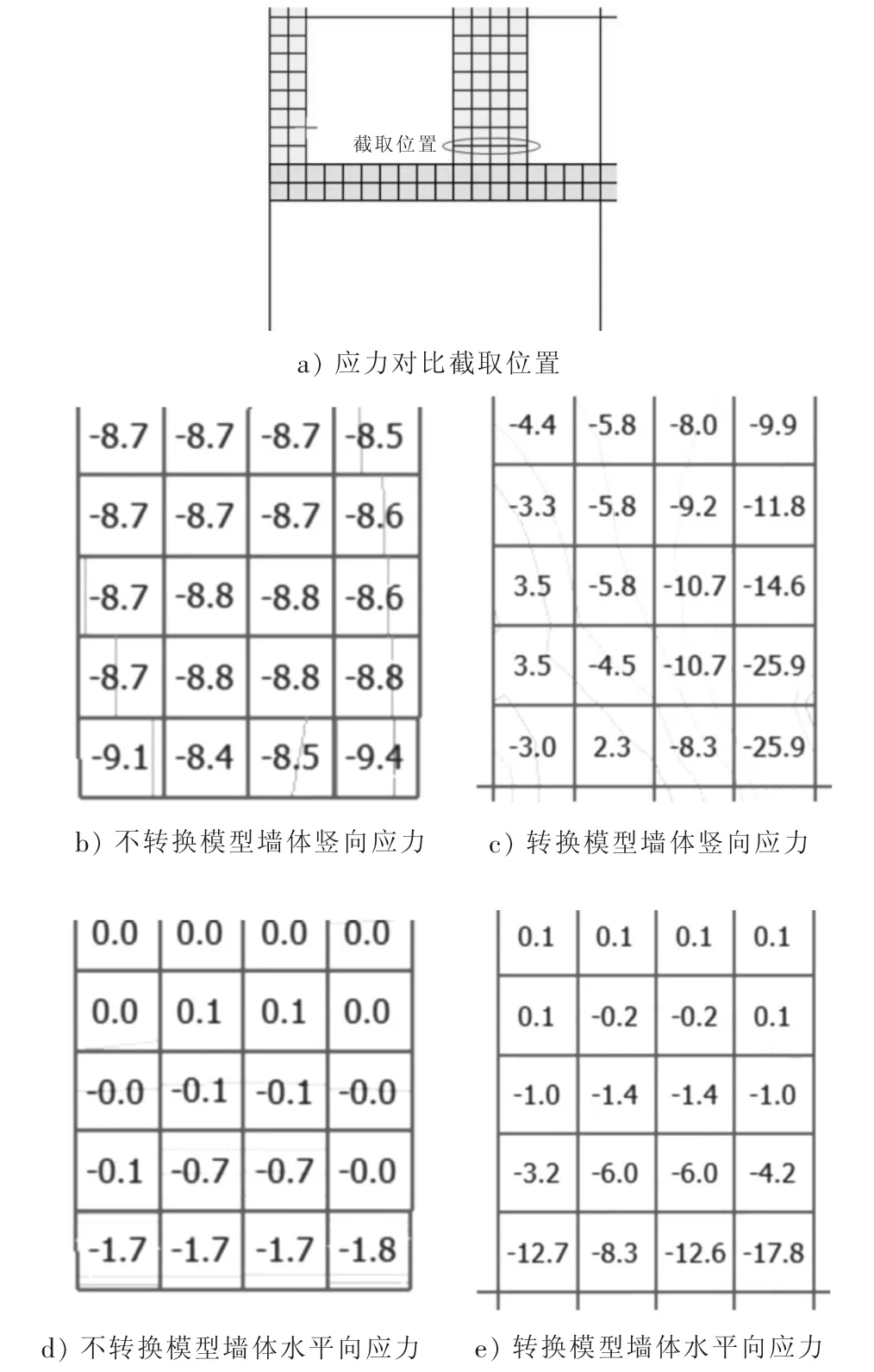
圖6 轉換和不轉換墻體應力對比

轉換與非轉換剪力墻底端截面內力對比如表6所示。

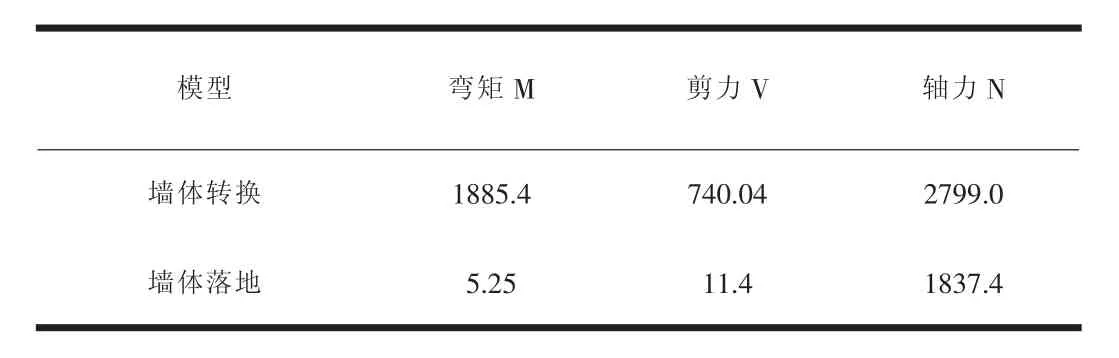
表6 墻體落地與墻體轉換內力對比

通過對以上兩種模型剪力墻體應力分布和內力提取可知，轉換層上部剪力墻局部應力集中，從而導致內力突變。根據前文所述，應力突變的原因是，轉換梁的豎向變形使上部剪力墻兩端變形不一致，導致平面內整體彎曲。提高轉換梁抗彎剛度可緩解應力突變，但不能根本消除。

因為轉換梁上部墻體的內力突變是由豎向荷載引起的，故在設計時不能忽視此影響，應通過有限元計算，按應力配筋，對于出現水平拉應力較大的墻體，應配置水平鋼筋承擔此拉應力。對于出現水平壓應力較大的墻體，由于墻體處于豎向和水平向雙向應力狀態，最大主應力出現在斜截面上，故應按斜截面上正應力驗算剪力墻軸壓比。建議不要在轉換層上部的墻體內開洞，若不能避免，應按剪力墻開洞的模型驗算剪力墻以及下部的轉換梁應力，轉換梁上部墻體除計算要求外構造加厚。

5 結論

（1）用梁單元、板單元和實體單元計算框支剪力墻結構整體指標時，結果基本一致。

（2）轉換梁用梁單元、板單元和實體單元模擬計算時，結果有一定差異，特別在上部剪力墻與轉換梁接觸處差異更大，這主要由于不同計算單元模型假定以及邊界條件不同，故轉換梁配筋采用多模型對比驗算并加強構造配筋很有必要性。

（3）豎向荷載作用下，由于上部剪力墻體與下部轉換梁豎向變形相協調，產生整體彎曲變形，導致轉換梁上一層剪力墻應力突變，墻體水平向產生較大拉（壓）力，平面內產生較大彎矩和附加軸力，墻體配筋建議根據應力計算結果驗算復核，軸壓比建議按照斜截面組合壓力驗算。

（4）由于轉換梁上一層剪力墻受力復雜，設計上建議墻體加厚，盡量避免墻體開洞，避免采用一字形墻肢。