基于大數據方法的持液率預測模型

鄭 琳 劉 云

長江大學石油工程學院, 湖北 武漢 430100

0 前言

管道中氣體和液體的兩相流在石油工業中經常發生,多相管流一直是石油工業中的一個重要問題[1]。持液率是指管道內實際的液體體積分數,是計算壓力損失時最重要的參數,同時也對預測水合物的形成和蠟的沉積十分重要[2]。對于持液率的預測,國內外學者提出了大量的機理模型和經驗模型,部分使用較普遍,而另一部分的應用范圍則較窄。大部分的方法都始于流態的預測,每種流態都有相關的預測持液率方法,但這種方法取決于流型預測的準確性,且在跨流型過渡邊界,會出現預測模型不連續問題,模型隨著流動條件的變化會出現差異,使得選擇最合適的流動相關性模型具有挑戰性。

持液率與其影響參數之間是一種非線性關系,與神經網絡模型所表達的解決非線性映射問題的思想相吻合[3]。Osman E A[4]開發的神經網絡模型使用4個輸入參數，即氣體表觀速度、液體表觀速度、壓力和溫度,包含12個隱含層節點。Shippen M E等人[5]排除氣體密度、氣體黏度、管壁粗糙度等幾個對持液率影響可忽略的變量,并加入無滑移持液率共7個輸入層變量,包含8個隱含層節點，都與現有的經驗模型和機理模型預測的持液率結果進行了比較,證實神經網絡模型在預測持液率方面是最準確的。但是Osman E A使用的輸入參數中沒有包括流體特性,這就代表只能應用于具有類似實驗特性的流體中。Shippen M E在此基礎上進行了改進,加入流體特性,使模型的使用范圍不再局限于特定流體特性,但還是受到了訓練數據范圍的影響。在這些情況下,我們采用大數據統計的方法并使用Eaton B A提出的流體特性相關無因次數作為輸入參數,擴大模型的使用范圍。建立好的GA-GRE-BP神經網絡模型經過大數據集訓練后得到持液率預測公式,最后利用隨機得到的70組實驗數據驗證了新模型的準確性。

1 GA-GRE-BP神經網絡模型

1.1 BP神經網絡的構建

Ros N C J[6]在大量實驗和理論工作的基礎上,排除了持液率可以忽視的,氣體密度,氣體黏度和壁面粗糙度等幾個變量。Shippen M E等人[5]也在神經網絡模型的研究過程中證實這些變量的影響較弱,可忽視。其余不可忽視變量包括液體表面張力、管徑、液體黏度、氣體表觀速度、液體表觀速度和液體密度。考慮到數據的局限性,為了擴大BP神經網絡模型的使用范圍,決定利用Eaton B A等人[7]提出的無因次參數量作為BP神經網絡的輸入變量,對數據有較好的適應性。

Eaton B A等人提出的持液率相關公式為:

(1)

式中:Ψ為任意函數；HL為持液率;Nlv為液體速度影響數;Ngv為氣體速度影響數;Nd為管徑影響數;p為絕對壓力,MPa;pb為測量氣體的基準壓力,MPa;Nl為液體黏度影響數;Nlb為基礎黏度影響數,取0.002 26。

除了選取氣體速度影響數、液體速度影響數、管徑影響數和液體黏度影響數以外,還加入了壓力影響因素,共5個因素作為輸入層變量。

BP神經網絡模型建立的關鍵環節是隱含層的個數,為了避免過多或過少的隱含層神經元個數對神經網絡模型的建立帶來的不利影響,隱含層神經元的個數通過以下的經驗公式確定[8]:

(2)

式中:m為隱含層神經元的個數;n1為輸入層神經元的個數;n2為輸出層神經元的個數;a為0～10之間的常數。

經過反復測試對比,確定隱含層神經元的個數為7,當隱含層激活函數為S型且輸出范圍在-1～1的‘tansig’函數,輸出層激活函數為線性輸出的‘purelin’函數,選擇訓練函數來導出動量并自動調整學習率旋轉梯度遞減函數為‘trainlm’的時候準確度最高,最終確定神經網絡模型為5×7×1的三層感知器的結構形式,圖1為持液率的神經網絡示意圖。

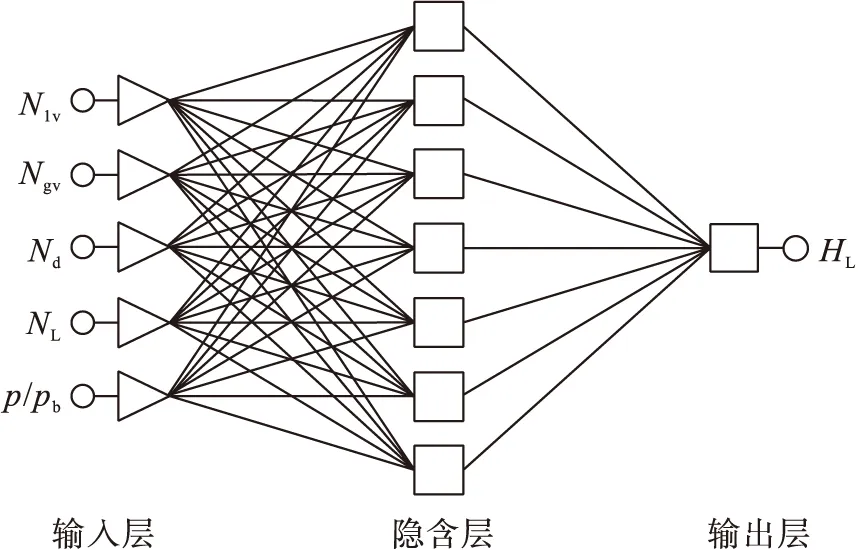
圖1 持液率的神經網絡示意圖Fig.1 Neural network diagram of liquid holdup

1.2 GRE-BP神經網絡的構建

灰色關聯熵分析是熵權法與灰色關聯度相結合的一種模型。熵權法的引入不僅降低了灰色關聯度系數的波動性影響,也提高了灰色關聯分析法的計算精度[9]。經過灰色關聯熵處理過的參數用于BP神經網絡模型的訓練降低模型預測誤差,從而彌補基本的BP神經網絡存在的缺點。

1.2.1 熵權法

熵權法是一種利用信息熵來度量影響持液率各個因素的客觀賦權法,一個因素的信息熵越小,其無序化程度就越大,表明它所提供的有用信息越多,對持液率的影響力越大,權重也就越高。熵權是由各影響因素信息效用值確定的[9]。熵權的運算步驟如下:

1.2.1.1 標準化處理

(3)

式中:yij為經過標準化處理的第i個單位第j個因素值;xij為第i個單位第j個因素數據原始值;xjmin為第j個因素的最小值;xjmax為第j個因素的最大值。

1.2.1.2 定義標準化

(4)

式中：Yij為經過定義標準化處理的第i個單位的第j個因素的值。

1.2.1.3 因素的信息熵值計算

(5)

式中:ej為第j個因素的信息熵值。

1.2.1.4 影響因素的信息效用值計算

dj=1-ej

(6)

式中:dj為第j個因素的信息效用值。

1.2.1.5 評價影響持液率因素的權重

(7)

式中:wj為第j個因素的權重。

1.2.2 灰色關聯度分析

灰色關聯度能反映兩種指標之間的相關程度。簡單來講,把持液率作為參考序列,而影響持液率的5項指標就是比較序列,最后通過灰色關聯度分析可以得到這5項指標分別與持液率的相關程度,灰色關聯度越大,說明它對持液率結果的影響力越大。灰色關聯度的運算步驟如下:

設Xi={xi(k)|k=1,2,…,n}為比較序列,X0={x0(k)|k=1,2,…,n}為參考序列。

1.2.2.1 數據無量綱化處理

消除不同因素序列可能存在量綱不同而產生的差異，需要對原始數據進行無量綱化處理。

1.2.2.2 求差序列

Δ=|x0(k)-xi(k)|,k=1,2,…n

(8)

式中:Δ為各時刻xi與x0的絕對差值。

1.2.2.3 計算灰色關聯系數

(9)

式中:ξi(k)為第i個比較序列第k個指標與參考序列第k個最優指標值的關聯系數;ρ∈(0,1)為分辨系數,一般取0.5;Δmin為兩級最小差,且Δmin=miniminkΔ;Δmax為兩級最大差,且Δmax=maximaxkΔ。

1.2.2.4 計算灰色關聯度

(10)

式中：γi為第i個比較序列的灰色關聯度。

通過熵權法與灰色關聯度的結合,求得灰色關聯熵公式如下:

hi=wj×γi

(11)

式中：hi為第i個指標的灰色關聯熵。

1.3 GA-GRE-BP神經網絡的構建

由于學習效率低和容易陷入局部最小值等問題仍然存在于GRE-BP神經網絡中,為了避免這些情況的發生,利用遺傳算法可以全局尋優的特點對神經網絡的權值和閾值進行優化,同時也能加快算法收斂的速度,縮短網絡訓練的時間[10]。

遺傳算法是借鑒生物界進化規律設計的算法,它通過數學方式,利用計算機編碼完成染色體的選擇、交叉和變異,從而求取最優個體。遺傳算法個體的編碼長度取決于優化的權值和閾值的個數,并最終由最佳GRE-BP神經網絡中輸入和輸出的參數個數決定[3]。最后被遺傳算法優化后的權值和閾值用于GRE-BP神經網絡訓練。

GA-GRE-BP神經網絡模型流程見圖2。

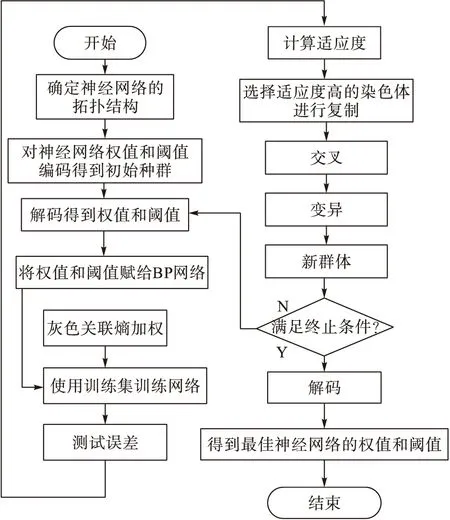
圖2 GA-GRE-BP神經網絡模型流程圖Fig.2 Flowchart of GA-GRE-BP neural network model process

2 模型驗證

完成GA-GRE-BP神經網絡模型的建立后,將眾人研究的4 010組數據用于開發氣液兩相流動中持液率的神經網絡預測模型,隨機選出70組數據作為測試集,用于測試該神經網絡模型的準確性,剩余3 940組數據作為訓練集,用于訓練該神經網絡模型。表1為實驗數據的來源以及一些流動參數的有效范圍。

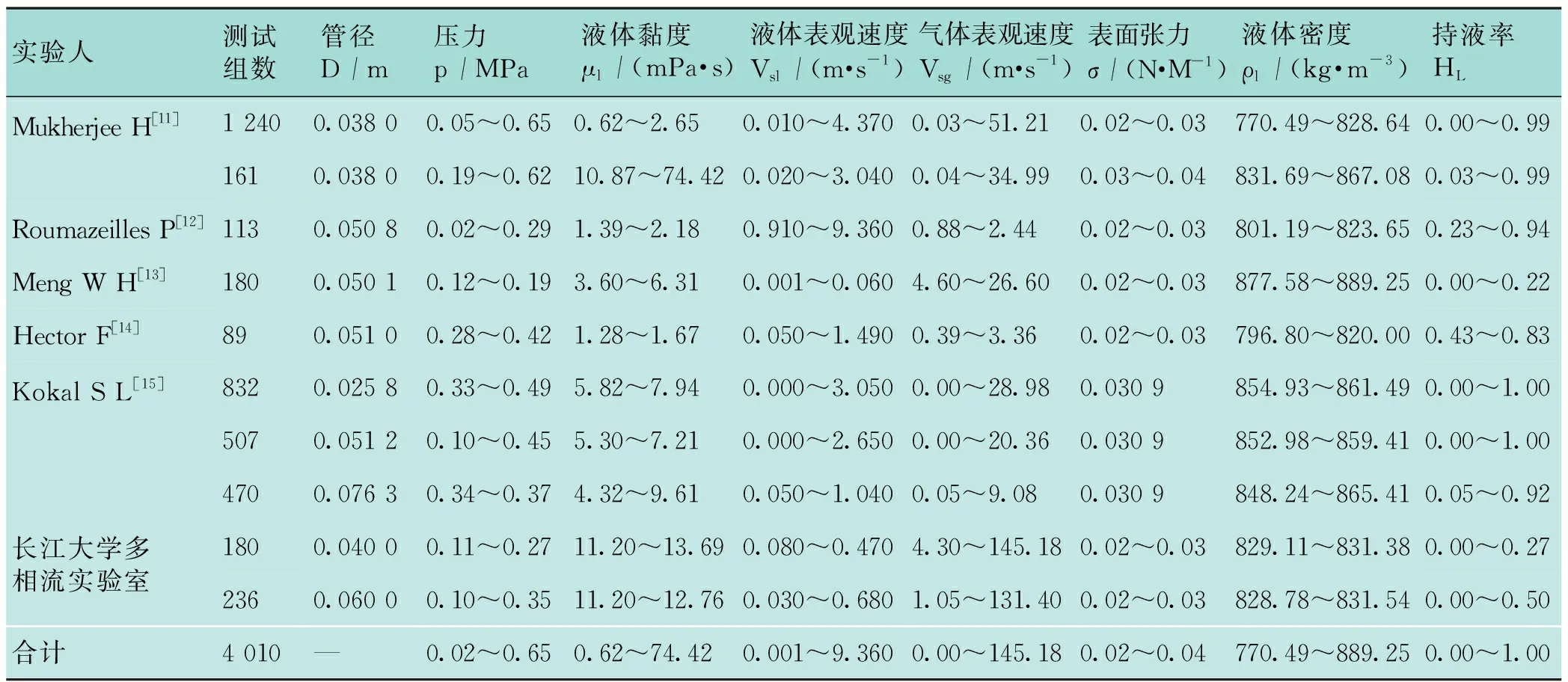
表1 實驗數據匯總表

以上實驗室數據通過長江大學多相流實驗平臺得到,此平臺可開展在不同傾角、不同溫度和壓力等多個條件下，對油、氣和水三相混合介質多相管流動態研究,實驗流體為白油和空氣,通過實驗系統的動力系統、管路系統、控制系統、儲存系統和數據采集系統等共同完成[16]。

2.1 交叉驗證

神經網絡幾乎依靠數據單純的訓練并記憶,不能夠對數字本質進行理解并泛化到測試集上,本質只是一個經驗性的模型。因此選取交叉驗證的方式來評估優化后的模型。K折交叉驗證誤差取決于K值的大小,K值較小時,誤差較大,當K值較大時,與留一法交叉驗證相當,鑒于留一法交叉驗證的過程較長,采用與留一法交叉驗證更接近的10折交叉驗證[17]。

10折交叉驗證是把訓練集里的3 940組數據均分成10個不相交的子集,每一個子集里有394組訓練數據,依次從分好的子集里面,拿出1個作為驗證集,其他9個作為訓練集訓練神經網絡模型,并使用此驗證集對訓練算法的行為進行獨立檢查,最后平均10次的結果作為誤差的估計,來判斷模型的準確度。

2.2 驗證結果

通過對GA-GRE-BP神經網絡模型進行訓練、驗證,得到與模型相關聯的權值和閾值，見表2～3。

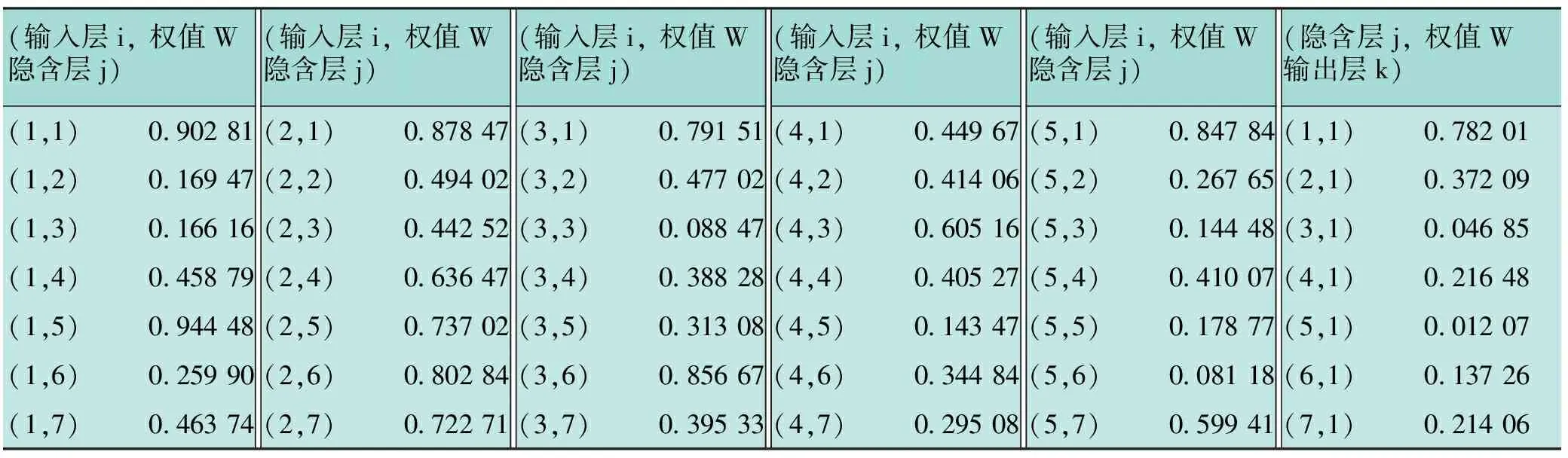
表2 輸入層、隱含層和輸出層之間的權值表

表3 隱含層和輸出層的閾值表

將得出的權值和閾值與持液率預測模型的嵌套數學公式結合,得到持液率的預測公式如下:

(12)

式中:HL為持液率；Wij為第i個輸入層元素到第j個隱含層元素之間的權值；Bj為第j個隱含層元素的閾值；xi為輸入層的第i個元素；Wjk為第j個隱含層元素到第k個輸出層元素之間的權值；Bk為第k個輸出層元素的閾值。

(13)

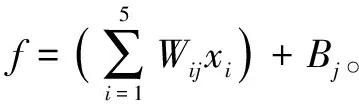
3 模型預測

為了對GA-GRE-BP神經網絡模型的準確性以及可行性進行評估,將其與基本的BP神經網絡模型，以及Beggs-Brill[18]和Minami-Brill[19]提出的傳統模型進行對比。表4是各指標的灰色關聯熵,用于GA-GRE-BP神經網絡模型的預測。

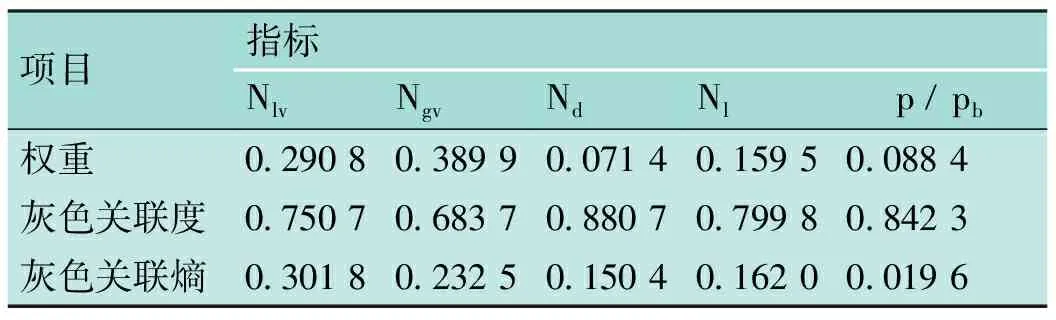
表4 各指標的灰色關聯熵表

圖3為持液率的實際值與各模型預測值對比結果。從圖3可以看出,Minami-Brill的模型在持液率較低和較高的范圍內預測結果較好;Beggs-Brill的模型雖然在整個持液率的范圍內預測結果較好,但仍然存在許多誤差較大的預測點;BP神經網絡模型和GA-GRE-BP神經網絡模型的預測值均在實際值曲線附近,整體來看,GA-GRE-BP神經網絡模型預測結果更好。

圖3 四種模型預測對比結果圖Fig.3 Four models predictions and comparison results

為了更好地進行模型對比,同時采用Mandhane J M[20]等人提出的五種不同誤差測量方法來評估預測的準確性。

1)均方根誤差：

(14)

2)平均百分比誤差：

(15)

3)平均絕對百分比誤差：

(16)

4)絕對值平均絕對誤差：

(17)

5)平均絕對誤差：

(18)

式中:ei為持液率預測值與實際值的差值,即ei=(HLpred-HLmeas)i,i=1,2,…,n；HLpred為持液率預測值;HLmeas為持液率實際值。

四種持液率預測模型的誤差對比見表5，由表5可看出,BP神經網絡模型比傳統模型的預測更精確,而GA-GRE-BP神經網絡模型相較于BP神經網絡模型,誤差均降低了40%以上,提高了模型的精確度。

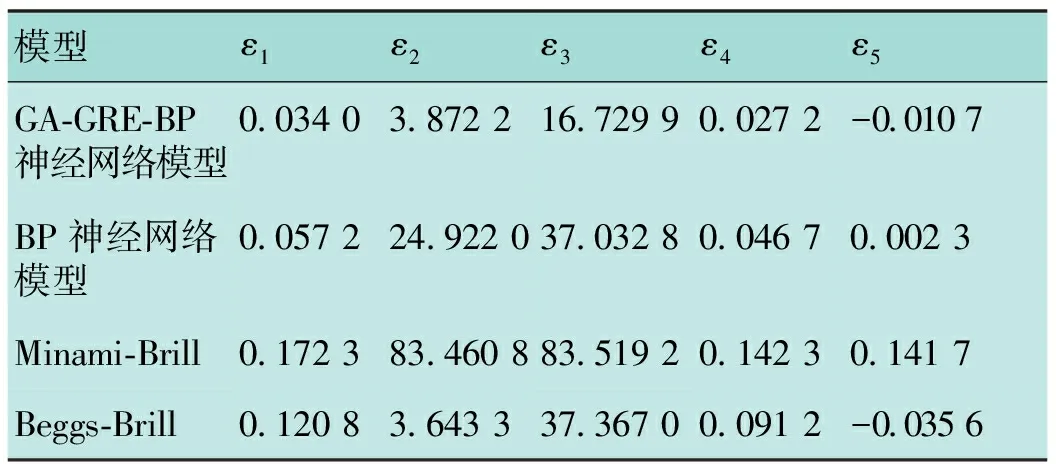
表5 四種持液率預測模型的誤差對比表

綜上所述,GA-GRE-BP神經網絡模型不僅精確度高,而且應用范圍廣,可以用來預測持液率。

4 結論

1)GA-GRE-BP神經網絡模型預測氣液兩相流持液率,利用龐大的數據體系,數據來源多樣化,更有效地預測處于各種流體特性下氣液兩相流的持液率。將Eaton B A等人提出的無因次參數作為輸入層變量,不僅解決了數據局限性問題,也使得模型的適應性更好。

2)經過大數據集訓練的GA-GRE-BP神經網絡模型,最終得到了一個嵌套型數學公式,可以直接用于氣液兩相流持液率的預測。

3)基于大數據方法的GA-GRE-BP神經網絡模型彌補了基本BP神經網絡模型預測誤差大,容易陷入局部極值的缺點,它的精確度更高,收斂速度更快;彌補了傳統模型應用范圍的狹窄,迭代計算復雜的缺點,它的應用范圍更廣泛,使用更簡便。

4)基于大數據方法的GA-GRE-BP神經網絡模型是依靠大量數據,單純訓練學習的一個過程,如何對已有數據進行處理并加以充分利用,提高精確度,是后續要完善的一項任務。