應力路徑對飽和砂土動力特性影響的試驗研究*

陳曉飛，吳建翔，李 園

揚州市市政建設處，江蘇 揚州 225000

在地震或者車輛荷載作用下，若孔隙水壓力來不及消散，砂土可能出現液化現象，導致地基失穩，因此砂土的抗液化特性得到了學者的廣泛關注。董正方等[1]分析了不同圍壓、干密度和細粒含量下粉砂土的動強度和抗液化強度曲線。李濤等[2]基于動三軸的液化試驗研究了黏粒和粉粒對砂土液化特性的影響。目前，相關認識主要是根據循環三軸或循環扭剪[3-4]試驗結果得到的，但這些試驗只考慮單個方向上出現循環受載的情況，對于復雜應力路徑下砂土動力特性的研究尚顯不足。例如海洋工程中，波浪荷載在地基中產生的加載路徑與在循環三軸和循環扭剪中的有明顯區別，其抗液化特性與現有認識有何不同尚不清楚。因此，研究不同加載路徑對飽和砂土動力特性的影響是有必要的。

1 試驗概況

1.1 試驗儀器

文章研究的試驗儀器為英國GDS公司生產的空心圓柱扭剪儀（Hollow Cylinder Apparatus），該儀器可以分別控制作用在試樣上的靜、動豎向荷載和扭轉彎矩，作用在圓柱試樣的內、外壓力可以獨立控制。動力加載的強度一般通過循環應力比CSR表示，其表達式如下：

考慮到模擬波浪荷載的要求，需要同時施加豎直的豎向荷載以及試樣橫斷面上的扭轉荷載，為了更好地描述三維循環受剪狀態，采用張建民[5]的建議，同時體現豎向應力和環向應力的偏差，以及扭轉剪應力，動剪應力確定為

1.2 應力路徑的實現方法

試驗中共考慮循環三軸、循環扭剪和波浪荷載（圓耦合）3種應力加載路徑。循環三軸和循環扭剪可分別通過控制軸向力和扭矩實現，模擬波浪荷載的圓耦合路徑是指平均應力-偏應力坐標系中應力路徑為圓形，也即軸向動應力和扭轉剪應力幅值相當，相位差維持在90°[6]。

1.3 試驗土樣及方案

試驗所用砂為福建標準砂，物理參數如表1所示。

表1 土樣性質

土樣為內徑60mm、外徑100mm、高度100mm的空心圓柱試樣，采用落砂法制作。為分析相關因素的影響，試驗中考慮了松砂和緊砂2種密實程度的試樣，研究了3種動應力水平，以及3種加載路徑下土體抗液化能力，試驗方案及編號如表2所示。

表2 試驗方案

1.4 試驗過程

試驗中首先將試樣在0.5MPa的反壓下飽和，空心圓柱的內、外壓力同步設置為0.6MPa，待試樣在0.1MPa的有效平均壓力下固結穩定后，關閉排水閥，讓試樣在不排水條件下承受動剪應力作用，當孔壓達到有效平均應力的0.95時[7]，即認為土樣破壞。為保證試驗中孔隙水壓力在試樣中盡可能平衡，加載頻率取較低的數值，為0.1Hz，也即10s中加載1周。

2 試驗結果及分析

2.1 圓耦合試驗結果

（1）超靜孔隙水壓力。試驗7（相對密實度Dr=0.6，CSR=0.1）的超靜孔隙水壓力的發展曲線如圖1所示。由圖1可知，當振動周次小于21周時孔壓隨著振動周次的增加而穩定增加；當振動周次達到21周時，孔壓的增長隨著振動周次的增加明顯變快；當振動周次達到25周時，循環孔壓達到了30.49kPa，峰值孔壓達到了94.79kPa，此時試樣已經液化。

圖1 試驗7的超靜孔隙水壓力曲線

（2）動強度。砂土的動強度有多種定義方式，文章采用常用的方法，即某一加載周數下砂土不出現液化現象所能承擔的極限動應力比CSR。圓耦合的試驗結果如圖2所示。為便于后續分析，其他加載方式下的數據一并在圖2中給出。為了清楚表達，橫坐標加載周數用對數坐標表達。

圖2 動強度曲線

結果表明，加載路徑對砂土抗液化能力有比較明顯的影響。若循環應力比相同，波浪荷載（圓耦合）加載方式下，砂土最容易液化；循環三軸荷載條件下的砂土最難液化，循環扭剪下砂土的抗液化能力居中。從數值上來看，圓耦合的液化周次遠小于其他2種加載試驗，如當CSR為0.05時，圓耦合、循環扭剪和循環三軸下的結果分別為800、5450和20156周。

圖2還表明，在某一特定的加載方式下，達到液化所需要的加載周數隨著動應力水平的減小而顯著增加，在半對數坐標下都近似為線性關系。為便于工程應用，將試驗結果用下式進行擬合：

式中：c、d為試驗參數，不同的加載方式對應的試樣參數有所區別。循環三軸、循環扭剪、波浪荷載下的c分別為0.1796、0.1935、0.1442；d分別為 -0.013、-0.017、-0.013。

實驗結果表明，在不同的加載方式中，波浪荷載所對應的應力旋轉圓耦合加載路徑最容易使砂土液化，超靜孔隙水壓力發展得最迅速。一般認為，不排水條件下的孔隙水壓力大小和發展規律與塑性體積應變有密切的聯系。這意味著即使偏應力大小保持不變，但應力主軸的方向發生了明顯偏轉也會引起土樣的體積顯著減小，使相應試驗土樣發展出的塑性體積應變最大，這一影響在工程設計分析中需要被深入考慮。

2.2 應力路徑對液化周次的影響

不同砂土密實度下，3種應力路徑的孔壓發展曲線如圖3、圖4所示。結果表明，在同一CSR下，圓耦合應力路徑作用的孔壓發展更快。在CSR=0.1時，圓耦合路徑下的液化周次達到25周后試樣就已破壞，而動三軸和動扭剪對應的液化周次分別為510和275。不同的應力路徑下的孔壓總是隨著加載次數的增加而增加，但圓耦合增加得更快，可能是圓耦合應力路徑旋轉的同時發展了軸向應變和剪切應變。其他CSR作用下也呈現出相似的現象。為便于分析，匯總了不同加載方式下的破壞周次，如表3～表5所示。

表3 循環三軸試驗的液化破壞周次

表4 循環扭剪試驗的液化破壞周次

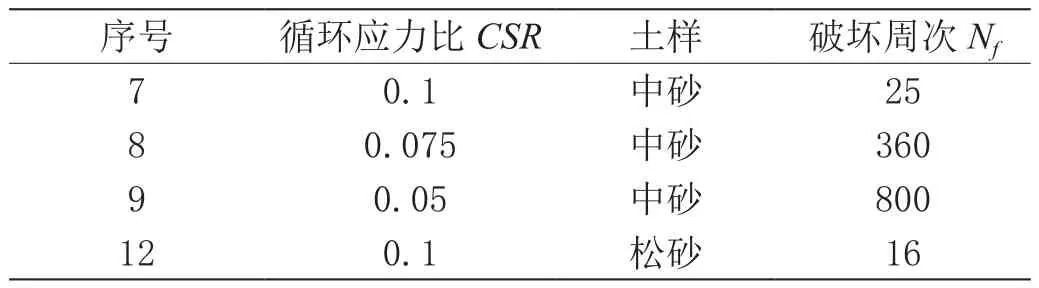
表5 圓耦合試驗的液化破壞周次

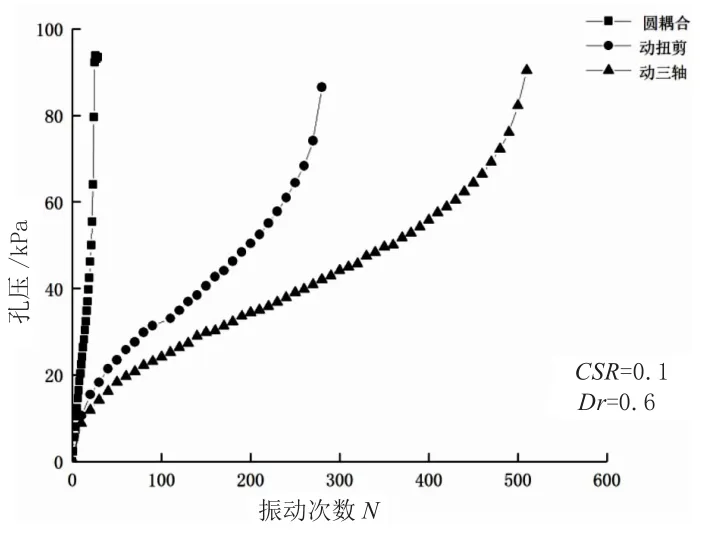
圖3 CSR=0.1的中砂孔壓發展規律

圖4 CSR=0.1的松砂孔壓發展規律

2.3 應力路徑對孔壓發展模式的影響

動三軸試驗得到的歸一化孔壓u/uf和歸一化振次N/Nf的關系曲線如圖5所示。uf是破壞時的孔壓，Nf是液化周次，N和u分別是振動周次和孔壓。結果表明，盡管不同動剪應力比下孔壓量值隨加載周次的增加幅度不同，但歸一化后曲線范圍相對狹窄，有較好的規律性。這和張建民等[8]的研究一致，他們認為歸一化孔壓與動應力大小無關，并給出了u/uf和N/Nf的擬合公式形式。動扭剪的試驗結果也有相似的規律，如圖6所示。但圓耦合的動孔壓擬合曲線則有所不同，如圖7所示，動剪應力比孔壓的影響較大，這表明主應力軸方向旋轉引起的力學效應不容忽略。

圖5 動三軸孔壓歸一化曲線

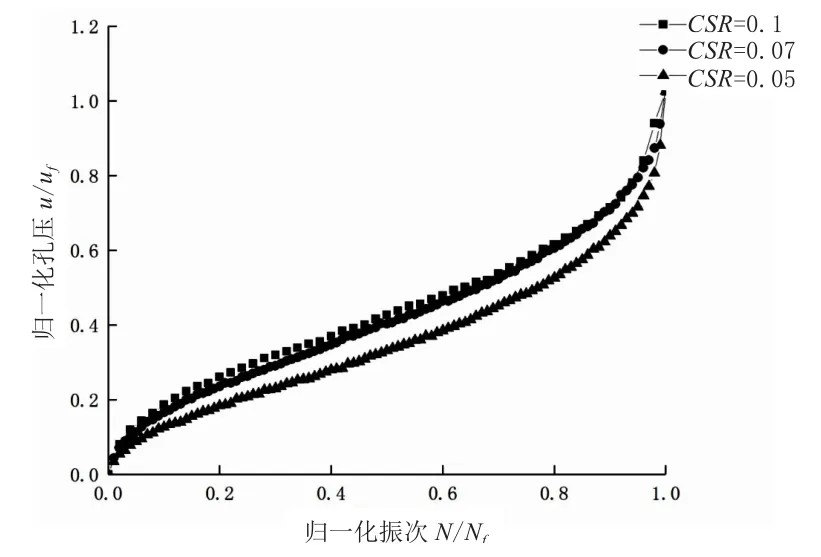
圖6 動扭矩孔壓歸一化曲線

圖7 圓耦合孔壓歸一化曲線

3 結論

文章采用空心圓柱扭剪儀，考慮不同的動剪應力水平，研究了中砂和松砂在不同加載方式下的抗液化能力，主要結論如下：（1）不同加載方式在砂土中引起的超靜孔隙水壓力增長速度有所區別，波浪荷載對應的圓耦合路徑下的發展速度最快，循環扭剪次之，循環三軸中最慢。（2）與孔壓發展規律對應，某一加載周數下，圓耦合試驗中達到液化破壞所需要的動應力水平最小，其與應力主軸旋轉引起的塑性體積應變有關。（3）循環應力比大小對動三軸和動扭剪應力路徑的歸一化孔壓發展模式影響不大，但對圓形應力路徑影響較明顯。