帶電粒子在偏轉電場運動過程中的能量轉化與守恒分析

陳 曦

(中國人民大學附屬中學 北京 100080)

張石友 張曉琳

(北京市第一七一中學 北京 100013)

在帶領學生進行高三復習時，遇到了一道看似平常的練習題，“奇怪”的是：從兩個不同的角度求解，得到的“答案”卻不同，引發了我們的思考與討論，問題描述如下.

【例題】兩個平行且彼此靠近的金屬板與一直流電源兩極相連，電源的內阻可忽略不計，兩板間形成的電場可認為是勻強電場.有質量為m，電荷量為-q的粒子，不間斷地從兩平行板左側中點以初速度v0沿垂直場強的方向射入電場，粒子偏轉后恰打在下極板的邊緣上，如圖1所示.已知單位時間入射的粒子數為n，兩平行板的間距為d，金屬板長度為L，不計粒子重力.求穩定時電源的輸出功率.

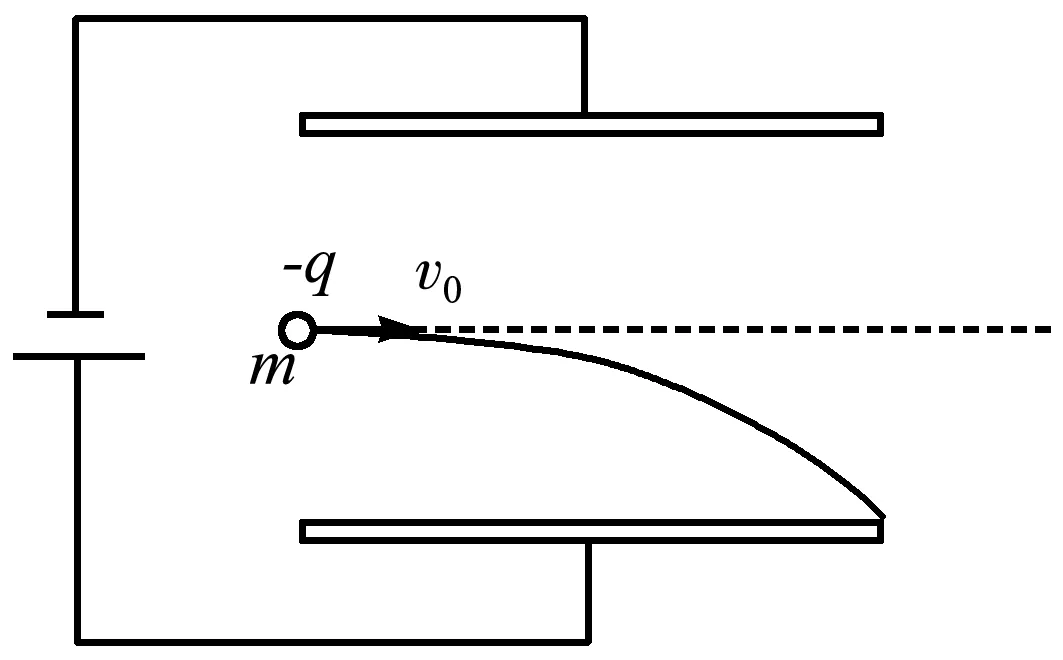
圖1 單個粒子打在極板的邊緣

解法1(參考答案)：

解析：粒子打在極板上，電路導通，電流

(1)

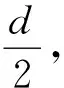
(2)

由式(1)、(2)，可得電源輸出功率

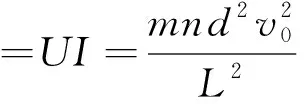
解法2(從能量轉化與守恒的大思路來展開)：

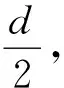
(3)

對單個粒子來說，電源做的功即增加的動能為

(4)

單位時間內電源對粒子所做的功，為

W=nW0

(5)

由式(3)、(4)、(5)，可得電源輸出的功率

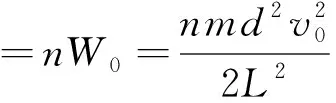
上述兩種方法中，一個認為回路中的電流是因為有帶電粒子打到極板上產生的；另一個則是避開電流的問題，直接利用能量守恒求解.孰對孰錯？

為了弄清楚這個問題，我們不妨做個假設：假如沒有帶電粒子打到極板上，如圖2所示.按照“參考答案”所給思路，電路中就會沒有電流，電源的輸出功率也將是零，那么帶電粒子偏轉后獲得的動能哪里來的？豈不違背能量守恒定律嘛！據此我們可以判定，第一種求解方法應該是存在問題的.

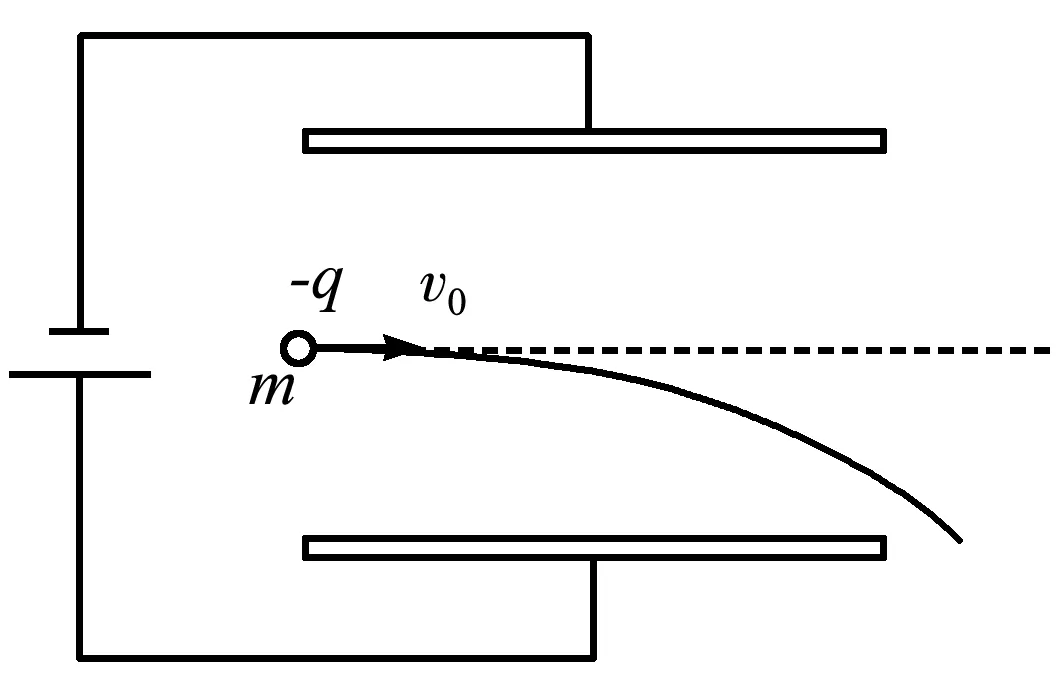
圖2 單個粒子從極板間射出

經查閱資料并討論交流后發現：帶電粒子(-q)在進入平行板電容器后會引起兩板發生靜電感應現象，在上下兩個極板上都感應出電荷，感應電荷的電量和帶電粒子與極板的距離有關.偏轉過程中，帶電粒子和兩個極板的距離發生變化，導致兩個極板上感應電荷的電量也發生變化.一部分感應電荷沿著外電路從一個極板流向另一個極板，形成電流.因此我們并不能認為只有帶電粒子打到極板上一瞬間，外電路中才會有電流，更不能認為電流的大小等于單位時間內打到極板上的電荷量.電流流過電源時，電動勢做功將其他形式的能轉化為電能和帶電粒子的動能.

為了能在高中或者高中物理競賽的知識范圍內計算感應電荷的電荷量，我們做以下兩個近似.第一，帶電粒子入射之前，只有兩極板之間存在勻強電場，空間其他位置處沒有電場.第二，入射帶電粒子的電量遠小于電容器所帶電量，帶電粒子入射之后，除帶電粒子周圍，兩極板之間的大部分區域內的電場仍然可以近似看作勻強電場.在這兩個近似下，我們能得到兩個結論.首先，利用高斯定理可以證明兩個極板上產生的感應電荷總量保持為+q.其次，利用電勢疊加[1]和高斯定理[2]，可以證明兩極板上感應電荷的電量之比等于兩極板和帶電粒子距離的反比.篇幅所限，我們將在后續的論文中進一步討論計算感應電荷的方法，并證明上述兩個結論.

具體舉例說明如下.

說明1：帶電粒子偏出電場

設單位時間內有n個帶電粒子進入偏轉電場并發生偏轉，如圖3所示.僅考慮進入電容器之間的帶電粒子引起兩極板發生靜電感應而產生感應電荷，整個“弧形帶電粒子流”在平行板電容器之間是穩定存在的，因此引起兩極板的感應電荷分布也是穩定的，因此只需考慮單位時間內“新進入”和“剛飛出”的帶電粒子即可，考慮到整個過程是持續穩定的過程，因此可以等效視為每1 s內都有-nq的電荷量進入,也有-nq的電荷“飛出”.事實上，為了弄清楚電路電流情況，我們只需考慮每秒內兩極板上因上述“飛入”和“飛出”的-nq電荷量引起的極板上感應電荷量變化即可，這個過程中電源負責搬運的電荷量也恰好是這個數值，這個電荷量與電路中的電流相對應.

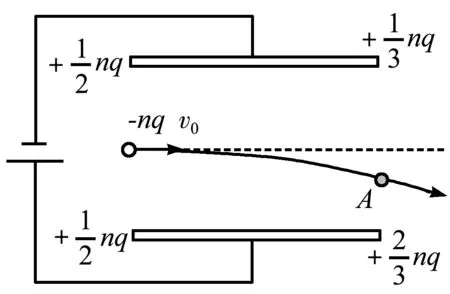
圖3 多個粒子從極板間射出

上極板感應電荷量變化為

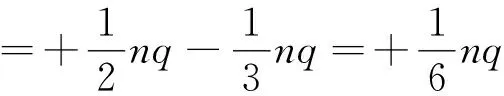
下極板感應電荷量變化為

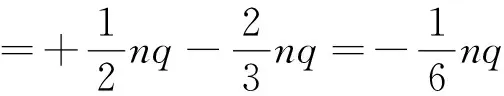
如果要維持系統穩定，極板上的電荷量應穩定不變，這就需要電源把上極板多出的電荷搬運到下極板.即：回路中的電流大小為

說明2：粒子未偏出電場，最終打在下極板上

我們回到初始的題目，帶電粒子恰好打到下極板邊緣(圖4).若帶電粒子打在極板上作為末態.沿用上述說明1中的思路，可以得出下面的結論：

這里面要注意每秒內打在下極板的電荷量-nq會使得下極板電荷變化，同時因這部分電荷打在了下極板而使上極板上的感應電荷消失.這樣總的來看：

上極板每秒內感應電荷量增加為

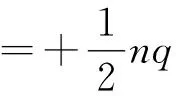
下極板感應電荷量增加量與打在下極板引起電荷變化的總和為

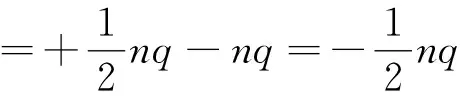
按照上述理論，回路中的電流大小應為

電源的輸出功率為

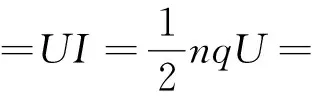
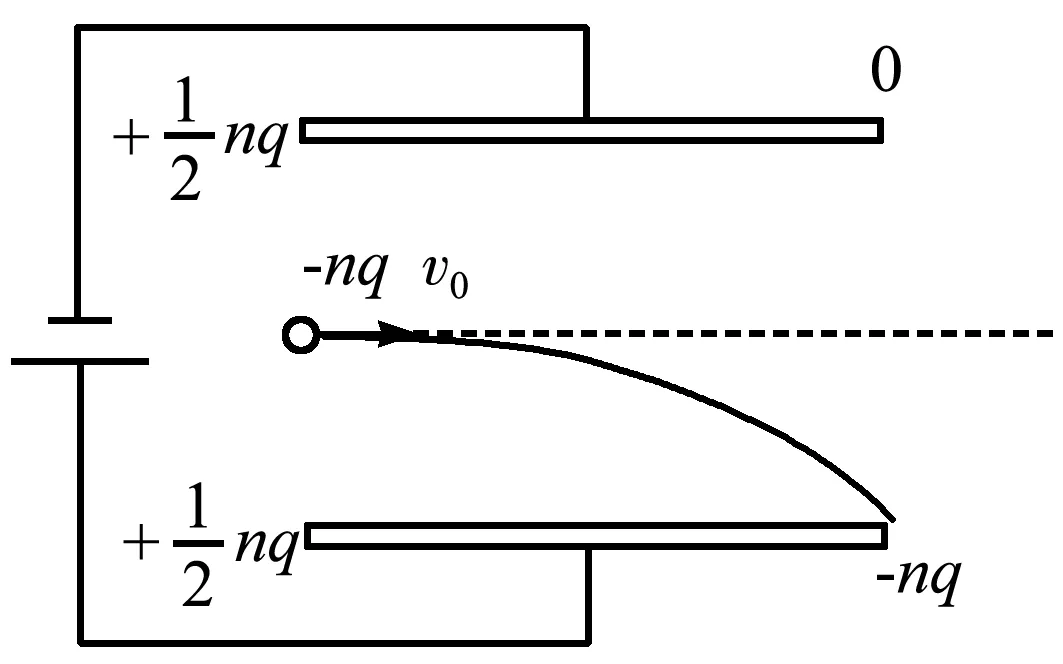
圖4 多個粒子打在下極板邊緣

當然了，盡管這種算法也能得到答案，但是筆者依然建議從能量轉化與守恒的角度來分析問題.

綜上所述，問題核心在于由于進入平行板電容器的并不是“等離子體”，這樣使得通過電路的電荷量不是打在極板上的“電荷”量.在帶電粒子不斷靠近極板時，極板上感應電荷發生變化，為形成穩定的狀態，電源會不間斷地把多出的電荷從一個極板挪到另一個極板上，從而在回路中形成電流.

但也要注意到，上面的討論也存在一定的局限性.考慮這樣一種情況：電容器兩極板帶等量異號的電荷，和電源斷開，如圖5所示.帶電粒子沿著虛線方向從無窮遠處射入電容器，偏轉之后離開電容器再運動至無窮遠處.這個系統的能量包含3部分，帶電粒子的電勢能、電容器的電勢能和帶電粒子的動能.帶電粒子從無窮遠處來，又運動到無窮遠處，它的電勢能不變.電容器的電荷量不變，電勢能也不變.帶電粒子在電容器中被偏轉電壓加速，動能增加.綜上所述，系統的總能量是增加的.在沒有電源供電的情況下，系統增加的那部分能量是從哪里來呢？是否能量不守恒了呢？

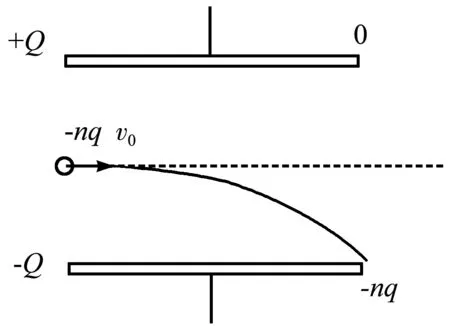
圖5 多個粒子的電偏轉

實際上，“忽略邊緣效應”這一錯誤近似導致了“能量不守恒”這一似是而非的結果.高中階段，我們通常認為只有電容器的兩極板之間存在電場.而實際情況是，為了保證靜電場做功和路徑無關，電容器的外部也必然存在電場，我們將這種現象稱為邊緣效應.帶電粒子穿過電容器兩極板之間時被電場力加速，電勢能轉化為動能；帶電粒子穿出電容器后，邊緣效應又會對帶電粒子減速，使其動能又重新轉化為電勢能.當帶電粒子回到無窮遠處時，它的動能和電勢能都會回到其從無窮遠出發時的數值，系統總能量守恒.

這些例子告訴我們，在高中物理范圍內分析帶電粒子在電場中的偏轉時，模型本身的局限性可能會導致某些荒謬的結論.在日常教學中應加以重視，引導學生們通過推理論證，認識物理模型的局限性，加深對能量、運動與相互作用等物理觀念的理解.