基于雙哈希模糊布隆濾波器云存儲數據融合
洪文圳,李冬睿,沈 陽
(1.廣東農工商職業技術學院 計算機學院,廣東 廣州 510507; 2.華南理工大學 軟件學院,廣東 廣州 510641)
0 引 言
工業物聯網(IIoT)在各領域的應用越來越多,IIoT連接傳感器和執行器快速大量生成異構數據[1,2]。當前面臨挑戰是高效和安全地存儲和處理/分析大量數據,特別是敏感IIoT數據[3,4]。此外,流式數據可能是短暫的,因此需要能夠在一次傳輸中對此類數據進行及時的分析和處理[5]。
當前已有許多針對IIoT數據的處理方法,例如,熊等。文獻[6]設計了一種近似的基于Bloom濾波器的密鑰值(k-v)存儲方法。文獻[7]提出一種動態Bloom濾波器數組,用于云存儲系統中成員身份的有效表示。文獻[8]提出可調節Bloom過濾器,稱為Scalable Bloom濾波器(SBF),通過添加新的過濾器來執行批量數據的插入,并且在兩個不同級別上執行查詢處理以提高其準確性和查詢復雜度。文獻[9]提出基于SDN的大數據管理方法來優化多云DT中的網絡資源消耗,Bloom濾波器被用來分析他們提出的解決方案的性能。Bloom濾波器在各個領域廣泛應用,可有效地處理可擴展性問題,缺點是查詢復雜度隨著輸入數據量增加而增加。
本文提出一種在確保失效數據魯棒性條件下,將兩個Bloom濾波器壓縮成一個濾波器的新方法,可更為有效利用存儲容量:①使用模糊交叉操作壓縮合并兩個Bloom濾波器,大量元素被容納在m大小Bloom濾波器中;②數據緩慢衰減,允許流數據在內存中駐留相當長的時間;③在不損失精度的情況下高效優化利用存儲空間。
1 數據存儲系統模型描述
1.1 IIoT網絡結構模型
圖1描繪了包括不同層的典型IIoT網絡結構設置,這些層結構的主要作用是信息獲取、計算、存儲和檢索。在初始階段,從地理分布的傳感器和執行器獲取異構數據。然后,通過IIoT和Internet基礎設施將收集的數據傳送到地理上分布的云DCs中,在那里存儲和深入分析數據。數據分析的結果隨后提供給授權用戶(例如,通過移動設備)。

圖1 IIoT環境下的數據存儲
典型的IIoT環境中的數據存儲包含以下兩個階段:①數據從連接設備、傳感器以及執行器進行發送;②一旦收到數據,對其進行濾波以去除異常和冗余值,并將過濾后的數據保存在內存中,直到在主內存中找到足夠存儲空間。與數據存儲相關的重要任務是明確數據壓縮(例如,在不影響其準確性的情況下,將減少的數據保存在較小的內存空間中)。目的是研究數據壓縮,以確保有效地利用可用的存儲空間進行大規模數據存儲。
1.2 Bloom濾波器

fp≈(1-e-kn/m)k
(1)
假陽性率可能隨著Bloom濾波器中潛在的插入過程而增加。然而,Bloom濾波器固有的節省空間的能力,往往克服了這一缺點。
1.3 問題描述
給定具有n個元素的數據流(Ds),即Ds={x1,x2,…,xn},主要要求是在存儲器和搜索復雜度方面改進現有的Bloom濾波器的性能。所設計結構可表示為如下問題[13]:
(1)流數據在很短時間內是可用的,因此必須一次性處理,并在內存中保留足夠長時間以便查詢。
(2)與散列相關的計算成本(Cc)應最小化。
(3)處理動態數據集時的查詢復雜性(Qc)應得到優化。
(4)用于存儲數據的存儲器應以最大數量的元素可容納的方式進行優化(Ea)。
(5)假陽性(fp),Bloom濾波器的重要性能參數不應超過預定限值。
上述問題可表示為如下數學模型
(2)
2 模糊交叉Bloom濾波器(FFBF)
2.1 模糊交叉操作
模糊交叉操作[14],首先合并ax∈BFi[]和by∈BFj[]的元素,其中x=y。這兩個元素在兩部分中具有相同的索引,彼此重疊并在上半部分存儲為單個模糊值。在此過程中,指紋位用于數據壓縮。融合的兩個Bloom濾波器,BFi[]和BFj[],被稱為第一交叉或第一壓縮形式。它由符號CRi,j表示,并且需要兩個位(塊位和指紋位)來表示使用模糊符號存儲在其中的元素。模糊交叉操作表示為⊙,并表示為如下模型
(3)


圖2 模糊交叉過程


表1 模糊操作
初始階段數據m/2,m/4,m/8,…可以壓縮形式查詢。簡單Bloom濾波器的主要特點是具有幾乎立即衰減率,FFBF與之相比具有相對較慢的衰減過程。FFBF中采用的交叉操作的計算成本幾乎可忽略,因為它僅對二進制集應用簡單的模糊操作。此外,當m取值較小時,所提模糊交叉操作在計算上變得低效。在這種情況下,通過將所有比特位設置為零可獲得相對更高的計算效率。
定理1模糊交叉運算不可交換,即
(BFi[]⊙BFj[])≠(BFj[]⊙BFi[])
(4)
證明:在FFBF算法中,Bloom濾波器的位置在交叉操作中起著重要作用。根據式(3),CR1,2是指BF1和BF2的壓縮形式。CR1,2中元素qy的查詢過程表示如下
(5)
因此,在模糊操作中Bloom濾波器的位置發生變化,搜索結果將受到重大影響。可以得出結論,模糊交叉運算不可交換
CR1,2≠CR2,1
(BFi[]⊙BFj[])≠(BFj[]⊙BFi[])
(6)
對于上述引理,得出結論如下:在模糊交叉運算中,α和β是互補的,而γ獨立于Bloom濾波器的位置。
定理2對于具有m和k哈希函數數組的給定Bloom濾波器,由FFBF容納的元素數(NFFBF)是簡單Bloom濾波器(SBF)容納的元素數(NSBF)的1.9倍
NFFBF≈1.9×(NSBF)
(7)

(8)
總迭代次數k由b個塊表示,如下所示
(9)
對于給定的m大小的Bloom濾波器,與SBE相比FFBF中可用的總內存(MFFBF)可計算如下
(10)
(11)
假設n個元素可由使用m大小Bloom濾波器的SBF容納。在相同大小數組中,FFBF可容納的元素總數如下所示
(12)

(13)
定理3CRi,i+1壓縮表示的假陽性率(FPCR)等于BFi[]和BFi+1[]的假陽性率(即FPi和FPi+1)
(14)
證明:模糊折疊是一種算術運算,CRi,i+1中的單個元素(即,來自BFi[]和BFi+1[]的個數)用模糊符號α,β,γ表示。每個符號都有唯一的簽名,見表1。例如,BFj[]中α表示1,而在BFj[]中α表示0。CRi,i+1的誤差主要來自于BFi[]和BFi+1[]中的突變位。但是,使用模糊符號不會導致CRi,i+1出現誤差。
(15)
因此,壓縮表示的假陽性率與具有參數m和k的SBF假陽性率相同。
2.2 FFBF中的數據插入

gi(x)={h1(x)+i×h2(x)}modmp
(16)
在上面公式中,mp是相對于BF(m)大小的最大限制范圍(1:m)和最接近素數(減少沖突次數)之間的散列函數的值。mp的選擇采取可生成最佳散列值方式進行選取。插入首先將m大小的數組劃分為兩個相同大小的Bloom濾波器
(17)
最初,元素被添加到第i個Bloom濾波器中。然而,當BFi[]的填充容量超過閾值填充比(Fthres)時,插入從BFi+1[]開始。在插入的第一級,根據以下散列值,只有塊位被設置為1
(18)
一旦達到BFi+1[]濾波器的閾值,模糊交叉操作⊙被應用在兩個濾波器(BFi[]和BFi+1[])上,以便在現有的Bloom濾波器中為更多的數據存儲空間。為使模糊交叉操作有效,m和k應該是2的倍數(即,表示為2x)。具體計算過程見算法1所示。
算法1:FFBF中的數據插入過程
輸入:數據流(S)
輸出:Bloom濾波器操作—插入&&折疊
(1) 設置S(Bloom濾波器的數據集);
(2) 設置m←Bloom濾波器的大小;
(3) 設置k←哈希函數(2x);
(4) 設置i←1;
(5) 設置BF[i]←Size(1,m/2);
(6) 設置BF[i+1]←Size(m/2+1,m);
(7) forx∈Sdo
(8) ifm≥kdo
(9) if FillRatio(BFi[])>Fthresthen
(10) if FillRatio(BFi+1[])>Fthresthen

(12)BFi[]←Size(1,m/2);BFi+1[]←Size(m/2+1,m);
(13) endif
(14) else


(17) endfor
(18) end
(19) endif
(20) else

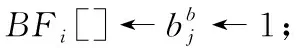
(23) endfor
(24) end
(25) endif
(26) else
(27) 達到最大插入極限;
(28) end
(29) end
2.3 FFBF中的數據查詢
FFBF中的查詢過程與標準Bloom濾波器的相同,這表明查詢的數據最初是散列的,Bloom濾波器中的相應位置被掃描以獲取HIGH位。在FFBF中,查詢過程始終從活動時隙A開始。如果在第A個時隙中找到元素,則查詢過程返回TRUE;否則,掃描將繼續,直到A=1搜索開始,按如下散列查詢方式
(19)

(20)
下面是根據上面定義的hResult()函數得出的結論
(21)
根據以上討論可得,查詢CR中的一個項目(y∈Q)的時間復雜度是O(k),如果CRi,i+1表示時隙BF[i]和BF[i+1]的2n個元素。算法2描述了上述FFBF中使用的整個查詢過程。
算法2:FFBF中的數據查詢過程
輸入:數據流(S)
輸出:Bloom濾波器操作—插入&&折疊
(1) 設置a←insertion(i);
(2) whilea≠0 do
(3) ifa→(BF[a]) then

(5)y∈BF[a]th;
(6) endif
(7) endif
(8) else ifa→(CRa-1,a) then
(9) Update(Cα,Cβ,Cγ)←hResult(y);

(11) endif
(12) if memPa==1 then
(13)y∈BFa-1[]th;
(14) endif
(15) else if memPa-1==1&&memPa==1 then
(16)y∈BFa[]th&&BFa-1[]th;
(17) end
(18) endif
(19)a=a-1;
(20) end
(21)y?S;
3 實驗分析
為實現對所提云存儲數據融合算法的性能測試,本實驗選取PBC 0.5.15測試庫進行模擬測試,可實現對文件失效情況下的批量審計模型設計,同時選取文獻[13-15]這3種云存儲算法進行對比實驗,該測試系統選取的開發語言是C語言。測試系統平臺軟件選取Linux 3.8.0-29,處理器配置為CPU Intel(R) E5605@2.55 GHz,系統內存大小是32 GB,系統硬盤是1 TB希捷機械硬盤。
設置云存儲過程中的數據塊大小是|id|=50 b,云存儲過程的測試文件大小為1 GB,設定模擬測試過程中的文件損壞的最大比例是1%,選取所有數據塊中的500組作為模擬對象進行數據審計。實驗對比指標首先選取云存儲過程中的通信數據開銷進行實驗對比,為確保測試過程所得結果穩定,每組實驗單獨運行30次求取實驗結果的均值進行對比測試。表2為本文算法與選取的3種對比算法的實驗對比結果。

表2 通信開銷測試數據對比
根據表2實驗數據可知,在算法的通信開銷指標上,本文所提的云存儲數據融合算法相對于選取的文獻[13-15]這3種云存儲對比算法具有較為顯著的性能優勢。隨著文件數量的增加,數據云存儲過程的通信開銷均逐漸增加,并且本文算法相對于選取的對比算法的通信開銷優勢逐漸增加,上述實驗結果驗證了所提算法在云存儲數據通信開銷指標上的性能優勢。
首先,利用本文算法與最差設定實驗情形進行對比實驗,即失效文件多數是成對出現。圖3為最差情形下,批量審計次數指標隨失效文件個數變化對比情況,模擬測試過程中設置文件總個數是256個。

圖3 批量審計次數實驗對比(最差)
根據圖3結果可知,在最不理想情況下,對于選取的幾種對比實驗算法中,本文算法的批量審計次數最少,這表明所提算法在給定失效文件情況下,所需要的失效文件審計指標最佳。對比算法中,文獻[13]算法因為需要對失效文件交叉內容進行重復性質的查詢操作,因此其在失效文件審計指標上要高于文獻[14]算法,表明其針對失效數據的處理能力要弱于文獻[14]算法。文獻[15]算法設計了一種快速識別算法,但是在最差實驗環境下,失效文件往往多數是成對出現的,這種實驗環境下,無法有效發揮文獻[15]算法快速識別過程的有效性,因此在實驗結果上的表現就是文獻[15]算法的批量審計指標雖然要優于文獻[13,14]算法,但是與本文算法相比仍有較大的差距。
其次,為了對上述情況進行對比分析,選取隨機情況再次進行實驗模擬,對比算法仍然選取文獻[13-15]這3種算法,實驗對比結果如圖4所示,模擬測試過程中設置文件總個數仍是256個。

圖4 批量審計次數實驗對比(隨機)
根據圖4結果可知,在隨機情況下,對于選取的幾種對比實驗算法中的本文算法的批量審計次數仍然最少,這與最差情形下的實驗結果一致,表明本文算法具有更廣的適應性。同樣,與最差情形相似,對比算法中文獻[13]算法因為需要對失效文件交叉內容進行重復性質的查詢操作,因此其在失效文件審計指標上要高于文獻[14]算法。由于設定為隨機實驗情形,因此文獻[15]算法設計的快速識別過程具有一定的效果,與本文算法實驗結果具有相對的接近性。
對于選取的256個模擬測試過程的總文件個數,設定其中失效的文件總數是17個,這些失效文件仍然采取隨機方式進行分布設置。對比算法仍然選取文獻[13-15]這3種算法,實驗指標選取查詢時間,單位是ms,實驗結果如圖5所示。

圖5 查詢時間對比
根據圖5所示實驗結果,文獻[13]算法因為需要在查詢過程中首先對測試數據的行列數據進行審計定位,因此其在查詢時間上相對于選取的對比算法具有更高的查詢時間。對于少量文件損壞情形,因為文獻[15]算法選取的是一種冪指查詢方式,因此其數據查詢時間相對較快,但是在文件損壞數量增加后,算法的查詢時間逐漸增加,并且查詢時間的增加幅度要顯著高于本文算法。文獻[14]算法查詢時間指標介于文獻[13]和文獻[15]兩種算法之間。根據上述時間結果可知,本文算法在查詢時間指標上也要優于選取的對比算法,體現了所提算法的性能優勢。
4 結束語
本文提出的濾波器采用一種模糊技術來解決Bloom濾波器的空間需求問題。我們驗證了所提出的方法可以在同一空間容納更多的元素。與SBF相比,由于所提出的濾波器僅包含二元集合上的簡單模糊運算,因此交叉和與之相關的運算的代價幾乎可以忽略不計。壓縮后的誤報率與標準Bloom濾波器相同。由于使用了雙哈希技術,兩個哈希函數生成k個哈希函數,因此哈希運算的計算時間也大大減少。FFBF的查詢復雜度取決于Bloom濾波器被劃分的塊的數量。從m大小的Bloom濾波器和相同大小的壓縮表示中搜索元素保持不變。實驗結果驗證了所提算法有效性。下一步,①對雙哈希模糊交叉Bloom濾波器進行進一步改進,提高算法計算效率;②考慮引入稀疏數據表示方式,對算法執行效率進一步改進提升;③考慮實際應用軟件開發,驗證真實環境算法性能。

