楊房溝拱壩電梯井結構配筋研究

葉 甜， 王 鴿， 戴 永 琪， 么 倫 強， 陸 高 明

(1.中國電建集團華東勘測設計研究院有限公司，浙江 杭州 311122；2. 雅礱江流域水電開發有限公司，四川 成都 610000 ； 3.河海大學，江蘇 南京 210024)

0 引 言

拱壩可以借助拱的作用將壩前水壓力全部或部分傳遞給兩岸山體，在地質條件滿足要求的情況下，拱壩比重力壩和當地材料壩更具經濟性和安全性。本世紀以來，中國建設了多座高拱壩，如構皮灘水電站、拉西瓦水電站、溪洛渡水電站、小灣水電站的大壩壩高均超過了200 m，錦屏一級水電站的拱壩壩高高達305 m。電站運行需要對大壩進行日常管理和維護，高拱壩的廊道高程范圍大，通過設置電梯可以大幅度減少通行時間。通常采用在拱壩內部預留相關井道形成電梯井，因此，電梯井周邊混凝土將產生應力集中現象，需要利用配筋加以解決。

1 工程概況

楊房溝水電站是我國首個以EPC模式建設的百萬千瓦級大型水電工程，水電站位于四川省涼山彝族自治州木里縣境內的雅礱江中游河段上，是規劃中該河段的第6級水電站，工程的開發任務為發電。水庫總庫容為5.125億m3，總裝機容量為1 500 MW，楊房溝水電站為一等工程，工程規模為大(1)型。樞紐主要建筑物由擋水建筑物、泄洪消能建筑物及引水發電系統等組成，主要水工建筑物為1級建筑物。

擋水建筑物采用拋物線型混凝土雙曲拱壩，最大壩高155 m，河床建基面高程1 947 m，壩頂高程2 102 m。拱壩內共布置2部電梯用作通行，分別為2 102～2 005 m高程電梯和2 005～1 955 m高程電梯，其中2 102～2 005 m高程電梯為高速電梯。筆者研究對象為2 102～2 005 m高程電梯對應的電梯井，電梯井按結構特征從上到下可分為電梯機房、電梯井、電梯緩沖坑。

2 有限元子模型法

首先進行整體計算，整體計算后可以得到子模型與整體模型接觸面上的節點位移。子結構取出之后，將接觸面上的節點位移作為約束條件加在脫離體上，加上其他荷載共同計算子模型應力[1-3]。子模型計算示意圖見圖1。

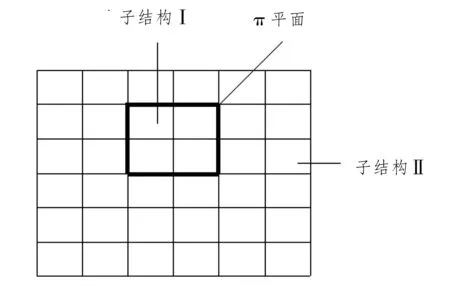
圖1 子模型計算示意圖

(1)子模型位移邊界。

整體計算時，按照一般的有限元計算方法，子結構Ⅰ、Ⅱ共同參與計算，得到Ⅰ、Ⅱ接觸面π上的節點位移時程。設π截面上的面單元節點數為m。每個節點在計算時段內在xyz坐標系下，某一時刻π截面上的節點位移分量為：

δi(t)={δXi(t)δYi(t)δZi(t)}

(1)

假設每個面單元內任意一點的位移由節點的位移分量通過單元形函數插值而得。

(2)

(3)

(4)

將子結構Ⅰ單獨取出并加密，π平面上的新增結點的位移通過面單元形函數由π平面上的已知結點位移插值得到。

(2) 子模型有限元計算方法。對于給定的結構體系，施加相應的約束邊界條件后的有限元方程為：

Kδ=F

(5)

式中K為結構剛度矩陣；δ為未知節點位移向量；F為荷載列陣。

對某一結構系統，若用給定的截面π將結構分為Ⅰ和Ⅱ兩個子結構，并對這兩個子結構在該指定截面上施加一組大小相等、方向相反的約束內力，則可建立與方程(5)完全等價的另一組方程[3]：

(6)

式中C為π截面上的節點；i為非π截面上的節點；Fi為非π截面上的節點荷載向量；Fc為π面上節點荷載向量；fc為π截面上Ⅰ，Ⅱ兩子結構間的約束內力。

初步計算和加密時得到截面π上的節點位移δc，對于子結構Ⅰ，方程(6)可以簡化為：

[kii]1{δi}={Fi}

(7)

按照一般有限元方法即可得到加密后子結構內部結點的位移，從而計算內部結點的應力。

3 電梯井配筋計算數值模擬

3.1 數值模型及巖土體參數取值

圖2為楊房溝水電站軸視圖，即拱壩整體計算模型；圖3為拱壩2 102 ～ 2 005 m高程電梯井子模型。首先對拱壩整體模型計算分析，得到電梯井子模型與大壩整體模型接觸面上的節點位移，將接觸面上的節點位移作為約束條件加在電梯井子模型上，加上其他荷載共同計算電梯井子模型應力。整體模型中，地基沿上壩面與建基面交線最低點往下取1.5倍壩高，壩前取2倍，壩后取3倍，大壩兩側取1倍壩高。整體有限元模型節點數為109 984，單元數為94 161。

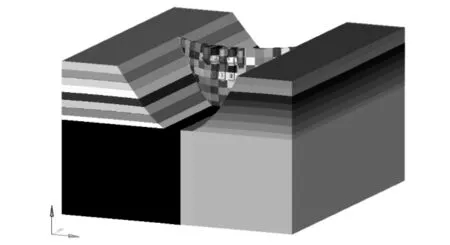
圖2 楊房溝水電站軸視圖

圖3 高程電梯井子模型

3.2 邊界條件

3.3 特征水位

楊房溝水電站水庫上、下游特征洪水位見表1。

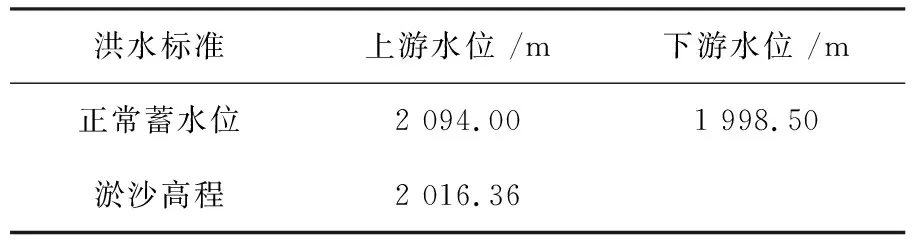
表1 水庫上、下游特征洪水位

3.4 材料參數

(1)淤沙參數。淤砂浮容重：0.5×103kg/m3；淤砂內摩擦角： 0°。

(2)壩體混凝土材料參數。拱壩主要采用C18030、C18025混凝土，閘墩和孔口部位采用C30混凝土，閘墩頸部及支撐大梁混凝土采用C40。拱壩壩體及閘墩混凝土材料物理力學參數見表2。

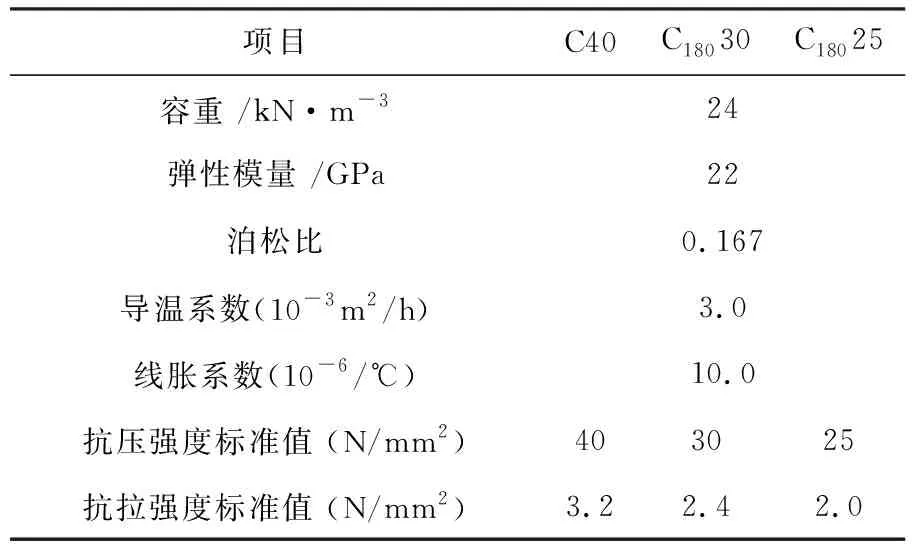
表2 拱壩壩體及閘墩混凝土材料物理力學參數

(3)鋼筋材料參數。結構鋼筋采用HRB400E鋼筋，抗拉強度設計值采用360 N/mm2，預應力閘墩處鋼絞線采用1×7類型，公稱直徑15.2 mm，抗拉強度標準值為1 860 N/mm2，抗拉強度設計值為1 320 N/mm2。

(4)分項系數。

結構重要性系數γ0=1.1；

荷載分項系數γQ=1.1；

結構系數γd=1.2；

結合新課程改革，樹立素質教育的新理念，尋找新教法，運用多媒體，培養學生具有正確迅速的運算能力，這就要求數學教師要培養學生扎實的基礎知識，敏銳的觀察能力，熟練掌握使用計算工具，熟記一些常用數據和劃法、算法、變形算法。按照正確的法則和最佳的方法把幾個數據式組成一個新的結果，結合變形能力，講好講活。除此之外，根據論證和運算的需要，加強字母表達運算能力的培養訓練，把數和式從一種表達形式轉換成另一種表達形式的分解變形能力。找新教法，運用多媒體，培養學生具有正確迅速的運算能力。

持久狀況系數為ψ=1.0。

(5)壩基材料參數。拱壩壩基綜合變模設計取值見表3。

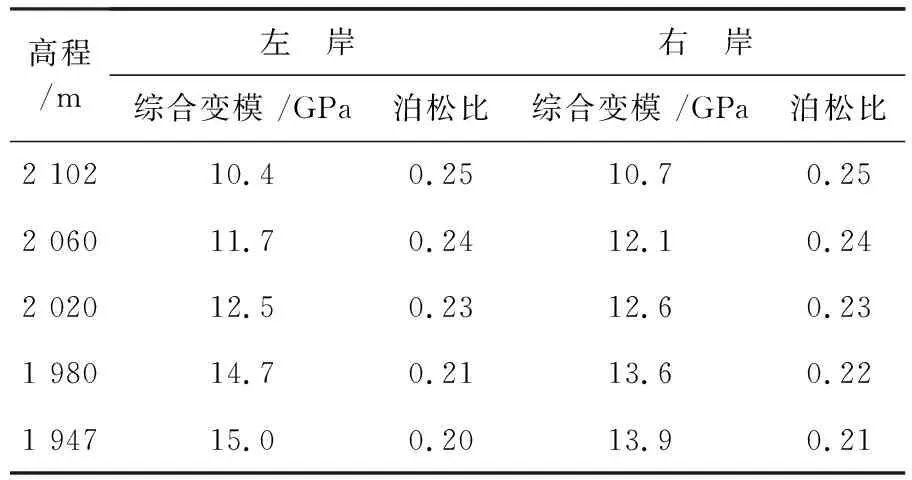
表3 拱壩壩基綜合變模設計取值

3.5 計算荷載

根據結構設計要求，所有荷載都按《水工建筑物荷載設計規范》[4]和《水工混凝土結構設計規范》[5]要求取荷載標準值計算。

(1)自 重。自重計算公式為：

Gi=γm×Vi

(8)

式中Gi為計算單元的自重(kN)；γm為計算單元混凝土重度(kN/m3)；Vi為計算單元的相應體積(m3)。

(2)靜水壓力。靜水壓力計算公式為：

Pwr=0.5×γ水×H2

(9)

式中γ水為水體的重度，計算中取γ水=10 kN/m3；H為作用水頭(m)。計算中全部靜水壓力按照分布面力施加在相應的作用面上。

(3)溫度荷載。拱壩各特征高程溫度荷載見表4。

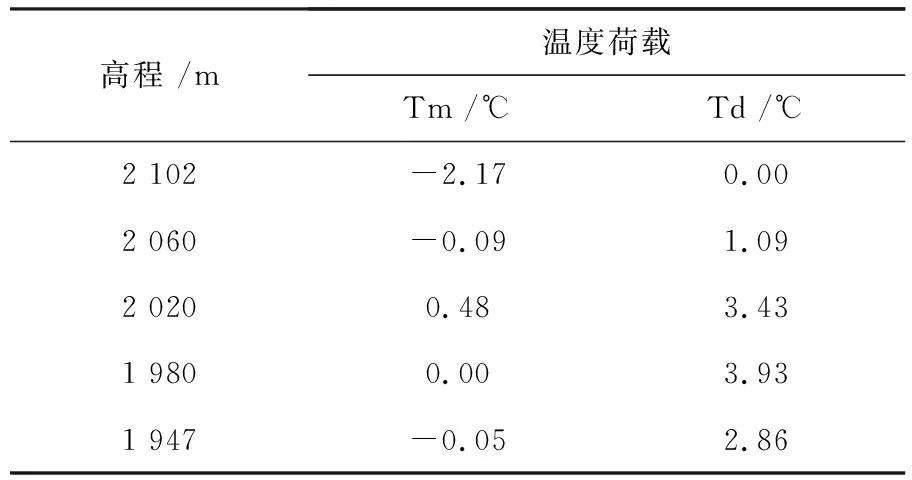
表4 拱壩各特征高程溫度荷載

3.6 計算工況

在有限元靜、動力計算中，主要考慮以下工況組合，見表5。

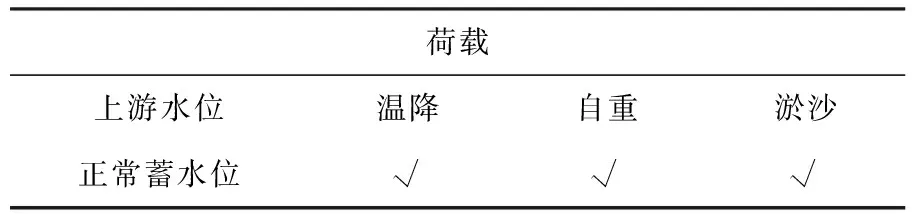
表5 工況組合表

4 配筋計算結果與分析

4.1 電梯井應力分析

靜力工況下電梯井子模型應力云圖見圖4。靜力工況下電梯井周邊混凝土應力峰值見表6。可以看出：(1)電梯井子模型主拉應力最大值為5.49 MPa，發生在電梯井底部。(2)電梯井子模型主壓應力最大值為20.80 MPa，發生在壩體底部下游側。

圖4 電梯井電梯井子模型應力云圖第一(左)第三(右)主應力(Pa)

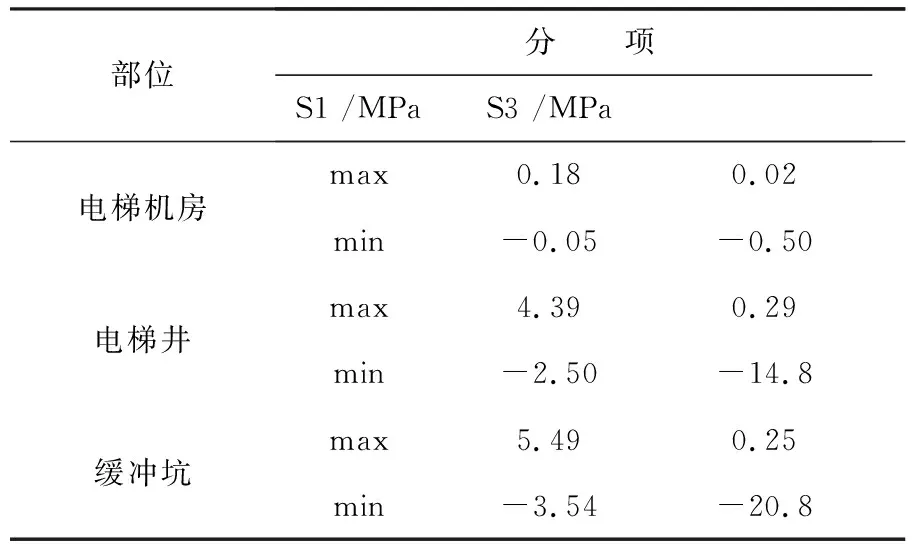
表6 靜力工況電梯井周邊混凝土應力峰值

4.2 電梯井配筋計算

根據電梯井各部位應力計算結果，采用混凝土承載能力極限狀態配筋[4-5]。截取相應的截面，并對截面切取適量的線，從而得到拉應力圖形，由混凝土結構的應力圖形進行承載能力極限狀態配筋計算，確定鋼筋用量[6]。

(1)電梯機房配筋計算。靜力工況下電梯機房的第一、三主應力分布情況見圖5、6。

圖5 靜力工況下電梯機房第一主應力(Pa)

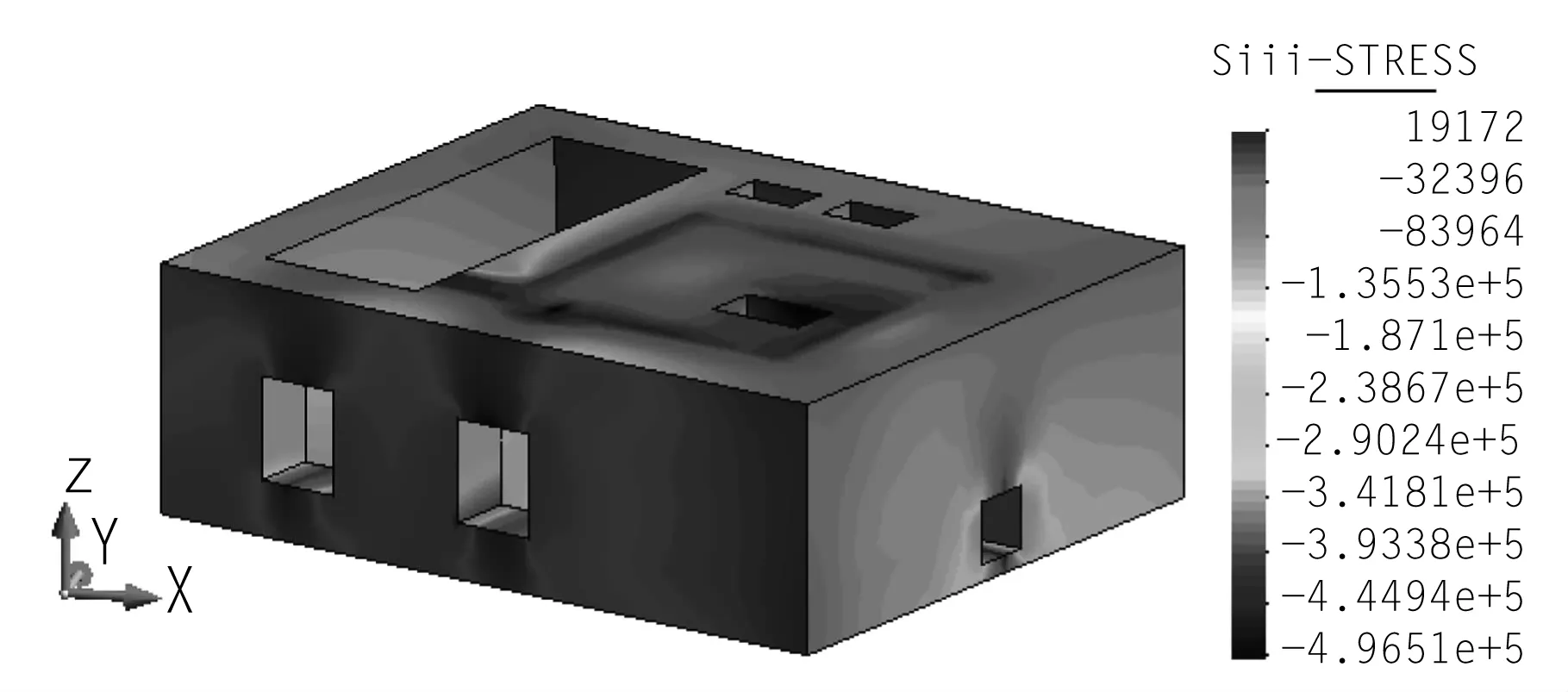
圖6 靜力工況下電梯機房第三主應力(Pa)

水平向控制應力為0.108 MPa，承載能力極限狀態下單位厚度最大配筋量為1 279 mm2。徑向控制應力為0.050 MPa，承載能力極限狀態下單位厚度最大配筋量為1 279 mm2。

(2)電梯井配筋計算。靜力工況下電梯井的第一、三主應力分布情況見圖7、8。

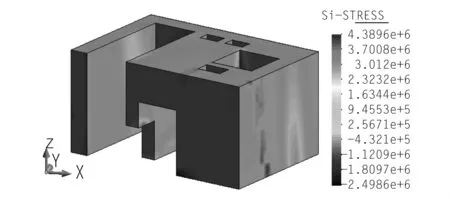
圖7 靜力工況下電梯井第一主應力(Pa)

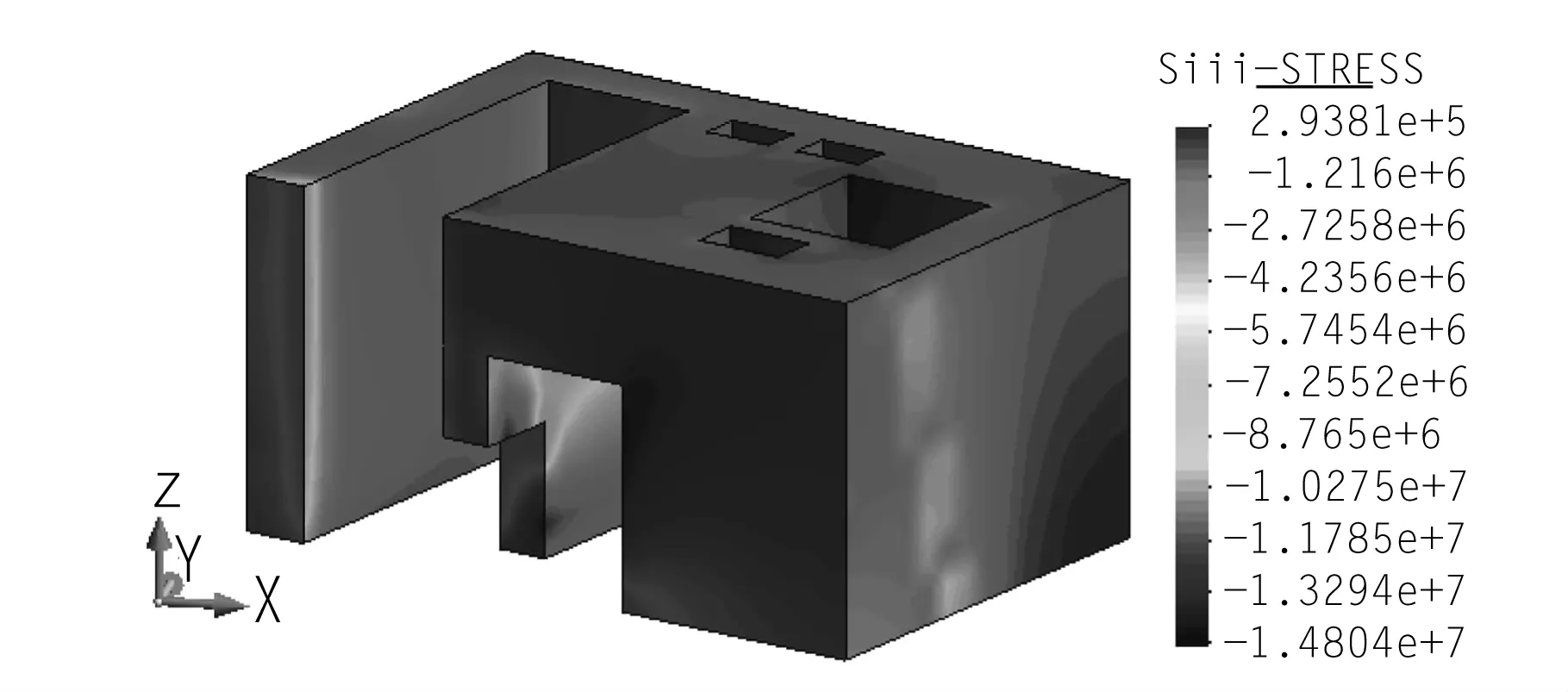
圖8 靜力工況下電梯井第三主應力(Pa)

水平向控制應力為0.343 MPa，承載能力極限狀態下單位厚度最大配筋量為480 mm2。徑向控制應力為0.619 MPa，承載能力極限狀態下單位厚度最大配筋量為4 176 mm2。

(3)電梯緩沖坑配筋計算。靜力工況下電梯緩沖坑的第一、三主應力分布情況見圖9、10。

圖9 靜力工況下電梯緩沖坑第一主應力(Pa)

圖10 靜力工況下電梯緩沖坑第三主應力(Pa)

水平向控制應力為0.817 MPa，承載能力極限狀態下單位厚度最大配筋量為5 996 mm2。徑向應力主要為壓應力，按構造配筋。

(4)配筋設計及其他工程配筋類比。根據本節(1)～(3)的靜力工況進行電梯井結構應力計算和配筋設計，并考慮留有50%以上的安全裕度，擬定電梯井配筋方案為：配筋直徑為28 mm、兩層、間排距為20 cm的配筋方案，相應單位寬度配筋面積為6 154.4 mm2。根據部分高拱壩電梯井配筋設計參數統計(表7)，楊房溝水電站電梯井配筋設計與同類工程類比，電梯井的配筋設計與國內同類混凝土高拱壩基本相當。

表7 部分高拱壩電梯井配筋設計參數統計表

5 結 語

采用有限單元數值分析方法，考慮自重、靜水壓力、淤沙壓力、溫度荷載的作用，對楊房溝2 102～2 005 m高程電梯井進行應力及配筋計算分析，并結合其他類似工程的設計經驗，擬定配筋方案。根據電梯機房、電梯井、電梯緩沖坑在靜力工況下的第一、三主應力分布情況，采用應力圖形法計算得到承載能力極限狀態下電梯井周邊混凝土單位厚度最大配筋量，結合工程類比確定電梯機房、電梯井、電梯緩沖坑的配筋方案。