應對水文序列非一致性變化影響的溯源重構法研究
秦 毅,李 時
(省部共建西北旱區生態水利國家重點實驗室西安理工大學,陜西西安 710048)
1 研究背景
近年來,大量研究成果表明實測水文序列存在明顯的非一致性特征[1-4]。它帶來兩方面問題:(1)在非一致性條件下,繼續使用以一致性樣本為基礎的預測分析方法,包括傳統水文頻率分析方法、多元統計分析的Coupla方法、機器學習等方法是否能獲得合理的成果,以及對未來的預測應該如何評價。(2)水文模型參數的率定工作變得困難,因為參數率定采用資料的非一致性導致了不確定性的增加。相比較而言,第一個問題在設計分析方面顯得更為突出,例如水利工程、水土保持工程及生態工程的設計,洪旱災害的防治等都離不開對實測樣本序列的統計分析與預測,除非研究對象的物理機制被真實地掌握,否則所做出的水文分析與預測的結果只有在一致性(平穩性)序列條件下才有意義。因此學者們投入了大量研究,包括:(1)對水文序列非一致性變異診斷的深入研究,給出了相對成熟的診斷方法:如相關系數檢驗法、Spearman秩次相關法、Kendall 秩次相關法、Mann-Kendall檢驗法[5-6]、R/S分析方法[7]、非參數Pettitt檢驗法[8]等。在此基礎上,謝平等[9]構建了水文變異診斷系統,更全面地反映了水文序列的變異特征。(2)解決非一致性條件下的頻率分析問題,這是工程設計迫切需要解決的問題[10]。為應對非一致性序列的影響,除了采用水文分析計算相關規范提出的還原或還現方法外,近年來有學者們將研究焦點放在了時變矩法[11-12]上,并據此建立時變概率分布,再通過重現期或可靠度與時變概率分布間的關系確定出工程設計值。當前比較有代表性的方法包括基于修正重現期的EWT[13-14]和ENE方法[15-16],和基于可靠度的ER[17]、DLL[18]和ADLL[19]等方法。
然而,這些方法仍然存在一定的爭議。首先是對趨勢的看法,有學者認為觀測到的水文序列的趨勢并非是非一致性特征的表現,而可能是平穩過程中的周期性頻率波動所致[20],甚至認為趨勢這個詞都缺少明確的定義[21];再者,實踐中,在工程設計壽命內,一定可靠度下的設計值將隨著計算時段的起始時間以及統計參數與協變量間關系擬合曲線的類型而變化,這就意味著未來設計值的可靠性嚴重依賴統計參數的時變特征,而這種時變特征卻因為時間序列遍歷性的缺失,造成對未來水文序列統計參數預測的不確定性[22]。正如Serinaldi等[23]指出的,如果模型結構無法通過演繹推斷的方式獲得,特別是描述分布參數非平穩變化模型是僅通過歸納推理擬合得來,則一個額外不確定性來源被無形中引入了模型結構中,使得所得到的非平穩模型無法在實際應用中提高設計值的可信度與準確性,而模型的這種不確定性將很容易導致不具物理意義的結果產生;此外,利用時變參數識別非平穩序列的分布函數過程中,所采用的經驗頻率計算方法也是引起不確定性的重要因素,因為計算經驗頻率的方法也同樣要求樣本為簡單隨機樣本,基于非平穩序列直接進行經驗頻率計算顯然不恰當。可見,對于統計特征隨時間變化的單一隨機變量,其分布研究尚存在如此多的問題,更何況解決多元時變隨機變量的聯合分布問題,難度可想而知。
很顯然,造成“難度”的核心是樣本序列的非簡單性。如果能夠將非一致性樣本序列轉換為一致性序列,則因為對此簡單序列已經有了成熟的分析理論、技術和用好技術的方法,前述困難將不復存在。因此,本文提出溯源重構法,它是基于反映水文現象物理機理的源函數將非一致性序列重構為新的一致性序列的方法。依靠重構的一致性序列,解決需要基于一致性序列才能進行分析工作的問題。事實上,當前已存在將非一致性序列轉變為一致性序列的方法,即還原或還現法、分解合成法,本文將在后面就這兩種方法與溯源重構法進行比較與討論。
2 溯源重構法的理論與方法
2.1 源函數的概念一般來說,一個水文變量Y的變化是多個影響因子X1,…,XN共同作用的結果,見圖1。在排除其他影響因子影響的條件下,單獨考察影響因子Xi對水文變量Y的作用,將這種作用規律記為fi(Xi),則fi(Xi)是Xi對Y的物理作用機制,因此這里稱fi(Xi)是Xi作用于Y的源函數。作為物理機制,源函數是不會改變的,就像河道流量Q=AV,其中A是過流斷面的面積,V是流速,則V和A各自對Q的作用規律或說機制,也即源函數就是fV(V)=V,fA(A)=A。當V或A或兩者共同隨時間變化時,流量也會隨著V(t)或A(t)或兩者在不同時刻的取值而表現出隨時間變化的Q(t)。但是,不論V和A怎樣取值,源函數fV(V)=V,fA(A)=A保持不變,而流量等于這兩個源函數相乘的機制也不會改變。即物理機制不隨時間變化,變化的永遠是Xi的狀態。

圖1 各影響因子對研究變量Y的源函數作用關系
嚴格的說,源函數的確定有兩種方法:理論推導(數學解析)和實驗分析。實際上,由于水文現象變化的復雜性,即便我們認可源函數的存在,也會因為人類對自然的有限認知而很難得到絕對準確的物理機制數學表達,至少當前很少看到對單一因子影響的研究。由于事物之間的作用規律可以隱含于統計規律中,所以當下可以借用Y和Xi間的統計關系來近似估計源函數。
既然源函數或由源函數構成的函數不隨時間變化,我們就可以利用這個特征將非一致性序列轉變為一致性序列。
2.2 溯源重構方法的基礎模型欲利用源函數時不變的特點,就要表達出多個影響因子各自對Y作用后的一般綜合關系。鑒于數學解析方法暫時行不通,故采用建立統計模型的方法來表征研究對象Y與解釋變量源函數之間的關系。眾所周知,數學的基本運算包括加(減)與乘(除),結合運算法則,Y與解釋變量源函數之間的關系有兩種一般性廣義表達方式,一是各解釋變量間相互獨立時采用的疊加模式:

另一個是可以考慮解釋變量間存在相關性的乘積模式:

其中:N指作用于研究變量Y的所有影響因子的個數,這些影響因子包括人類認識到的和尚未認識的;fi(Xi(t))為影響因子Xi的源函數。假設在N個影響因子中,有n個因子是人類目前已認識到的,它們的“源”函數分別為f1(X1(t)),…,fn(Xn(t));未知影響因子及其“源”函數分別為fn+1(Xn+1(t)),…,fN(XN(t))。則式(1)和式(2)改寫為:
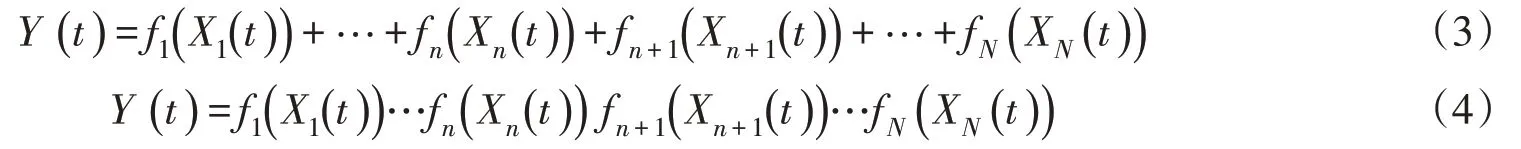
分別記δ=fn+1(Xn+1(t))+…+fN(XN(t))和δ*=fn+1(Xn+1(t))…fN(XN(t)),他們代表人類未知的影響因素對Y的作用,通常可以認為是自然隨機變量,具有概率分布,并具有對應的均值μ、μ*,和方差σ2、σ*2。令Ks(t)=f1(X1(t))+…+fn(Xn(t))和Kp(t)=f1(X1(t))…fn(Xn(t))。在生產實踐當中,由于我們更關心影響因子取給定值時,Y的變化情況,與回歸分析的考慮相同,在計算Y之前,解釋變量X1(t),…,Xn(t)的取值已經確定,可以作為可控變量處理[24]。于是Ks(t)和Kp(t)在t時刻為常數,故Ks(t)和Kp(t)是已知的時間函數。重新寫上述式(3)、式(4)為:

對比兩種表達式下Y(t)的條件數學期望和條件方差如下。
疊加模型:

乘積模型:

不難看到,兩種模型下Y(t)的條件均值均是時變函數,一旦Xi發生趨勢性變化,Y(t)的條件數學期望也就出現趨勢性變化;與均值不同,在疊加模型下的方差為常數,而乘積模型下方差是時變函數,且會隨Xi的趨勢性變化而產生更強的趨勢性。
現在來考察水文現象變化的普遍特點。水文現象是在水文系統內各要素間普遍存在相互影響的背景下發生的。各解釋變量間基本不存在絕對的獨立性,他們的相互作用使水文系統呈現出高度復雜的自適應非線性狀態。隨著近年來的環境變化,大量的研究成果表明不僅水文變量的量級表現出了非平穩變化,而且水文極端事件也急劇增多[25-26]。從統計的角度來看,這種現象表明了水文序列的一、二階矩均發生了變化[27-28],特別是極端事件的極端特性越強,二階矩的變化就越不能被忽視[29]。因此,可以得到結論,乘積模式相較于疊加模式更適用于描述具有復雜相關性的水文系統。故這里采用乘積模型(11)作為溯源重構法的基礎模型。

2.3 溯源重構函數與重構序列考慮到Y(t)的非一致性變化是因為解釋變量的非一致性變化引起,那么如果將所有帶有非一致性變化的影響因子的作用從Y(t)中剔除,見式(12),則剩余量將表現出一致性。

在式(12)中,m是非一致性變化的影響因子個數。其右端為Y(t)剔除全部非一致性因子影響后剩余一致性影響因子以及尚未被人類認知的影響因子源函數的乘積,它是平穩的隨機過程。如果只剔除了部分非一致性變化因子X1,X2,…,Xl(l 理論上,當引起Y非一致性變化的影響因子全部被識別出來,即l=m,且這些因子的源函數fi(Xi(t))已有準確的表達,那么由溯源重構函數計算出來的溯源重構序列RSt={rs1,rs2,…,rsn}為一致性序列,可用于需要一致性序列才能進行工作的情況。生產實踐中,因人類認知和現有方法的局限,我們不可能得到絕對的平穩過程,這也不是我們的目標,但隨著非一致性變化的解釋變量對應的正確源函數不斷加入溯源重構函數中,則溯源重構序列將逐漸趨向并最終趨向于平穩,接近于一個隨機噪聲。 需要提醒的是,由于估計源函數存在不確定性,所以使用中必須配合溯源重構序列RSt的一致性檢驗。若檢驗結果為一致,則同時接受所確定的影響因子及其源函數的估計形式,否則,仍需進一步研究影響因子及其源函數。 由于研究變量Y和影響因子間的因果關系,研究變量Y的各種非一致性變化(線性、非線性、突變)與影響因子的相應非一致性變化一致,這使得溯源重構法去除非一致性時并不受非一致性變化類型的影響,即具有普遍性。相較于對非一致性變化的Y進行純數學模擬的時變矩法,溯源重構方法更注重找到引起Y變化的非一致性變化影響因子Xi和它對Y的作用規律,并以此規律將非一致性變化從Y序列中排除,這正是溯源重構法能夠將非一致性變化的Y(t)變為一致性序列RS(t)的關鍵所在。 3.1 研究區域與數據利用陜西省榆林市佳蘆河流域申家彎水文站年最大洪峰系列資料作為實例研究,考察溯源重構法構建一致性序列的效果。由于溯源重構法的重點是依據非一致性變化影響因子對水文變量的作用(即源函數)來確定溯源重構函數的,因此在研究中,首先應研究確定非一致性變化的影響因子。實踐中,可以依據水文現象的相關理論知識并結合實地踏勘調研等手段,初步確定研究變量的主要影響因子,之后對這些主要影響因子進行趨勢分析,找出造成水文變量非一致性變化的影響因子。 佳蘆河位于黃河中游的河龍區間,毛烏素沙漠南緣,陜北黃土高原北段,屬于黃土高原溝壑區。河流由西北流向東南,至佳縣佳蘆鎮木廠灣村注入黃河。河流全長93 km,流域面積1134 km2,出口控制站為申家灣水文站。流域洪水由降雨引發。由于氣候較為干旱,自然條件較差,該地區容易發生風沙災害,水土流失現象普遍。為了控制水土流失,流域內修建了數十座淤地壩。淤地壩一般由兩大件組成——壩和泄洪臥管。為了使入庫泥沙得到沉積,實現多攔沙少攔水的功效,淤地壩運行方式設計成:發生洪水時,高含沙洪水首先被攔截在庫內,后由臥管分數天將洪水排出庫外,且要求臥管排水速度緩慢,排水流量一般為1~1.5 m3/s。結果導致出口斷面洪峰較建壩前明顯減小,庫壩泄流對流域出口的洪峰流量的貢獻可以忽略不計。這種效果等同于流域產生洪峰的產流面積減少,減少的數量為庫壩控制面積。這里稱流域面積與庫壩控制面積的差為有效產流面積;另一方面退耕還林以及淤地壩的蓄水,使得坡面較大范圍內的土壤含水率增加,促進了植被增長,導致流域植被截留、下滲、匯流等條件均發生改變,也造成了洪峰流量序列的非一致性變化。因此,選擇有效產流面積與植被覆蓋度作為佳蘆河流域年最大洪峰流量序列非一致性變化的主要影響因子。 洪峰流量序列采用申家灣水文站1957—2010年實測數據進行分析。1957—2010年有效產流面積序列則根據流域面積與逐年修建淤地壩的控制面積計算確定。植被覆蓋度(FVC)是利用landsat4-5 TM 30 m×30 m遙感資料,通過歸一化植被指數(NDVI)的分析計算得到[30]。由于植被覆蓋度序列長度受限于遙感資料的年限,僅有1988—2010年23年資料。但在1980年代前,流域人類活動影響較弱,且退耕還林等生態工程尚未起步,因此1980年代以前的植被狀態較為穩定,本文將1988年前的植被覆蓋度均取值為1988年數據。 圖2和圖3分別展示了佳蘆河流域出口斷面水文站申家灣站的年最大洪峰流量序列的變化和流域有效產流面積的變化。可以看到,流域洪峰流量和有效產流面積在1975年左右均發生了突變。圖4顯示了流域植被覆蓋度的變化情況。對各序列采用Pearson 相關系數檢驗判斷序列的線性趨勢,Spearman 秩相關系數檢驗判斷包括非線性趨勢在內的一階矩趨勢,采用Breusch-Pagan 檢驗[27]判斷二階矩的趨勢。因1988年前的植被覆蓋度數據為作者外延處理確定的,對植被覆蓋度趨勢性檢驗時采用1988—2010年的數據進行分析。由于淤地壩因逐年修建而增多,且建壩本身不屬于隨機事件,所以有效產流面積序列呈現顯著單調下降的趨勢,也沒有一般隨機序列的波動變化。 圖3 佳蘆河流域有效產流面積序列 圖4 佳蘆河流域植被覆蓋度序列 檢驗結果(表1)表明年最大洪峰流量序列的均值和方差都出現了顯著減少趨勢,但植被覆蓋度的均值出現顯著上升趨勢。由于年最大洪峰流量一般在汛期發生,本文對佳蘆河流域申家灣站的各時段致洪降雨序列進行了趨勢性檢驗。考慮到黃土丘陵溝壑區降雨過程一般歷時較短,不超過12 h,因此最大12 h降雨能夠代表相應洪水的致洪暴雨,故在此處僅展示最大12 h降雨變化情況(圖2)。同時將與佳蘆河流域較近的榆林氣象站最大日降雨序列作為參考,一并進行檢驗。檢驗結果(表2)顯示,佳蘆河流域致洪降雨序列未發生顯著變化(包括線性和非線性一階矩、二階矩)。因此排除了降雨變化造成洪峰流量非一致性變化的可能。 圖2 申家灣站年最大洪峰流量序列與致洪暴雨序列 表1 佳蘆河流域洪峰流量序列及其影響因子的趨勢性分析 表2 佳蘆河流域致洪降雨序列趨勢性分析 3.2 溯源重構序列的生成通過對流域實測資料的分析,我們可以得到這樣的認識:佳蘆河流域的降雨未發生顯著的非一致性變化,申家灣站年最大洪峰流量序列的非一致性變化主要產生于流域有效產流面積和植被覆蓋度的顯著變化。因此,根據溯源重構法的思想,重構時不考慮降雨因子,僅考慮有效產流面積與植被覆蓋度兩個因子。在對洪峰流量序列進行重構之前,首先要分析出有效產流面積和植被覆蓋度對洪峰流量作用的源函數。 3.2.1 源函數的建立方法 源函數是溯源重構法的關鍵,也是提升對水文過程認知的重要基礎,是不應該被忽略的學術問題。它的確定應該來自于理論推導或實驗,但現階段,介于水文過程的復雜性,基于理論和實驗手段成功確定出的源函數幾乎看不到。因此,本著影響因子的作用規律必然體現在統計規律中的認識,我們可以通過回歸的方法來逐個估計源函數的近似值。為敘述方便,這里令Y表示洪峰流量,X1和X2分別表示流域有效產流面積和植被覆蓋度。源函數建立的具體做法:首先建立第一個因子X1與Y的關系f1(X1(t)),并作為X1的源函數作用于Y,之后將該因子的影響從Y序列中排除,即,再建立剩余序列與第二個因子X2的源函數f2(X2(t))。推廣而言,若選擇了m個有趨勢變化的影響因子,則第3個影響因子的源函數由與第3個因子的關系估計,依次進行,直到m個因子的源函數被估計出。 顯然,這種做法會帶來因影響因子的引入順序改變各因子源函數形式的問題。理論上,真實的源函數將不會受重構順序的干擾。而實際中,由于源函數是估計函數,重構順序的干擾是可能存在的,為避免這個問題,可根據各影響因子與研究變量之間相關性的強弱順序確定重構順序。 3.2.2 有效產流面積與植被覆蓋度的單因子源函數 所謂單因子指只有一個非一致性性影響因子。眾多的研究成果證明洪峰流量和流域面積之間呈現冪函數關系[31-32]。權琦澤[33]的研究結果表明榆林地區洪峰流量與流域面積的0.73次方成正比,故假定有效產流面積的源函數的估計為 植被對洪峰流量的作用關系研究不多見。根據周宏飛等[34]在徑流試驗場的實驗研究成果,徑流深與植被覆蓋度FVC間呈現指數函數關系: 式中:R為徑流深,mm;k為經驗參數。借助洪峰與洪量間的冪函數關系、洪量與徑流深間的關系,便可由式(15)得到洪峰流量與植被覆蓋度間的作用規律:Qm∝eαFVC,因此植被覆蓋度FVC對洪峰流量作用的源函數估計式為式(16): 通過實測洪峰流量和eαFVC之間的回歸,得佳蘆河流域的參數α為-0.071,即: 3.2.3 年最大洪峰流量的溯源重構序列 當確立了有效產流面積和植被覆蓋度這兩個變化因子的源函數后,根據式(13)定義的溯源重構函數,建立佳蘆河流域的溯源重構函數。為了比較溯源重構方法的有效性,分別建立單個因子和兩因子的溯源重構函數如下: 利用有效產流面積的單因子重構: 利用植被覆蓋度的單因子重構: 利用有效產流面積和植被覆蓋度兩因子重構(方法見3.2.1節): 其中fFVC(FVC)=eαFVC中的α=-0.059則由RSA,t與eαFVC的回歸得到。 理論上講,若源函數是通過理論分析與實驗分析的方式確定,則無論是單因子重構還是兩因子重構,源函數不應發生變化。這里α 取值的差異正是源函數的估計受到重構順序影響的體現。因此,實際應用中建議根據各影響因子與研究變量之間相關性的強弱順序確定重構順序。將洪峰流量序列Qm,t及其影響因子序列Ae,t和FVCt的值分別代入式(18)—(20)中,得到相應的溯源重構序列RSA,t、RSFVC,t和RSdouble,t。 按照本文提及的溯源重構理論建立的溯源重構方法,其實質是一種轉換方法,所獲得的重構序列RSt理應是一個具有一致性的隨機序列。作為驗證,本文以第3節中的溯源重構序列RSA,t、RSFVC,t和RSdouble,t為對象,通過考察其趨勢性變化,探究溯源重構理論的正確性和溯源重構序列的合理性。同時,鑒于以下兩個原因,對重構序列的特征進行探討同樣顯得必要。①雖然RSt(如RSA,t、RSFVC,t和RSdouble,t)不是直接觀測變量,但因它是由觀測變量計算出來,因此有物理意義:相當于模數,應該具有它的特征;②實踐中,在溯源重構時,隨趨勢性影響因子識別的完整性不同,所獲得的重構序列會具有不同的特征。因此重構序列的特征分析對于溯源重構序列RSt的應用起著理論支撐作用。 4.1 溯源重構序列的趨勢特征采用同樣的假設檢驗方法,對上述溯源重構序列的趨勢性加以檢驗,檢驗結果見表3。可以看出,具有顯著趨勢性變化的原洪峰流量序列經單因子溯源重構后,重構序列的各種相關系數均比原序列相應相關系數減小,說明不論是線性趨勢還是非線性趨勢均得到一定的消除;特別是雙因子重構后,Pearson相關系數和Spearman秩相關系數均小于相應的臨界值,說明溯源重構序列RSdouble,t已無顯著趨勢存在,且Breusch-Pagan 檢驗統計量c也由25.406 減小到5.157,盡管仍大于臨界值,但洪峰流量序列二階矩的非平穩性得到很大改善,說明引入非平穩變化的影響因子越合理,重構序列的平穩性越好。不僅如此,原序列存在的突變也得到消除,見圖5。 圖5 溯源重構序列與年最大洪峰流量序列的對比 表3 年最大洪峰流量溯源重構序列一致性檢驗 檢驗結果表明,溯源重構方法在消除非一致性序列的非一致性(包括線性、非線性趨勢和突變)方面具有統計意義上的有效性。 4.2 溯源重構序列的分布特征分布特征是隨機變量取值特性的完整描述,是研究隨機現象的核心。這里討論年最大洪峰流量溯源重構序列的分布函數,并與基于時變矩獲得的洪峰流量序列(原序列)的分布函數進行比較。同時,針對當前工程師們無奈之選,即無視非平穩的存在,直接進行傳統頻率分析得出的分布函數也一并列入比較。 針對3.2 節得到的佳蘆河年最大洪峰流量的溯源重構序列RSdouble,t,本文選取水文領域常用的Weibull(WEI),Log-normal(LN),Gamma(GA),Gumbel(GU)和GEV 五種分布類型作為備選分布,利用線性矩法[35]估計分布參數,依據納什效率系數[36-37]、均方根誤差RMSE等擬合優度準則確定最優分布。申家灣站溯源重構序列的最優分布為GEV,對應的分布參數分別為μ=9.657,σ=83.525,κ=0.878。對于非一致性序列的時變分布則基于GAMLSS模型[38]采用時變矩法確定,備選分布仍選取上述五種類型,以有效產流面積與植被覆蓋度作為協變量,評價準則為AIC準則[39],具體見表4。而無視非一致性存在,直接以非一致性原洪峰流量序列估計的總體分布也列于表4。 表4 不同方法確定的年最大洪峰流量序列的分布類型 理論上,年最大洪峰流量序列屬于極值序列,它的分布應該是極值型。從表4可以看到不同屬性序列和不同分析方法所挑選出的分布函數不同,其中只有溯源重構序列的分布符合極值型,本文作者對陜西省榆林地區大理河等6個流域的年最大洪峰流量溯源重構序列進行分布函數分析,結果均為極值類分布,這說明溯源重構法可以體現原序列的極值屬性。這種既平穩又符合抽樣特點的序列表明溯源重構法的理論正確,所得序列可用。對于非一致性原序列,相較于傳統方法,時變矩法因考慮了原序列非一致性的特征,所以挑選出了與極值類型相接近的GA分布。有趣的是若直接應用非一致性原序列,采用傳統方法分析出的分布函數卻是不同于極值型分布的LN分布。這一結果從側面反映了水文序列分布的確定會受到參數估計方法的影響,即估計方法越適應序列屬性,所選擇出的分布越可靠。 利用頻率分析推求水文設計值是水資源利用、管理與保護領域的最基本問題。合理的設計值理應由合理的分布確定。Li等[22]在研究淤地壩影響下的設計洪水計算問題時,所采用的去非平穩性方法實質上正是溯源重構思想的體現。其獲得的合理結果同樣證明溯源重構方法獲得的概率分布合理,同時說明該方法在非一致性序列頻率分析方面具有良好的適應性。 4.3 與其他構建一致性序列方法比較溯源重構法的思想是通過溯源重構將非一致性序列轉變為一致性序列,為以一致性序列作為基礎的分析計算工作提供樣本資料。這種想法同樣體現在還原或還現法和分解合成法中。但由于方法所依據的原理不同,方法的應用效果隨之不同。 還原或還現法依據的原理是通過對水文變量系統性變化的增量回加到原序列或對水文變量進行修正,達到使水文變量序列一致的目的。在增量的量化或修正值的量化工作中,由于要求資料的種類多、數量大,且對資料的準確性依賴程度高,使用不易。同時牽扯的一些概念難以精確界定[40],存在方法失真或失效[41]等問題。即便用分布式水文模型直接計算增量,也會面臨資料的非一致性導致模型參數率定(優化法)的不確定性加大問題[41]。正因如此,本文不做具體的分析對比。 分解合成法[42]認為,“無論水文現象的變化多么復雜,水文序列總可以分解成確定性成分和隨機性成分這兩部分。一般來說,水文序列的確定性成分主要受人類活動的影響,但并不排除氣候因素(如氣候轉型期)和下墊面因素(如火山爆發、地震等)的影響,其變化規律可以在較短的工程年代里發生緩慢的漸變或劇烈的突變,因此水文序列中確定性成分的變化規律往往是非一致的。而水文序列的隨機性成分則主要受氣候、地質等因素的影響,其變化規律需要一個漫長的地質年代才能改變,因此水文序列中隨機性成分的統計規律是相對一致的。”于是謝平等[42]建議采用成因分析法與統計分析法分別對確定性成分和隨機性成分進行識別與檢驗,并對確定性成分進行擬合計算,對隨機性成分采用傳統方法進行頻率分析計算。后者意味著分解合成法獲得的隨機變量樣本是一個簡單隨機樣本。下面將繼續以佳蘆河流域年最大洪峰流量序列資料,研究分析分解合成法生成的隨機樣本特征。 根據分解合成法原理,非一致性水文序列Xt可按下式表示: 式中:Yt為確定的非周期成分(包括趨勢、跳躍等);Pt為確定性的周期成分(包括簡單的或復合周期的成分等);St為隨機成分。 為避免周期對趨勢的影響,這里首先進行周期分析,利用小波分析[43]得到周期序列存在21年、9年兩個顯著周期,由此獲得周期函數如式(22): 剔除周期后發現序列仍存在明顯的趨勢,通過回歸分析得到式(23)所示的趨勢成分: 根據式(21)剔除周期成分與趨勢成分后得到隨機序列St,見圖6,對該隨機序列進行趨勢檢驗,結果見表5。 圖6 分解合成法構建的佳蘆河年最大洪峰流量一致性序列 表5 分解合成法構建的佳蘆河年最大洪峰流量序列的一致性檢驗 分解合成法獲得的佳蘆河年最大洪峰流量的重構序列十分有效地消除了一階矩的顯著線性趨勢,但Spearman秩相關系數依然大于臨界值,表明其一階矩的非線性型非一致性仍然顯著存在;方差的非一致性檢驗統計量χ為23.064,幾乎沒有任何改善,說明分解合成法重構的隨機成分并非簡單樣本。 產生上述現象的原因可以概化為兩個方面。一是由于定義兩種成分的物理機制均不夠清晰,例如分解合成法原理述及的“水文序列的確定性成分主要受人類活動的影響,但并不排除氣候因素(如氣候轉型期)和下墊面因素(如火山爆發、地震等)的影響”與“隨機性成分則主要受氣候、地質等因素的影響,其變化規律需要一個漫長的地質年代才能改變”,其中氣候轉型期以及需要漫長的地質年代才能改變的氣候因素無法清晰界定,更不能明確表達,因此確定性成分的擬合具有較大的不確定性,由實測資料推求出的隨機性成分為實測資料與確定性成分之差,就會具有較大的不確定性;二是該方法假定水文序列Xt的各個成分滿足線性疊加特性(即疊加模型)[44]。因此,根據上文疊加模型與乘積模型的對比分析,分解合成法構建的“相對一致”性序列僅能實現均值一致,而方差非一致的現象就不難理解了。這也成為了疊加模型無法描述序列的二階矩變化的例證。 相比之下,溯源重構法認為水文變量Y的變化是一系列影響因子自身的非一致性變化引起的。這些因子的非一致性影響通過它們各自的源函數作用于Y。如果將全部非一致性變化因子的作用從Y序列中剔除,則剔除后的序列RSt就是一致性序列。與分解合成法不同,溯源重構法中的隨機成分是指未被人類認知的次要因子的作用,無需專門率定。同時溯源重構法的基礎模型采用乘法模式,更符合水文系統的非線性相依特征。溯源重構法的物理含義明確,分析的不確定性相對較小。 眾所周知,任何現象都有其因果關系,以數學術語來說,即因變量與自變量的關系。作者認為,水文變量Y的非一致性變化是由于自變量(影響因子)自身的非一致性變化所引起的。據此提出溯源重構法,即從源函數概念出發,依據因變量與自變量間的物理機理所建立起的統計模型,從因變量Y序列中剔除非一致性變化的自變量影響,實現非一致性序列Yt向新的一致性序列RSt的轉化,從而可以服務于以一致性序列為基礎的分析計算工作。溯源重構法在統計原理的基礎上充分考慮了水文現象的物理成因,在原理上不同于分解合成法和還原或還現法。溯源重構法采用源函數描述影響因子Xi作用于Y的規律。源函數是一種機理函數,具有時不變的特性。同時溯源重構法的基礎模型采用乘積模型,更符合水文系統的非線性相依特征。該方法物理含義明確,分析的不確定性相對較小。 依據佳蘆河流域申家灣水文站的實測資料,應用溯源重構法實現了非一致性年最大洪峰流量序列向一致性的溯源重構序列的轉化,結果表明溯源重構法能夠有效消除年最大洪峰流量序列存在的突變及一階矩的線性或非線性趨勢,也能夠消除二階矩的非一致性。與分解合成法相比,該方法的目標也是試圖獲得一致性序列,但分解合成法僅能去除序列一階矩的線性趨勢,無法去除序列非線性趨勢以及方差的非一致性。相比于時變矩法確定出的時變概率分布,以及直接應用非一致性原序列強行估計出的總體分布,溯源重構序列的分布函數更符合原序列極值抽樣的統計屬性。因此,溯源重構法所構成的序列類似于原序列的模數序列,除可以用于水文頻率分析外,還可以通過對溯源重構序列構建預測模型,實現溯源重構法在水文預測預報領域的應用,并獲得不確定性相對較小的預報成果。事實上,只要科學合理的表達影響因子X,例如本文第3節中,若佳蘆河流域內淤地壩發生漫壩或潰壩情形時,只需要對X,即有效產流面積,進行合理修正,就可以繼續沿用重構函數獲得性質相同的序列,因此溯源重構法具有實際應用前景。
3 實例研究











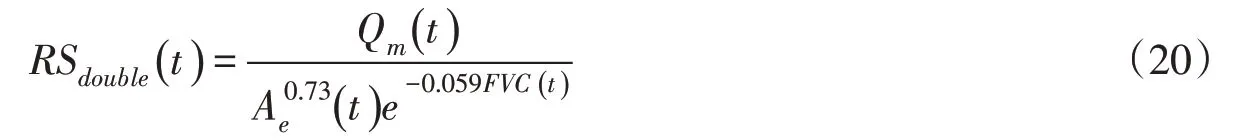
4 討論




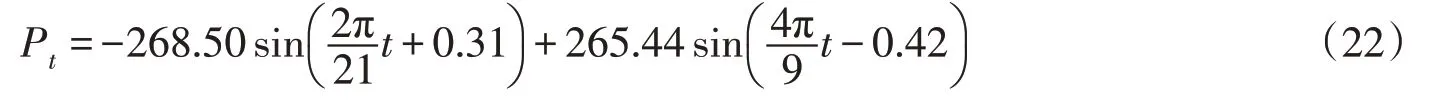



5 結論

