迭代法解析核信號成形電路數(shù)字解

李樂賽 周建斌 洪 旭 馬英杰 劉 易

（成都理工大學核技術(shù)與自動化工程學院 成都610059）

常見核領(lǐng)域電路的公式推導大都采用拉普拉氏變換［1］，缺點是既不夠普遍，不適用于所有的電路，且推導過程復雜。本文采用數(shù)值解的方法來推導核領(lǐng)域中常見的C-R、R-C、S-K濾波電路，但并未采用遞歸的方法，遞推法需設(shè)定恰當?shù)妮敵鲭妷撼踔担拍艿玫嚼硐氲倪f歸值［2-7］。實測條件下初值未知，不恰當?shù)某踔翟O(shè)定可能導致錯誤。而迭代法初值為假設(shè)值，對結(jié)果無影響。本文采用數(shù)值解中的迭代法推導電路的輸出信號，得到的輸出電壓值精度可調(diào)［8-9］。迭代法與遞歸法得到的結(jié)果基本一致，誤差精度上高于10-11，且迭代解與解析解的誤差由數(shù)據(jù)采樣率決定，故通過提高數(shù)據(jù)采樣率能降低差值，誤差可控［2］。

1 Jacobi迭代法

Jacobi迭代法的計算過程中系數(shù)矩陣A始終不變，容易并行計算。對于線性方程組：

式中：A為非奇異矩陣；x為解向量；b為常數(shù)向量。

解Ax=b的Jacobi迭代法的分量形式為［8］：

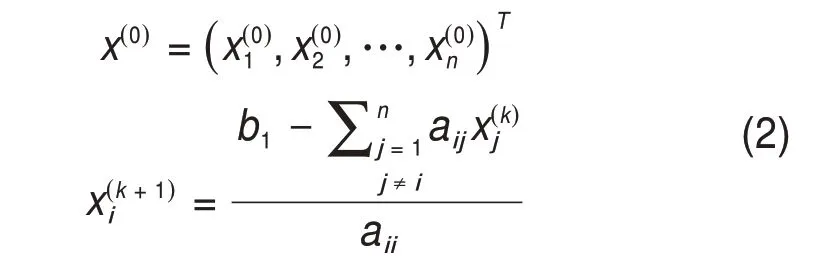
i=1，2，…，n；k=0，1，…迭代次數(shù)

2 R-C、C-R成形模型迭代法

2.1 R-C積分電路

R-C積分電路是核電子學電路中常用的濾波電路，圖1（a）為R-C積分電路，輸入信號為Vin、輸出信號為Vout。基于基爾霍夫電流定律（Kirchhoff's Current Law，KCL）該電路可以等效成式（3）。

電容屬于抗性器件，涉及到瞬態(tài)分析，可通過隱式歐拉法將微分化為差分。令極短時間Δt，則：

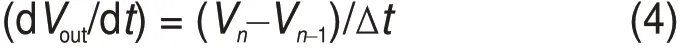
Vn和Vn-1分別代表nΔt和（n-1）Δt時刻電容兩端電壓值，式（4）化成：

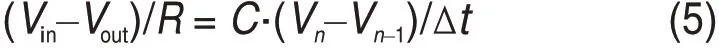
式（5）可化為：

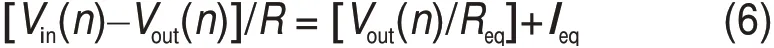
式中：Req=Δt/C，Ieq=C·(Vn-1)/Δt，即將電容看作一個電阻并聯(lián)上電流源，等效模型如圖1（b）所示［10］。

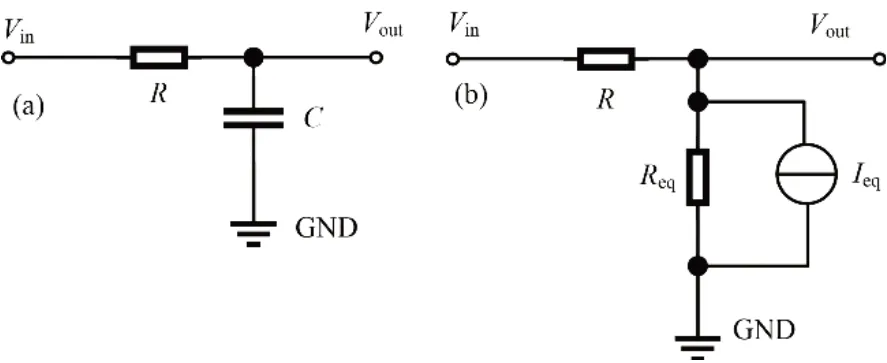
圖1 R-C積分電路(a)與等效電路(b)Fig.1 R-C integral circuit(a)and its equivalent circuit(b)

整理得：

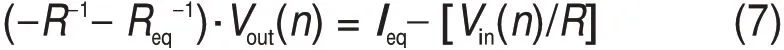
已知采樣步長時間Δt，假設(shè)初始電壓Vout（0），設(shè)置迭代精度e，通過某時刻輸入信號Vin（n）能迭代出滿足精度要求的輸出電壓Vout（n）。……