改進的窗參數優化S變換及其在河道檢測中的應用

張付璦 陳學華* 羅 鑫 張 杰 徐 赫

(①成都理工大學油氣藏地質及開發工程國家重點實驗室，四川成都 610059；②成都理工大學地球勘探與信息技術教育部重點實驗室，四川成都 610059)

0 引言

時頻分析方法[1]是一種時變非平穩信號處理方法，它對信號進行時頻分析處理，得到時頻域信號的能量分布，是地震資料精細構造解釋和儲層預測的有力工具。

基于傅里葉變換的時頻分析方法發展很快，如：Gabor[1]提出的短時傅里葉變換；Morlet等[2]提出的小波變換；Stockwell等[3]結合前兩種方法的優點提出的S變換。但上述方法受到自身固有的測不準原則所限，時頻分辨率無法達到很好的效果，為了達到最佳效果，研究人員又提出了各種改進的時頻分析方法。陳學華等[4]提出廣義S變換，引入了λ和p兩個參數共同控制窗函數，相比S變換具有更好的適應性和更高的時頻分辨率；Lu等[5]基于零相位自適應魯棒濾波器提出了一種加窗Hilbert變換；Gholami等[6-7]利用混合范數稀疏性，提出稀疏短時傅里葉變換；Sattari等[8-9]考慮到地震數據頻率的迅速變化，提出了一種新的基于快速稀疏的S變換。這些改進的方法使時頻分辨率得到較大的提升，并且廣泛應用于地震資料低頻陰影分析、斷層識別、彈性參數反演和河道檢測等[10-12]。在實際應用中取得的效果證明了時頻分析方法的有效性。高靜懷等[13]將廣義S變換應用于薄互層模型分析；陳學華等[14]利用高階偽希爾伯特變換對河道、斷層等不連續信息進行預測；對于依賴頻率的AVO反演，時頻分析方法則直接影響反演結果的分辨率[15-16]。此外，在流體流度屬性的提取中，高精度時頻分析方法也有廣泛應用[17-21]。

隨著地震勘探技術不斷發展，地震資料解釋的精度要求越來越高，需要利用更加有效的時頻分析方法從地震數據中提取有效信息。因此，進一步改進和發展高分辨時頻分析方法仍是開展地震資料精細儲層描述的關鍵環節。本文在窗函數優化S變換[9]的基礎上，提出通過引入新的窗函數調節參數，構建改進的窗參數優化S變換方法，能夠根據實際信號的振幅譜自適應地求取最優窗參數，得到的時頻譜具有更高的時頻聚焦性和分辨率。通過合成信號對比分析，驗證了該方法在低、高頻端均具有較高分辨率；在實際地震資料的河道檢測中能更好地刻畫河道的空間展布特征，顯示的地質細節特征更清晰，利于地震資料的精細解釋。

1 方法原理

Stockwell等[3]首次提出了時頻分辨率隨頻率變化的時頻表示方法——S變換。它所選取的窗函數隨頻率的增加而自適應地調節時窗寬度。在S變換中，高斯窗函數的表達式為

(1)

式中：t為時間；σ為窗函數的調節尺度參數。

為了使窗函數隨頻率變化，定義σ為隨頻率f變化的函數，即

(2)

S變換的窗函數會根據頻率的增加而減小時寬，但在時域壓縮的同時會在頻域拉伸，存在時間分辨率和頻率分辨率不相容的問題。Sattari等[9]在S變換的基礎上，提出窗參數優化S變換，將傳統S變換中僅隨時間或頻率變化產生最優窗的問題轉化為一個二維的問題。通過優化的窗函數定位局部的強振幅頻率分量，并對弱振幅頻率分量進行模糊處理，從而控制二者在時頻譜上的影響區域。由于振幅譜中包含了頻率和振幅的信息，因此將其作為優化窗函數的參照。基于上述思想，本文設計了根據實際地震信號的振幅譜自適應確定最優窗參數的流程，并基于求取的最優化窗參數構建了改進的窗參數優化S變換方法。優化流程如下。

(1)對原始信號x(t)求取振幅譜

X(f)=abs{FT[x(t)]}

(3)

式中FT表示傅里葉變換。

(2)對振幅譜X(f)進行平滑處理

Xs(f)=smooth[X(f)]

(4)

(3)保證平滑后的結果均大于0，即

(5)

(4)歸一化

(6)

(7)

式中r為可調節參數。通常對于帶限信號，r取1或2；對于地震信號，r取3或4；對于帶寬信號，r取5～10。

(6)求得隨頻率變化的最優窗參數

(8)

式中N表示離散信號點的個數。

通過r優化后的窗參數優化S變換，使信號時頻聚焦性和分辨率有了一定的提高，但仍有改進的空間。之后引入λ、p(λ>0,0.5≤p≤1.5)兩個參數，共同調節窗參數s(f)。在實際應用中，根據實際信號的特征靈活選擇λ、p，當λ取值過大時，可適當調整p值，從而得到最佳的窗參數。

λ、p兩個參數的進一步優化，使改進后的調節參數可以根據實際應用中非平穩信號的頻率分布特點和時頻分析的側重點，調節窗函數隨頻率變化的速度，能夠靈活地適應具體信號。

進一步構建出改進的窗參數優化S變換的調節參數為

(9)

由此得到改進的窗函數

(10)

得到改進的窗參數優化S變換表達式

(11)

式中τ為窗函數中心點，控制窗函數在時間t上的移動。

圖1顯示不同處理流程對窗參數的優化效果。圖1a為合成信號時域波形，對合成信號分別做S變換、窗參數優化S變換和改進的窗參數優化S變換，并與信號的振幅譜(圖1b)進行對比。由圖可以看出，窗參數的變化具有對稱性，其中S變換的窗參數呈線性變化(圖1c)，進行優化后的窗參數隨信號振幅譜自適應變化(圖1d)，本文方法對優化的窗參數又有進一步改進，得到的窗參數能夠更好地適應信號的突變(圖1e)。

圖1 信號振幅與不同處理方法窗寬的關系

優化后的窗函數可以根據實際信號的振幅區分不同的頻率分量，同時在時間和頻率域也具有自適應性。λ和p兩個可調節參數的引入，使變換處理更具靈活性，時頻聚集性更好，對非平穩信號中的各種分量區分能力更強，因而該方法得到的時頻譜具有較高的時頻分辨率。此外，當λ=1、p=1時，該方法即等價于窗參數優化S變換。

2 模型試算與分析

為了便于分析本文方法的效果，設計了一個合成的非平穩信號進行模型試算。信號由兩個不同頻率成分的Chrip信號組成(圖2a)。對該信號分別做S變換、窗參數優化S變換(r=10)和改進的窗參數優化S變換(r=10，λ=6，p=0.5)，分別得到對應的時頻譜(圖2b～圖2d)。對比可知，窗參數優化S變換(圖2c)相比S變換(圖2b)具有更高的頻率分辨率，尤其在高頻部分優勢更加明顯，原因在于窗參數優化S變換在S變換的基礎上對強振幅頻率分量進行了適應性調節，因此得到的時頻譜分辨率更高，聚焦性更好。而相比窗參數優化S變換的結果，改進的窗參數優化S變換(圖2d)不僅在高頻端保持了很高的分辨率，在低頻端分辨率也有明顯的提升，能夠更清楚地分離兩個不同頻率分量的信號，說明本文方法具有更強的信號區分能力。

圖2 合成的Chrip非平穩信號及不同方法處理的時頻譜

3 實際地震資料處理

將本文方法應用到某海上工區的實際地震資料處理。圖3a為工區內提取的原始地震剖面(圖中藍色線為解釋的目的層)，對地震數據分別做S變換、窗參數優化S變換(r=3)和改進的窗參數優化S變換(r=3，λ=8，p=0.5)后，抽取40Hz的共頻率剖面進行對比分析。由圖3可見，改進的窗參數優化S變換得到的共頻率剖面(圖3d)分辨率更高，并且具有很好的橫向連續性，可以更好地表現地震記錄隨時間的變化。說明本文方法在提升時頻聚焦性和時頻分辨率方面效果更佳，能更好地適應非平穩信號的突變。

圖3 原始地震剖面及不同方法處理后的40Hz共頻剖面

從圖3所示剖面中抽取第500道地震記錄進行單道時頻分析，結果顯示，本文方法S變換結果同樣顯示出更好的時頻聚焦性和更高的分辨率，頻譜能夠更加清晰地反映地震記錄的變化(圖4d中紅色虛線框標識處)，說明改進的窗參數優化S變換在實際應用中更具優勢。

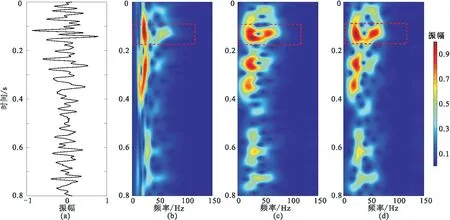
圖4 單道地震記錄及其不同方法處理的時頻譜

為進一步說明本文方法的實用性和優越性，將上述三種S變換方法應用于整個工區三維地震數據體處理。圖5為原始地震數據體中抽取的沿層切片(圖中黑線為圖3選取的剖面位置)。由圖可見，該地區河道較為發育，但是切片上顯示的河道特征比較模糊，難以獲得有效的細節信息。分別采用不同方法對三維數據進行瞬時譜分解，然后從不同方法處理得到的40Hz數據體中抽取沿層切片，進行河道特征分析。結果顯示，在常規S變換(圖6a)和窗參數優化S變換(圖6b)結果中,能夠顯示出較大尺度的河道(圖中黃色矩形虛線框所示)，但是背景比較模糊；在本文方法處理的結果中，除了清晰顯示較大尺度的河道外，還能見到一些更小細節的河道(圖6c中紅色橢圓虛線框所示)。此外，從圖6c中還觀察到一些隱蔽的河道(圖中橙色箭頭所示)，而該特征未在圖6a和圖6b中清晰顯示。說明改進的窗參數優化S變換結果能夠更加清晰地顯示河道的形態和分布，刻畫更多的細節特征。圖6d為應用本文方法對數據體進行分頻處理后，對40、60、80Hz的單頻振幅譜進行RGB融合[22-24]得到的切片。圖中同樣顯示出了隱蔽河道的位置和細節，且更為清晰。

圖5 原始地震數據沿目的層的振幅切片

圖6 不同方法處理數據體抽取的沿層切片

4 結論

本文基于窗參數優化S變換，通過引入新的調節參數，構建了一種改進的窗參數優化S變換方法，合成信號和實際資料的應用結果均表明該方法具有時頻分辨率高和能量聚集性好的優勢。在三維地震資料的河道檢測中，改進的窗參數優化S變換的處理結果效果更好，能夠更清晰地刻畫出河道的形態，顯示河道的連續性，為地震資料精細儲層描述提供了有力的技術支持。此外，該方法在地震屬性分析、彈性參數反演等方面也具有良好的應用前景。