離心壓縮機葉輪材料屬性失諧對其振動局部化的影響研究

成 科，常 超

（1.中國石油化工股份有限公司 洛陽分公司，河南洛陽 471012；2.合肥通用機械研究院有限公司 壓縮機技術(shù)國家重點實驗室，合肥 230031）

0 引言

大型離心式壓縮機在工程中的應(yīng)用越來越廣泛。隨著葉輪結(jié)構(gòu)尺寸的持續(xù)增大，葉輪整體剛性的減弱是必然出現(xiàn)的結(jié)果。除此之外，因為存在加工工藝非均勻性偏差、機組運行過程中介質(zhì)對旋轉(zhuǎn)部件存在摩擦沖刷作用、工質(zhì)在葉片上聚集和附著等因素，導(dǎo)致在某些葉片上結(jié)構(gòu)和屬性有著不同于其它葉片的微小差別。這種差別對葉輪的循環(huán)對稱結(jié)構(gòu)造成破壞，形成了葉輪的失諧。

近年來，許多學(xué)者在葉輪機械振動模態(tài)局部化影響機理方面做了大量的CFD模擬及試驗研究。JUDGE等［1］開展了一系列試驗研究，主要針對隨機失諧狀態(tài)下的葉片影響葉輪整體結(jié)構(gòu)模態(tài)局部化的機理、表現(xiàn)以及葉輪受迫響應(yīng)的機理，其有關(guān)模態(tài)局部化的發(fā)生、受迫響應(yīng)幅值的提高以及因失諧而導(dǎo)致的共振頻率如何發(fā)生改變等問題的理論分析得到了試驗證明。XIE等［2］對失諧的葉片-輪盤結(jié)構(gòu)的振動局部化問題進行了研究，采用模態(tài)綜合法，提出了計算模態(tài)局部化因子的方法。賀爾銘等［3］通過簡化系統(tǒng)，采用質(zhì)量-彈簧組合系統(tǒng)的模型和方法，對阻尼、激振力、失諧強度、耦合強度的階次和葉片數(shù)等參數(shù)對于系統(tǒng)受迫振動特性的影響規(guī)律進行了研究，得到的結(jié)論對后續(xù)研究具有非常重要的指導(dǎo)意義。王紅建等［4］重點分析了非線性的干摩擦力作用下散亂失諧葉片-輪盤系統(tǒng)受迫響應(yīng)的規(guī)律，采用的是諧波平衡法和快速傅立葉變換技術(shù)。戴靜君等［5］在理論分析和試驗研究中，將模型進行結(jié)構(gòu)簡化，使葉片結(jié)構(gòu)模擬為固定在輪盤上，主要分析了葉片失諧量及工作轉(zhuǎn)速對循環(huán)葉輪結(jié)構(gòu)振動模態(tài)局部化產(chǎn)生的影響和規(guī)律。

筆者在研究中發(fā)現(xiàn)，材料物理特性諸如楊氏模量、密度、泊松比等參數(shù)的失諧，同樣會導(dǎo)致葉輪的失諧，使葉輪局部或較大范圍內(nèi)產(chǎn)生疲勞失效，不利于旋轉(zhuǎn)設(shè)備的長周期穩(wěn)定運行，因此，對其相關(guān)機理和內(nèi)在規(guī)律的研究是必要和有意義的。

1 振動模態(tài)局部化理論和有限元方法

振動局部化問題在結(jié)構(gòu)動力學(xué)中主要反映在模態(tài)的局部化和振動傳遞的局部化2個方面。模態(tài)局部化分為模態(tài)振型局部化和模態(tài)頻率轉(zhuǎn)向2種物理現(xiàn)象。模態(tài)振型的局部化指所研究系統(tǒng)的模態(tài)振型并沒有“擴展”到整個結(jié)構(gòu)，而只集中在局部的子結(jié)構(gòu)上。對于本文的研究對象離心壓縮機葉輪，振動局部化就是一個或幾個扇區(qū)子結(jié)構(gòu)產(chǎn)生明顯大于其它子結(jié)構(gòu)的振動，導(dǎo)致這一部分的葉片振動響應(yīng)過于激烈，同時會產(chǎn)生較大的應(yīng)力，進而可能引發(fā)疲勞斷裂等嚴(yán)重后果。

本文采用有限元方法以葉輪材料的楊氏模量為參考值，根據(jù)葉輪網(wǎng)格劃分后的單元總數(shù)，使用特定的概率分布函數(shù)生成楊氏模量的隨機序列，將其逐一分配至各個單元，獲得給定概率統(tǒng)計分布規(guī)律下的楊氏模量失諧分布，并對其進行分析。

2 葉輪材料屬性失諧模型的建立

2.1 三維模型的導(dǎo)入及網(wǎng)格劃分

離心壓縮機的葉輪型式多樣，根據(jù)不同的使用工況和性能參數(shù)［6-8］，在尺寸、葉型和結(jié)構(gòu)上都存在差異。考慮到本文研究的內(nèi)容，選取的研究對象是已投入實際工業(yè)系統(tǒng)工作的一臺閉式三元葉輪。基本參數(shù)見表1。

表1 葉輪基本參數(shù)Tab.1 Basic parameters of impeller

離心壓縮機葉輪三維模型如圖1（a）所示。采用非結(jié)構(gòu)化的網(wǎng)格單元對葉輪模型進行網(wǎng)格劃分。采用Brick 20 node 186單元，其屬于高階三維單元，具有20節(jié)點固體結(jié)構(gòu)。選取邊界長度為0.02 m的單元對模型進行網(wǎng)格劃分，結(jié)果如圖1（b）所示。

圖1 離心壓縮機葉輪三維模型及網(wǎng)格劃分Fig.1 3D model of centrifugal compressor impeller

2.2 葉輪材料屬性失諧的統(tǒng)計分布

為使計算簡化，現(xiàn)作如下假設(shè)：（1）葉輪材料屬性在總體上呈現(xiàn)出失諧分布，但是對于每個單元體，可以認為其內(nèi)部材料屬性是均勻的；（2）材料屬性的失諧會導(dǎo)致在局部出現(xiàn)各向異性，但在各單元內(nèi)部，仍認為其材料符合各向同性，并服從廣義胡克定律；（3）材料屬性即楊氏模量、泊松比和密度之間相互獨立。即認為楊氏模量的分布變化不影響泊松比和密度的分布，反之亦然。

由于本文主要探討葉輪整體失諧對其特性的影響，因此假定其材料屬性服從某種隨機統(tǒng)計分布。本文采用了比較符合實際情況的正態(tài)分布來描述材料屬性的失諧。

正態(tài)分布規(guī)律的概率密度函數(shù)為：

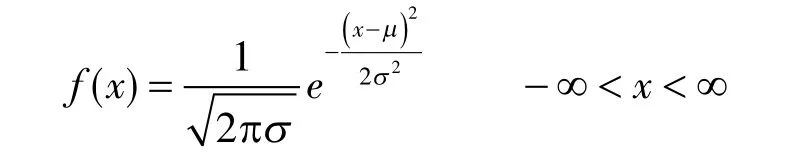
其中，μ與σ＞0是常數(shù)。

2.3 材料屬性隨機分布的生成及對單元體賦值

依據(jù)上文作出的假設(shè)，在失諧模型中，任意一個單元都按照均勻?qū)傩詠碓O(shè)置，而單元與單元之間則使用正態(tài)分布對材料屬性進行分配。由于研究對象形狀和尺寸的復(fù)雜性，在工程計算中，劃分出的單元體數(shù)量通常很龐大［9-22］。本文針對離心壓縮機葉輪的形狀特點，采用了循環(huán)賦值方法，具體操作如下：（1）先不考慮模型的材料屬性，直接使用文中提及的方法進行網(wǎng)格劃分；（2）使用APDL命令流語句生成符合正態(tài)分布的材料屬性值；（3）使用循環(huán)語句將上一步生成的材料屬性值賦值給每一個單元；（4）使用ANSYS中的PlotCtrls＞Style ＞Colors＞Reverse Video選項調(diào)整后，即可獲得葉輪模型，如圖2所示。

圖2 分配隨機失諧材料屬性后的葉輪模型Fig.2 Impeller model after assigning the randomly mistuned material attributes

如圖中色塊分布所示，不同的色塊代表不同的材料屬性。其中典型的楊氏模量數(shù)值對應(yīng)的單元體數(shù)目如圖3所示。可以看到，其分布基本符合正態(tài)規(guī)律，說明通過這種方式獲得的材料屬性失諧滿足本文要求。

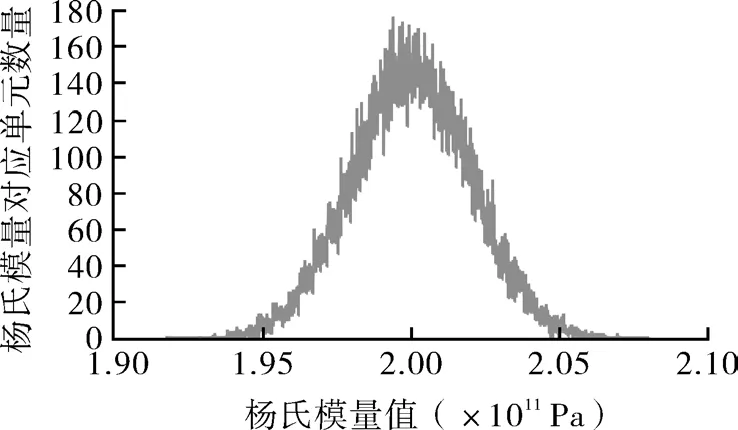
圖3 隨機生成楊氏模量數(shù)據(jù)分布統(tǒng)計Fig.3 Distribution statistics of the randomly generated Young’s modulus data

3 葉輪振動模態(tài)局部化問題分析

使用前述已完成建模及材料屬性分配的葉輪模型，分別對協(xié)調(diào)葉輪以及材料屬性失諧葉輪進行有預(yù)應(yīng)力的模態(tài)分析。計算中葉輪轉(zhuǎn)速為5 000 r/min。

3.1 協(xié)調(diào)葉輪的模態(tài)分析

首先考慮不存在任何材料屬性失諧的協(xié)調(diào)葉輪。因為本文研究的是高速轉(zhuǎn)動葉輪的模態(tài)，使用ANSYS中的MECHANICAL APDL對葉輪進行模態(tài)分析時，需要進行有預(yù)應(yīng)力的模態(tài)分析，即需要先進行轉(zhuǎn)動條件下的葉輪應(yīng)力分析。之后使用Block Lanczos法提取前40階固有頻率，將得到的協(xié)調(diào)葉輪固有頻率按模態(tài)階次進行排列，結(jié)果如圖4所示。

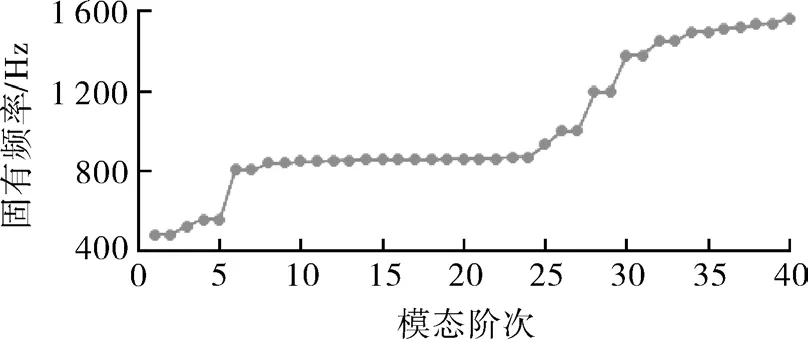
圖4 協(xié)調(diào)葉輪固有頻率Fig.4 The natural frequency of coordinated impeller

從圖可知，葉輪的固有頻率并不是按模態(tài)階次從低到高持續(xù)變化和上升的，而是以幾個階次為一組，固有頻率跳躍式上升，即所謂的重頻模態(tài)現(xiàn)象。

按照其分布規(guī)律，可將前40階固有頻率分為以下幾組：1～5，6～24，25，26～27，28～29，30～31，32～40。導(dǎo)出以上幾組數(shù)據(jù)中具有代表性的第3，8，25，34階云圖，如圖5所示。從圖可以看到，不同模態(tài)階次下的葉輪處于不同的振動型式。其中，從8～24階模態(tài)的位移云圖上可以清楚地看到，在葉輪上，相對于其他位置，葉片上位移的振動幅值更大，而輪盤和蓋盤上并沒有明顯振動。這說明在以后的分析和實踐過程中，如果只需要考慮葉片上的振動問題，那么就需要著重分析第17階模態(tài)。

圖5 各階模態(tài)位移云圖Fig.5 Modal displacement nephograms of each order

由于此時是使用協(xié)調(diào)葉輪進行模態(tài)分析，所以可以看到云圖上仍能呈現(xiàn)出一定的對稱形式。

3.2 失諧葉輪的模態(tài)分析

對葉輪整體的材料屬性分別設(shè)置以6%為間隔從3%～27%共5組數(shù)據(jù)的正態(tài)分布失諧量。對應(yīng)楊氏模量失諧、泊松比失諧以及密度失諧，共計15個失諧葉輪分別進行模態(tài)分析，將所得到的各組固有頻率同協(xié)調(diào)葉輪固有頻率進行比較、得出對應(yīng)階次的固有頻率的相對變化量，按階次重新排列后的模態(tài)特性分布如圖6所示。

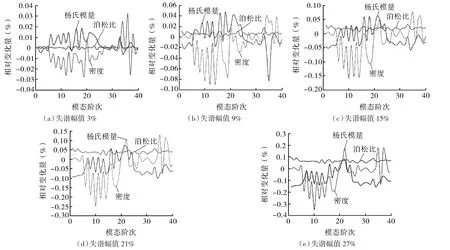
圖6 各組失諧葉輪固有頻率相對變化量Fig.6 Relative variation of natural frequency of mistuned impellers in each group

取出每一組失諧幅值中3種材料屬性在第1，3，4，6，8，25，26，28，30，32 和 34 階模態(tài)中對應(yīng)的固有頻率相對變化量，并進行重新排列，結(jié)果如圖7所示。

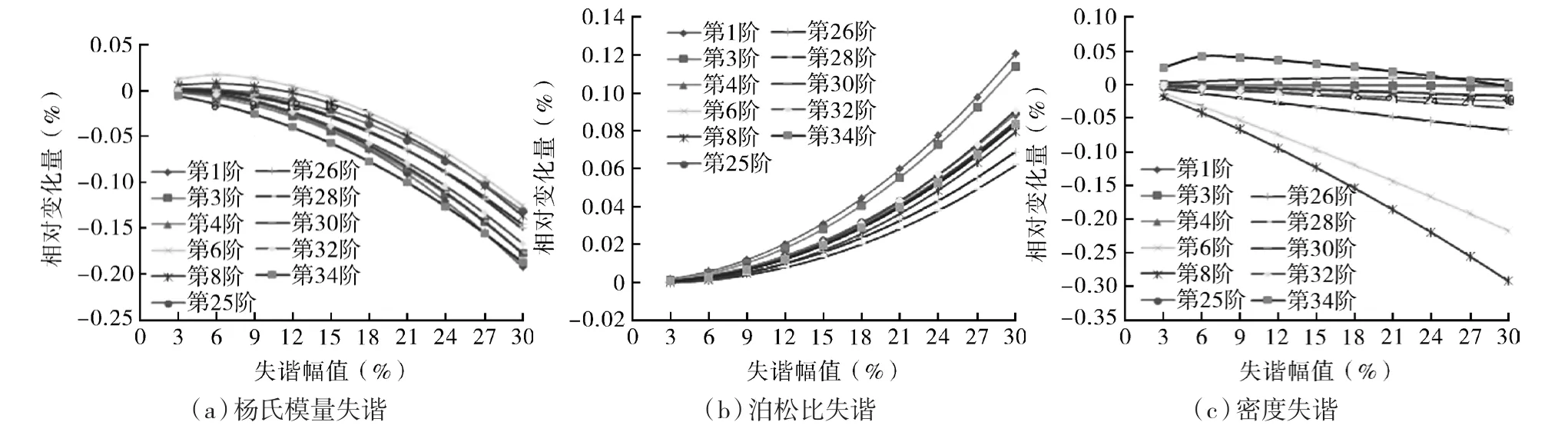
圖7 不同模態(tài)階次下固有頻率相對變化量隨失諧幅值的變化Fig.7 The change trend of relative variation of natural frequency with increasing mistuning amplitude for different mode orders

從圖7可知：

（1）總體上，密度失諧對葉輪固有頻率影響最大，楊氏模量次之，泊松比最小；

（2）泊松比失諧時，同一失諧幅值下，各階模態(tài)的固有頻率波動不是很大，總體的相對變化量隨著失諧幅值的增大而增大；

（3）楊氏模量失諧時，隨著失諧幅值的增加，葉輪固有頻率變化量先是逐漸增加，當(dāng)失諧到一定程度時，變化量又開始逐步減小；

（4）密度失諧時，從圖中可以觀察到，在第6階和第8階模態(tài)時，隨著失諧幅值的增加，固有頻率的變化和響應(yīng)非常明顯。第8階模態(tài)又屬于8～24階模態(tài)這一較寬范圍，這表明在這些模態(tài)范圍內(nèi)，密度的失諧對葉輪的振動特性可能產(chǎn)生更加明顯的影響。

當(dāng)材料屬性的失諧幅值控制在一定范圍內(nèi)時，可以根據(jù)上述計算得出的失諧葉輪固有頻率來選擇葉輪在實際運轉(zhuǎn)中的適當(dāng)?shù)墓ぷ黝l率，從而控制材料屬性失諧對振動模態(tài)的影響。

4 結(jié)論

（1）材料屬性失諧使得葉輪的固有頻率發(fā)生了變化。隨著失諧幅值的增大，楊氏模量失諧導(dǎo)致葉輪固有頻率相對變化量先增后減，泊松比失諧對應(yīng)的是固有頻率相對變化量逐漸增加。密度失諧則對葉輪一定范圍的固有頻率影響顯著。

（2）通過綜合考慮在一定失諧幅值范圍內(nèi)，3種材料屬性失諧對葉輪固有頻率的影響，就可以適當(dāng)選擇葉輪的工作頻率，避開葉輪的實際固有頻率，從而有效控制材料屬性失諧對葉輪振動模態(tài)的影響。