基于響應面法的柱塞泵迷宮密封優化設計

楊煜兵，張春光，劉光恒，李上青，張俊峰，安 磊，褚 帥

（沈陽儀表科學研究院有限公司 研究開發部，沈陽 110043）

0 引言

超高壓往復式柱塞泵廣泛用于水力破拆系統、水刀切割、農業灌溉等領域，在超高壓范圍內，填料式密封失效，因此大多采用迷宮密封方式。迷宮密封中，影響密封效果即泄漏量的因素有很多，包括密封入口壓力、密封間隙、迷宮密封槽數量、密封槽尺寸（如角度、間距等）等［1-2］。對迷宮密封結構進行優化，降低迷宮密封的泄漏量，是往復式柱塞泵設計的重要環節。使用計算流體動力學（CFD）方法對迷宮密封結構進行優化計算，需要根據計算結果反復修改迷宮密封結構，優化計算極為耗時，而且該方法不易獲得全局最優解［3］。遺傳算法（Genetic Algorithm，GA）是一種不需要具體函數形式的非數值優化算法， 可以尋得全局最優解，適合于離散變量的優化問題。但遺傳算法優化過程中需要大量的數值計算，優化效率低［4］。而響應面法（Response Surface Methodology，RSM）使用試驗設計（Design of Experiment，DOE）方法對參數設計點集合進行試驗（仿真試驗），從而得到優化目標和約束的響應面模型，可以替代CFD的反復仿真計算，計算效率得到提高［5-7］。本文以某型號的往復式柱塞泵迷宮密封系統為對象，對迷宮密封進行了參數化建模，采用神經網絡響應面模型，并應用遺傳算法進行優化計算，得到了設計空間范圍內的全局最優解。通過優化計算，能有效降低迷宮密封系統的泄漏量。

1 迷宮密封優化模型

本文研究的迷宮密封系統位于超高壓柱塞泵的液力端，如圖1（a）所示。柱塞向左側進程時，在銅套內部產生高壓水，銅套與柱塞之間留有極小的間隙，在銅套上開出迷宮密封槽，高壓水通過這些迷宮密封槽時，會消耗壓力勢能，達到減少泄漏的目的。迷宮密封參數化結構示意圖如圖1（b）所示。A、B代表密封槽角度，H為密封槽高度，L為2個槽間距，W為密封槽頂部寬度，G為銅套與柱塞間隙，共計6個參數。

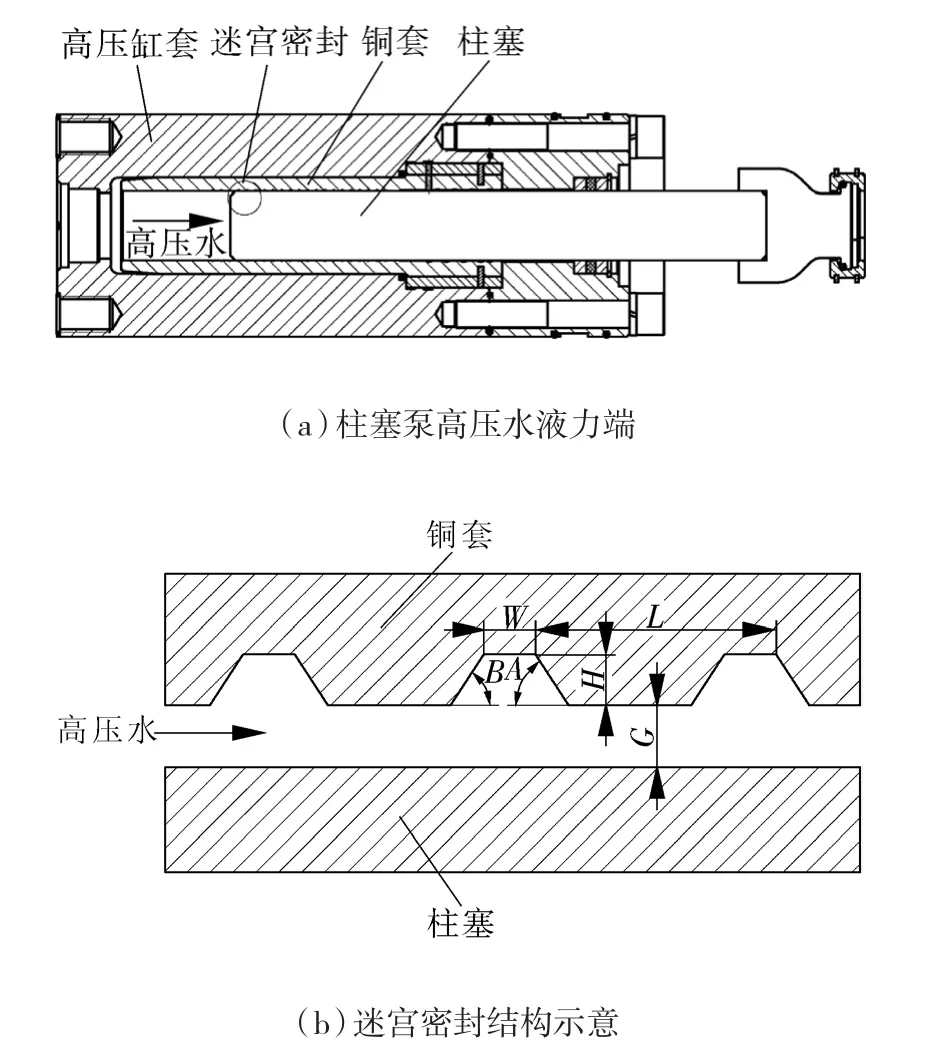
圖1 柱塞泵迷宮密封系統結構Fig.1 The structure of piston pump labyrinth seal system

1.1 迷宮密封的設計參數

本次優化設計采用的迷宮密封設計參數的初始尺寸及各參數設計空間見表1。

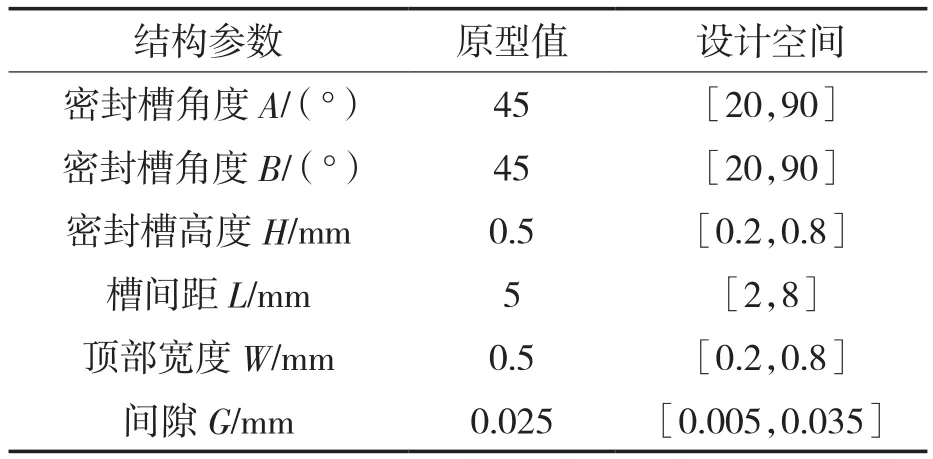
表1 迷宮密封結構原型尺寸及結構參數設計空間Tab.1 Labyrinth seal structure original size and design space of each parameter

1.2 CFD計算模型

為計算迷宮密封密封泄漏量，本文對對迷宮密封系統的流場進行了CFD分析。CFD計算的幾何模型選取迷宮密封的原型結構，該迷宮密封系統總長100 mm，密封溝槽數目為20個。劃分的網格經過網格無關性驗證，確定了最終CFD計算使用的的網格數目為55.8萬。計算使用的部分網格如圖2所示。

圖2 宮密封密封CFD計算網格（僅展示部分網格）Fig.2 The grids for CFD calculation of labyrinth seal(Only part of the grids is shown)

迷宮密封內的介質流動可以認為是穩態的湍流流動，CFD計算采用的湍流模型為SST k-omega模型。工作介質為純水，其密度為998 kg/m3，動力粘度為0.001 003 Pa·s，工作溫度為25 ℃。計算的邊界條件及設置見表2。

表2 邊界條件及設置Tab.2 Configuration of boundary conditions

為了驗證CFD計算結果，將CFD計算的迷宮密封泄漏量與理論計算公式進行了對比。迷宮密封泄漏量理論計算計算公式［8］：

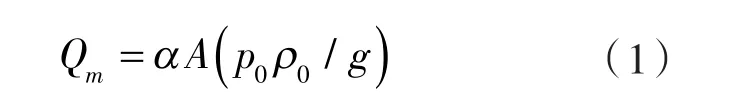
式中 Qm——泄漏量，kg/s；

α —— 流量系數，工程上流量系數一般取0.6～0.8，本文取 0.7；

A ——密封間隙面積，m2；

p0——入口壓力，MPa；

ρ0——入口介質密度，kg/m；

g ——重力加速度，m/s2， g=9.81 m/s2。

入口壓力從80 MPa到160 MPa變化。CFD計算結果與理論計算結果如圖2所示。

由圖3可知，CFD計算結果與式（1）計算結果趨勢一致，誤差為1.6%，說明本文使用的CFD模型是準確可靠的。

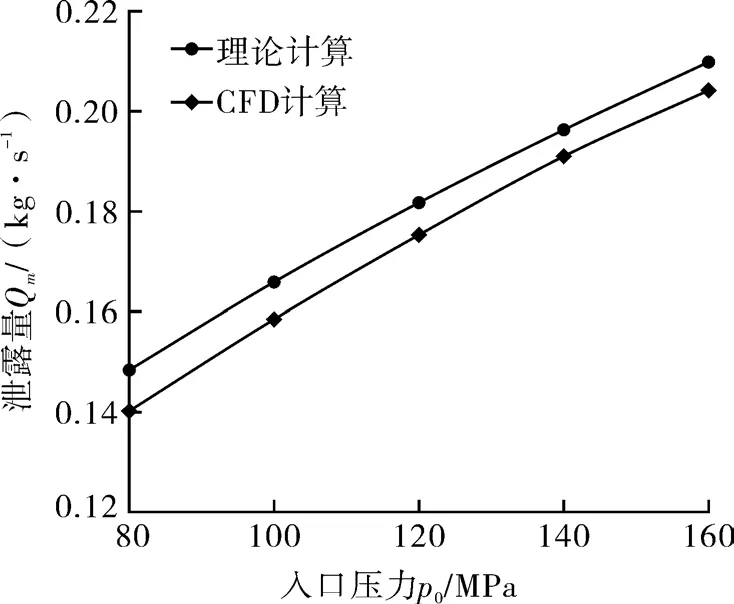
圖3 CFD計算結果與理論計算結果對比Fig.3 Comparison of CFD results and theoretical calculation results

2 神經網絡響應面模型

2.1 試驗設計和神經網絡響應面

在構造響應面模型之前，應進行試驗設計（Design of Experiment，DOE）。試驗設計通過合理選擇樣本點的數量和樣本點在設計區間內的分布，制定CFD仿真方案。拉丁超立方（Latin Hypercube Design，LHD）試驗設計是由MCKAY等提出的一種試驗設計方法，該方法具有有效的空間填充能力，而且一個設計參數的每個水平只被研究一次［9-10］。（本文根據表1所示的設計參數和以泄漏量為輸出參量，采用拉丁超立方法得到的試驗設計結果見表3。

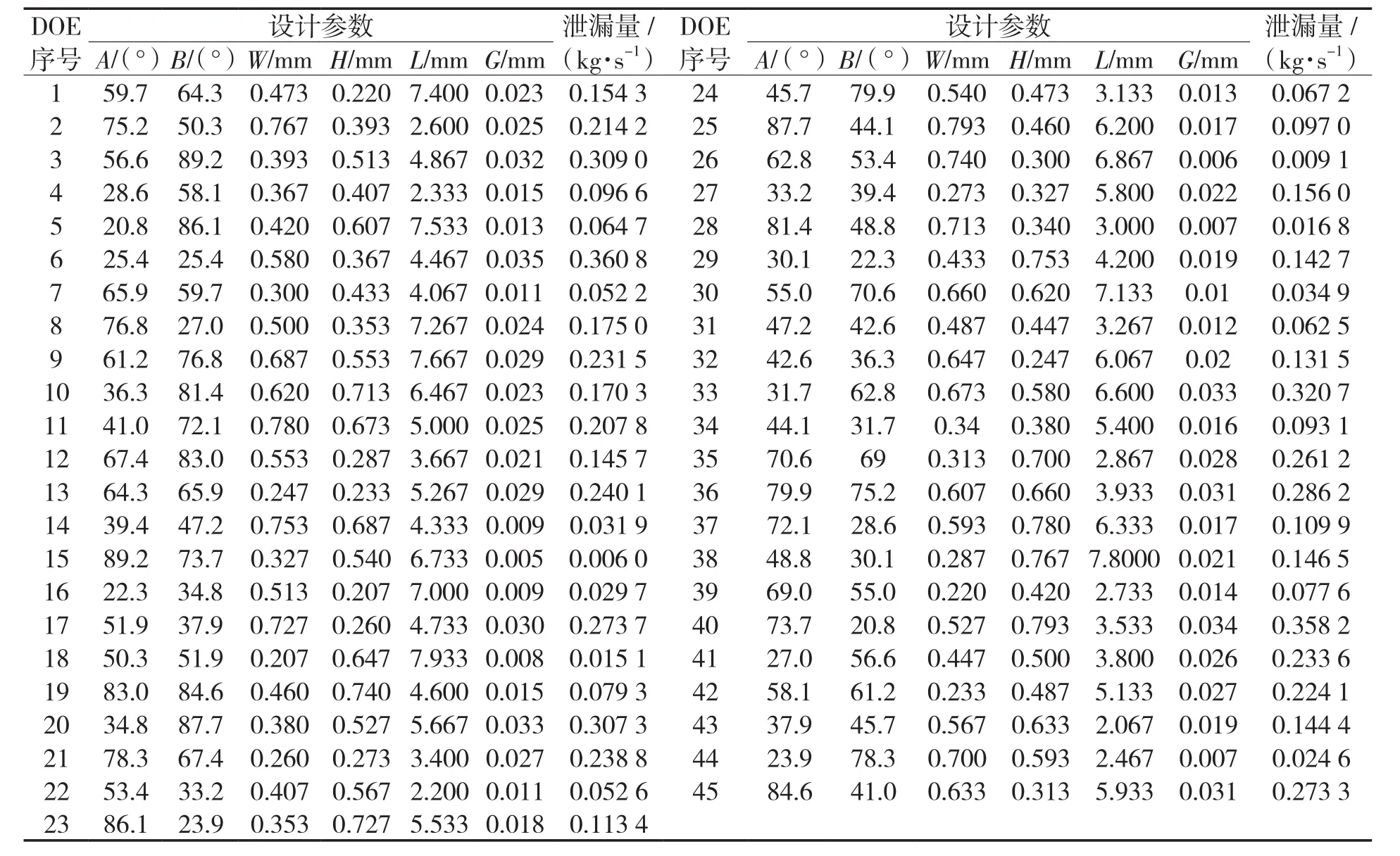
表3 拉丁超立方試驗設計結果Tab.3 The result of LHD DOE

樣本點的輸出參數泄漏量采用CFD方法計算。響應面法基于試驗設計和數理統計理論，其依靠目標函數本身的性質確定最優解，適合處理非線性數據。傳統的響應面采用二次多項式函數形式，通過試驗樣本解出出多項式系數，只能構建二次近似模型。而神經網絡響應面屬于多層前饋網絡，包含有輸入層、隱含層和輸出層，同層單元之間互不相連［11-17］。神經網絡模型示意如圖4所示。

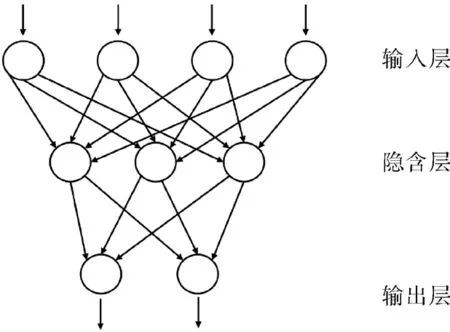
圖4 神經網絡示意Fig.4 Schematic diagram of neural network

本次研究采用了多輸入、單隱含層和單輸出的三層神經網絡模型構建了響應面模型。為了對響應面準確度進行檢驗，采用決定系數（R2）和均方根誤差（Root Mean Square Error，RMSE）作為驗證準則［18］，其定義如下：

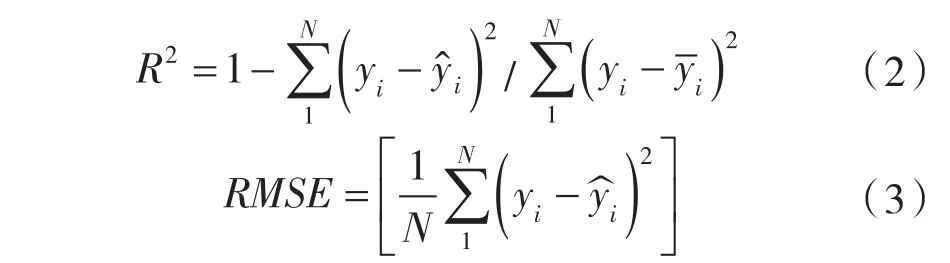
N ——檢驗樣本點數目。

R2愈接近1、RMSE愈小，響應面的擬合程度越好。在試驗設計點的間隔中，增加數個新點作為檢驗樣本點，本文通過對30組檢驗樣本點的計算得到：R2=0.999 11，RMSE=0.007 049 kg/s，說明神經網絡響應面模型的擬合精度較高，滿足優化需求。

圖5示出了迷宮密封泄漏量與各設計參數的響應面模型。

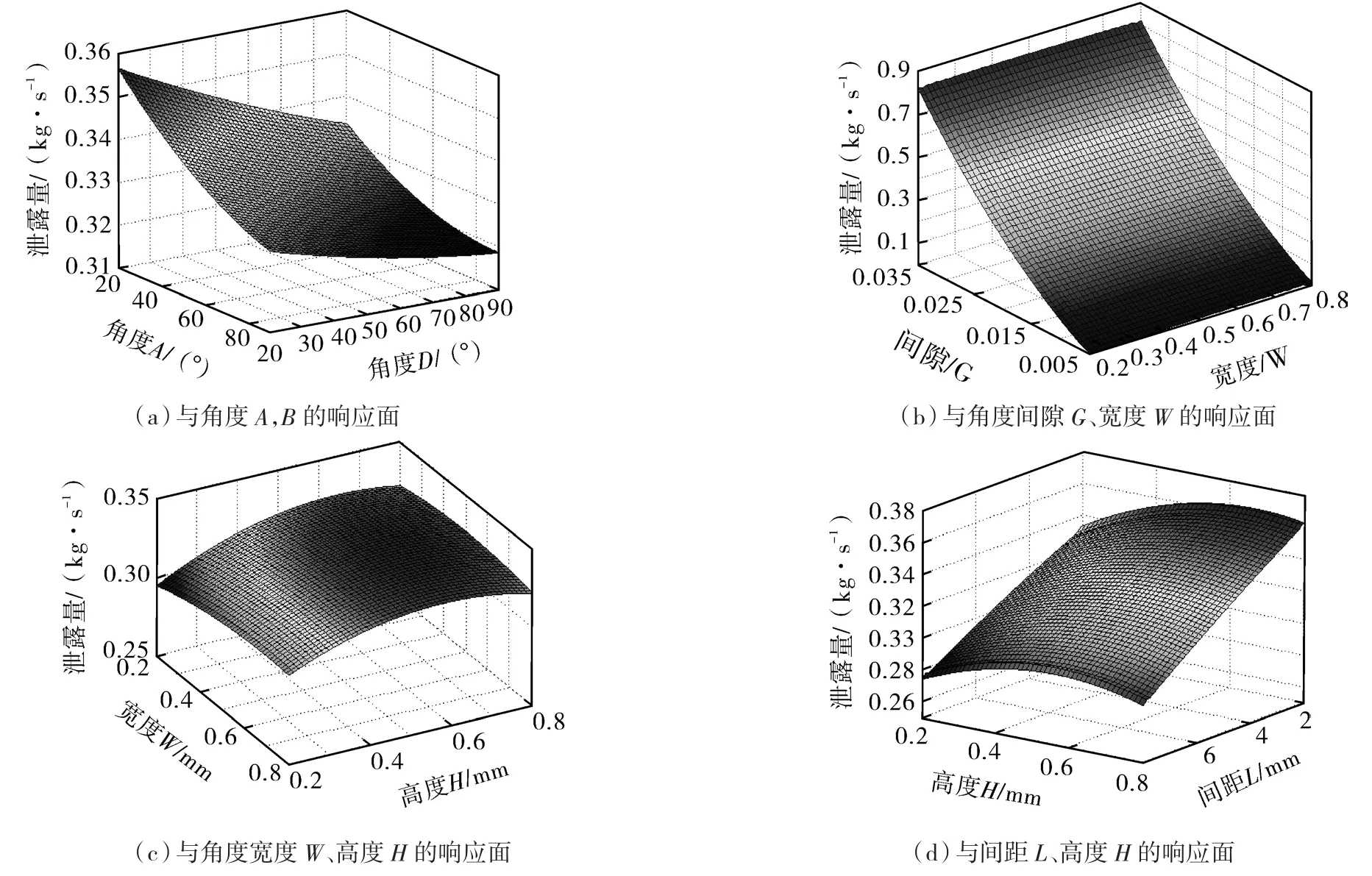
圖5 泄漏量與各設計參數的響應面Fig.5 The response surface of leakage to each design parameter

由圖5可知，迷宮密封泄漏量的影響因素中間隙G的影響最大；角度A比角度B的影響大；迷宮密封槽的高度與寬度對泄漏量影響較小，相比之下，密封槽間距對泄漏量影響較大。各參數對泄漏量的敏感度見表4。

表4 各參數對泄漏量敏感度Tab.4 Pie chart of sensitivity of each parameter to leakage

2.2 基于遺傳算法的優化計算

遺傳算法（Genetic Algorithm，GA）通過對生物自然選擇和進化的模擬進行隨機搜索，并且不需要具體的函數形式就可以獲得全局最優解。其核心思想是：通過初代種群的的復制、交叉和變異來產生下一代種群［19-24］。本文采用的遺傳優化算法的流程如圖6所示。遺傳算法需設置的主要參數有種群數量、種群代數、變異概率、交叉概率及收斂準則。種群數量對遺傳算法的性能影響較大，種群數量太小容易產生較大的采樣誤差，太大的種群數量會占用大量的計算資源；種群代數即迭代次數，目前其取值主要依靠經驗或試驗；變異概率用來控制種群中發生變異行為的個體的數量，從而使種群保持一定的多樣性，取值范圍在0～0.5之間，變異概率過大，會對解產生比較大的破化性，而且容易丟失掉最優解，變異概率太小，會使算法收斂速度變慢；交叉概率用來控制種群中發生交叉行為（2個父代個體的部分結構加以替換重組而生成新個體）的個體的數量，取值范圍在 0～1之間［25］。

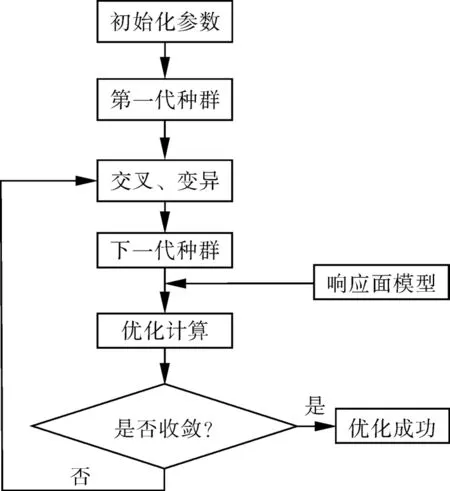
圖6 遺傳算法優化流程Fig.6 Flow chart of genetic algorithm optimization

綜合考慮本文研究的迷宮密封結構的實際工程情況，遺傳算法主要參數設置見表5。

表5 遺傳算法主要參數設置Tab.5 Configuration of main parameters of genetic algorithm

3 優化結果

本文針對迷宮密封結構的6個參數為設計變量，以泄漏量最小為優化目標，經過試驗設計，建立了神經網絡響應面模型，應用遺傳算法對迷宮密封結構進行了優化計算，并對優化后的迷宮密封結構進行了CFD計算驗證。優化結果及CFD驗證結果見表6。

表6 優化結果及CFD驗證Tab.6 The result of optimization and its CFD verification

由表6可知，基于響應面的優化結果與CFD驗證結果誤差為4.32%，說明響應面模型具有良好的準確可靠性。通過優化計算，迷宮密封的泄漏量由原型的0.197 9 kg/s降至了0.006 012 kg/s，極大改善了密封性能。

4 結語

針對某型超高壓往復式柱塞泵，本文提出了一種CFD方法、響應面模型和遺傳算法相結合的迷宮密封結構優化設計方法。通過對響應面模型的分析，可知影響迷宮密封系統的泄漏量的因素中間隙的比重最大，其次是密封槽角度、間距、寬度和高度。優化后的迷宮密封系統的泄漏量降幅極大，提高了迷宮密封的可靠性。將優化結果與CFD計算結進行了比較，表明優化模型具有較高精度，可以為超高壓柱塞泵迷宮密封系統的設計優化提供可靠的參考。