一種非線性寬頻壓電能量收集系統的動力學特性分析

劉久周 張鳳玲 辛健強 王潤 董永朋 屈強

摘要： 提出了一種基于同步開關電路的非線性寬頻壓電能量收集器，并利用高階諧波平衡法對能量收集系統的頻域響應、能量輸出功率及其影響因素等內容展開了理論研究，同時利用Hill法對系統的穩定性進行了分析。研究結果表明在基于同步開關電路的能量收集系統中引入副梁，可以大大拓寬能量收集系統工作頻帶;適當減小同步開關電路的電容比，雖然會降低能量收集系統在共振峰附近的能量收集能力，但可以拓寬系統的工作帶寬;能量收集系統的工作帶寬隨副梁與質量塊間初始間隙的減小以及副梁剛度的增大而拓寬，可根據振動能量源頻率帶寬及能量的頻域分布規律，對系統關鍵參數進行匹配設計，以獲得更好的能量收集效果。

關鍵詞： 振動能量收集; 非線性; 同步開關電路; 高階諧波平衡法; 動力學特性

中圖分類號： TN712+.5; O322? ? 文獻標志碼： A? ? 文章編號： 1004-4523（2021）03-0567-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.014

引? 言

壓電能量收集系統以壓電材料作為媒介，將系統中結構振動的機械能轉化為電能，進而通過外接能量收集電路將產生的電能收集起來。收集的能量可以為系統內的電子元件供能，降低系統對電源的需求，因此壓電能量收集系統在機械、電子等領域具有廣闊的應用前景，受到了研究人員的廣泛關注[1]。

早期的被動線性壓電能量收集系統，存在能量收集效率低、工作帶寬較窄、對振動環境變化敏感等缺陷[2?3]。針對被動線性壓電能量收集系統的缺陷，近年來以同步開關電路為代表的半主動能量收集電路成為研究人員關注的熱點。基于壓電材料的同步開關能量收集（Synchronized Switch Harvesting， SSH）技術是一種典型的半主動壓電能量收集技術，最早由Richard等提出[4]。其工作原理為：在粘貼于結構上的壓電片兩電極之間連接有同步開關電路，壓電片隨結構的振動發生彈性形變，當壓電片電極電壓達到極值時，電路中的同步開關元件自動迅速閉合，電極電壓方向發生“翻轉”，然后開關又迅速斷開，這使得壓電片電極之間始終保持較高的電壓水平，進而使其收集能力相對于被動的壓電能量收集系統得到大大提升。

目前應用最廣泛的同步開關能量收集器是基于電感元件的同步開關能量收集器（Synchronized Switch Harvester Based on Inductor， SSHI），電路中的電感元件可以在一定程度上增大壓電片的電壓幅值，從而提高系統的能量收集效果，整個能量收集系統通過集成電路的方式實現，實現起來也較為方便[5]。但SSHI電路中壓電片電壓幅值受限于電路的品質因子，而電路品質因子又是電路自身的固有特性，取值會受到限制，因此SSHI技術的能量收集效果也將受限于電路的品質因子[6]。Ji等[7]在研究中發現，利用負電容元件替換電路中的電感元件，形成的基于負電容的同步開關能量收集器（Synchronized Switch Harvester Based on Negative Capacitor， SSHNC），不僅能保證電壓的“翻轉”和放大，還能避免SSHI技術的能量收集效果受限于電路自身品質因子的缺點。在此基礎上，研究人員又開發了自供能同步開關能量收集電路[8?9]，即利用收集到的電能給開關電路提供能量，實現了電路系統能量上的自給自足，擴大了同步開關能量收集技術的適用范圍。

為了拓寬壓電能量收集系統的工作頻帶，研究人員試圖在能量收集系統中引入非線性因素，利用非線性系統動力學的特性，在更寬的頻帶內獲得較好的能量收集效果。Liu等[10]和Zhao等[11]基于懸臂梁模型，在線性壓電能量收集系統中引入沖擊梁，使振動主梁與沖擊梁構成一個雙線性系統，拓寬了能量收集系統的工作帶寬。Wu等[12]利用一個兩自由度模型研究了三次非線性對線性壓電能量收集電路的影響。文獻[13?15]利用磁場作用在線性壓電能量收集系統中引入雙穩態非線性，采用時域分析方法對能量收集系統動力學特性進行了分析，并利用懸臂梁系統對分析結果進行了試驗驗證。Wang等[16]以懸臂梁為模型，在線性壓電能量收集系統中同時引入雙穩態和雙線性因素，其研究表明雙線性因素可以使雙穩態壓電能收集系統的能量收集效果進一步獲得提升。

分析發現，現有文獻中的研究大多是在線性壓電能量收集電路中引入非線性因素，并利用時域分析方法或試驗研究的方法對能量收集系統的動力學特性進行研究。而由于同步開關電路自身的非線性特點等因素，在效果更好的同步開關能量收集系統中引入非線性因素，進一步提升同步開關電路工作帶寬和能量收集效果的相關研究鮮有報道。本文提出了一種基于同步開關電路的非線性寬頻壓電能量收集系統，在同步開關能量收集系統中引入具有沖擊作用的副梁，探索在更寬的頻帶內獲得較好的能量收集效果的方法，并從理論上對能量收集系統的動力學特性進行了研究。

1 能量收集系統動力學模型

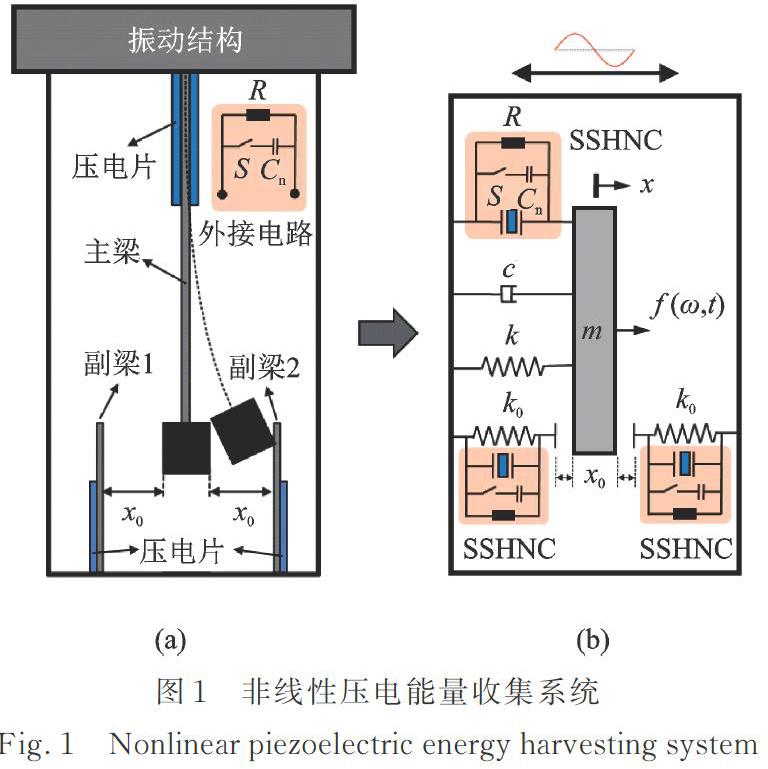
壓電能量收集系統如圖1（a）所示：在與振動結構相連的剛性框架內設置一個懸臂梁（后文稱之為“主梁”），懸臂梁與其自由端的剛性質量塊構成“彈簧?振子”系統。懸臂梁自身質量相對于質量塊可以忽略，懸臂梁主要提供“彈簧?振子”系統的剛度。在剛性框架中與質量塊兩側距離為的位置分別再設置一個懸臂梁（后文分別稱之為“副梁1”和“副梁2”），當結構發生振動時，剛性框架隨之運動，連接質量塊的主梁也隨之振動，當振動幅值足夠大時，副梁與質量塊發生接觸并隨之振動（忽略碰撞造成的能量損失）。副梁質量相對于質量塊也可以忽略，其主要作用為在與質量塊發生接觸時改變“彈簧?振子”系統的剛度。在主梁及副梁根部位置分別粘貼有壓電片，壓電片的正壓電效應可以將懸臂梁因振動產生的應變能轉化為電能，進而通過壓電片電極之間外接的同步開關電路收集起來，以實現對結構振動能量的收集。

由于三個懸臂梁的質量相對于質量塊可以忽略，且壓電片粘貼在梁根部，壓電片主要感受懸臂梁一階模態振型的應變，能量收集系統主要收集梁的一階振動能量，這樣，對圖1（a）中的能量收集系統動力學特性的分析可以轉化為對圖1（b）所示系統的分析。圖1（b）中為質量塊質量，為主梁的剛度，為副梁的剛度，為機械阻尼系數，為副梁與質量塊之間的初始間隙。在質量塊振動的過程中，除了受到激振力的作用，還會受到壓電片產生的機電耦合作用力，以及副梁產生的作用力，因此，整個能量收集系統的動力學方程可以表示為

如圖1（b）所示，在壓電片兩電極之間連接一個同步開關（用表示，實際中利用電路實現），以及一個負電容元件（表示，實際中通過模擬電路實現）。同步開關電路在實現電壓方向“翻轉”同時，還能實現電壓幅值的“放大”，進而提升了與開關元件并聯支路的能量收集能力，這種同步開關電路被稱為基于負電容的同步開關能量收集器（SSHNC）。

對于SSHNC系統，在一個振動周期中，壓電片電極電壓與振動位移之間的關系如圖2所示。在實際中，同步開關的作動時間一般遠小于結構振動周期，即在一個振動周期中，開關處于閉合狀態的時間遠小于開關處于斷開狀態的時間[5]。由壓電傳感方程可知[6]，同步開關閉合前后的電壓幅值，以及結構振動幅值之間存在如下關系

式中? 為壓電片的內置電容，為壓電片的力系數，實際中這兩個參數均可通過試驗測得[6]。為了方便，在進行理論分析時可以忽略開關閉合的瞬間[17?19]，結合式（2）及開關電路的工作原理可得SSHNC電極電壓的表達式為

式中? 表示符號函數，為SSHNC電路中負電容值的大小與壓電片內置電容值之比，即

從表達式（2）可以看出，電壓的幅值與成正比，且為結構振動位移及振動速度的非線性函數，因此具有SSHNC的機電耦合系統為典型的非線性系統，文獻[6?7]的相關實驗研究驗證了式（3）的合理性。在式（3）中，由于，因此等號右邊第一項的絕對值始終大于或等于第二項的絕對值，也就是說電壓的方向始終與結構的振動速度的方向相反。由此可見，在收集量的同時，SSHNC還將產生一個阻礙“彈簧?振子”系統振動的機電耦合作用力，且力的大小與壓電片電極電壓成正比[7]，其數學表達式為

由同步開關電路的工作原理可以看出，同步開關電路不同于以往基于電路諧振的線性能量收集系統[2]，電路不需要與系統進行“調諧”，因此基于同步開關電路的能量收集系統具有更寬的工作頻帶。

當質量塊與副梁接觸時，副梁會對質量塊產生反作用力。由于副梁根部粘貼有壓電片并連接有能量收集電路，除了副梁自身剛度產生的反作用外，壓電片也會對副梁產生機電耦合作用力，而該力最終也將通過副梁傳遞到質量塊上。因此，共包含兩部分，其表達式為

式中? 為副梁自身剛度產生的作用力，該作用力具有“雙線性”的特點（如圖3所示），其數學表達式如下式所示

文獻[11]的相關實驗研究驗證了式（7）的合理性。

為壓電片通過副梁對質量塊的非線性機電耦合作用力，其大小與副梁根部壓電片電極電壓成正比，數學表達式為：

為使研究具有更廣泛的意義，對能量收集系統的非線性機電耦合動力學方程（1）進行無量綱化，無量綱原則為

將上述無量綱原則帶入式（1）可得能量收集系統的無量綱非線性機電耦合動力學方程為

其中，無量綱非線性力數學表達式分別為：

2 頻域分析方法

2.1 非線性系統頻域響應計算方法

方程（10）含有多種非線性因素，其動力學特性的分析（特別是頻域響應的求解）存在一定的難度。雖然直接積分法求解非線性動力學方程的計算精度很高，但計算效率較低，如果采用直接積分法獲得系統的頻響曲線，會耗費大量的計算時間。諧波平衡法作為一種經典的非線性系統求解方法具有很多優勢，幾乎能夠處理包括幾何非線性、接觸非線性、材料非線性在內的各種強/弱非線性問題，是一種高效、可靠的計算方法[17?19]。但是，對于強非線性系統，只保留一階諧波的諧波平衡法很難保證求解精度[20]，由此發展了保留更多諧波階次的高階諧波平衡法（Multi?Harmonic Balance Method， MHBM）。

任意離散非線性系統的自由振動方程可以表示為如下形式

式中? 為系統所受的非線性力。首先將系統的周期解展開成傅里葉級數的形式

式中? 為計算過程中保留的諧波階次，保留的諧波階次越多，計算結果越精確，計算量也會隨之上升。

將非線性系統振動幅值的傅里葉系數寫成向量的形式為

同理，將系統激振力及非線性力展開成傅里葉級數的形式：

激振力及非線性力的傅里葉系數的向量形式為：

將式（11）和（13）代入式（10）中，利用伽遼金過程將非線性系統的動力學微分方程組從時域轉換到頻域，得到非線性系統的頻域代數方程組

式中? 為動剛度矩陣，其表達式為：

其中矩陣子塊表達式為

對于較為復雜的系統，利用高階諧波平衡法（MHBM）求解時，當保留的諧波階次大于3（即）時，方程組（21）的解析形式難以直接寫出，此時可以采用Cameron等[20]提出的時頻轉換（Alternation Frequency/Time Domain Method， AFT）技術，利用快速傅里葉變換程序完成分析過程中的正逆傅里葉變換。

在使用牛頓迭代法對非線性代數方程組（21）進行求解時，為確保非線性求解過程的收斂性，可以引入弧長延拓技術。弧長延拓技術包括“預測步”和“校正步”兩個基本步驟，其基本思路為：

對方程進行泰勒展開，并保留一階精度可得

式中? 為預測步的增量向量。為保證預測點與初始點之間的距離始終為，可以得到如下關系

根據式（24）和（25）可以求得預測步的增量向量。由增量向量可以獲得預測點的位置為，然后對預測點進行校正：以為中心，為半徑的圓與函數“曲線”的交點即為系統的解。因此，非線性方程組校正后的解可由以下方程確定

一般選擇合適的，并經過數次校正之后就可以獲得收斂的非線性系統的頻域響應，非線性系統頻域響應計算流程如圖4所示。

2.2 非線性系統穩定性分析方法

與線性系統不同，非線性系統可能存在不穩定的周期解，本文采用Hill法[21]對周期解的穩定性進行分析。假設非線性系統周期解受到一個擾動，則時域響應可以寫為

將代入方程（14）中，并利用諧波平衡法將時域中的非線性方程組轉化為頻域中的非線性代數方程組

對式（34）對應的特征方程進行求解，可以獲得一系列的復特征值。當系統的全部復特征值的實部都小于0時，方程的解穩定，當存在實部大于0的特征值時，方程的解不穩定。

2.3 算例分析

利用MHBM法對經典的Duffing系統的頻域響應進行求解（計算過程中保留5階諧波），并利用Hill法對解的穩定性進行分析。Duffing系統的動力學方程為

不同激勵頻率下，特征值實部如圖5所示，對應的頻響曲線如圖6所示。通過與文獻[22]中典型的Duffing系統計算結果進行對比，表明當保留足夠多的諧波階次時（保留的諧波階次數可根據非線性系統的具體性質來確定，一般諧波階次大于5即可保證足夠的求解精度），利用MHBM能夠比較精確地求解非線性系統的頻域響應，同時Hill法可以對頻域響應的穩定性進行分析，后續將利用該方法對能夠收集系統的頻域特性進行分析。

3 能量收集系統動力學特性

3.1 能量收集系統頻域響應

當副梁無量綱剛度，同步開關電路無量綱機電耦合系數（如無特殊說明，后文中取值均為0.1），電容比，無量綱激振力幅值為1，副梁與質量塊初始間隙分別為，和時，系統頻響曲線及其穩定性如圖7所示。從圖中結果可以看出，當初始間隙較大（）時，由于質量塊無法與副梁發生接觸作用，壓電片的非線性力不能使能量收集系統頻響曲線產生“歪頭”現象。隨著初始間隙的減小，質量塊將與副梁發生接觸，進而使系統頻響曲線產生向右“歪頭”的現象，且副梁與質量塊之間的初始間隙越小，頻響曲線向右“歪頭”越明顯。當初始間隙，副梁剛度分別為，和時，系統頻響曲線及其穩定性如圖8所示。可見，副梁與質量塊之間的初始間隙一定時，副梁剛度越大，頻響曲線向右“歪頭”越明顯。

初始間隙及副梁剛度一定時，當激勵頻率由小到大或由大到小變化時，系統頻響曲線將會出現非線性系統典型的“跳躍”現象（如圖9所示）。當頻率由小到大變化時，能量收集系統產生較大振幅的頻帶更寬。由于壓電片電極電壓與懸臂梁根部應變水平成正比，而能量收集效果與壓電片電極電壓正相關，因此當振動頻域由小到大逐漸變化時，副梁的存在可以拓寬能量收集系統的工作頻帶，獲得更好的能量收集效果，接下來我們將針對這種情況進行分析。

3.2 能量收集系統頻域輸出功率

能量收集系統中主梁壓電片電壓以及兩個副梁上壓電片的電壓分別用，和表示。當副梁剛度，同步開關電路電容比，副梁與質量塊初始間隙，激振力幅值為1，激振頻率為時，在兩個完整振動周期內能量收集系統中壓電片電壓，及振動位移的時域曲線分別如圖10和11所示。顯然，在整個振動周期內主梁上的能量收集系統一直具有能量收集作用，而只有當質量塊與副梁發生接觸并使副梁發生變形時，副梁上的能量收集系統才具有能量收集作用。

為了對系統的能量收集效果進行評估，定義壓電片在一個振動周期內向外電路輸出的能量與振動周期之比為能量平均輸出功率（后文簡稱“輸出功率”），其物理意義為能量收集電路在單位時間內向外輸出能量的平均值。對于壓電片，輸出功率可以表示為

式中? 為壓電片的輸出功率，為壓電片在一個振動周期內輸出的電能，為主梁的振動周期，為壓電片的無量綱內置電阻值，為外接電路中的無量綱電阻值。整個能量收集系統的總輸出功率為

由式（37）可以看出，當外接電路中的電阻值與壓電片內阻值相等時，壓電片總輸出功率最大，因此在后續分析中，均取。后續將利用輸出功率作為評價指標，對不同參數下系統的能量收集效果進行評估，進而對系統設計參數進行優化。

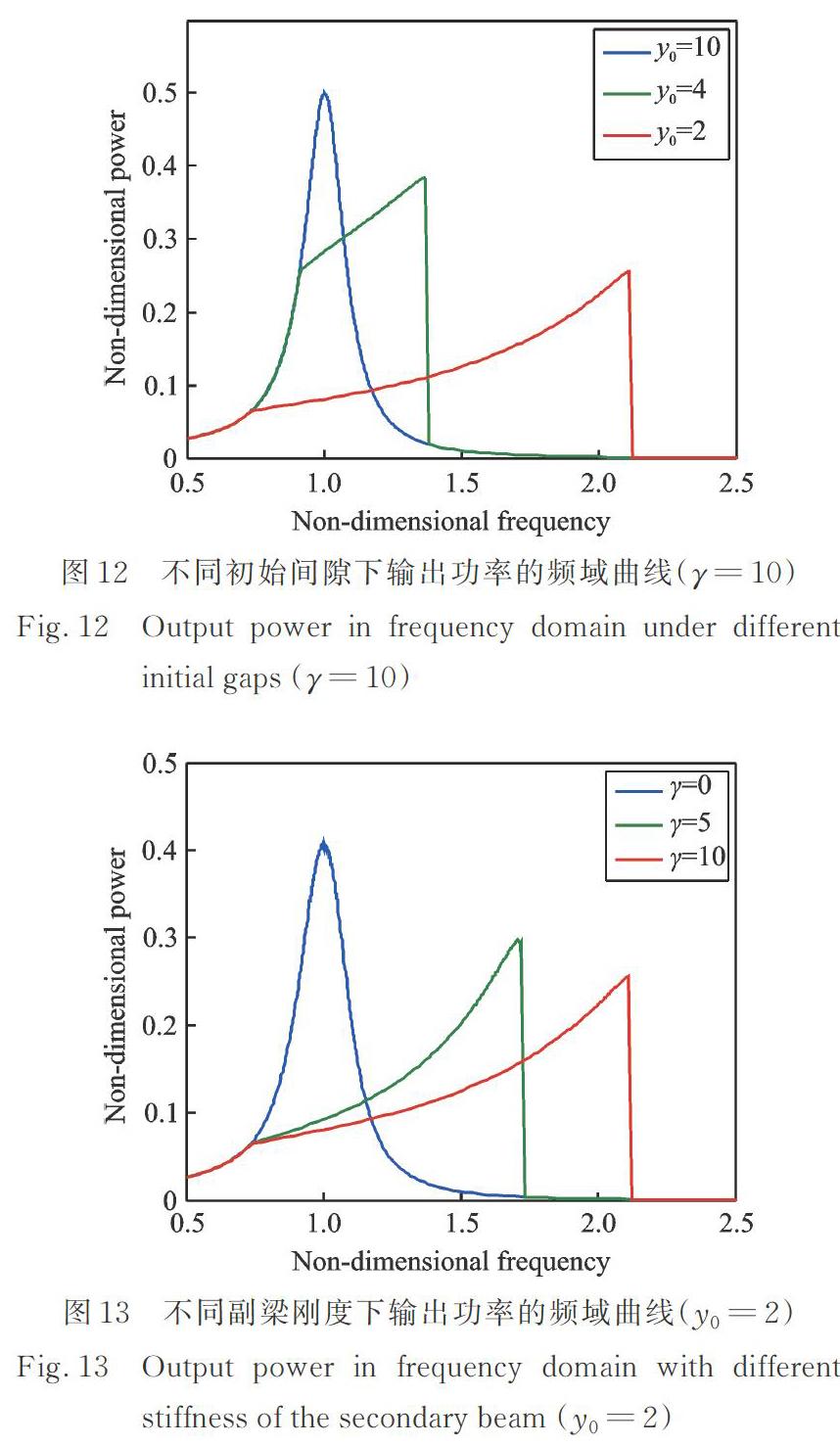
當同步開關電路電容比為，無量綱激振力幅值為1，不同初始間隙及不同副梁剛度下，系統的總輸出功率分別如圖 12和 13所示。從圖中的結果可以看出，雖然副梁會使同步開關能量收集系統在共振峰值附近的能量收集能力降低，但使得工作帶寬大大拓寬，系統在整個工作頻帶上能夠收集更多的能量。因此，在同步開關電路和副梁的共同作用下，使得該能量收集系統相比于以往的基于線性電路的雙穩態能量收集系統更加適合于寬頻域能量收集。

3.3 系統參數對能量收集效果的影響

3.3.1 同步開關電路參數對能量收集效果的影響

式（3）表明，壓電片電極電壓幅值主要取決于同步開關電路電容比，而電壓幅值直接影響能量收集系統的輸出功率，因此對輸出功率具有決定性影響。當副梁系統參數（和）一定時，不同電容比下系統頻響曲線及總能量輸出功率曲線分別如圖14和15所示。可以看出，當激振力幅值一定時，同步開關電路電容比越大，系統在共振峰附近的振動峰值越小，能量收集系統在共振峰值附近的能量收集能力越強。當電容比過大（如）時，系統振動幅值過小，質量塊與副梁無法相互接觸，副梁無法起到拓寬能量收集系統工作帶寬的作用。因此，適當減小電路中的電容比，雖然會降低系統在共振峰附近的能量收集能力，但可以拓寬系統的工作頻帶。實際中可根據能量源的頻率變化范圍來選擇同步開關電路的電容比，以兼顧能量收集系統的工作帶寬和能量收集效率。

3.3.2 副梁參數對能量收集效果的影響

取同步開關電路電容比，當副梁剛度時，初始間隙對系統的輸出功率及工作帶寬的影響規律如圖16所示。而當初始間隙時，副梁剛度對系統的輸出功率及工作帶寬的影響規律如圖17所示。可見，副梁與質量塊的初始間隙以及副梁剛度對能量收集系統工作帶寬以及輸出功率具有較大影響。副梁與質量塊的初始間隙越小，副梁的剛度越大，能量收集帶寬越寬，但最大輸出功率也會有所下降。需要指出的是，由于同步開關能量收集電路自身的能量收集能力較強[4?5]，因此即使輸出功率有所下降，同步開關電路相比于傳統的被動能量收集系統依然具有很好的能量收集效果，應根據振動環境的頻率變化范圍以及激振力幅值水平，對能量收集器進行合理的設計，進而獲得更好的能量收集效果。

副梁的無量綱剛度時，初始間隙對副梁輸出功率占系統總輸出功率的百分比的影響規律如圖18所示。當初始間隙為時，副梁剛度對副梁輸出功率占比的影響規律如圖19所示。根據分析結果可知，當初始間隙較小，副梁剛度也較小時，副梁的能量收集效果較好（占總輸出功率的10%左右）。可見，雖然主梁的輸出功率仍在能量收集系統的總輸出功率中占主導，但在特定頻帶內，副梁上布置的能量收集器也會為整個系統的能量收集帶來比較可觀的貢獻。

4 結? 論

在基于同步開關電路的壓電懸臂梁能量收集系統中引入副梁，形成一種非線性寬頻壓電能量收集系統，并利用高階諧波平衡法對系統頻域響應及能量收集效果進行了理論研究，為該非線性寬頻能量收集系統的應用提供依據。分析結果顯示：①非線性同步開關電路的引入，拓寬了傳統線性壓電能量收集電路的工作頻帶，而副梁的引入可以進一步拓寬基于同步開關能量收集系統的工作帶寬。在同步開關電路和副梁共同作用下，使得該能量收集系統相比于以往基于線性電路的雙穩態能量收集系統更加適合于寬頻域能量收集;②適當減小同步開關電路的電容比及副梁與質量塊間的初始間隙、增大副梁剛度，雖然會降低系統在共振峰附近的能量收集能力，但可以拓寬系統的工作頻帶;③實際中振動能量源往往具有寬頻特點，因此，除了保證共振峰附近的能量收集能力，還要關注一定頻帶寬度上的總能量收集效率。需結合振動能量源頻率帶寬及能量的頻域分布規律，對系統關鍵參數進行匹配設計，以獲得最佳能量收集效果。

參考文獻：

[1] Mitcheson P D， Yeatman E M， Rao G K， et al. Energy harvesting from human and machine motion for wireless electronic devices[J]. Proceedings of the IEEE， 2008，96（9）：1457-1486.

[2] Leland E S， Wright P K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload[J]. Smart Material Structures， 2006， 15（5）：1413-1420.

[3] Hagood N W， von Flotow A. Damping of structural vibrations with piezoelectric materials and passive electrical networks[J]. Journal of Sound and Vibration， 1991， 146（2）： 243-268.

[4] Richard C， Guyomar D， Audigier D， et al. Semi-passive damping using continuous switching of a piezoelectric device[C]. Smart Structures and Materials 1999： Passive Damping and Isolation International Society for Optics and Photonics， Newport Beach， CA， USA，1999：104-111.

[5] Richard C， Guyomar D， Audigier D， et al. Enhanced semi-passive damping using continuous switching of a piezoelectric device on an inductor[C]. Smart Structures and Materials 2000： Damping and Isolation， Newport Beach， CA， USA， 2000： 288?299.

[6] 季宏麗. 飛行器結構壓電半主動振動控制研究[D]. 南京： 南京航空航天大學， 2012.

Ji Hongli. Research on piezoelectric semi-active vibration control of aircraft structures[D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2012.

[7] Ji H， Qiu J， Cheng J， et al. Application of a negative capacitance circuit in synchronized switch damping techniques for vibration suppression[J]. Journal of Vibration & Acoustics， 2011， 133（4）：041015.

[8] Lallart M， Guyomar D， Jayet Y， et al. Synchronized switch harvesting applied to self-powered smart systems： Piezoactive microgenerators for autonomous wireless receivers[J]. Sensors and Actuators A： Physical， 2008， 147（1）： 263-272.

[9] Eltamaly A M， Addoweesh K E. A novel self-power SSHI circuit for piezoelectric energy harvester?[J]. IEEE Transactions on Power Electronics， 2017，32（10）：7663-7673.

[10] Liu S， Cheng Q， Zhao D， et al. Theoretical modeling and analysis of two-degree-of-freedom piezoelectric energy harvester with stopper[J]. Sensors and Actuators A： Physical， 2016， 245：97-105.

[11] Zhao D， Wang X， Cheng Y， et al. Analysis of single-degree-of-freedom piezoelectric energy harvester with stopper by incremental harmonic balance method[J]. Materials Research Express， 2018，5（5）：055502.

[12] Wu Yipeng， Ji Hongli， Qiu Jinhao， et al. A 2-degree-of-freedom cubic nonlinear piezoelectric harvester intended for practical low-frequency vibration[J]. Sensors and Actuators A： Physical， 2017， 264： 1?10.

[13] Gao Y J， Leng Y G， Fan S B， et al. Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet[J]. Smart Materials and Structures， 2014，23（9）：1-14.

[14] Lan Chunbo， Qin Weiyang. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester[J]. Mechanical Systems and Signal Processing， 2017，（85）：71-81.

[15] Fang Hongbin， Wang K W. Piezoelectric vibration-driven locomotion systems——Exploiting resonance and bistable dynamics[J]. Journal of Sound and Vibration， 2017，391： 153-169.

[16] Wang Chen， Zhang Qichang， Wang Wei. Low-frequency wideband vibration energy harvesting by using frequency up-conversion and quin-stable nonlinearity[J]. Journal of Sound and Vibration， 2017， 48（2）： 169-181.

[17] Liu Jiuzhou， Li L， Huang X， et al. Dynamic characteristics of the blisk with synchronized switch damping based on negative capacitor?[J]. Mechanical Systems and Signal Processing， 2017，95： 425-445.

[18] Liu J， Li L， Fan Y. A comparison between the friction and piezoelectric synchronized switch dampers for blisks?[J]. Journal of Intelligent Material Systems and Structures， 2018， 29（12）：2693-2705.

[19] Liu Jiuzhou， Li Lin， Fan Yu， et al. A modified nonlinear modal synthesis scheme for mistuned blisks with synchronized switch damping?[J]. International Journal of Aerospace Engineering， 2018， 2018： 8517890.

[20] Cameron T M， Griffin Jerry H. An alternation frequency/time domain method for calculation the steady-state response on nonlinear dynamic system?[J]. Journal of Applied Mechanics， 1989， 56（1）：149-154.

[21] Zhou B， Thouverez F， Lenoir D. Essentially nonlinear piezoelectric shunt circuits applied to mistuned bladed disks[J]. Journal of Sound and Vibration， 2014， 333（9）： 2520-2542.

[22] Laxalde D. Stability analysis of periodic orbits in the framework of Galerkin approximations?[J]. 2011：hal-00655521.

作者簡介： 劉久周（1988?），男，工程師。電話：13401177057; E-mail： liujiuzhou123@126.com