基于粒子群算法的火電單元機組模型參數辨識

宋莉莉 劉婷 陳莉

（1.昌吉學院物理系 新疆維吾爾自治區昌吉回族自治州 831100）（2.新疆新檢質量有限公司 新疆維吾爾自治區烏魯木齊市 830000）

1 引言

目前，在我國大部分地區仍然是火力發電占據著主要的位置。隨著現代科技的快速發展，我國國民經濟對整個電力的需求量與日俱增，同時對電力供應的可靠性、穩定性要求也越來越嚴格，一方面需要保證機組的安全運行；另一方面又要保證火電廠中發電機組的有功功率能及時跟上電網負荷的變化[1]。在當今社會，節能減排是整個地球公民所關心的問題，隨著國內外大容量機組的快速發展，我國在以300MW 容量發電機組為骨干的基礎上，開展了600MW以及超臨界、超超臨界甚至更大容量的發電機組的建設和使用[3]。就對于火電單元機組來說，想要讓整體系統的質量、效率得到一定的保障，就需要建立準確的系統模型。隨著這方面的不斷發展，熱工過程模型辨識的方法有很多，其中就包括最小二乘法、遺傳算法、階躍響應法[4]。我國的火電機組一直在不斷地優化[5]，現今機組設備增大、參數增多，由于種種現實問題使得很多科研實驗都沒有辦法進行，在這種大環境下，建立系統模型就顯得格外重要。

粒子群算法（Particle Swarm Optimization，簡稱PSO）是智能優化算法，它的出現在一定范圍內掀起了一陣浪潮。粒子群算法具有原理簡單、所需參數少、應用廣泛等優勢[6]。用于求解更多更復雜的問題，仍是一個研究的熱點。

本文是以再熱汽溫系統為研究對象，首先建立模型，然后利用PSO 算法對系統進行參數辨識，得出粒子群算法可以很有效地對系統模型進行參數辨識，并且有操作容易，易理解，速度快并且辨識精度高等優點。

2 粒子群算法介紹

2.1 粒子群算法基本原理

在1995年，粒子群算法（PSO）正式誕生，是由兩位學者Kennedy 和Eberhart 提出[7]。該算法通過粒子之間的信息共享機制，利用并行搜索原理，找到最優值。主要特點是原理簡單、參數少、收斂速度快。具體過程為：隨機初始化一群粒子，每個粒子按一定的速度飛行。在飛行中粒子會根據自身以及種群經驗動態調整自身的速度和位置。

表1：仿真結果對比

圖1：基本粒子群算法流程圖

圖2：辨識問題與優化問題轉化圖

圖3：減溫水擾動下再熱汽溫的階躍響應曲線

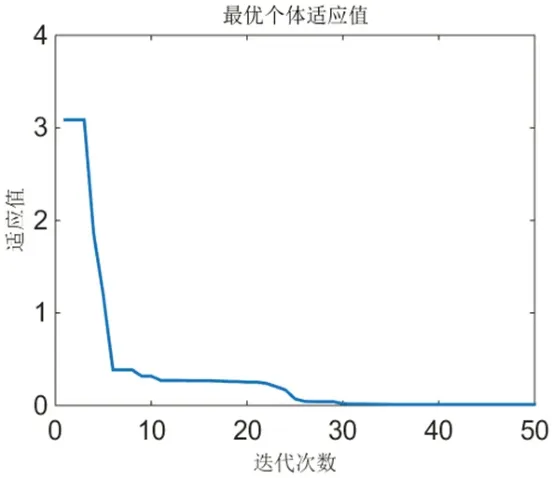
圖4：最優個體適應值

圖5：優化曲線

設在D 維搜索空間中，種群規模為m，這個群體中的各個粒子都有自己的飛行速度和方向。設第i 個粒子的位置：xi=(xi1,xi2,…,xid)

速度為：vi=(vi1,vi2,…,vid），粒子個體極值：pi=(pi1,pi2,…,pid)；全局極值：pg=(pg1,pg2,…,pgd)

更新速度公式：

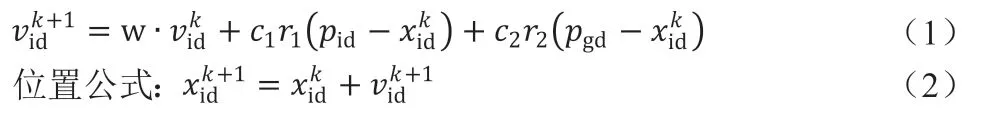
其中，i=1,2,…,m,d=1,2,…D,k：迭代次數；w：慣性權重；r1?[0 1]，r2?[0 1]；加速常數：c1=c2。算法流程圖如圖1 所示。

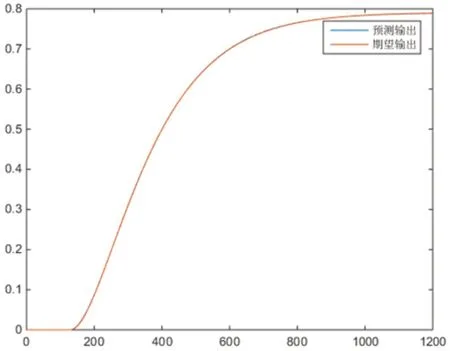
圖6：再熱蒸汽溫度控制系統模型辨識結果

2.2 函數測試

本文中用粒子群算法和遺傳算法分別對函數f=x·sinx·cos2x-2x·sin3x 進行了優化，優化結果對比如表1 所示。

粒子群算法與遺傳算法進行比較，發現粒子群算法的運行速度快于遺傳算法。由此可以知道粒子群算法對函數優化具有非常好的尋優能力，所以本文將模型參數辨識問題轉化為函數優化問題，并用粒子群算法來對再熱蒸汽溫度控制系統進行研究。

2.3 基于粒子群算法的辨識原理

系統辨識即根據輸入和輸出數據，利用某一準則確定等價的模型。進行研究的時候，首先要根據實驗得出一個模型，將實驗結果放入此模型來進行預測，然后比較計算所得值與測試所得數據，若兩者之間相差較大，就說明模型與事實不符，對模型進行修改；如果兩者之間相差很小，就認為此模型符合事實，從而將它運用于實驗。其轉化過程如圖2 所示。

利用粒子群算法進行系統辨識假設：

粒子維數：[k,τ,t1,t2,…tn]，以數據y 為樣本，根據輸出y'取適應度函數：具體步驟如下：

Step1 m=40,k?[0.01 100],ti?[0.1 100],τ?[0～300],c1=c2= 1.4962,T=50 Step2 數據初始化：pi,pg,vi,xi Step3 根據計算適應度值Step4 更新pbest,pgbest Step5 更新速度位置公式Step6 IF T<50 continue step3；else stop

3 基于粒子群算法的火電單元機組模型參數辨識

大型火電機組是由鍋爐、汽輪機和發電機為主體的設備群。本文以再熱蒸汽溫度控制系統作為研究對象，將系統辨識問題轉化為優化問題，并采用粒子群優化算法對火電單元機組進行了研究。

3.1 再熱蒸汽溫度控制系統的模型構建

影響再熱器出口汽溫的因素很多，主要為蒸汽流量、煙氣量和減溫水量三方面。在減溫水流量擾動下溫度的響應曲線如圖3 所示。

再熱汽溫的特點為有延遲、有慣性、有自平衡能力。傳遞函數表示為：

式（3）中：t：時間常數；k:放大系數；τ:延遲時間。

3.2 再熱汽溫對象辨識

以300mw 機組鍋爐為例，通過模型對再熱蒸汽溫度對象進行辨識。選取二階慣性加純遲延環節，粒子維數：[kτt1 t2]

傳函為：

利用粒子群算法對模型進行辨識，

（1）選取適應度函數為：

（2）確定各參數范圍：k?[0.1 10],τ?[50 300],t1=t2?[50 100]。

（3）種群m=40,c1=c2=1.4962

（4）尋優50 代得到最優解，結果為：

最優個體適應值如圖4 所示，優化曲線如圖5 所示，再熱蒸汽溫度控制系統模型辨識結果如圖6 所示。

從辨識結果可以看出，粒子群算法可以很有效地對系統模型進行參數辨識，它有操作容易，易理解，速度快并且辨識精度高等優點。

4 總結

以再熱汽溫控制系統為對象，針對傳統辨識方法的不足。提出基于粒子群算法的再熱溫度控制系統進行辨識，將系統辨識問題轉化為優化問題，使用MATLAB 軟件，對系統參數進行優化，最終得到一個優化后的、可用的模型。實驗結果表明，粒子群算法簡單易行，精度較高。