一種慣性測量單元標定補償方法

陳健 楊富鋒 靳展

（南京理工大學發射動力學研究所 江蘇省南京市 210094）

1 引言

因為尺寸小、成本低、精度高、易于集成和可大規模生產等優點，微機電（MEMS）慣性傳感器受到越來越多人們的歡迎，廣泛應用于民用和軍用領域[1-3]。但由于尺寸與成本的因素，大多數MEMS陀螺儀的零偏穩定性都不是很高，有的甚至達到100°/h。此外，大多數MEMS 傳感器的應用場合是低動態的，加速度在應用過程中整體較小，由其帶來的輸出誤差即g 值敏感系數誤差相比零偏穩定性等帶來的輸出誤差可以忽略，在陀螺儀的標定中通常不做考慮[4]。因而，很少有參考文獻關注研究g 值敏感系數的標定和補償。

同時，在傳統的誤差標定補償方面，常采用靜態旋轉多位置方法、動靜結合方法進行標定[5-7]。為了考慮地球角速度對陀螺儀各方向輸出的影響，需要對轉臺進行復雜的尋北操作來消除載體坐標系與東北天坐標系不重合帶來的誤差。常用的尋北裝置為陀螺經緯儀，操作使用復雜，需要操作人員具有嫻熟的操作經驗和較高的專業素質，而且測試前期的準備時間較久，不利于實驗的快速進行。

因此，本文結合以上兩個問題設計了一種考慮g 值敏感系數的無需尋北的標定補償方法，具有良好的參考和研究意義。

2 慣性測量單元誤差模型建立

慣性測量單元傳統的誤差模型，主要基于零偏漂移誤差、標度因數誤差、非正交性誤差、隨機漂移誤差這四項建立[8-10]，誤差模型分別如下所示：

2.1 陀螺儀

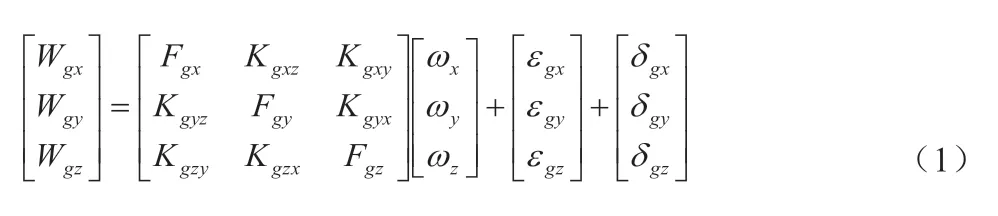
表1：靜態十二位置法標定的陀螺儀與加速度計輸入

表2：陀螺儀各項誤差系數標定結果

表3：加速度計各項誤差系數標定結果

表4：12 個位置的均值與均方差

表4：12 個位置的均值與均方差

是否考慮g 值敏感系數 均值（°/h） 均方差是15.274 0.1465否16.748 1.1863

式（1）中，ωi、Wgi、Fgi、Kgij、εgi、δgi（i=x,y,z j=x,y,z）分 別為陀螺儀的三軸輸入、輸出、標度因數、安裝誤差、零偏與隨機誤差，陀螺儀模型可簡寫為如下形式：其中，Kg、εg、δg為包含陀螺儀各項誤差系數的矩陣，ω、Wg為陀螺儀的輸入輸出矩陣。

2.2 加速度計

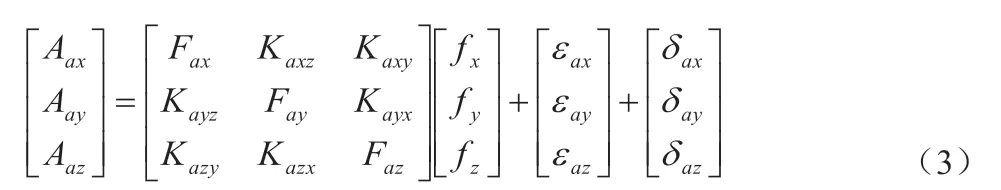
式（3）中，fi、Aai、Fai、Kaij、εai、δai（i=x,y,z j=x,y,z）為加速度計的三軸輸入、輸出、標度因數、安裝誤差、零偏與隨機誤差，加速度計模型可簡寫為如下形式：

其中，Ka、εa、δa為包含加速度計各項誤差系數的矩陣，f、Aa為加速度計的輸入輸出矩陣。

由于隨著科學技術的發展與MEMS 技術的進步，MEMS 傳感器精度不斷提升，陀螺儀的零偏不穩定性等誤差較大的情況逐步改善，g值敏感系數所引起的誤差占比逐步上升，已經不能夠輕易忽略；此外，高精度MEMS 傳感器的應用場合也隨著精度的提升而擴展，高動態的應用場合越來越多。因此，在高性能MEMS 陀螺儀中，也需要對g 值敏感系數進行標定和補償，以提高陀螺儀的測量精度和動態性能。

結合以上問題與情況的考慮，考慮g 值敏感系數建立陀螺儀新的誤差模型。

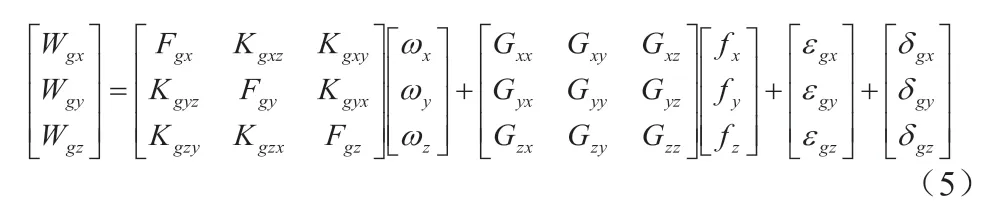
式（5）中，Gij(i=x,y,z,j=x,y,z)為MEMS 陀螺儀的三軸g 值敏感系數，其余參數同式（1）所示。

簡化形式為：

3 IMU標定方案確定

傳統標定方法需要感應地球自轉角速度在東北天三軸分量作為標定依據，因此需要在標定前對轉臺進行尋北，以使載體坐標系與東北天坐標系重合。本文設計了一種考慮g 值敏感系數的無需尋北12 位置標定補償方法，具體步驟如下：

3.1 STIM300的轉臺靜態輸出數據采集與處理

將STIM300 固定安裝在三軸轉臺內框中，X 軸指向天向，旋轉內框調整IMU 初始位置使其Y 軸與中框法線重合，這樣中框旋轉不會帶來天向的誤差，此時內外框法線重合。由于未進行尋北操作，初始位置IMU 的Z 軸只是大致為北，即內外框的初始法線與真北方向存在一個未知的小誤差角α，選取十二位置法進行標定，每個位置以及陀螺和加速度計的輸入值如表1 所示。

操控轉臺將其旋轉到表1 所示的12 個位置，每個位置都靜止采集半小時數據，對每一個位置處采集的數據進行均值化處理，消除隨機噪聲帶來的隨機誤差的影響。經過均值化處理后，得到12個位置的MEMS 陀螺儀與加速度計輸出為：

3.2 陀螺儀和加速度計的零偏計算

考察表1 中12 個位置的陀螺儀與加速度計輸入，易見各方向其和可以正負抵消，因此將這些位置的輸出進行疊加求和計算后，地球自轉角速率和重力加速度項可以消去，得出陀螺儀和加速度計的零偏誤差如下：

其中，εgx、εgy、εgz、εax、εay、εaz為陀螺儀與加速度計的三軸零偏誤差；Wigx、Wigy、Wigz、Aiax、Aiay、Aiaz為陀螺儀與加速度計在12 個位置的X、Y、Z 軸輸出的均值。

3.3 STIM300的轉臺動態速率實驗數據采集

控制轉臺轉動，依次將IMU 的X 軸、Y 軸、Z 軸指向天向，使慣性測量單元轉臺繞X 軸、Y 軸、Z 軸旋轉，通過轉臺速率控制依次輸入各檔速度：±100°/s、±200°/s、±300°/s。每次速率實驗采集10 分鐘的微慣性測量單元輸出數據。

當采集完每個軸的6 次速率實驗的MEMS 陀螺儀輸出數據后，進行均值化處理消除隨機噪聲帶來的隨機誤差的影響。同時利用整圈標定法可以減少地球自轉角速率對陀螺儀輸出的影響，使其水平軸的分量在轉臺旋轉整周時被平均掉。經過整周均值化處理后，得到18 次速率實驗的MEMS 陀螺儀三軸輸出為：

圖1：STIM300 示意圖

圖2：三軸多功能測試轉臺

其中，i=X±、Y±、Z±表示試驗中轉臺繞x，y，z 軸旋轉，+/-表示轉臺正轉或反轉，j 表示轉臺轉速為100°/s、200°/s、300°/s時的實驗數據。

3.4 MEMS加速度計的標度因數與安裝誤差計算

由加速度計的誤差模型式（3）及其簡化形式（4）可知，標度因數與安裝誤差的值均可由矩陣Ka得到，所以只要求得矩陣Ka的值，就能計算出標度因數與安裝誤差的值。由于隨機誤差由數據的均值化處理基本消去，從而可以列出12 個位置加速度計輸出與輸入的關系。

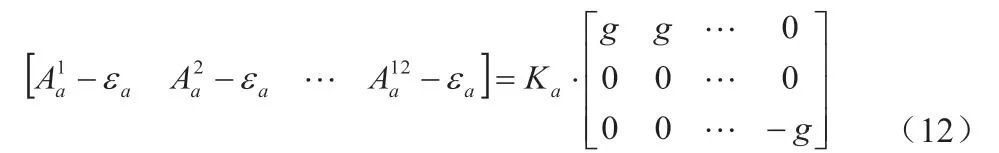
式（12）可簡化為：

其中，加速度計零偏由式（10）已計算出，則A，B 均為已知數，Ka可通過線性最小二乘法求得：

由Ka可得加速度計的標度因數與安裝誤差值。

3.5 陀螺儀的標度因數與安裝誤差計算

同上可知，陀螺儀的標度因數與安裝誤差計算可轉化為Kg矩陣的求解。考察速率實驗陀螺儀與加速度計輸入，由于正反轉只有旋轉軸的陀螺儀輸入不同，兩者取差后可消去零偏與g 值敏感度的影響，以繞X 軸旋轉的一組正反轉數據為例：

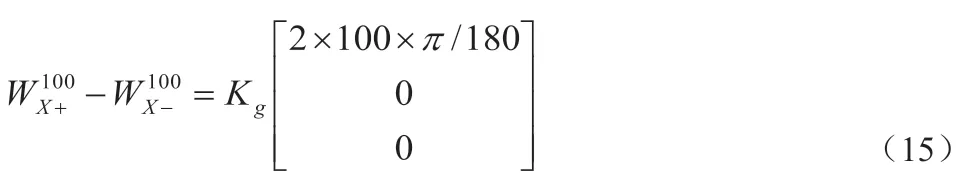
結合速率實驗的所有數據可以列出陀螺儀輸出與輸入的關系：

式（16）可簡化為：

其中，A，B 均為已知數，Kg可通過線性最小二乘法求得：

由Kg可得陀螺儀的標度因數與安裝誤差值。

3.6 陀螺儀的g值敏感度計算

陀螺儀的g 值敏感度計算也可轉化為G 矩陣的求解。考察靜態標定中12 個位置的陀螺儀與加速度計輸入，易見1 與2，3 與4，5 與6，7 與8，9 與10，11 與12 位置的陀螺儀輸入可通過兩兩相加消除北向誤差角α 的影響，以位置1 與2 的數據為例：

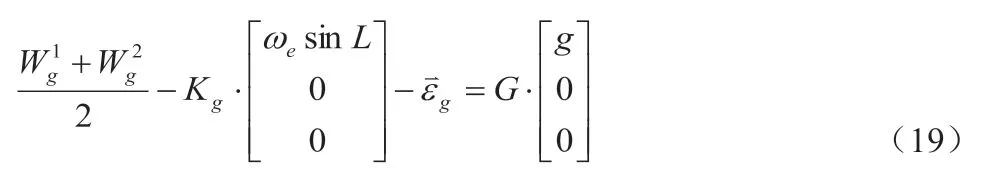
結合靜態12 位置標定的所有數據可以列出陀螺儀輸出與輸入的關系：

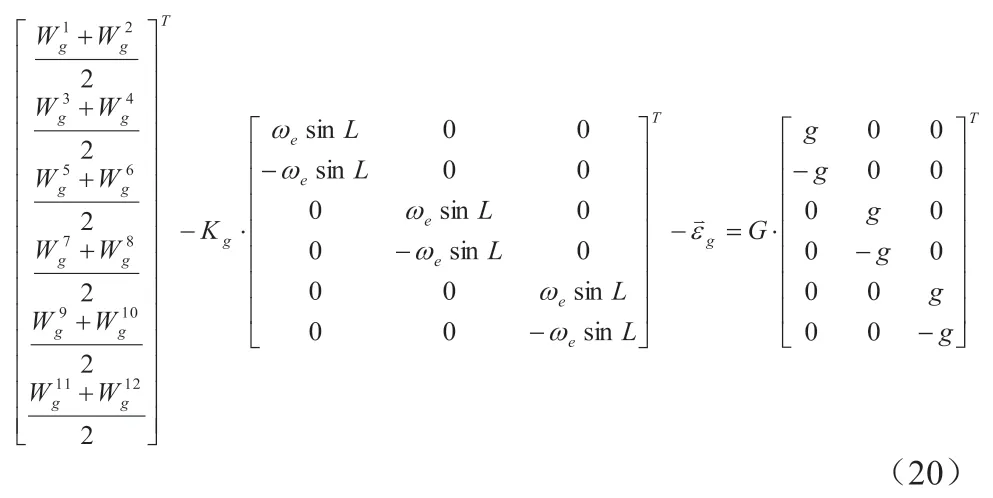
式子可簡化為：

其中，A，B，Kg，εg均為已知數，G 可通過線性最小二乘法求得：

由G 可得陀螺儀的標度因數與安裝誤差值。

綜上，即可計算出陀螺儀與加速度計的各確定性誤差參數值，通過下式對陀螺儀和加速度計輸出進行補償，其中 和 為補償了確定性誤差后的陀螺儀與加速度計輸出。

4 實驗與結果分析

本文使用的STIM300 是一款小型、無GPS 輔助的IMU，內置3 個傾角儀以確保精準的系統調平，對磁場不敏感且進行了全溫補償，所有的軸都相對封裝基準面進行了機械和電氣對準，適合各種商用、軍用制導及慣性導航應用。其示意圖與標定所使用的三軸轉臺如圖1 和圖2 所示。

首先利用傳統的靜態24 位置試驗與速率試驗結合的標定方法對該IMU 系統進行標定。然后，采用本文提出的不尋北12 位置標定方法對該IMU 進行標定，試驗結果如表2 和表3 所示。

從上述標定結果可以看出，不尋北12 位置標定方法精確地標定出了陀螺儀與加速度計的，在不需要尋北的情況下，該方法的標定精度與傳統標定方法的標定精度相當。

接著，為了考察求得的g 值敏感度補償結果的作用，分別對靜態12 位置的陀螺儀輸出進行包含g 值敏感度的補償以及傳統方法的補償。考察表2.1 中各位置的陀螺儀輸入，由于靜態時IMU 只受地球自轉角速度與重力加速度影響，易見：

由于地球自轉角速率的模值ωe=15°?h，易見考慮g 值敏感系數的結果與真實值更為接近。

5 結論

本文提出的標定方法與傳統方法相比具有無需尋北，方便快捷的特點，且考慮了g 值敏感誤差的影響，對于像文中這種高精度IMU 來說，有效地減少MEMS 陀螺儀因加速度所引起的g 值敏感誤差，提高了陀螺儀的動態性能和測量精度，具有重要的工程應用價值。