基于星載GPS 數據的Jason-3 衛星簡化動力學和運動學法精密定軌

郭恒洋，郭金運，楊洲銘，齊林虎，趙春梅

(1.山東科技大學 測繪與空間信息學院，山東 青島 266590；2.中國測繪科學研究院 北京房山人衛激光國家野外科學觀測研究站，北京 100036)

0 引 言

Jason-3 衛星是由美國國家海洋和大氣管理局(NOAA)、歐洲氣象衛星開發組織(EUMETSAT)、法國空間研究中心(CNES)等組織合作開發的測高衛星，于2016 年1 月17 日發射.作為OSTM/Jason-2 衛星的繼任衛星，Jason-3 衛星需要繼續承擔TOPEX/Poseidon、Jason-1 和OSTM/Jason-2 衛星的任務，為全球氣候預測和海洋地形研究提供高精度的監測數據.對于測高衛星，高精度的衛星軌道可以保障衛星測高數據的高精度處理，因此對于Jason-3 衛星的精密定軌至關重要，其軌道徑向精度要求達到厘米級[1].

隨著星載GPS 接收機的發展和應用，星載GPS技術日益成熟，并且星載GPS 觀測數據多，數據精度高，因此星載GPS 定軌技術逐漸成為低軌衛星精密軌道確定的重要手段[2].目前，星載GPS 定軌技術已成功應用于TOPEX/Poseidon、Jason-1、OSTM/Jason-2和HY-2A 等多顆測高衛星以及CHAMP、GRACE 和SWARM 等多顆重力衛星.根據是否使用動力學信息，LEO 衛星定軌方法可以分為運動學(Kinematic)法、動力學(Dynamic)法和簡化動力學(Reduced-dynamic)法.

動力學法定軌的原理是通過精確解算帶有各種力學模型的動力學方程，根據最小二乘法得到顧及各個歷元觀測值的軌道參數，積分得到衛星位置.該方法能以較少的GPS 觀測數據得到可靠的衛星軌道，但是涉及到的力學模型較多，動力學方程復雜.目前關于動力學定軌的研究較少，郭金運[3]等利用星載GPS 雙差數據對CHAMP 衛星進行動力學定軌，定軌精度達到亞分米級；張德成等[4]利用星載GPS 數據，采用非差動力學法定軌，獲得GRACE 衛星的精密軌道，定軌精度達到cm 級.

簡化動力學法定軌的過程與動力學定軌相似，但與動力學定軌的差異在于其使用的力學模型比動力學定軌少.Yunck T 等[5]最早提出了簡化動力學方法，基于星載GPS 觀測數據對TOPEX/Poseidon 衛星進行簡化動力學定軌，定軌的精度優于3 cm；隨后J?ggi等[6]研究了將偽隨機脈沖參數運用到定軌中，成功解算CHAMP 衛星的簡化動力學軌道；Haines 等[7]考慮到相位中心變化(PCV)，解算得到的Jason-1 衛星軌道徑向精度達到1 cm；秦建[8]等利用星載GPS 數據，基于簡化動力學方法得到GRACE 衛星軌道，軌道精度達到cm 級；秦建[9]等利用BERNESE5.0 軟件基于星載GPS 觀測數據對Jason-2 衛星進行非差數據簡化動力學定軌，軌道徑向精度優于6 cm；張德志等[10]利用BERNESE5.2 軟件對Jason-3 衛星進行簡化動力學定軌，軌道徑向精度優于2.2 cm；楊洲銘[11]等使用星載GPS 觀測數據，對GRACE-FO 衛星進行簡化動力學定軌研究，軌道徑向精度優于2 cm；Yang[12]等提出一種監測和修復星載GPS 接收機周跳的方法EEM，成功將該方法應用到SWARM-A衛星簡化動力學定軌中；Qi 等[13]通過添加高階電離層延遲的改進順序，可以提高GRACE-FO 的簡化動力學軌道精度.

運動學法定軌的本質是衛星空間后方交會，根據GPS 衛星精密星歷得到GPS 衛星的位置，再結合低軌衛星的星載GPS 觀測數據，解算出每個歷元下低軌衛星的位置.運動學方法不受力學模型的影響，解算簡單，但是數據缺失或數據觀測質量下降會影響定軌的結果.鄭作亞[14]提出基于歷元間加權的偽距和相位觀測值聯合定軌的方法，實現CHAMP 衛星的運動學定軌，內符合精度達到10 cm；張守建等[15]解算得到的GRACE 衛星運動學軌道精度優于4 cm；張兵兵等[16]利用星載GPS 觀測數據實現了SWARM系列衛星的運動學定軌，軌道徑向精度達到1～2 cm.

對比研究運動學定軌和簡化動力學定軌，可以更加直觀的反映兩種定軌方法的特點.Guo[17]等利用BERNESE5.0 軟件進行HY-2 星載GPS 數據模擬并對HY-2 衛星進行定軌，定軌精度達到cm 級；夏要偉等[18]使用星載GPS 觀測數據，基于運動學和簡化動力學定軌方法，計算SWARM 衛星軌道，定軌精度達到cm 級.

本文基于Jason-3 衛星星載GPS 雙頻觀測數據，實現Jason-3 衛星的簡化動力學法和運動學法精密定軌.主要使用運動學和簡化動力學方法解算精密軌道，通過設置偽隨機脈沖參數吸收大氣阻力和太陽光壓，成功解算出Jason-3 衛星的簡化動力學軌道.同時，不考慮力學模型，成功解算出運動學軌道.為了評價定軌結構，通過載波相位殘差分析、重疊軌道對比、與參考軌道對比、衛星激光測距(SLR)軌道檢核四種方法評價軌道精度.

1 定軌方法及策略

1.1 觀測方程

對于低軌衛星，星載GPS 的雙頻無電離層載波相位觀測方程[19]為

1.2 動力學法

低軌衛星在飛行過程中，會受到多種力的作用，包括地球引力、日月引力、地球非球形攝動、潮汐攝動、大氣阻力、太陽輻射壓、地球輻射壓以及相對論效應等影響[21]，其運動微分方程[22]為

根據測碼偽距可得到先驗軌道r0(t)，動力學法定軌可以看作是一個逐漸改善軌道的過程.其本質是根據最小二乘的方法得到顧及各個歷元觀測值的軌道參數.假設有n個歷元的觀測值，初始歷元的軌道參數為p0，利用數值積分得到 (ti,t0) 時段的狀態轉移矩陣 Φ (ti,t0)，pi=Φ(ti,t0)p0，可建立觀測方程[22]

式(5)也可以寫成V=BΦP0?L，其中，V為觀測數據殘差向量矩陣，B表示由觀測數據構建的誤差方程的系數矩陣，L表示常數項矩陣.

1.3 簡化動力學

由于低軌衛星所在的空間環境復雜，動力學模型難以對大氣阻力和太陽光壓進行模式化處理，因此動力學定軌精度不可避免的受到未被模式化的攝動因素的影響.

在衛星定軌過程中，每隔一段時間，在特定的歷元上對衛星徑向(R)、切向(T)和法向(N)設置一組瞬時變化值，該值稱為偽隨機脈沖.在簡化動力學求解衛星軌道的過程中引入偽隨機脈沖參數，每周期估計一次脈沖作為制約因子，以改善太陽光壓誤差[23].

簡化動力學方法計算衛星軌道與動力學法類似，都是采用力學模型與數值積分求解衛星軌道，但差異在于簡化動力學方法所使用的力學模型比動力學方法少，簡化動力學方法通過附加偽隨機參數，平衡了動力學與運動學兩方法，通過不斷迭代求解改善軌道質量，使得定軌結果更加準確.

1.4 運動學法

運動學法是指利用星載GPS 觀測數據和地面站的跟蹤數據，根據空間距離后方交會的原理，解算衛星軌道的方法.運動學法定軌的優點是解算過程簡單，不受低軌衛星動力學模型的影響，但是解算出的軌道是離散的點位，需要擬合后得到連續軌道[24-25].運動學定軌精度主要受到GPS 數據質量的影響，包括GPS 觀測數據的質量，GPS 衛星數量和空間結構，GPS 衛星軌道和鐘差質量等[26].

在GPS 數據處理過程中，參數數量非常龐大，無法使用常規的最小二乘方法.需要通過最小二乘方法中的參數消元法分類處理不同的參數，以提高解算效率.在動態定位中，測站位置和接收機鐘差參數與時間相關，而對于整周模糊度參數，若不發生周跳，可以將整周模糊度參數當作常數.因此，先將這些與時間相關的參數從法方程中消去，只解算與歷元變化無關的參數；得到這些與歷元變化無關的參數后帶回到初始方程，再逐歷元解算提前消掉與時間有關的參數.

對式(1)進行線性化后，歷元i的誤差方程為

式中：Vi為歷元i線性化觀測值殘差向量；xi表示與歷元i相關的參數(測站坐標、接收機鐘差)改正量；y表示在此觀測時間內的整周模糊度參數改正量；Ai和Bi分別為相應參數的系數矩陣；Li為歷元i的線性化常數陣；pi為歷元i的權矩陣.

式(6)的法方程為

考慮第1 個歷元的向量y的先驗信息，則第2 個歷元的法方程為

再從上式消去隨歷元變化的參數x2，則

聯合式(9)得

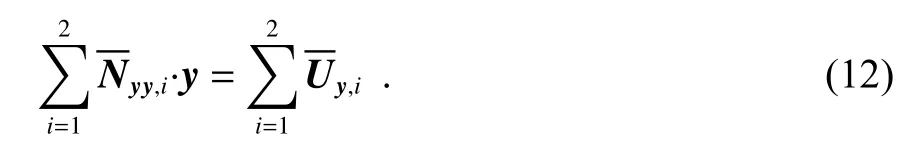
以此類推，則在第n個歷元消去隨歷元變化的參數xn，相應的向量y的法方程為

1.5 定軌策略

本文基于Jason-3 衛星2019-01-25—01-31 年積日DOY 25—31 共7 天的星載GPS 觀測數據，進行精密定軌研究.主要采用簡化動力學法和運動學法，利用Jason-3 衛星7 天星載GPS 數據解算衛星的精密軌道，定軌弧段為24 h.通過載波相位殘差分析、重疊軌道對比、與參考軌道對比以及SLR 軌道檢核四種方法對比，分析Jason-3 衛星簡化動力學定軌和運動學定軌的精度.簡化動力學定軌的策略如表1 所示.

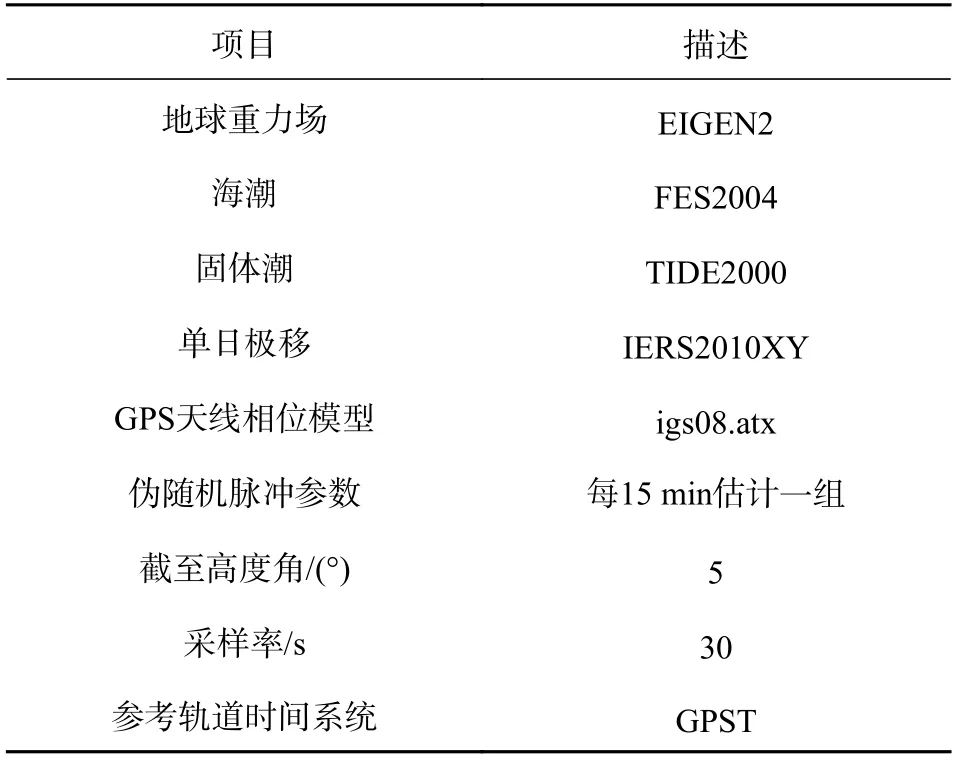
表1 Jason-3 衛星簡化動力學定軌策略

本文利用Bernese5.2 軟件對Jason-3 衛星定軌進行研究，簡化動力學和運動學定軌的技術路線[18]如圖1 所示.

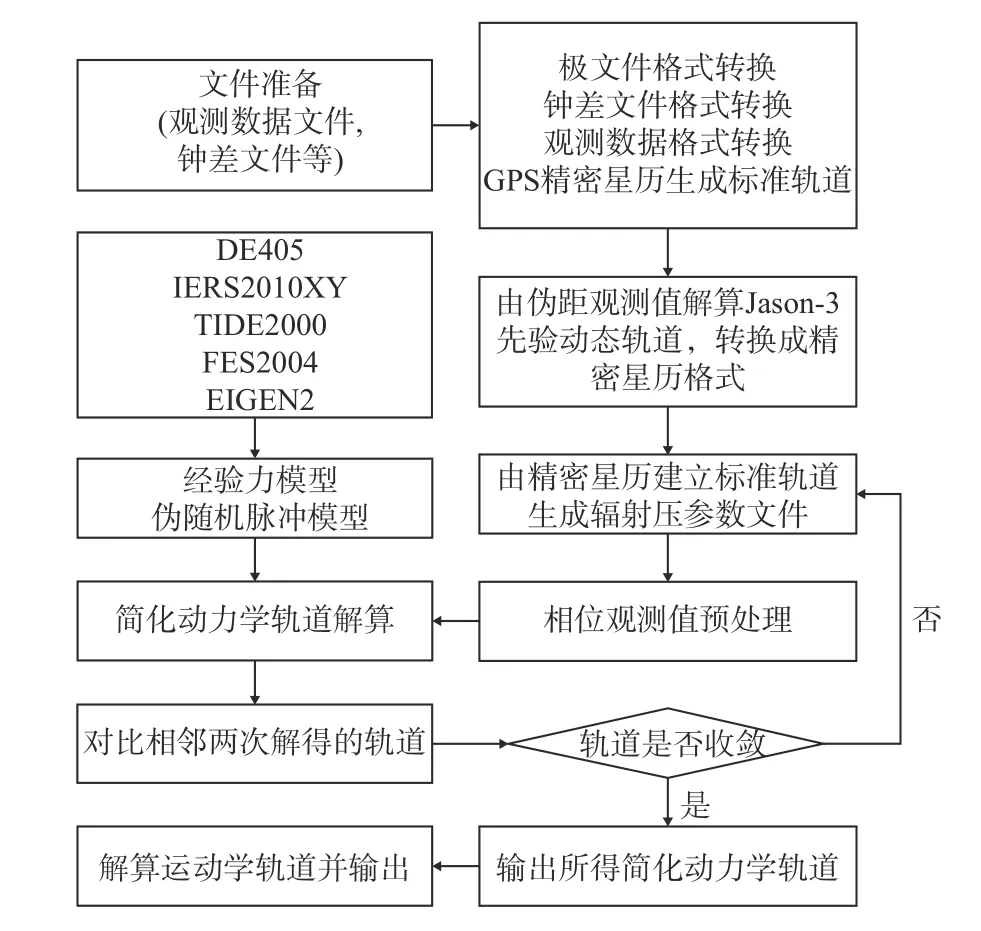
圖1 Jason-3 衛星定軌技術路線

由于GPS 觀測的是從GPS 衛星發射天線的相位中心到LEO 衛星天線相位中心間的距離，而GPS精密星歷提供的是衛星質心的坐標，因此需要進行衛星天線相位中心改正.天線相位中心的誤差通常分為兩部分：天線相位中心偏差(PCO)和天線PCV；PCO 指天線瞬時相位中心的平均值與天線參考點之間的距離，PCV 指天線瞬時相位中心的平均值與天線瞬時相位中心的距離[27-28].

在與參考軌道對比時，需要考慮將簡化動力學軌道和運動學軌道與參考軌道在時間系統上進行統一.由于國際DORIS 服務(IDS)官方網站(https://idsdoris.org)提供的Jason-3 衛星參考軌道的時間系統是國際原子時(TAI)，而簡化動力學軌道和運動學軌道的時間系統是GPS 時(GPST)，TAI 與GPST 存在19 s 的偏差，即TAI?GPST=19 s，所以需要事先對IDS提供的參考軌道做預處理，將參考軌道的時間系統轉換為GPST，以方便與參考軌道對比.

2 數據來源

本文定軌采用CNES(ftp://ftp-access.aviso.altimetry.fr)提供星載GPS 雙頻觀測數據，采樣間隔為10 s，觀測弧段為2019-01-25—01-31 年積日DOY 25—31共7 天的觀察數據；采用歐洲定軌中心(CODE)(ftp://ftp.aiub.unibe.ch/CODE)提供的GPS 衛星精密星歷采樣間隔為30 s 的衛星鐘差產品、地球自轉參數數據；采用IDS 官方網站(https://ids-doris.org)提供的Jason-3 衛星精密軌道作為參考軌道，它是法國CNES 利用DORIS 和GPS 觀測數據聯合定軌解算得到的，軌道的徑向精度優于1.5 cm[1,27]；采用NASA 官方網站(https://cddis.nasa.gov/archive/slr)提供的SLR軌道檢核觀測數據，其定軌精度可以達到1～2 cm.相關數據的詳細信息如表2 所示.

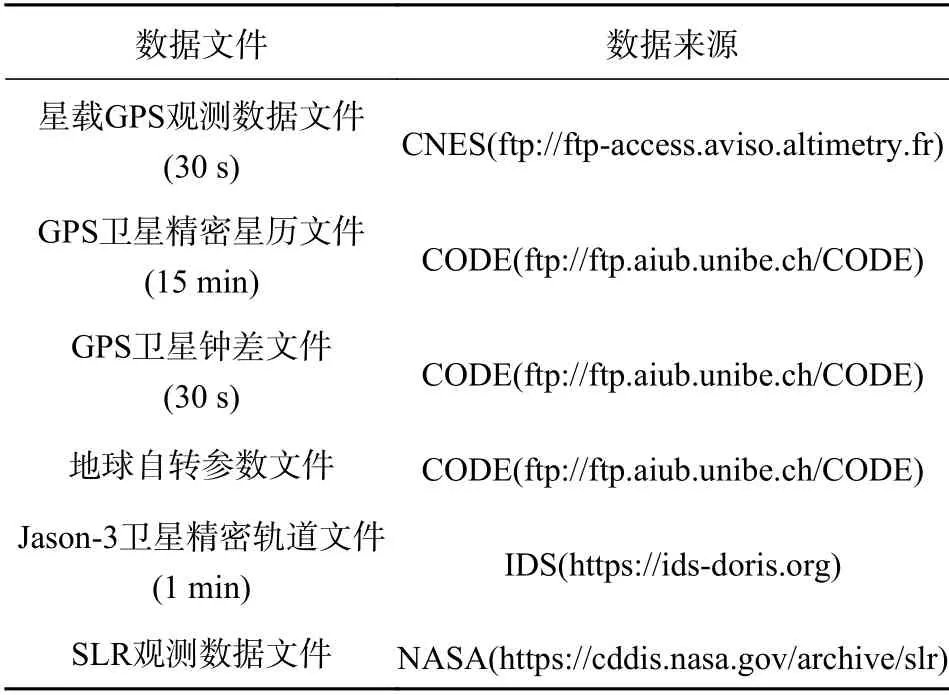
表2 數據來源

3 Jason-3 衛星定軌結果與對比分析

本文對于Jason-3 衛星簡化動力學軌道和運動學軌道的精度檢核分為內符合精度檢核和外符合精度檢核兩個部分.內符合精度檢核采用載波相位殘差分析和重疊軌道對比兩種方法，外符合精度檢核采用與參考軌道對比和SLR 軌道檢核兩種方式.

3.1 載波相位殘差分析

評價軌道的精度，首先要看觀測數據的擬合程度.對于簡化動力學定軌而言，載波相位殘差主要指模型化的誤差和未被模型化的誤差，因此殘差均方根(RMS)值可以作為內符合精度評定的指標之一[29].殘差RMS 值越小，說明內符合精度越高

本文采用雙頻數據消電離層(LC)組合對星載GPS 觀測數據進行處理，消除電離層延遲一階主項的影響[30].圖2 為2019-01-25—01-31 年積日DOY 25—31 共7 天中每天的簡化動力學定軌和運動學定軌兩種方法定軌總的相位殘差RMS 值.結果如表3 所示.

圖2 載波相位殘差RMS

表3 載波相位殘差RMS 值匯總統計 mm

對于簡化動力學方法定軌，結合圖2 所示的每天的殘差RMS 值和表3 統計的總殘差RMS 值，可以發現7 天內的殘差RMS 值相當接近，均在7～8 mm，這說明Jason-3 衛星搭載的GPS 接收機獲取的數據穩定，簡化動力學定軌的策略得當，結果可靠.

類似地，對于運動學方法定軌，結合圖2 所示的每天的殘差RMS 值和表3 統計的總殘差RMS值，可以發現7 天內的殘差RMS 值相當接近，均在5.0～5.5 mm，這說明運動學定軌沒有受到力學模型等模型誤差的影響，運動學定軌結果可靠.

3.2 重疊軌道對比

本文使用2019-01-25—01-31 年積日 DOY 25—31 共7 天的Jason-3 衛星星載GPS 觀測數據進行簡化動力學定軌和運動學定軌，對軌道結果按照重疊時段進行對比以驗證其精度.將單天的定軌分為2 個弧段進行，第一個弧段為0～18 h，第二個弧段為12～24 h，兩個弧段的重疊時間為6 h.重疊時段的軌道通過兩次相互獨立的定軌得到，可以通過對比重疊時段的兩段軌道，來檢核定軌結果的內符合精度，結果如圖3所示.匯總統計結果如表4 所示.

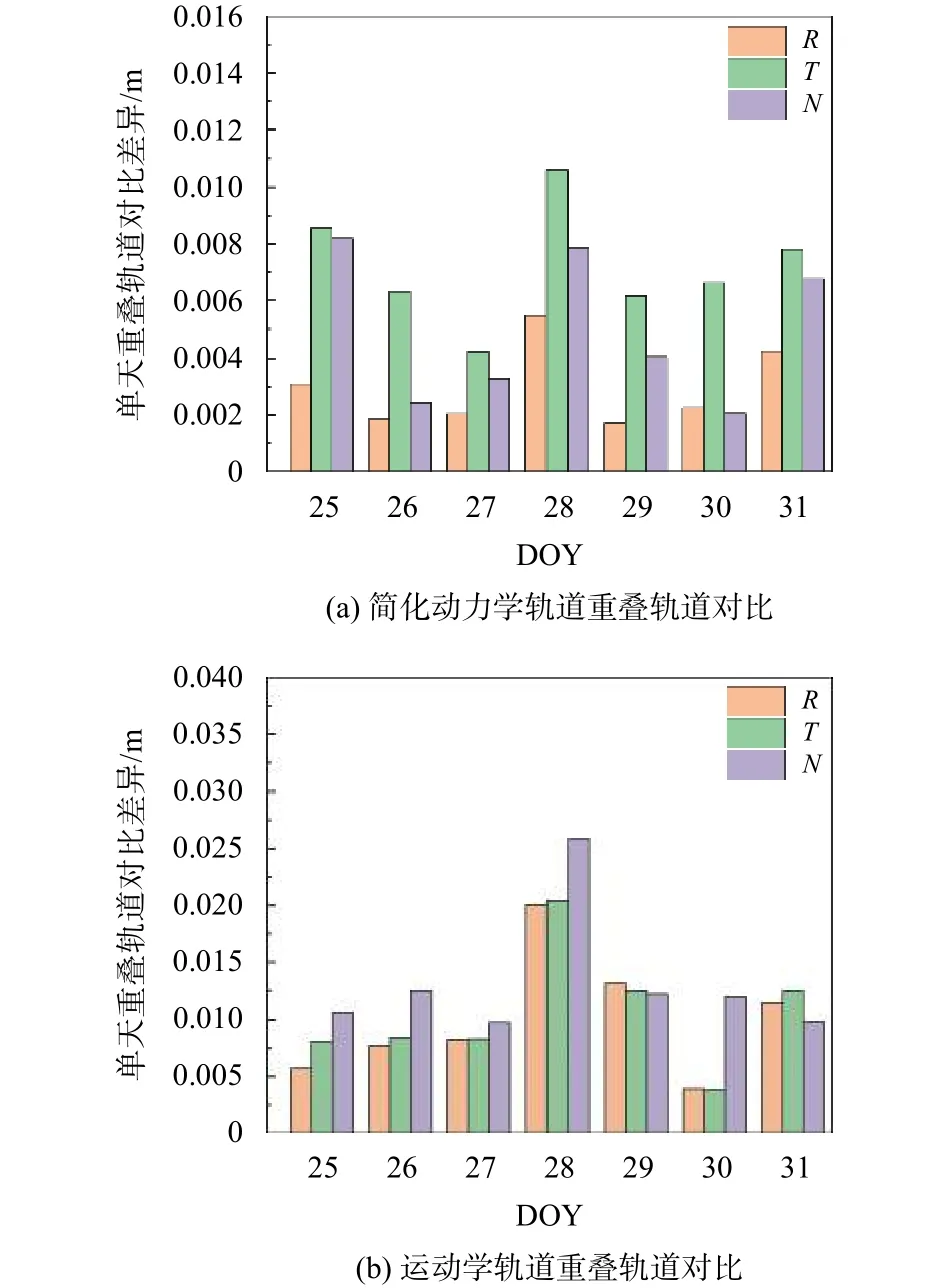
圖3 2019-01-25—01-31 DOY 25—31 重疊軌道對比差異圖

由圖3 所示的單天重疊軌道對比差異圖可以看出，對于簡化動力學軌道，差異在R向上的RMS 值在0.001～0.005 m 波動；在T向上的RMS 值在0.004～0.01 m 波動；在N向上的RMS 值在0.002～0.008 m波動.表4所示的簡化動力學軌道重疊時段對比7 天匯總的結果是，重疊軌道的差異在R向上的RMS 值為0.32 cm；在T向上的RMS 值為0.97 cm；在N向上的RMS 值為0.55 cm.

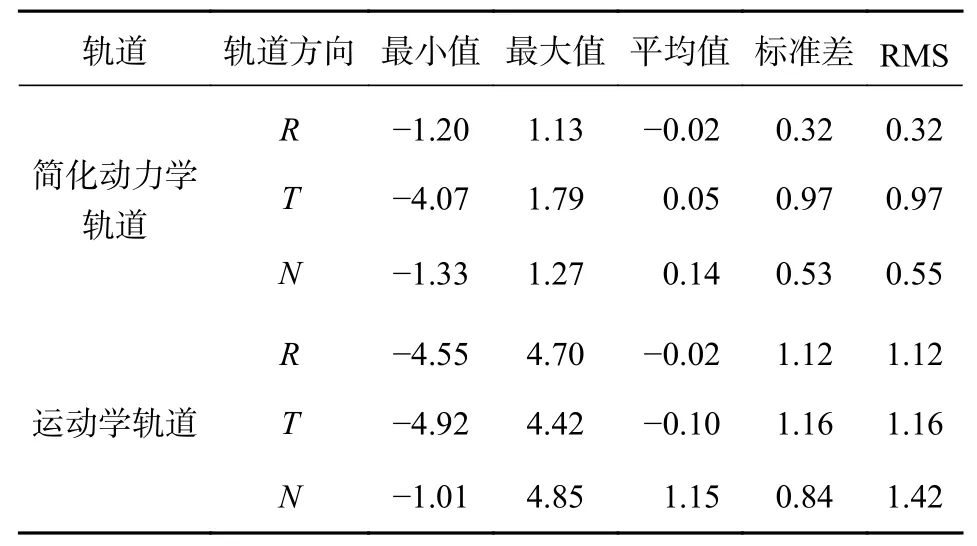
表4 重疊軌道對比殘差7 天匯總統計結果 cm

類似的，對于運動學軌道，由圖3 可以看出，差異在R向上的RMS 值在0.003～0.013 m 波動；在T向上的RMS 值在0.003～0.012 m 波動；在N向上的RMS 值在0.009～0.025 m 波動.表4 所示的運動學軌道重疊時段對比7 天匯總的結果是，重疊軌道的差異在R向上的RMS 值為1.12 cm；在T向上的RMS值為1.16 cm；在N向上的RMS 值為1.42 cm.

對Jason-3 衛星進行的簡化動力學軌道和運動學軌道進行重疊軌道對比，簡化動力學軌道的重疊軌道對比整體差異的RMS 值在R、T、N三個方向分別為0.32 cm、0.97 cm、0.55 cm，運動學軌道的重疊軌道對比整體差異的RMS 值在R、T、N三個方向分別為1.12 cm、1.16 cm、1.42 cm.統計結果表明，重疊時段軌道的差異較小，定軌內符合精度達到cm 級.

3.3 與參考軌道對比

本文采用IDS 官方網站(https://ids-doris.org)提供的Jason-3 衛星精密軌道作為參考軌道，該軌道是CNES 利用DORIS 和GPS 觀測數據聯合定軌解算得到的，軌道的徑向精度優于1.5 cm[1].以IDS 官方網站提供的精密軌道作為參考軌道，將簡化動力學軌道和運動學軌道分別與之對比，得到軌道殘差的RMS 值對Jason-3 衛星的簡化動力學軌道和運動學軌道進行外符合精度評定與參考軌道對比的單天結果如圖4 所示.將Jason-3 衛星7 天的簡化動力學軌道和運動學軌道分別與參考軌道對比，統計得到的軌道殘差，整體信息如表5 所示.

圖4 簡化動力學軌道和運動學軌道分別與參考軌道對比結果圖

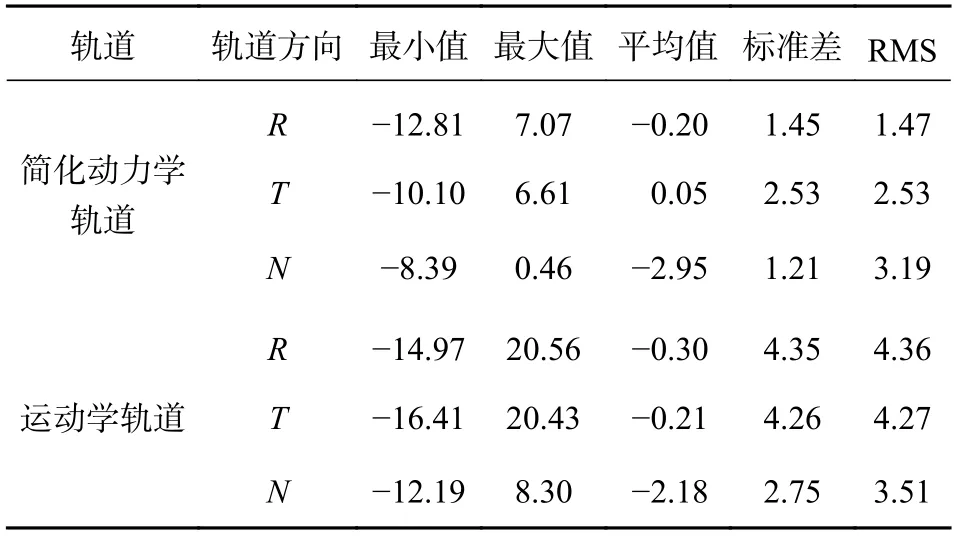
表5 簡化動力學軌道和運動學軌道分別與參考軌道對比7 天匯總結果統計 cm

從圖4(a)可以看出，簡化動力學軌道與參考軌道對比，在R向上的RMS 值在0.012～0.016 m 波動；在T向上的RMS 值在0.019～0.038 m 波動；在N向上的RMS 值在0.029～0.033 m 波動.圖4(a)中可以看出DOY 28 的軌道殘差切向精度最差；而其他6 天的簡化動力學軌道與參考軌道對比結果均是法向精度較差，Jason-3 衛星的簡化動力學軌道徑向精度較高.

從圖4(b)中可以看出，運動學軌道與參考軌道對比得到的軌道殘差，在R向上的RMS 值在0.036～0.046 m 波動；在T向上的RMS 值在0.034～0.047 m波動；在N向上的RMS 值在0.029～0.043 m 波動.圖4(b)中可以看出DOY 28 的軌道殘差切向精度最差；而其他6 天的結果均是徑向精度較差.Jason-3 衛星的運動學軌道，法向精度較高.

從表5 可以看出，簡化動力學軌道與參考軌道對比的殘差在R向上的RMS 值為1.47 cm；在T向上的RMS 值為2.53 cm；在N向上的RMS 值為3.19 cm；整體上看，簡化動力學軌道的徑向精度較高.對于運動學軌道，殘差在R向上差異的RMS 值為4.36 cm；在T向上差異的RMS 值為4.27 cm；在N向上差異的RMS 值為3.51 cm；整體上看，運動學軌道的法向精度較高.分別將Jason-3 衛星的簡化動力學軌道和運動學軌道與參考軌道對比，說明定軌內符合精度達到cm 級.

3.4 SLR 軌道檢核

衛星激光測距技術是衛星精密定軌的一種重要手段，本文選擇由NASA 官方網站(https://cddis.nasa.gov/archive/slr)提供的SLR 觀測數據，其定軌精度可以達到1～2 cm[31].

SLR 軌道檢核是利用軌道提供的衛星坐標和SLR 臺站坐標計算出站星距離，并與對應歷元下SLR臺站的觀測數據對比，從而評定簡化動力學方法和運動學法定軌的精度.

計算Jason-3 衛星與SLR 臺站之間的距離公式為

式 中：(xs,ys,zs) 為衛星的坐標；(xi,yi,zi) 為SLR 臺 站i的坐標.

將站星距歸算到SLR 臺站到衛星質心的距離[32]

由于SLR 軌道檢核數據包含一些誤差，如對流層折射等，因此需要對SLR 軌道檢核觀測數據進行預處理，觀測數據的預處理主要包括對流層折射、廣義相對論、質心補償、測站偏心修正等[33].比較SLR臺站的觀測值與由軌道提供的衛星坐標和SLR 臺站坐標計算的距離值，統計SLR 軌道檢核殘差的RMS值，將單天的RMS 值繪制成如圖5 所示的柱狀圖.

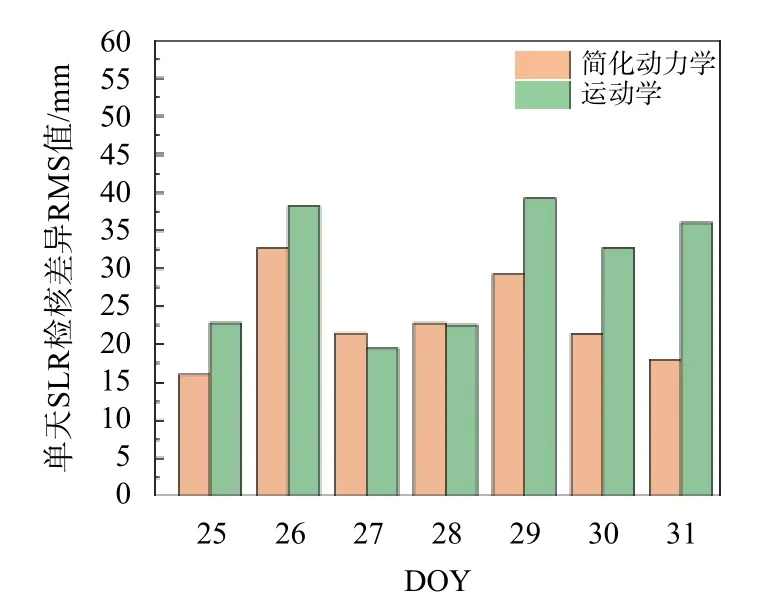
圖5 單天SLR 軌道檢核殘差RMS 值

如圖5 所示，可知簡化動力學軌道的SLR 軌道檢核殘差RMS 值在15～32 mm，而運動學軌道的SLR 軌道檢核殘差RMS 值在19～39 mm.

如表6 所示，Jason-3 衛星共有7 個測站901 個NP(Normal Point)數據，分別匯總統計SLR 軌道檢核的殘差，簡化動力學軌道的SLR 軌道檢核殘差RMS值為2.41 cm，運動學軌道的SLR 軌道檢核殘差RMS值為3.28 cm.實驗結果說明簡化動力學軌道精度整體優于2.1 cm，運動學軌道精度整體優于3.3 cm.這說明Jason-3 衛星軌道的外符合精度可達cm 級，定軌精度較高.

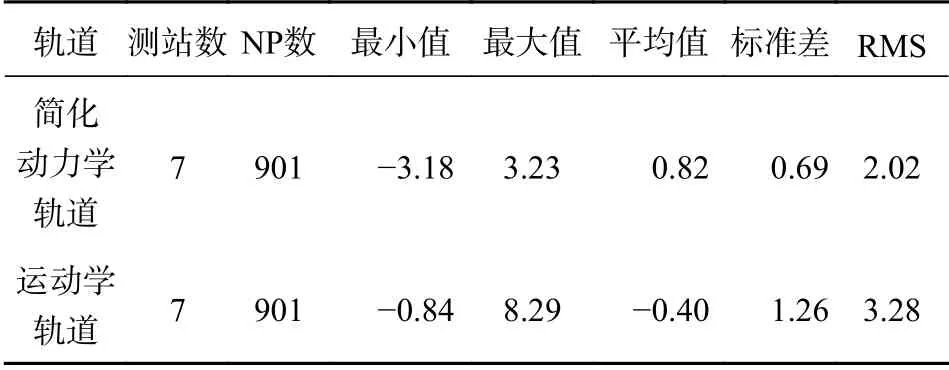
表6 SLR 軌道檢核7 天匯總結果統計 cm

4 結 語

本文利用Jason-3 衛星星載GPS 觀測數據，基于簡化動力學方法和運動學方法解算Jason-3 衛星的軌道，并通過載波相位殘差分析、重疊軌道對比、參考軌道對比和SLR 軌道檢核進行精度評定，得到如下結論：

1)通過相位殘差RMS 值可以看出，簡化動力學軌道的相位殘差RMS 在0.7～0.8 cm，運動學軌道的相位殘差RMS 在0.50～0.55 cm.這說明Jason-3 衛星定軌策略可靠，在解算軌道過程中誤差項消除較為理想，定軌結果較為穩定.

2)分別將Jason-3 衛星兩個時段的簡化動力學軌道和運動學軌道重疊對比，得到7 天的重疊軌道對比匯總的結果.簡化動力學軌道重疊時段R向上差異的RMS 值為0.32 cm，T向上差異的RMS 值為0.97 cm，N向上差異的RMS 值為0.55 cm；運動學軌道重疊時段R向上差異的RMS 值為1.12 cm，T向上差異的RMS值為1.16 cm，N向上差異的RMS 值為1.42 cm.這說明簡化動力學定軌和運動學定軌的內符合精度均達到cm 級.

3)分別將Jason-3 衛星的簡化動力學軌道和運動學軌道與IDS 官網提供的精密軌道對比，得到7 天匯總的結果.簡化動力學軌道與參考軌道對比得到的殘差在R向上的RMS 值為1.47 cm，在T向上的RMS 值為2.53 cm，在N向上的RMS 值為3.19 cm；運動學軌道與參考軌道對比得到的殘差在R向上的RMS 值為4.36 cm，在T向上的RMS 值為4.27 cm，在N向上的RMS 值為3.51 cm.這說明簡化動力學軌道和運動學軌道的外符合精度均達到cm 級.

4)利用NASA 提供的SLR 軌道檢核觀測數據對Jason-3 衛星的簡化動力學軌道和運動學軌道精度進行檢驗，證明簡化動力學軌道精度整體優于2.1 cm，運動學軌道精度整體優于3.3 cm.這說明Jason-3 衛星的軌道外符合精度達到cm 級.

從本文實驗結果來看，Jason-3 衛星的簡化動力學軌道和運動學軌道均達到cm 級的精度.