聯合高度角與信噪比的精化隨機模型及其對高緯度精密單點定位的影響

呂明慧，李薇，張寶成，柴艷菊

(1.中國科學院精密測量科學與技術創新研究院，武漢 430071；2.中國科學院大學，北京 100049)

0 引 言

精密單點定位(PPP)是指利用接收機獲取衛星到地面觀測點的偽距和載波相位信息，結合事后高精度的軌道和鐘差產品，利用函數模型和其他誤差改正模型來削弱衛星端、接收機端以及傳播路徑上的誤差影響，實現高精度定位定軌的方法[1-3].

全球衛星導航系統(GNSS)單點定位模型包括函數模型和隨機模型.函數模型保證了定位過程中各數據參量之間相互關系的準確性，隨機模型則描述了觀測量的先驗統計特性.現有的隨機模型有等權模型、高度角模型以及信噪比(SNR)模型等，很多學者針對這幾種模型的適用條件以及各模型之間的精度比較做了細致地研究[4-5].針對PPP 中不同觀測條件等因素的影響，現已存在一些相應的研究，以上述傳統隨機模型為基礎發展了新的方法.王郁茗等[6]針對海面GNSS 觀測中多路徑誤差對定位精度存在嚴重影響的情況，將海面反射對衛星信號傳播路徑的影響考慮進去，結合高度角模型提出了一種自適應選權隨機模型.潘宇明等[7]認為觀測值的噪聲無法準確地用一個特定的經驗模型來描述，因此利用濾波中的寬窄巷組合觀測值實時地估計衛星觀測值的噪聲，從而得到自適應偽距-相位比隨機模型.對流層殘余延遲在PPP 解算過程中為未建模誤差，有學者利用衛星高度角與大氣延遲殘留誤差強相關的特性，提出了一種基于天頂映射函數的隨機模型，用于降低殘余誤差較大的衛星觀測值的權重.利用該模型驗證了低、中、高緯度地區的測站，結果表明天頂映射函數相關的隨機模型在高緯度地區的精度改善效果最好[8].上述大部分研究都是針對某一特殊需求對傳統隨機模型做出改進，但以精化隨機模型來整體地提高定位精度尚沒有太多研究.本文利用主成分分析法(PCA)確定高度角和SNR 在GNSS 觀測噪聲中的貢獻建立精化隨機模型，實現了在不增加PPP 基本計算量的同時提高定位精度，并通過實際算例驗證和分析該精化隨機模型在高緯度地區實施PPP 的效果.

1 單點定位模型

1.1 單點定位函數模型

在GNSS 觀測中，函數模型由單點定位的基本原理確定，描述了已知量與未知參數之間的關系，利用衛星位置作為已知點位，通過空間距離后方交會確定地面觀測點的位置.

忽略某些誤差的影響后，某一歷元的基本觀測方程[9]為

各觀測量和已知量之間的函數關系已確定，但該函數模型是在各觀測值同精度的情況下建立的，實際觀測中由于各種因素的影響會使得最小二乘計算結果產生較大偏差，隨機誤差增大，因此針對復雜的觀測環境建立精化隨機模型以提高定位結果的精度是非常有必要的.

1.2 單點定位隨機模型

1.2.1 高度角模型

單點定位中的隨機模型通過某一評價指標描述GNSS 衛星觀測值的統計特性.高度角模型以衛星高度角為變化量反映衛星觀測數據的質量，研究表明：衛星高度角越高，觀測數據的質量越好，定位結果的精度越高[10].但有學者認為高度角模型中包含多路徑誤差，對定位精度產生了不好的影響[6].衛星高度角模型[8,11]一般表示為

式中：σ2為各衛星觀測值的方差；為參考方差；α 為衛星高度角.本文將利用該高度角模型進行精化隨機模型的構建.

范士杰等[12]認為低高度角衛星觀測值中包含了更多的大氣信息，利用這些大氣信息有助于得到更高精度的對流層天頂延遲(ZTD)，從而建立了以余弦函數為基礎的隨機模型

經國內外學者研究證明，該隨機模型的ZTD 與國際GNSS 服務(IGS)產品相差2 mm 左右，優于其他隨機模型[13].低高度角衛星觀測值被賦予較大權重時，多路徑誤差的影響也隨之增大，因此該模型只適用于單獨研究ZTD 誤差.

1.2.2 SNR 模型

GNSS 觀測噪聲對數據質量有很大影響，SNR 是指觀測過程中接收到的有效信息與噪聲信息的比值，SNR 越大說明數據質量越好，因此可以利用SNR 反映觀測數據的質量.Brunner 建立了一種利用SNR 表示載波相位中誤差的隨機模型[14-15]

式中：Ci為一個常數，在利用L1載波的SNR 計算時，取C1=0.002 24 m2Hz，利用L2載波的SNR 進行計算時，取C2=0.000 77 m2Hz.C為載波的能量密度，N0為噪聲的能量密度，C/N0即為SNR.

2 引入PCA 的高度角-SNR 隨機模型

基于對上述隨機模型的研究，僅顧及高度角或SNR 的傳統隨機模型無法滿足現階段高精度定位的需求，且不同的隨機模型對于某些誤差有很好地削弱效果，但總體定位精度仍然有待提高.戴吾蛟等[4]的研究表明：高度角模型在處理對流層殘余誤差方面的效果較好，針對衛星信號傳輸過程中引起的衍射誤差的削弱效果則不如SNR 模型，因為高度角值較大的衛星發生衍射后仍被賦予較高的權重，使得定位結果坐標序列的平滑性不如SNR 模型，因此建立一種綜合考慮對流層殘余誤差、衍射誤差和其他誤差影響的精化隨機模型是非常有必要的.已有研究表明高度角與SNR 之間呈正相關關系[16]，但并不是簡單的線性關系.PCA 主要用于將一組可能存在相關性的變量通過正交變換轉換成一組新的線性不相關的變量，轉換后的變量被稱為主成分[17].接下來將利用PCA對高度角和SNR 進行數學建模，確定它們在精化隨機模型中的信息貢獻率.

2.1 PCA

PCA[18]方法最早是由Fukunaga 給出了詳細介紹，主要思想是利用降維的方法在損失很少原始信息的前提下把多個指標轉化為幾個不相關的綜合指標，即每個主成分都是原始變量的線性組合，且各個主成分之間互不相關，使得主成分比原始變量具有某些更優越的性能.

2.2 高度角-SNR 隨機模型

已有研究表明衛星高度角與SNR 之間存在相關性且并非簡單的線性關系，而衍射誤差和對流層誤差在PPP 的過程中是不可被忽略的，對高度角和SNR進行主成分分析，新的主成分之間并不存在相關性，這一點有利于隨機模型中方差協方差陣的計算，并且所得到的主成分可以基本保留原數據的全部信息，不會出現正交化或降維后的信息損失，因此該方法滿足PPP 對隨機模型的需求.

基于PCA 確定GNSS 觀測噪聲中高度角和SNR的貢獻時，首先要得到新的主成分，從而確定權重，處理策略為：將衛星高度角 α 和SNRS組合成矩陣X，此處的S指GPS 衛星信號中L1載波的SNR 數據，其他載波相應的精化隨機模型可依此類推.指標因子的個數為p，此模型中p=2，分別是高度角和SNR 因子，設第j個指標因子的數據有n個，n為衛星的數量.則矩陣X的表達式為

對矩陣X標準化，將其從一個變量轉化為無量綱的純數字，以便處理量級和單位不同的指標，從而進行主成分分析.若兩種評價指標的數值不在一個數量級上，則標準化步驟必不可少.對數據進行0～1 標準化處理得到：

式中，y1、y2分別為第一主成分和第二主成分.理論上選取能夠將原信息表達出85%的主成分即可，以便于更好地達到降維的目的.對于高度角-SNR 精化模型來說，該模型的原變量只有高度角和SNR，能夠提取出的主成分有兩個，并沒有降維方面的需求，為了能更好地表達隨機模型對觀測數據質量的先驗統計信息，將兩個主成分全部納入到隨機模型中，可得

權重可以看作是原指標在各個主成分中對應的方差貢獻率，因此求得各主成分中不同指標對應線性組合的系數，而后進行歸一化處理即可得到指標權重.

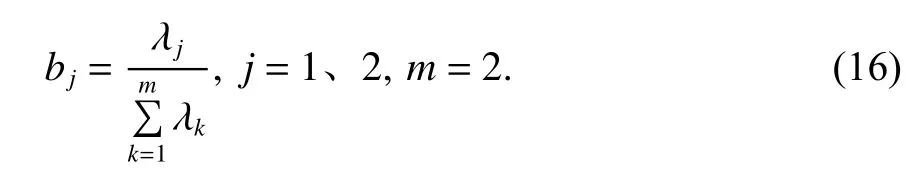
式中，bj為第j主成分的信息貢獻率.主成分表達式由原指標的線性組合形式給出，根據線性組合系數可求得原指標占該主成分的信息貢獻率為

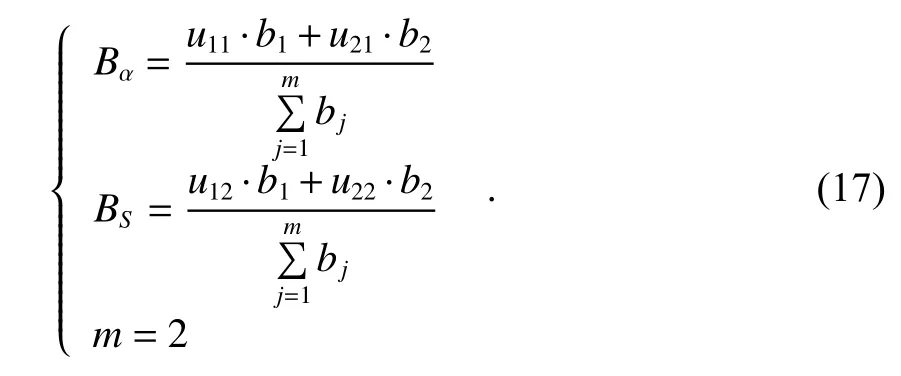
式中，Bα、BS分別為高度角和SNR 在精化隨機模型中的權重.為保證精化隨機模型不受單位的限制，將高度角和SNR 數據進行0～1 標準化，按比例進行縮放使其處在一個特定的區間以去除量綱的限制.設分別為歸一化處理后的高度角與SNR 在GNSS 觀測噪聲中的權重，包含了SNR 和高度角模型0～1 標準化的數學信息.綜合考慮高度角與SNR對GNSS 觀測數據質量的影響所得到的方差為

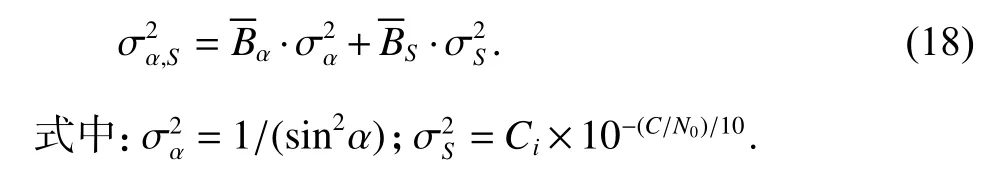
將方差乘以參考方差即為PPP 函數模型的權陣.為方便敘述，下文將此引入PCA 的高度角-SNR 精化隨機模型簡稱為精化隨機模型.

對GNSS 觀測值中高度角和信噪比進行相關性分析得出：其相關性因子為0.9，在統計學中一般認為相關性因子大于0.7 時，數據之間存在相關性，因此高度角與信噪比強相關.利用主成分分析法確定了GNSS 觀測噪聲中高度角與信噪比的貢獻率分別為29.3%和70.7%，可以表達出累計信息量的100%.同時還利用熵權法對數據進行處理，高度角的信息熵為0.98，相應信息效用值為0.020 1；而信噪比的信息熵為0.99，信息效用值為0.008 3，因而熵權法確定高度角與信噪比的權重分別為：70%與30%.經數據驗證發現其精度不及主成分分析法確定的隨機模型高，特別是在高程方向，誤差增加約5%～10%.

3 實驗與分析

在全球范圍內均勻選取2019 年2 月19 日8 個IGS 站實施PPP，比較精化隨機模型和僅顧及高度角或SNR 的傳統隨機模型的三維點位精度，相關解算策略如表1 所示.IGS 測站信息及其解算精度統計結果如表2 所示，可以發現精化隨機模型對于高緯度地區定位精度的改善最為明顯.初步分析由于地理位置的影響，中低緯度地區對流層延遲的未建模誤差較大，高度角模型對于對流層延遲未建模誤差的削弱效果較好，而SNR 模型在解決由于傳輸路徑引起的衍射誤差影響的方面更有優勢.精化隨機模型中高度角的權重要小于SNR，因此對于中低緯度地區的定位精度的改善效果相對較差.從實驗結果來看也驗證了這一設想，在中低緯度地區實施PPP，高度角模型效果好于SNR 模型，且精化隨機模型定位精度較差的測站其ZTD 的精度也比較低.

表1 PPP 相關解算策略

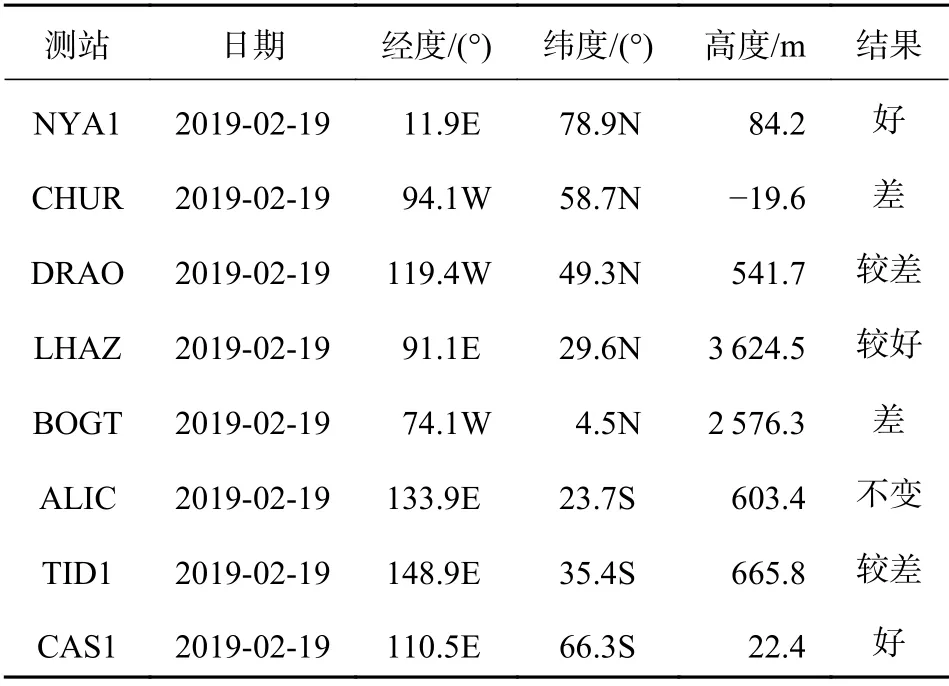
表2 均勻選取2019 年2 月19 日8 個IGS 測站信息及分析結果

為了進一步驗證這一想法，重新選取了高緯度地區6 個測站14 天的數據，南極和北極各3 個IGS站，其中THU2 測站由于數據缺失選取了其他時段，時長仍為14 天，測站信息如表3 所示.

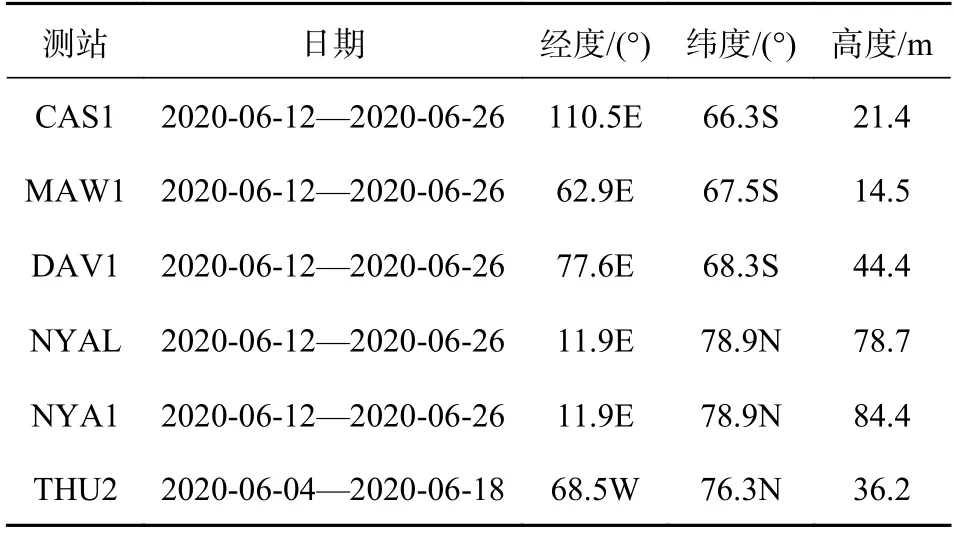
表3 高緯度IGS 測站信息

為比較不同隨機模型對高緯度地區PPP 的效果，圖1 給出6 個測站14 天的坐標均方根(RMS).

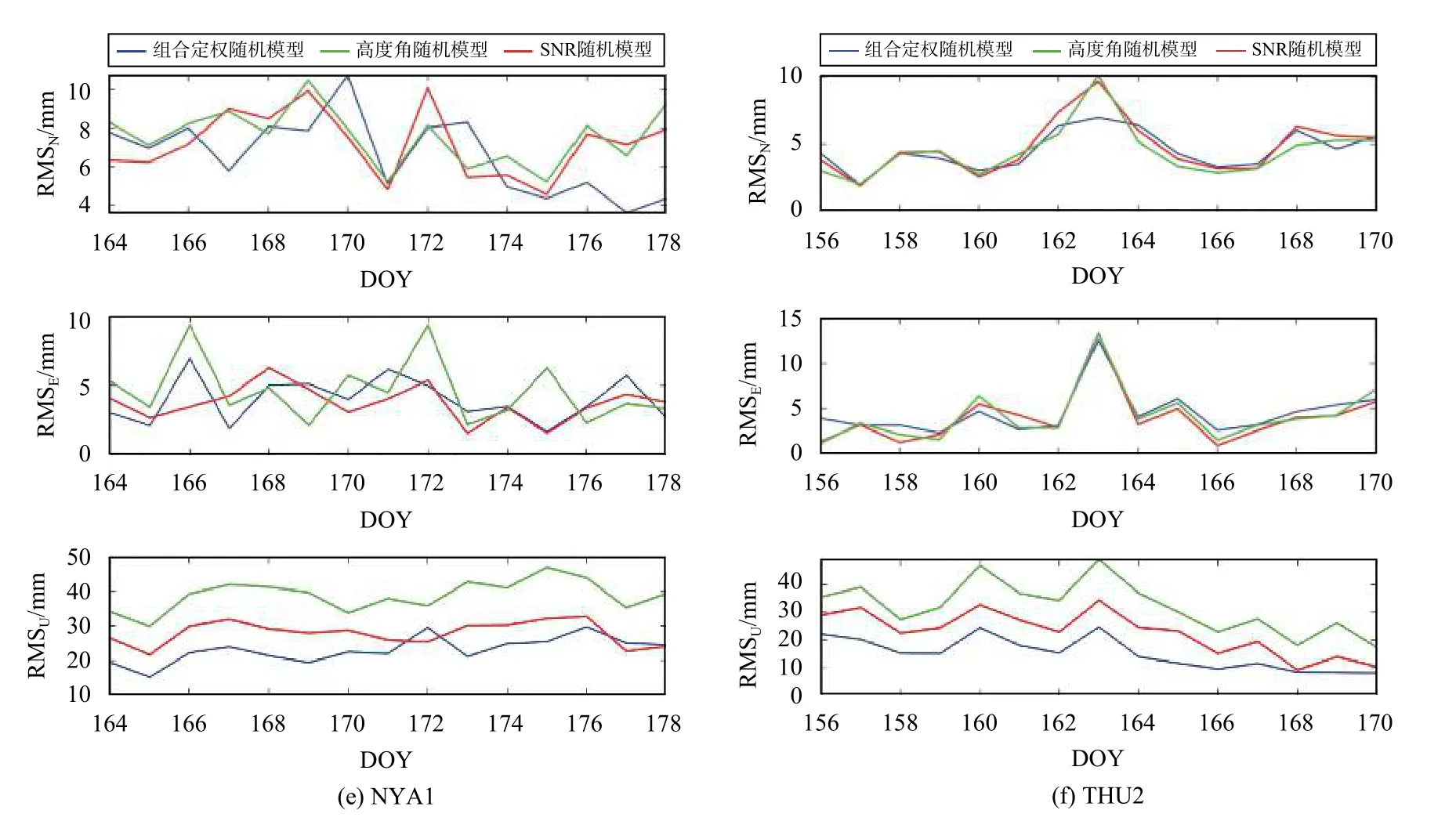
圖1 6 個測站的三種隨機模型定位結果在不同方向上的比較

從圖1 可以看出，精化隨機模型在天(U)方向上精度提高較大，在北(N)、東(E)方向上與只顧及高度角或SNR 的傳統隨機模型差別不大.PPP 平面位置精度可以達到mm 級，高程定位精度約為平面的1/3，因此U 方向是提高整體定位精度的關鍵.表4 給出了三種隨機模型在不同方向上的RMS 值以及精化隨機模型相對于其他兩種模型的精度提高率.

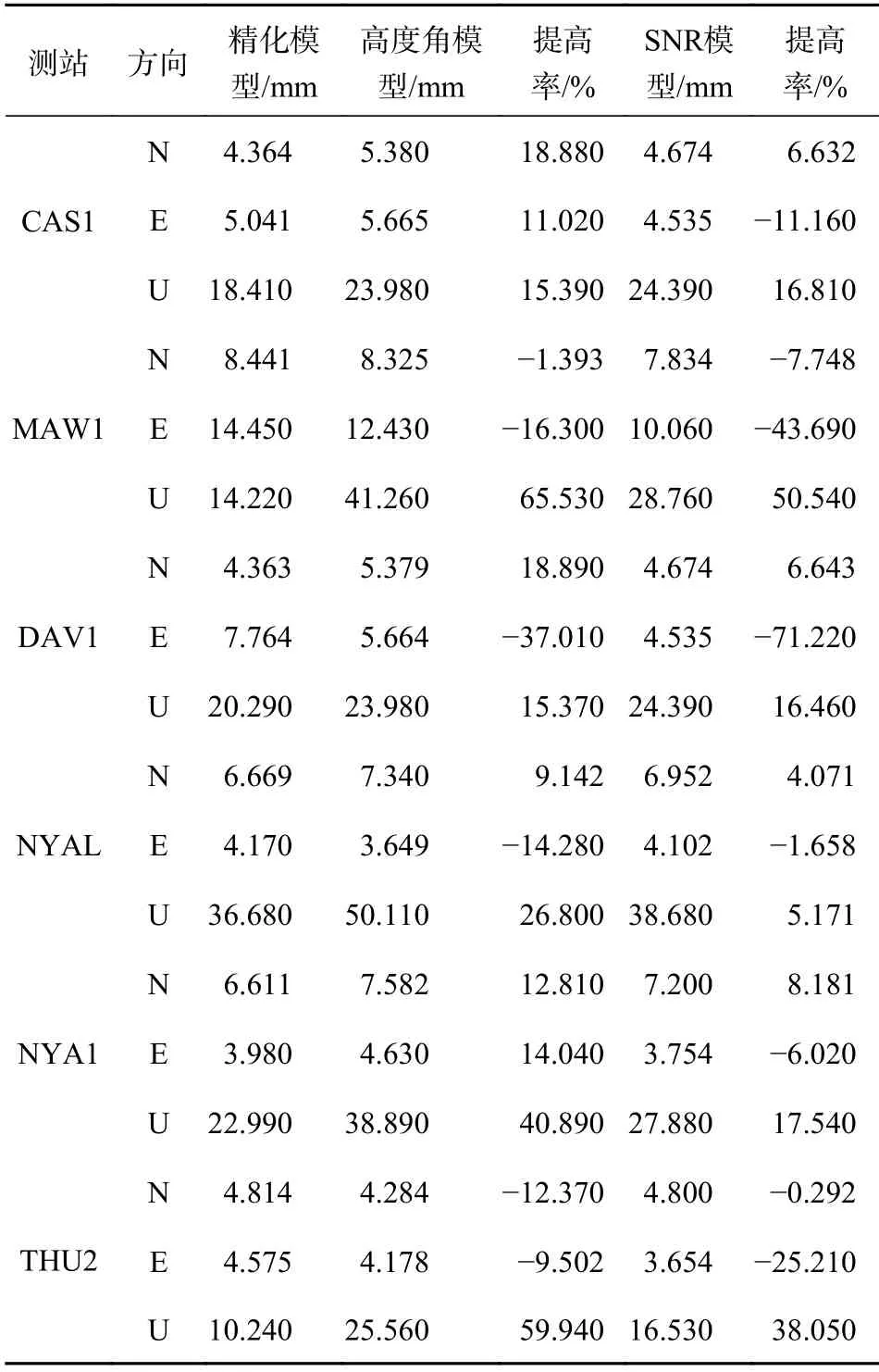
表4 南北極6 個IGS 測站在不同隨機模型中的PPP 精度的比較

由表4 可知，精化隨機模型相比于高度角模型對定位精度的提高率基本為正值.在U 方向上的提高率分別為15.39%、65.53%、15.37%、26.80%、40.89%和59.94%；在N、E 方向上的提高率大部分約在10%～20%，其中MAW1 測站以及THU2 測站的N、E 方向和NYAL 以及DAV1 測站的E 方向上的提高率為負值.這種情況是由于精化隨機模型此時在此測站的水平定位精度不及高度角模型或SNR 模型，主要原因是數據質量有多路徑誤差的影響，并且南極地區可觀測衛星數較少，正弦函數隨機模型并不能準確地描述數據質量隨高度角的復雜變化，因此在之后的研究中考慮加入位置精度因子(PDOP)值進行改善.但精化隨機模型的三維定位結果在可接受范圍內，說明精化隨機模型完全可以在高緯度地區的高精度定位中代替高度角模型并提高定位精度.精化隨機模型較信噪比模型的定位精度提高率不及高度角模型明顯，但在U 方向上也均為正值，分別為16.81%、50.54%、16.46%、5.171%、17.54%以及38.05%.U 方向上定位精度為cm 級，因此在N、E 方向上mm 級定位精度的效果被放大了，下面將在表5 中給出六個測站的三維點位精度及精化隨機模型相比于其他兩種傳統隨機模型定位精度的提高率.

由表5 可知，精化隨機模型較高度角模型的三維定位精度提高了約10%～50%，NYA1 站的效果最好，為53.52%；較SNR 模型提高約5%～30%，THU2站效果最顯著，為30.64%.

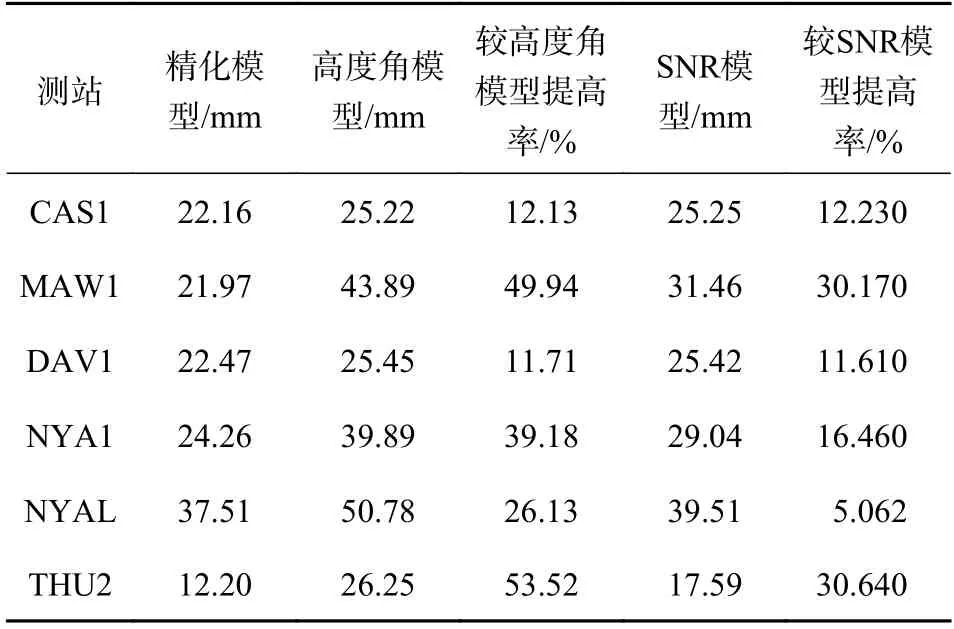
表5 6 個IGS 站在3D 方向上不同隨機模型定位精度比較

為進一步分析精化模型對高緯地區PPP 的改進效果，選取該地區5 個測站2016—2019 年每年1 周的數據進行研究，定位結果如圖2 所示，橫軸為年積日，縱軸為PPP 在U 方向上的平均中誤差.精化隨機模型在N、E 方向上的效果與傳統隨機模型相近，改善U 方向上的定位精度才是亟待解決的問題.

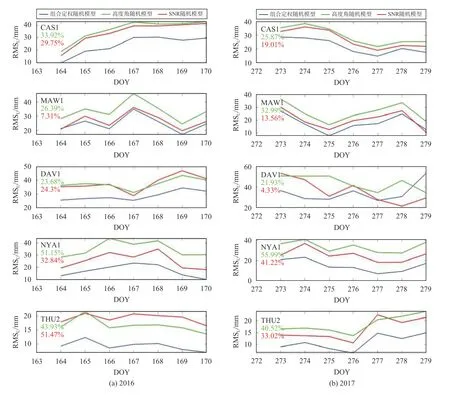
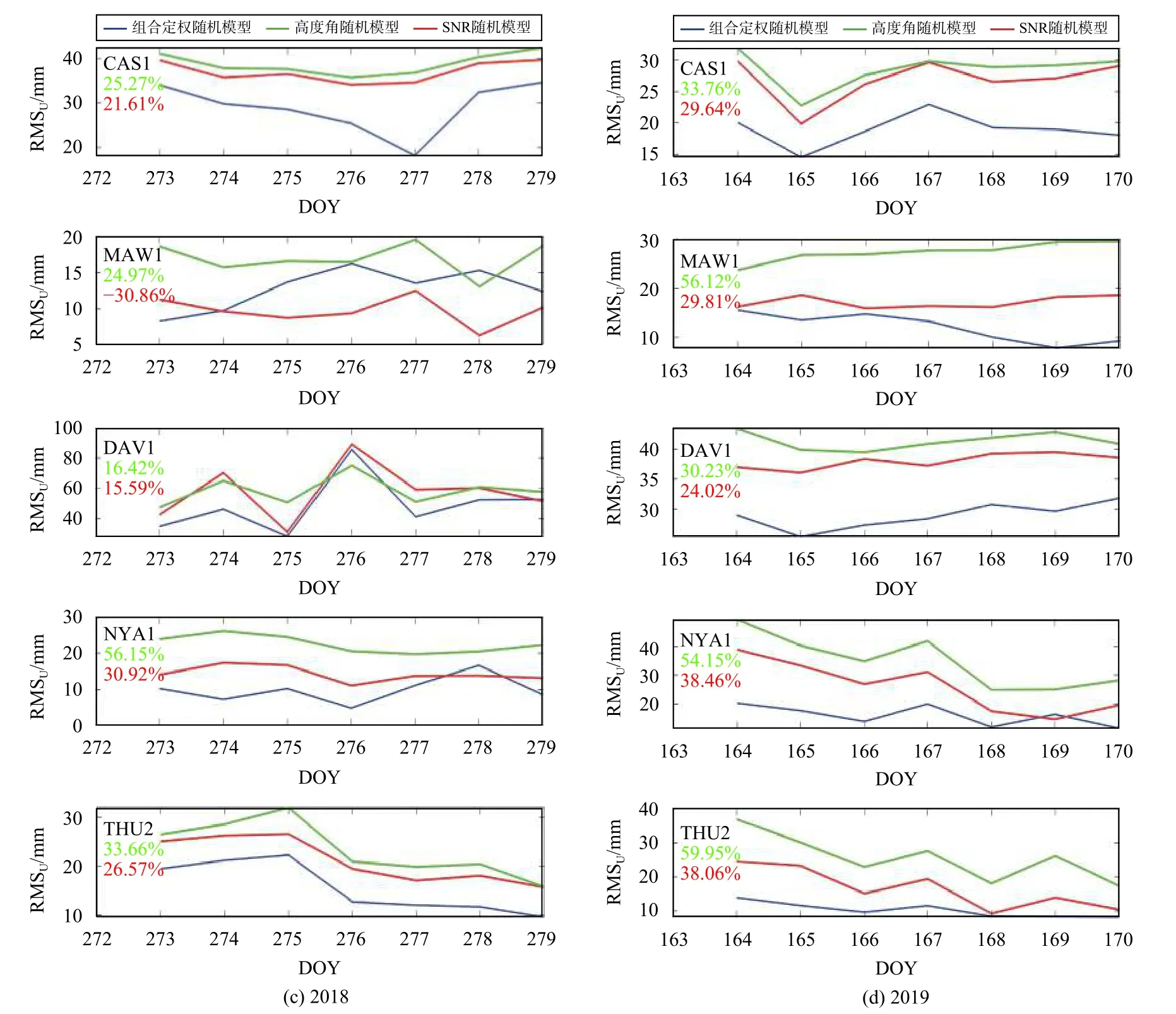
圖2 5 個測站在2016—2019 年三種隨機模型在U 方向上的定位精度比較

如圖2 所示，絕大多數情況5 個測站的精化隨機模型效果優于僅考慮高度角或SNR 的傳統隨機模型.圖中綠色百分數為精化模型較高度角模型的提高率，整體提高約37%；紅色百分數為較SNR 模型的提高率，整體提高約24%.精度提高較大的測站是CSA1站和THU2 站.

可以看出2016—2020 五年的數據中精化隨機模型更加穩定，并且另三個測站的結果也驗證了精化隨機模型能夠在一定程度上提高PPP 的定位精度.因此，本文提出的精化隨機模型在高緯度地區測站實施PPP 效果要明顯優于其他兩種隨機模型.

精化隨機模型在高緯度測站的PPP 解算中保持了較好的穩定性，在U 方向上的定位精度優于僅考慮高度或SNR 的傳統隨機模型.只有2018 年在DAV1 測站精化隨機模型的優勢不那么顯著，分析數據發現該時間段DAV1 測站的可見衛星數以及觀測環境較差，從圖2 中也可以看出其平均RMS 值較其他年份大了近一倍.通常情況下，高度角模型的定位結果精度是不及SNR 模型的，圖2 也進一步驗證了這一說法，我們可以看出：PPP 的隨機模型中，使用高度角模型的定位結果最差，SNR 模型次之，而精化隨機模型的精度要高于二者.

4 結 語

本文利用PCA 確定了GNSS 觀測噪聲中高度角和SNR 的貢獻，建立了精化隨機模型，通過對高緯度地區IGS 站實施PPP 的效果進行分析，得到了如下結論：

1)對比高緯度測站的PPP 定位結果來看，U 方向上精化隨機模型的RMS 值最小，定位精度最高，SNR 隨機模型次之，高度角模型效果最差.精化隨機模型的三維點位精度較高度角隨機模型提高約30%，較SNR 隨機模型提高20%左右，將該模型應用于高緯度地區PPP 解算可以有效地提高定位精度且計算量沒有增加.

2)在驗證過程中出現了精化隨機模型水平定位精度不及高度角或SNR 模型的情況，精化隨機模型不及高度角定權時，由于衛星星座結構較好，衛星數據的質量基本隨高度角的增加而提高，低高度角衛星的數據質量受多路徑誤差影響，此時加入SNR 所確定的權重可能會破壞解算質量；不及SNR 定權結果時，雖然低高度角數據質量較差，但考慮到南極區域可觀測衛星數量較少，利用低高度角觀測能增加可觀測衛星數量，此時正弦函數模型便不適用了.因此高度角和SNR 還不能全面地評價觀測數據的質量，在今后的研究中我們考慮將PDOP 值納入到評價指標中，利用PCA 做進一步的分析和降維處理，以完善和驗證本文方法.