基于直立長方體模型的山體隆升與重力變化關系數值模擬

梁晨昊 申重陽 王嘉沛

摘要：基于形變與密度變化耦合運動理論，利用時變場內重力垂直梯度的計算方法，采用直立長方體模型，根據青藏高原平均降升速率，模擬計算在艾黎地殼均衡模式下，地表形變所引起重力及其垂直梯度的變化。結果顯示，在山體抬升過程中，伴隨著地表的隆升，重力值亦逐漸減小，導致其減小的原因為介質體密度減小與測點的高度增加。伴隨著山體最高點抬升了5 cm，在最高點處重力變化為-14 μGal，對應的重力梯度約為-2.6 E。重力垂直梯度與靜態場重力梯度存在一定的差異，其原因為在重力梯度場中加入了時間效應。

關鍵詞：耦合運動;地表形變;重力變化;重力垂直梯度

中圖分類號：P315.721?? 文獻標識碼：A?? 文章編號：1000-0666（2021）02-0162-08

0 引言

20世紀70年代以來，重力、水準、GNSS等觀測技術不斷進步，觀測精度不斷提高，目前，GNSS觀測以及水準測量精度可達到毫米級別，重力測量精度亦可達到微伽。近年來，我國的大陸重力與GNSS觀測網的時空分辨率有了大幅度提升（李強等，2012;申重陽，2005）。現階段的GNSS和重力觀測所提供的數據，可以很好地將重力與形變相結合，用來探究地殼運動及地震機理，取得了許多研究成果，特別是在青藏高原地區隆升與重力變化關系的研究中（邢樂林等，2017;段虎榮等，2020），形變與重力數據的結合發揮了很好的作用。但在研究過程中，依然存在兩者數據結合不足的情形。

因此，將形變與重力數據更好地結合，研究兩者之間的關系，探究重力變化機理及其與形變的關系成為現代地球物理學與大地測量學的研究熱點。自20世紀以來，已有不少學者在理論上對其進行了初步的探究，Walsh（1975）首先推導出形變引起重力變化的計算公式，率先從理論上進行了分析。Reilly和Hunt（1976）指出了Walsh所得結果的錯誤，并給出了地球表面固定不變時形變所引起的重力變化，在該研究的基礎上，陳運泰等（1980）完善了形變引起的重力變化理論，給出了區域形變和物質遷移引起的重力變化效應公式。李瑞浩（1988）采用不同原理，推導出和陳運泰等（1980）一樣的結果。上述研究結果只適用于準靜態變形情形，尚沒有真正涉及形變時變模型。為此，申重陽和李輝（2005）提出了地殼變形與密度變化的耦合運動的思想與理論，給出了地殼變形與密度變化的耦合運動產生的重力場時變公式。王嘉沛等（2015）結合形變與密度變化耦合運動理論，利用直立長方體模型和川滇地區GNSS水平運動觀測結果，模擬計算了該地區水平運動對空間固定點所產生的重力效應，但尚未考慮垂直運動效應和地表固定觀測點伴隨地表運動的情形。同時，對于山脈地區的形變研究，邢樂林等（2017）和段虎榮等（2020）分別利用重力變化數據研究了青藏高原的地殼增厚和隆升速率，但沒有考慮到在伴隨著青藏高原隆升過程中，地殼內部介質的密度是否發生變化。

因此，本文基于形變與密度變化耦合理論，運用直立長方體重力異常模型，模擬計算在山體隆升運動（以青藏高原為例）下產生的重力時變效應，計算在時變場內重力垂直梯度的變化，并對形變、密度與重力之間的時變關系作進一步研究。

1 基礎理論

1.1 介質體形變所引起的重力變化的一般表達式

地殼形變會引起介質體質量的重新分布，從而引起重力變化。一些學者（Walsh，1975;陳運泰等，1980;申重陽等，2005，2007）從理論上分析了形變與重力變化的關系，為后面的模擬計算提供了理論依據，即以地心為原點（0，0，0）（定點），設置相對地球的慣性直角坐標系（x，y，z）。地球內部時刻發生運動，對于任意時刻t，設地球物質的集合為Ω（t）， 地球表面用S（t）表示， S（t）同時包含了地球表面和地球內部洞穴的表面。假設，在S（t）上存在任意一點P0， 其坐標設置為（rs，t），其中rs=xsi+ysj+zsk。在地球內部存在一個任意點Q（r，t）∈Ω（t），其中r=xi+yj+zk，點的密度減和位移可表示為ρ（r，t）≠0和u（r，t），在Q點的形變速度可用位移u（r，t）對時間的一階導數來計算u·（r，t）。將Q到P之間的向量關系表示為：R=r0-r，其數值大小表示為：R=r0-r。

整個地球運動過程均滿足質量守恒定律，我們將以地球內部任意點Q為中心的介質體元設置為dv（r），其密度變化為：

1.3 模擬山體形變模型

山體在隆升過程中，對其周圍地區的地貌會產生很大的影響，同時也會發生形變作用，從而引起相應的重力變化。根據形變引起的重力變化的一般表達式以及質量守恒定律可知，介質體在發生形變作用的同時會伴隨著密度的變化。研究山體隆升運動所產生的重力變化時應結合形變與密度變化耦合理論，應遵循質量守恒定律。

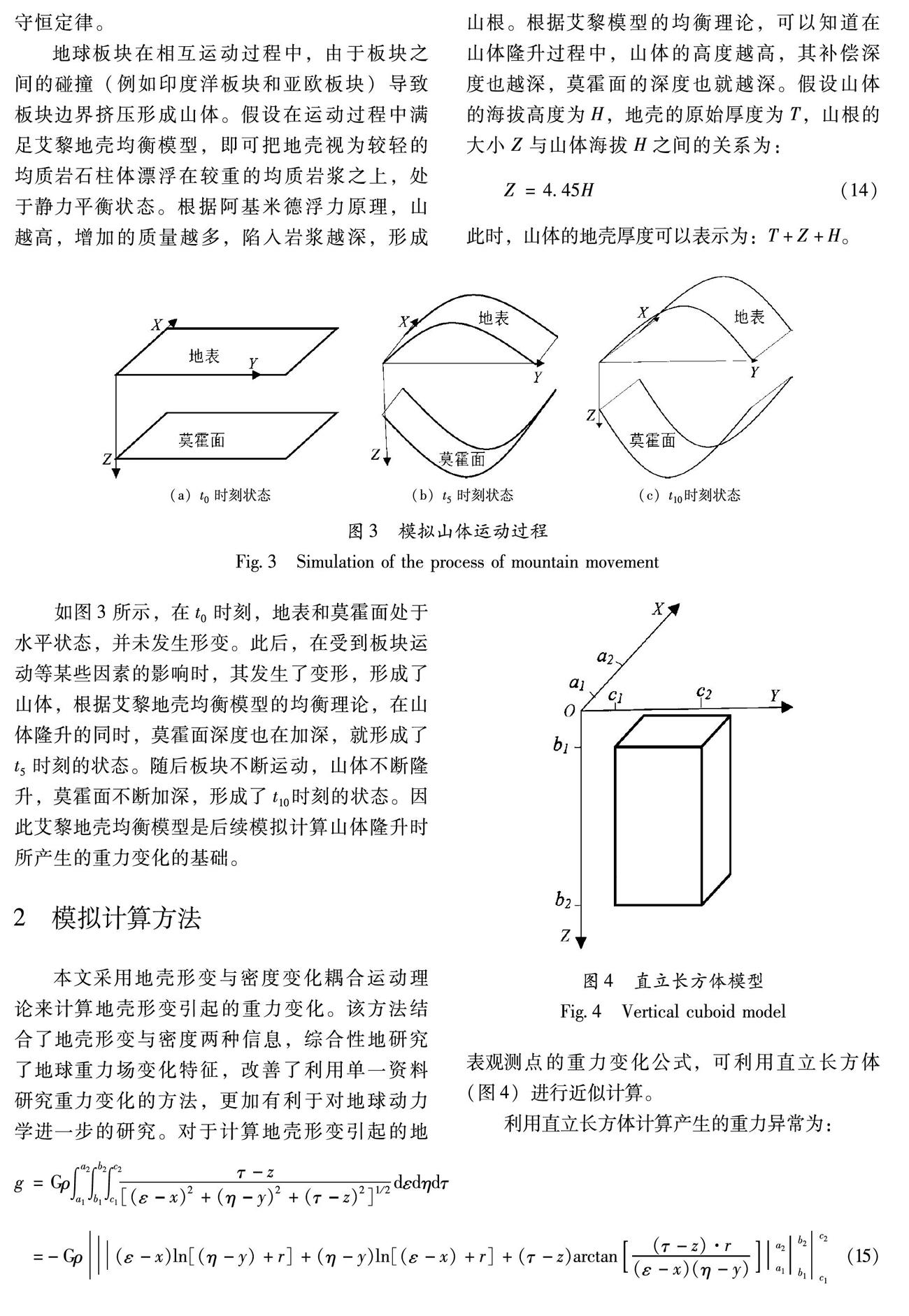
地球板塊在相互運動過程中，由于板塊之間的碰撞（例如印度洋板塊和亞歐板塊）導致板塊邊界擠壓形成山體。假設在運動過程中滿足艾黎地殼均衡模型，即可把地殼視為較輕的均質巖石柱體漂浮在較重的均質巖漿之上，處于靜力平衡狀態。根據阿基米德浮力原理，山越高，增加的質量越多，陷入巖漿越深，形成山根。根據艾黎模型的均衡理論，可以知道在山體隆升過程中，山體的高度越高，其補償深度也越深，莫霍面的深度也就越深。假設山體的海拔高度為H，地殼的原始厚度為T，山根的大小Z與山體海拔H之間的關系為：

Z=4.45H（14）

此時，山體的地殼厚度可以表示為：T+Z+H。

如圖3所示，在t0時刻，地表和莫霍面處于水平狀態，并未發生形變。此后，在受到板塊運動等某些因素的影響時，其發生了變形，形成了山體，根據艾黎地殼均衡模型的均衡理論，在山體隆升的同時，莫霍面深度也在加深，就形成了t5時刻的狀態。隨后板塊不斷運動，山體不斷隆升，莫霍面不斷加深，形成了t10時刻的狀態。因此艾黎地殼均衡模型是后續模擬計算山體隆升時所產生的重力變化的基礎。

2 模擬計算方法

本文采用地殼形變與密度變化耦合運動理論來計算地殼形變引起的重力變化。該方法結合了地殼形變與密度兩種信息，綜合性地研究了地球重力場變化特征，改善了利用單一資料研究重力變化的方法，更加有利于對地球動力學進一步的研究。對于計算地殼形變引起的地

表觀測點的重力變化公式，可利用直立長方體（圖4）進行近似計算。

利用直立長方體計算產生的重力異常為：

3 模擬計算結果

本文通過數值計算分析青藏高原以5 mm/a（邢樂林等，2017;段虎榮等，2020）的速率隆升時所產生的重力變化，時間步長取10 a，初始時刻為t0，t5時刻表示以t0時刻為基礎山體隆升5 cm之后的狀態，t10時刻表示以t0時刻為基礎山體隆升10 cm之后的狀態，分別測量t5和t10時刻重力以及重力梯度分布。在計算時由于密度會隨時間和位置變化，設置初始密度為ρ=2.67 g/cm3，在隆升過程中所產生的密度變化可利用式（2）計算求得。假定地表隆升形變范圍為（50×50）km2。觀測網大小定位（70×70）km2，這樣可以將形變區域完全覆蓋，在計算時將地表劃分為（0.5×0.5）km2的網格。在計算過程中假設每個塊體密度都是均勻的，其密度變化也是均勻的。

本文計算得到了形變過程中地表介質重力分布。在初始狀態（t0時刻），地表未發生形變，密度均勻，其地表重力分布如圖6所示。t5時刻，由于板塊運動等作用，地表發生隆升形變。t5時刻對應的重力及重力變化情況如圖7a所示。從圖中可以看出，在山體隆升5 cm所產生的重力差值為-14 μgal。t10時刻，地表隆升形變還在持續，隆升速度與前一個時間段相同，其對應的重力及重力變化值如7b所示。同時，利用式（13）分別計算了在地表隆升過程中（t0～t5，t5～t10時段）山體的地表重力垂直梯度，如圖8所示。從圖8中可以看出山體的大致形狀。在山體地區，重力垂直梯度約為-2.6 E，在山體周圍的地區重力垂直梯度較大，約為-5 E。在t0～t5和t5～t10時段山體隆升運動過程中，山體隆升的量級相同，所以在運動過程中所產生的重力變化和重力梯度相同，同時重力變化和重力垂直梯度的空間分布情況同模擬的山體空間分布情況一致，因此導致兩次運動過程的重力差值和梯度圖像相同。

4 結論

本文基于形變與密度變化耦合運動理論，給出了在時變場里重力垂直梯度計算公式的表達形式，并利用直立長方體模型模擬山體在抬升過程中所產的重力變化以及重力垂直梯度的變化情況，主要得到以下結論：

（1）在山體抬升運動過程中，由于形變與密度變化耦合，形變即發生密度變化。因此，利用質量守恒定律所求得的山體密度在海拔高的地區較小。在山體抬升過程中，密度值逐漸減小，觀測點與介質的距離逐漸增加，導致重力值逐漸減小。第一個時間段內（t0～t5），地表抬升5 cm，其重力梯度約為-2.6 E。在第二個時間段內（t5～t10），地表隆升5 cm，其重力梯度約為-2.6 E。在整體運動過程中地表隆升10 cm，重力垂直梯度約為-2.6 E，重力梯度分布與山體形態分布相同，重力垂直梯度與靜態場重力梯度存在一定的差異，其原因為在重力梯度場里考慮了時間效應。

（2）結合形變與密度耦合定律，模擬計算了在青藏高原隆升時，在密度變化的情況下，所產生的重力變化和重力垂直梯度的變化情況。計算結果顯示，青藏高原在兩次隆升過程中，重力梯度沒有發生變化，重力變化同時受到地表隆升和地下介質變動的影響。在研究青藏高原隆升時所產生的重力變化時，應當考慮密度變化和形變效應的雙重影響。

參考文獻：

陳運泰，顧浩鼎，盧造勛.1980.1975年海城地震與1976年唐山地震前后的重力變化[J].地震學報，2（1）：21-30.

段虎榮，康明哲，吳紹宇，等.2020.利用 GRACE時變重力場反演青藏高原的隆升速率[J].地球物理學報，63（12）：4345-4360.

李強，游新兆，楊少敏，等.2012.中國大陸構造變形高精度大密度GPS監測——現今速度場[J].中國科學：地球科學，42（5）：629-632.

李瑞浩.1988.重力學引論[M].北京：地震出版社.

申重陽.2005.地殼形變與密度變化耦合運動探析[J].大地測量與地球動力學，25（3）：11-16.

申重陽，李輝.2007.研究現今地殼運動和強震機理的一種方法[J].地球物理學進展，22（1）：49-56.

王嘉沛.2015.地殼變形與密度變化耦合運動引起的重力變化效應研究[D].北京：中國地震局地震研究所.

王嘉沛，申重陽，玄松柏.2015.全球地殼模型CRUST1.0在青藏高原東南部的重力檢核[J].大地測量與地球動力學，35（4）：621-626.

邢樂林，王林海，胡敏章，等.2017.時變重力測量確定青藏高原地殼隆升與增厚速率[J].武漢大學學報（信息科學版），42（5）：569-574.

Reilly W I，Hunt T M.1976.Comment on An analysis of local changes in gravity due to deformation by J B Walsh[J].Pure & Applied Geophysics，114（6）：1131-1133.

Walsh J B.1975.An analysis of local changes in gravity due to deformation[J].Pure & Applied Geophysics，113（1）：97-106.

Simulation of the Relationship between the Surface Deformationand the Gravity Variation Based on Vertical Cuboid

LIANG Chenhao，SHEN Chongyang，WANG Jiapei

（Key Laboratory of Earthquake Geodesy，Institute of Seismology，China Earthquake Administration，Wuhan 430071，China）

Abstract

Based on the coupling theory of deformation and density variation，the vertical gradient of gravity in time-varying field is calculated.By the help of the vertical cuboid and average uplift rate of the Tibetan plateau，the process of the mountain movement is simulated，and the variation of gravity and its vertical gradient caused by surface deformation is simulated in accordance with the Airy equilibrium model.The results show that in the process of mountain uplift，the gravity value gradually decreases.It is speculated that the gravity decrease is caused by the decrease of medium density and the increase of the height of the measuring point.The mountaintop where the maximum gravity value appears rises for 5 cm，as a result，the maximum gravity changes for-14 μGal，and the corresponding gravity gradient is about -2.6 E.Due to the time effect in the gravity gradient field，there is a certain difference between the vertical gravity gradient and the static gravity gradient.

Keywords：coupled motion;surface deformation;gravity variation;vertical gravity gradient

收稿日期：2020-12-25.

基金項目：國家自然科學基金項目（41674018）資助.

第一作者簡介：梁晨昊（1996-），碩士，主要從事形變重力解釋方面研究.E-mail：lch158768@163.com

通訊作者簡介：申重陽（1963-），研究員，主要從事形變重力解釋、地震前兆機理、地球物理場及其反演、工程地震等方面的研究.E-mail：scy907@163.com.