極區中層塵埃粒子的帶電效應

葛淑燦，李海龍*，蒙 林，王茂琰，RAUF Abdur，ULLAH Safi

(1. 電子科技大學電子科學與工程學院 成都 611731；2. 電子科技大學物理學院 成都 610054)

Polar mesosphere summer echoes (PMSEs) are strong radar echoes produced at polar latitude during the summer. This phenomenon is the first time observed with 50 MHz MST radar at Poker Flat,Alaska[1]. The occurrence altitude of PMSE is about 80～90 km, and the strongest echo is usually observed at about 85 km. Since its first observation at 50 MHz,PMSE have been observed at a variety of frequencies between 2.78 and 1 290 MHz. Many scientists of space and dusty plasma physics diverted their attentions to these interesting radar phenomena and achieved a lot of diagnostic information[2].

It is now well understood that charged ice particles play a crucial role in the charge balance of the polar summer mesosphere region where ice particles become negatively charged due to electron attachment and hence effectively scavenge electrons[3-9]. This process results in electron density depletions or the socalled electron ‘bite-outs’[10]. Fluctuations in electron density are generally anti-correlated to the negative dust charge density, however, in certain regions, it is also positively correlated[11]. Recently, in the Earth ionosphere the effect of charged dust particles on radar observations was discussed[12]. Also, a new method for the analysis of the measurements of mesospheric dust was presented[13]. The occurrence of ‘bite-outs’ is hence considered as strong support for the existence of mesospheric ice particles. So far, electron ‘bite-outs’ in the vicinity of PMSE have routinely been observed with the rocket-borne sensors[10,14-16]as well as occasionally with ground-based radars[17-18].

Study of dusty plasma is important for a number of applications in laboratory plasmas and modern plasma technologies, as well as in space plasmas and plasma of the Earth’s environment[19-20]. Scattering of electromagnetic waves in plasma is a powerful diagnostic method that has been successfully used in the laboratory and ongoing geophysical experiments[21-25].

Rocket experiments have been used to detect PMSE. In the rocket experiments, there is equipped with a dust probe (DUSTY) for measuring dust current and an electron probe (CONE) for measuring neutral atmospheric parameters and electron currents. When the rocket moves through the mesopause, the charged dust particles and electrons collide with the DUSTY and CONE probe respectively and generate current.Then the dust current and electron current were recorded. In addition, the temperature of the mesosphere can be measured[13,26-27]. However, in these experiments the radius and charge of dust particles are not measured accurately. But it is suggested that the dust charge number can be obtained by the charging process of electron and ion to dust particles. Later,PMSE heating experiments also detect the dust particles in the polar mesosphere, however, we still lack numerical simulation about the charged dust particles causing PMSE[28-29]. So, it is necessary to analyze the size of dust particles and estimate the electric charge by theory and simulation.

In this paper, using the orbit-limited motion(OLM) method and the charging theory of dust particles, the formula for dust charge is deduced in dusty plasma. The experimental data of ECT-02 is used to analyze the charge number of dust particle in the PMSE dusty plasma region (80～90 km).

1 Theoretical Model

In the mesosphere, since photoelectron emission is negligible, the charging process of electron and ion to dust particles is only due to the collection of plasma particles where the charge number on each dust particles will be low (typically a few unit charges or less) and negative. The OLM theory is one of the most popular sphere-charging model[30]. The OLM method is based on the electron/ion Maxwell distribution to decide the electron/ion current carried on dust particles[31-33]. The OLM method and the charging theory of dust particles in dusty plasma are used to obtain the relation of dust particles radius and dust charge number with different electron temperatures.When the active experiments of PMSE are carried out,the electron temperature will change greatly, and many other parameters in PMSE dusty plasma layer will have corresponding changes at different time scales.To the best of our knowledge, the charging effects of dust particles in polar has not been yet addressed within the experimental framework[34-36].

By using the OLM method, the charging current to the dust grain carried out by the plasma particles are given as:

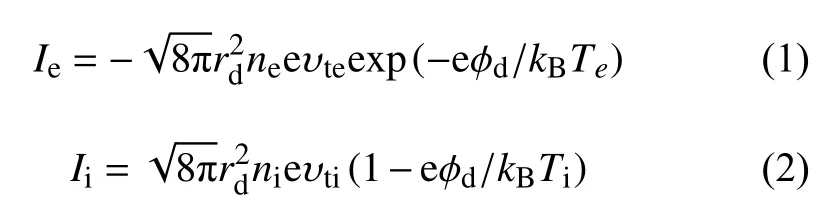
whereIeandIirepresent the charging currents of electron and ion, respectively;kB=1.38×10-23J·K-1is Boltzmann constant;rdand φdare the dust radius and floating potential;ne,me, andTeare the electron density, mass and temperature, respectively;ni,mi, andTiare ion density, mass and temperature, respectively;υte=(kBTe/me)1/2and υti=(kBTi/mi)1/2are the electron and ion thermal velocities, respectively.

The dust grain surface becomes negatively charged andIi＜＜Ie(sinceme＜＜mi) when the number density of electron and ion have great differences.However, in the case of electron ‘bite-outs’ condition when the ion density is much larger than electron density, the ion and electron currents have no difference given as:

When no external disturbance is present, like electron-ion plasma, the dusty plasma is also macroscopically neutral. It means that in equilibrium with no external forces present, the net resulting electric charge in dusty plasma is zero. Therefore, the equilibrium charge neutrality condition in dusty plasma can be written as:

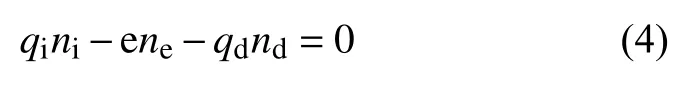
wherensis the unperturbed number density of the plasma species s (where s = ion or electron and d=dust);qiandqdare the charges of ion and dust,respectively. It is already confirmed that the dust particles in the mesosphere are mostly negatively charged.

We assume thatZd=-4πε0rdφd/e is the number of charges residing on the dust grain surface. Here,ε0is the permittivity of vacuum. At the same time, we assume that the ion charge stateZi=1 will be used in the rest of the paper. So equation (4) changes into:

By combining the obtained equations (1), (2), (3)and (5), it can be obtained:

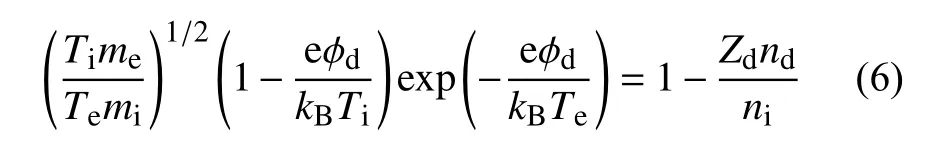
In the paper the unit ofrdis nm;TeandTiare the temperatures of electron and ion, with unit K,respectively. The mass of an electron isme=9.1×10-31kg and the mass of an ion ismi=4.98×10-26kg(where the main components are O2+and NO+,respectively). The charge of an electron is e=1.6×10-19C;Zdndis the dust charge number density.

Finally, the dust charge number is determined by the size of the dust radius, electron temperature, ion temperature, ion number density, and electron number density.

2 Numerical Model Results

For the analysis of radius and charge number of dust particles, the elementary parameters in the polar mesosphere, such as the electron density, dust charge number density, and temperature of dusty plasma are required. It is well known that all the parameters in the PMSE dusty plasma layer are affected due to active heating experiments, and the electron temperature shows the most obvious and immediate change with different radar frequencies and incident power.Therefore, the numerical model is built to analyze the relation between the average dust charge and dust charge number density. And the results of the numerical model are compared with information experiment results. The effect of dust radius on dust charge number density is given in Fig.1. From Fig.1,it is clear that the average dust charge decreases with an increase in dust charge number density. At the same time the average dust charge increases with an increase in dust radius.

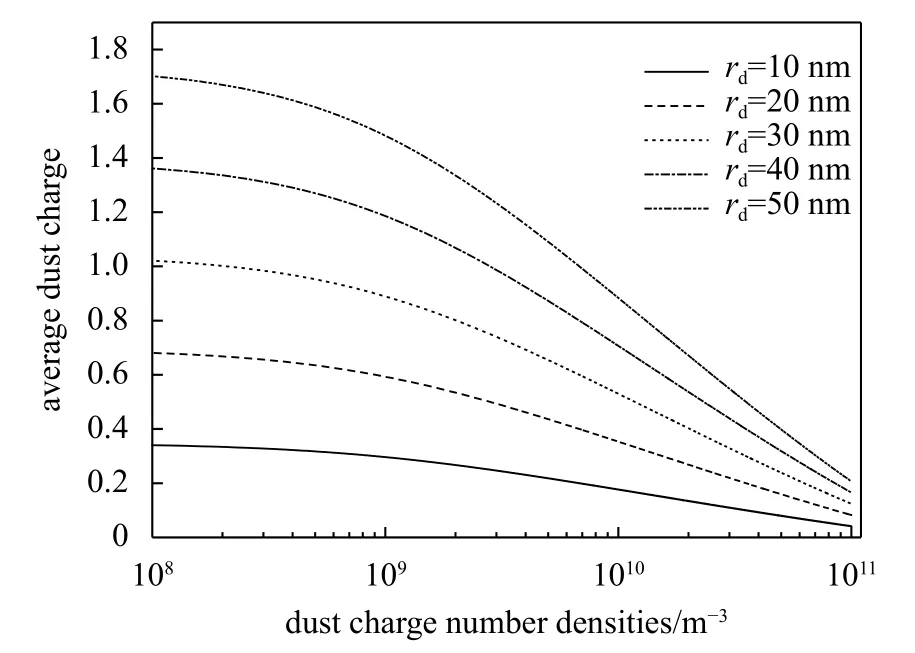
Fig.1 Dependence of average dust charge on dust charge number density with different values of dust radius

Fig.2 shows that the dependence of average dust charge on dust charge number density for different electron temperatures. It is clear that the average dust charge decreases with an increase in dust charge number density, and it increases with an increase in electron temperatures.

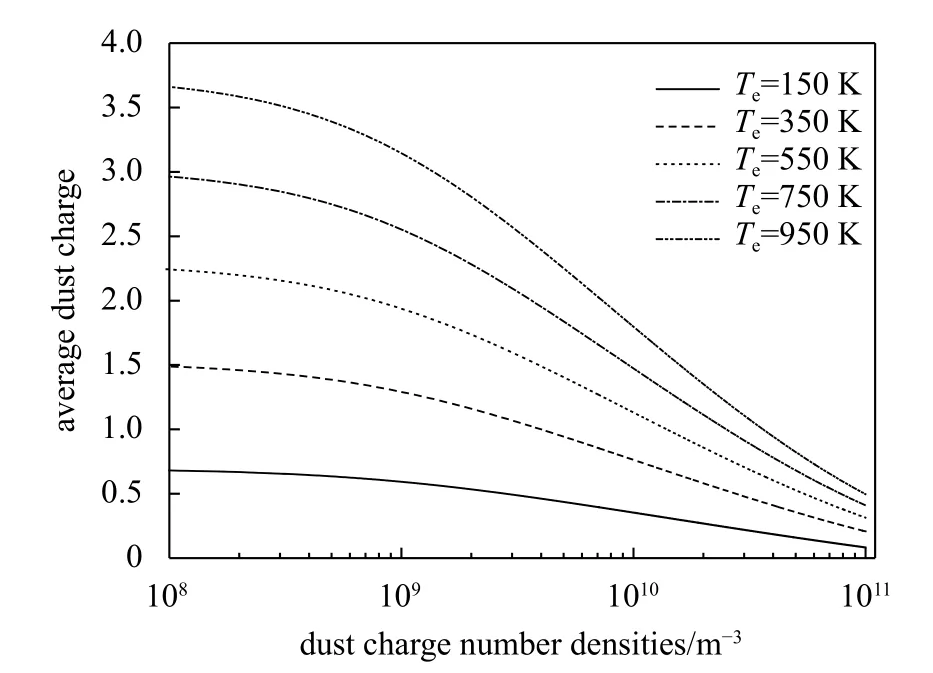
Fig.2 As Fig.1, but for electron temperature

Fig.3 gives the dependence of average dust charge on dust charge number density for different electron densities. It is clear that the average dust charge decreases with an increase in dust charge number density and increases with an increase in electron density. In addition, the decreasing tendency of average dust charge with an increase in dust charge number density is more and more slowly when the electron number density is larger.

Fig.3 As Fig.1, but for electron number density

3 Experiment Results

To study the PMSE, an international campaign ECHO-94 was conducted at And?ya Rocket Range(ARR; 69°N, 16°E), Norway, during the period July 25 to August 12, 1994. During the campaign, the EISCAT VHF (224 MHz) radar outside Troms?,Norway, and the ALOMAR SOUSY (50 MHz) radar located at ARR were used to detect PMSE. The first salvo (salvo 1; July 28-29, 1994) during ECHO was launched in the presence of strong PMSE detected by both radars. The results were named as ECT-02. The newer data are too difficult to gain because the data are not open source. However, the older data and the interpretation of them described in the paper are relevant for the interpretation and planning now underway. By analyzing the experiment of ECT-02,the atmospheric parameters such as neutral particles density, electron density, dust charge density, ion density, and temperature, were obtained. The range of height is 82～90 km. Two obvious electron ‘bite-outs’regions at height 85.5 and 87.5 km are shown in the Ref. [5]. Special attention is required at altitude range from 85.4 to 86 km. Here, the electron number density is too low to be detected by the Langmuir probe in the rocket. For convenient analysis, electron number densities in these heights were replaced by typical minimum values 1×105m-3observed by the EISCAT UHF radar.

Fig.4 shows the profile of average dust radius changing with average dust charge and altitude. It is clear that the radiuses show great differences in the region with electron ‘bite-outs’ and without electron‘bite-outs’. When the dust particles have one negative charge Zd=1 and no electron ‘bite-outs’, the radius of dust particles are no more than 40 nm which is larger than that given in Ref. [37].

Fig.4 Profile of average dust radius changing with average dust charge and altitude

To investigate the relation between average dust radius and average dust charges, we pay more attention to analyze the height from 87 km to 88 km with obvious electron ‘bite-outs’. Note that we do not analyze another electron ‘bite-outs’ region from 85.4 km to 86 km for avoiding the uncertain effect of electron density. The average radius from 87 km to 88 km are given in Fig.5. The dust charges are assumed as 0.3e, 0.4e, and 0.5e corresponding to black dotted, blue solid, and red dot lines, respectively. From Fig.5, it is found that the dust radius increases when the average dust charge increases. Besides, the largest dust radius occurs at 87.5～87.6 km regardless of how many charges are charged to the dust, and the tends of dust radius changing with charged dust at different altitude are the same. Ref. [28] shows that it is at variance with current theories of the charging of particles when assuming a fixed dust particle radius is 10 nm. In fact, our results clearly show that dust particle radius can be significantly larger than 10 nm,much larger even than 50 nm if the dust has large enough charges. To a certain extent, the average radius agrees with that given in Ref. [37] when the average dust charge is 0.4e.

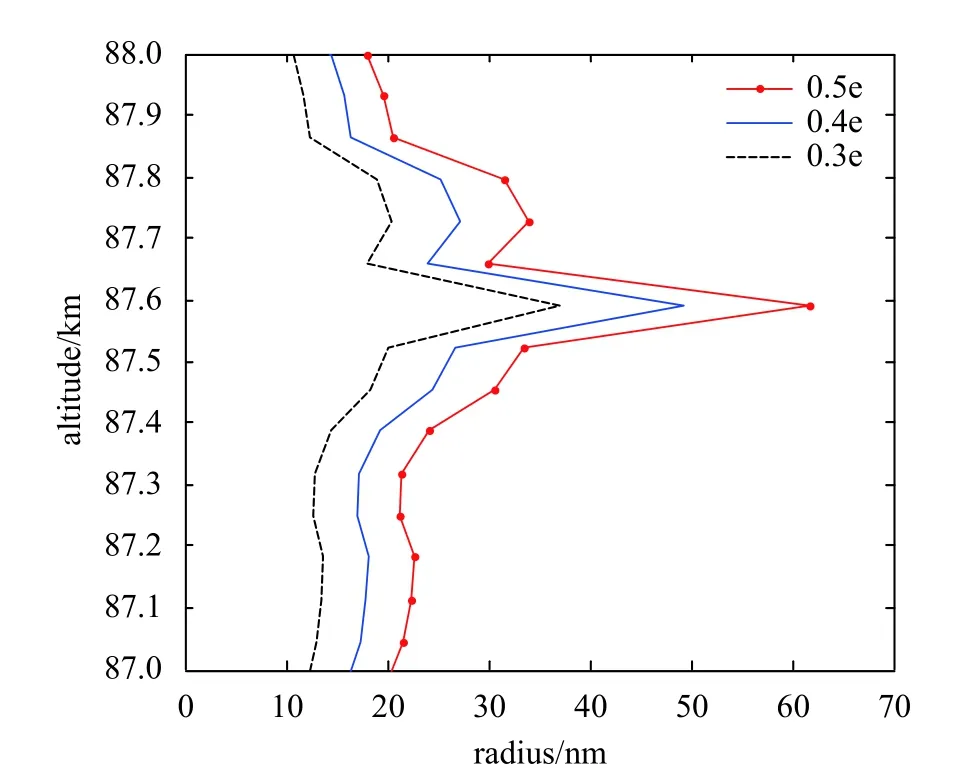
Fig.5 Altitude profile of average dust radius changing with average dust charges

4 Conclusions

In this paper, the formula for the dust charge number is deduced during heated PMSE condition. A simple but very useful method for the analysis of the dust charge number and the radius of dust particles in the polar summer mesosphere has been introduced.Dust charge number increases with an increase in dust radius, electron density, and electron temperature. In addition, the dust charge number decreases with an increase in dust charge number density. The simulation results are close to the current model results. Certainly,we can yield an indication of more benefits to be gained from a persistent approach to the extraction if we have new data as much as possible.