太陽能無人機能源系統的多維耦合建模

高明，余偉臣，王杉杉，王榮闖，石健將

浙江大學 電氣工程學院，杭州 310027

太陽能無人機作為一種新穎的高空飛行器，因其無污染排放、理論續航時間長等優點，受到多個飛行器制造企業和科研單位的廣泛關注[1-2]。它以柔性高效的光伏電池組件替代氫動力或汽柴油活塞動力裝置，直接將可再生的太陽能作為無人機的動力能源，這完全改變了無人機能源系統的構成形式，呈現出明顯的全電化特點，這也使得更多的電氣領域專業人員參與到太陽能無人機能源系統及能量管理器的研究當中[3-4]。

與地面光-儲發電系統相比，太陽能無人機的能源系統具有類似的硬件構成，均由通過導線互連的光伏電池、蓄電池和電源控制器組成[5]。但是地面光-儲系統的運行，尤其是光伏電池的運行，僅受到地表太陽輻照和地面氣溫的影響；而太陽能無人機能源系統的運行不僅受無人機所處海拔的太陽輻照和氣溫影響，同時自身飛行姿態的改變也使得布置在機翼上的光伏電池受光角度發生變化，從而影響光伏電池發電功率。能源系統的運行與大氣環境和飛行姿態間所呈現出的強耦合特征，使得太陽能無人機的能源系統和能量管理器設計，尤其是能量管理算法的開發和驗證工作與地面系統相比更為復雜，對于能源系統建模的準確性要求也更高。

國內外對于無人機能源系統的建模研究已有一定成果：文獻[6]給出了太陽能飛機的一套總體設計方法，其中解釋了各個主要模型之間的基本關系；文獻[7-8]以質量為耦合點，建立了太陽能無人機的質量與能量平衡模型，可作為能源系統的基本性能估算依據；文獻[9]對影響太陽能無人機光伏電池發電功率的因素進行了定性研究，但是缺少數學表達，對于能源系統設計的指導意義仍然有限；文獻[10]參考太陽能飛艇將光伏電池投影到坐標面，建立了太陽能無人機光伏電池隨姿態變化的關系模型，但是僅將偏航角與俯仰角納入到能源系統建模中，對于滾轉角則沒有考慮；文獻[11]開展燃料電池無人機的能量管理與飛行狀態耦合研究，建立了燃料電池無人機的耦合系統模型，但缺少光伏電池的參與，無法直接套用在太陽能無人機中；文獻[12]研究混合動力無人機的模糊能量管理策略，并建立了完整的無人機姿態角度與光伏電池的耦合模型，但沒有考慮到飛行高度變化對產能和耗能的影響；文獻[13]針對太陽能/氫能無人機能源系統，給出了一種耦合設計方法，并開發了一套仿真平臺，但未考慮到大氣環境和飛行姿態對能源系統的耦合影響，且仿真軟件未能與地面實物充分結合，對于提升能源系統驗證工作的準確性仍然有限；文獻[14]從地理位置、表面溫度、飛行日期的角度研究了無人機飛行狀態對光伏電池的影響，但忽略了無人機飛行姿態對電池受光量的影響。

由于現有研究中缺少對太陽能無人機能量流的完整模型描述，尤其是完整耦合外部大氣環境和無人機飛行姿態變化的建模研究，這不利于太陽能無人機能源系統、能量管理策略設計與驗證工作的開展，同樣不利于太陽能無人機地面半實物仿真平臺的搭建工作與價值體現。本文在上述研究工作的基礎上，完善模型中大氣環境和飛行行為對能源系統運行的耦合關系，建立考慮外部大氣環境和無人機飛行行為的能源系統耦合模型，并通過仿真結果說明不同因素對能源系統運行的耦合影響，最后給出了基于該模型搭建的半實物仿真平臺設計方案，為在地面進行太陽能無人機能源系統及其能量管理器的開發與驗證工作提供了一條低成本、快速、準確的途徑。

1 能量流耦合特性

太陽能無人機的能源系統作為能量產生、儲存、變換、調節和分配的系統，保證無人機動力和任務載荷所需能量的不間斷供給，實現能量耗用與生產的循環流動，可謂太陽能無人機的“心臟”，其典型構成如圖1所示，主要包含3個部分：① 光 伏電池為發電單元；② 蓄電池為儲能單元；③ 由開關電源電路和數字控制電路構成的能量管理器。此外，動力負荷在能源系統的建模過程中往往也被考慮進來，這是因為動力負荷是能源系統的主要耗能對象，有時也需經動力裝置將多余電能轉為高度勢能來儲能，同時也考慮到動力負荷耗能的結果是無人機的位置和姿態發生了變化，從而又反過來使光伏電池的發電水平產生了變化，形成了能量的閉環回路。

圖1 太陽能無人機及其能源系統

太陽能無人機能源系統的運行不僅受到大氣環境中光照、溫度等因素的影響，無人機的飛行狀態也會影響到能源系統的能量獲取與耗用。具體的講，能源系統以電能作為能量的交互形式，但整個能量流動過程則涉及到太陽能、化學儲能和高度勢能等多種能量形式的變化，具有多異質能流的特點，如圖2所示。不同能量流通過電功率的形式間接體現了各自的變化特性，這使得能源系統中電能的變化特性不僅僅與發電、用電裝置有關，同時還與其他能量形式所在的維度存在著強耦合關系，包括：

圖2 太陽能無人機的不同能流形式

1)外部大氣環境

① 太陽輻照隨時間流動而變化，同時隨無人機的所處位置(經度、緯度、海拔)而改變；大氣溫度同樣與無人機的位置有關，而太陽輻照與溫度是影響光伏電池發電功率的主要因素。

② 無人機所處位置的大氣密度與氣動力、氣動力矩和螺旋槳的推力呈相關關系，使得在不同海拔下達到相同作用力與飛行速度所需要的電機功率也有所不同。

2)無人機飛行姿態

① 光伏電池通常布置在無人機機翼上，無人機的飛行姿態(導航角、俯仰角、滾轉角)直接影響到光伏電池的受光面與入射光的相對角度，進而影響到了光伏電池的發電功率。

② 無人機的姿態角會影響機體受力與力矩平衡，為了使無人機保持飛行穩定，電機出力也會改變，從而影響能源系統的耗能過程。

為了對太陽能無人機的能量流動過程進行準確的描述，有必要將上述耦合作用考慮在內，建立考慮外部大氣環境維度和無人機飛行行為維度的能源系統多維耦合模型。基于該模型可以量化的反映出太陽能無人機中能量流的變化過程，有利于提高計算機仿真解算過程和地面半實物仿真平臺試驗過程的準確性。

2 多維耦合模型

圖3給出了模型的內部耦合關系，整個耦合模型的構成包括：非均質大氣環境模型、太陽輻照模型、無人機六自由度運動模型、電機模型、減速器模型、螺旋槳模型、光伏電池模型、蓄電池模型。下面分別建立上述模型。

圖3 能源系統模型的內部耦合關系

2.1 非均質大氣環境模型

太陽能無人機的飛行高度通常設計在幾百米到幾十千米的高空，在如此大的海拔跨度下，大氣的溫度變化使得大氣分子濃度和大氣密度也呈現出明顯的分布特點。非均質大氣模型在假設大氣均勻混合、同一離地高度的大氣分子濃度和大氣層密度相同的條件下，建立了大氣分子濃度和大氣密度隨高度變化的數學描述[15]。主要使用的大氣參數包括：

1)大氣溫度T

(1)

式中：T為距離海平面高度為zg(單位：km)時的大氣溫度；T0為海平面平均溫度，其值為15 ℃(288.15 K)；T11為距離海平面11 km(對流層的平均厚度)的大氣溫度，其數值為-56.5 ℃(216.65 K)；aT為溫度隨大氣高度的降低速率，其數值為6.5 K/km。

2)大氣壓強pa

(2)

式中：ma為空氣平均分子質量，為28.97 g/mol；R為氣體常數，為8.314 4 J/(K*mol)；g為重力加速度，為9.81 m/s2；p0為海平面的大氣壓強，為101 300 Pa；p11為距離海平面高度為11 km處的大氣壓強，為22 631.8 Pa。

3)大氣密度ρ

(3)

大氣密度與大氣壓強保持相同的變換關系，因此標準大氣的大氣密度可表達為

(4)

式中：ρ0為海平面的大氣密度，其數值為1.29 kg/m3；ρ11為距離海平面11 km處的大氣密度，約為0.297ρ0。

4)大氣分子濃度n

大氣分子濃度與大氣密度成正相關關系，有

n=γρ

(5)

式中：γ為比例系數，取γ=n0/ρ0，n0為海平面的大氣分子濃度，約為0.044 64 mol/L。

2.2 太陽輻照模型

大氣層對太陽輻照的光吸收作用會隨著大氣分子濃度的變化而改變，這是導致太陽輻照隨海拔高度變化的直接原因。考慮高度變化的太陽輻照模型的建立過程如下。

1)地球-太陽距離系數f

由于地球的公轉軌道是一個橢圓，因此一年中地球與太陽間的距離是不斷變化的，利用地球-太陽距離系數f來表征這種變化：

f=1+0.033cos(2πnday/365)

(6)

式中：nday為日序，即一年中的第幾天，nday=1指1月1日，nday=365指12月31日，以此類推。

2)大氣層外太陽輻射G

對于從太陽到地球大氣層外的全波長輻射G，可利用太陽常數和地球-太陽距離系數求得

G=S0f=S0[1+0.033cos(2πnday/365)]

(7)

式中：S0為太陽常數，其值為1 353 W/m2。

3)大氣層內太陽輻照S

對于地球大氣層內的全波長輻射S，可通過式(8)計算[15]：

(8)

式中：C體現了非均質大氣環境下的大氣層光吸收作用;A為大氣層的平均摩爾吸收系數，其取值與天氣狀況和大氣層的分子濃度與大氣層高度有關，可通過式(9)求取：

(9)

式中：βa為大氣層吸光度，晴天時βa<0.08；多云時0.08<βa<0.12；陰天時βa>0.12。n11、n20、n50分別為海拔為11、20和50 km處的大氣分子濃度；h11、h20、h50和h100分別為海拔11、20、50和100 km(通常認為海平面以上100 km為大氣層與外太空的分界，假設太陽輻射在外太空中沒有損失);φ為天頂角，表征一天內光照角度的變化：

cosφ=sinLasinτ-cosLacosτcos(πts/12)

(10)

式中：La為計算地點的緯度；τ為太陽赤緯,表達式為

τ=23.45°·sin[2π(nday+284)/365]

(11)

其中：ts為真太陽時間，其表達式為

ts=t±(Lo-Los)/15+es

(12)

其中：t為計算地點的標準時間(單位：h)；Lo為計算地點的經度；Los為計算地點所用的標準時間的位置的地理經度，“+”對應東半球，“-”表示西半球；es為真太陽時間和平均太陽時間之間的時差，其近似計算式為

es=0.164 5sin2B-0.125 5cosB-0.025sinB

(13)

式中：B=2π(nday-81)/365

(14)

至此得到了在某坐標、某海拔、某日期的太陽輻照日變化。

2.3 無人機六自由度運動模型

無人機的平移運動決定了其在大氣環境中的相對位置，角運動決定了光伏電池受光面與入射光的相對夾角，平移運動與角運動又共同影響了無人機所需推力和速度、即電機功率的大小。太陽能無人機的運動過程采用飛機六自由度運動模型描述，涉及12個狀態量，包括空速Vas、迎角α、側滑角β、滾轉角速度p、俯仰角速度q、偏航角速度r、滾轉角φ、俯仰角θ、偏航角ψ、向北位移xg、向東位移yg、飛行高度zg。

2.3.1 氣動系數

氣動系數的求解或者辨識是求取氣動力和力矩的前提，目前常用的求解方法是采用計算流體力學有限元軟件工具對無人機的幾何模型進行風動模擬實驗，將獲得的氣動數據結合氣動系數表達式進行插值運算來確定氣動系數中的各項參數[16]，氣動系數表達式如下：

1)滾轉力矩系數Cl

(15)

2)俯仰力矩系數Cm

(16)

3)偏航力矩系數Cn

(17)

4)升力系數CL

(18)

5)阻力系數CD

CD=CD0+CDaα

(19)

式中：CD0、CDα分別為零升阻力系數和迎角阻力導數。

6)側力系數CY

(20)

2.3.2 氣動力

假設無人機為剛體，飛行過程中不會產生形變和震動，則無人機所受的氣動力為

1)升力L

L=CLqdynSW

(21)

式中：SW為機翼參考面積；qdyn為飛行動壓，通過式(22)計算：

(22)

2)阻力D

D=CDqdynSW

(23)

3)側力Y

Y=CYqdynSW

(24)

2.3.3 氣動力矩

(25)

2)俯仰力矩M

M=CmqdynSWCbar

(26)

3)偏航力矩N

N=CnqdynSWbW

(27)

由式(22)可知，無人機的飛行動壓會隨著大氣密度而改變，繼而無人機所受的氣動力與力矩也會隨著海拔高低而不同。例如在低海拔下大氣密度大、空氣阻力大，無人機需要消耗更多的能量來穩定飛行速度，隨著海拔的升高、大氣密度降低、空氣阻力減少，無人機平飛所需功率降低，但是隨著海拔的繼續升高，空氣變得稀薄、升力將會降低，無人機又需要增加電機功率來保證飛行穩定，因此無人機的運動模型既要向前耦合承受大氣環境對氣動力和力矩的影響，同時也要向后耦合對能源系統的用電功率產生影響。

2.3.4 重力

飛機受到的力和力矩需要在機體坐標系下進行解算，利用坐標間的轉換關系可以得到重力矢量在機體坐標系下的表達形式為[17]：

(28)

式中：m為飛機的質量，下標g表示地面坐標系(原點位于飛機起飛點，Xg軸指向正北方，Yg軸指向正東方，Zg軸指向地心)，下標b表示機體坐標系(原點固定在飛機質心處，Xb軸位于無人機對稱平面內，并平行于無人機的縱軸且指向機頭，Yb軸垂直于無人機對稱平面，指向機身右方，Zb軸位于無人機對稱平面內，與Xb軸垂直并指向機身下方)。

2.3.5 推力

假設無人機由單螺旋槳提供推力，且螺旋槳的推力平行于Xb軸，所產生的推力為Tf，則機體坐標系下的推力為

(29)

2.3.6 飛機六自由度運動方程

在得到無人機受力與力矩之后，采用非線性微分方程組來描述飛機的六自由度運動，共12個方程，分別描述上述提到的12個狀態量。

1)受力方程組

(30)

2)角運動方程組

(31)

3)受力矩方程組

(32)

式中：Ix、Iy、Iz分別為無人機繞Xb軸、Yb軸、Zb軸的轉動慣量；Ixy、Ixz、Iyz分別為無人機相對于XbYb平面、XbZb平面、YbZb平面的慣性積。

4)導航方程組

(33)

式中：u、v、w分別為無人機在機體坐標系中沿著Xb、Yb、Zb軸的線速度分量，可通過式(34)求取

(34)

2.3.7 飛行控制器

六自由度運動模型是開環意義下的運動描述，還需要一套飛行控制器來穩定無人機的飛行，并將12個狀態量的控制過程轉變為無人機的操縱過程。參與無人機操縱的控制量包括：油門δT、升降舵角度δe、副翼角度δa、方向舵角度δr，上述控制量的調整會使無人機的氣動力和氣動力矩參數發生變化，從而改變無人機運動狀態[18]。由于飛機運動方程中的各個狀態量之間相互耦合，為了簡化飛行控制器的設計難度，通常要對飛機運動方程進行解耦。

當飛機處于水平無側滑飛行狀態時，有β≡0、φ≡0、p≡0、r≡0，基于該條件，可將無人機的飛行解耦為縱向和橫向2種運動的疊加，此時縱向運動狀態量為(Vas,α,q,θ,zg)，橫向運動狀態量為(β,φ,ψ,p,r)。無人機的運動被分成了縱向和橫向2個無耦合的運動形式，因此無人機的飛行控制可分為2個無耦合的縱向飛行控制器和橫向飛行控制器來設計。

1)縱向飛行控制器

參與縱向運動的控制變量是油門δT和升降舵角度δe，縱向控制器的控制過程即是對縱向運動的狀態量參考值進行跟蹤。縱向控制器框圖如圖4所示，其中GδT為油門的誤差放大增益列向量，Gδe為升降舵的誤差放大增益列向量。

圖4 縱向飛行控制器框圖

2)橫向飛行控制器

參與橫向運動的控制變量是副翼角度δa、方向舵角度δr，橫向控制器的控制過程即是對橫向運動的狀態量參考值進行跟蹤。橫向控制器框圖如圖5所示，其中Gδa為副翼的誤差放大增益列向量，Gδr為方向舵的誤差放大增益列向量。

圖5 橫向飛行控制器框圖

2.4 電機模型

太陽能無人機通常采用無刷直流電機作為動力裝置，無刷直流電機的數學模型為

(35)

式中：ra為電機內阻；Vmotor為電機兩端電壓；Imotor為通過電機的電流；Kv為電機KV值；Km為電機轉矩常數；nmotor為電機轉速；Mem為電機的電磁轉矩。

電機的輸出轉矩為

Mmotor=Mem-MR=Km(Imotor-I0)

(36)

式中：MR為克服空氣阻力的空載轉矩；I0為對應產生的空載電流。

電機的輸入功率為

Pmotor_in=VmotorImotor

(37)

電機的輸出功率為

Pmotor_out=2πnmotorMmotor/60

(38)

電機的效率為

ηmotor=2πnmotorMmotor/(60VmotorImotor)

(39)

2.5 減速組模型

太陽能無人機通常為輕型或超輕型飛機，飛行速度較慢，有時會使用減速組來降低螺旋槳的轉速，提高螺旋槳效率。假設減速組的減速比為K，機械效率為ηdecelerator，則有

(40)

式中：npropeller為螺旋槳轉速；Mpropeller為螺旋槳轉矩，式(40)表明減速器將原電機等效為一個KV值為原值的1/K的新電機。

2.6 螺旋槳模型

太陽能無人機的推力由螺旋槳產生，而螺旋槳的推力與大氣密度呈正相關關系，這導致能源系統中的動力負荷用電功率與外部大氣環境存在耦合。在描述螺旋槳時，首先有如下假設：

1)螺旋槳從電機吸收功率的過程中沒有產生損耗。

2)進程比J保持在一個較小的范圍內波動，這個范圍是最高效率點附近，此處假設J不變，J的典型值為0.65[19]，其定義為

J=Vas/(npropellerDp)

(41)

式中：Dp為螺旋槳直徑。

螺旋槳推力為

(42)

式中：CT為螺旋槳推力系數。

螺旋槳吸收功率為

(43)

式中：CP為螺旋槳功率系數。

CT和CP是與進程比J相關的數值，通常通過查找與J的關系曲線得到對應值，由于假設J不變，所以認為CT和CP也不變。

螺旋槳的輸出功率為

Ppropeller_out=TfVas

(44)

螺旋槳的效率為

(45)

2.7 光伏電池模型

光伏電池模型用來描述太陽能向電能的轉換過程，與地面使用的光伏電池不同，太陽能無人機的光伏電池模型不僅需要考慮自身的電壓-電流外特性，還要考慮無人機的姿態角度導致電池的受光面與入射光的夾角變化影響。

1)受光量與姿態角關系

式(8)給出的是太陽直射角度下的太陽輻照大小，但還需要考慮太陽入射光與受光平面的角度影響，即無人機的姿態角對光伏電池面板接受太陽輻照大小的定量影響。假設光伏電池平鋪在無人機機翼上，在式(8)基礎上加入太陽入射光與受光平面的夾角關系：

SPV=Ssinζ

(46)

cosφ=cos(π/2-ο)=sinο

(47)

太陽方位角μ可通過式(48)求取

cosμ=(sinοsinLa-sinτ)/(cosοcosLa)

(48)

圖6給出了太陽天頂角、高度角、方位角與太陽能無人機姿態角的示意圖。在地面坐標系XgYgZg中，向量s表示為

圖6 太陽能無人機的角度示意圖

s=[i1,i2,i3]=[-cosοcosμ,cosοsinμ,-sinο]

(49)

在機體坐標系XbYbZb中，v=[0, 0,-1]，由機體坐標系和地面坐標系的轉換關系，可得地面坐標系XgYgZg中的v表示為

(50)

(51)

所以考慮無人機姿態角的太陽輻照公式為

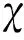
(52)

2)光伏電池外特性模型

太陽輻照和溫度對于光伏電池的外特性影響體現在短路參數、開路參數和最大功率點參數上，即短路電流Isc、開路電壓Ioc、最大功率點電流Im和最大功率點電壓Vm是受光照和溫度變化的函數，它們的計算式為

(53)

式中：Sref=1 000 W/m2，為參考太陽輻照值；Tref=25 ℃(298 K)為參考溫度；ΔS=SPV-Sref為實際光強與參考光強的差值；ΔT=T-Tref為實際溫度與參考溫度的差值；補償系數a=0.002 5/℃、b=0.000 5 W/m2、c=0.002 88/℃。

光伏電池的常用工程模型為

(54)

式中：VPV、IPV分別為光伏組件的端口電壓和電流，式(54)結合式(53)中的4個參數可以確定光伏電池的輸出外特性。

3)光伏電池不一致性

大翼展太陽能無人機的機翼表面有更多的可鋪設面積來布置更多的光伏電池，但光伏電池特性的不一致性影響也會隨著電池組合規模的增加變得更加明顯，最常見的問題是光伏組件輸出功率曲線由單峰特性變為多峰特性，因此對于大翼展太陽能無人機來說，光伏電池模型應進一步細化，通過將輸出電流方程(54)分段表示，可建立多峰特性的光伏電池模型[20]。此處假設有3組并聯的光伏組件分別為鋪設在機翼的左部、中部和右部，每組光伏電池均為特性不一致的單峰特性，組合輸出特性為多峰特性，則整個光伏陣列的輸出電流IPV_Σ為

(55)

式中：VPV_Σ為光伏陣列的電壓；Ileft和Voc_left為機翼左部光伏組件的輸出電流和開路電壓；Imid和Voc_mid為機翼中部光伏組件的輸出電流和開路電壓；Iright和Voc_right為機翼右部光伏組件的輸出電流和開路電壓，且有Voc_left

2.8 蓄電池模型

1)蓄電池外特性模型

蓄電池模型用來描述化學儲能和電能間的轉換過程，蓄電池模型采用內阻模型表示：

(56)

式中：VBAT為蓄電池電壓；IBAT為蓄電池電流；SOC為蓄電池的荷電狀態；SOC0為初始荷電狀態；V0為蓄電池開路電壓，根據當前荷電狀態SOC采用一維查表得到；r0為蓄電池內阻，根據當前荷電狀態SOC和蓄電池電流IBAT采用二維查表得到；CBAT為蓄電池容量。

2)蓄電池不一致性

大翼展太陽能無人機的蓄電池配置容量較大，通常由多個規格相同的獨立電池組組合成整個儲能系統，此時蓄電池的不一致性表現也會更加明顯，其中最直觀的表現就是電池串聯時組間電壓、內阻和容量的不一致，為此可用獨立模型建模方法[21]，對每個電池組采用式(56)分別進行建模，并考慮不同電池組間的特性參數差異，最后對電池組模型進行整合得到電池系統的特性模型，即對含有k個電池組的電池系統，有

(57)

式中：VBAT_Σ、V0_Σ、r0_Σ、SOCΣ分別為整個儲能系統的端口電壓、開路電壓、內阻和荷電狀態；VBAT_i、V0_i、r0_i、SOCi、SOC0_i、CBAT_i分別為第i個電池組的端口電壓、開路電壓、內阻、荷電狀態、初始荷電狀態和容量。

綜上，上述各個模型均與能源系統中的能量流動存在直接或間接關系，通過在各個模型間建立如圖3所示的參數關系，來建立大氣環境和飛行行為對能源系統運行的耦合作用，實現對太陽能無人機運動過程中的能量流動的完整計算與描述。對于準確性的追求使得模型的計算量較大，該耦合模型更適合用于仿真試驗，或是用作半實物平臺的仿真代碼模型。

3 模型仿真結果

根據上述模型描述，在SIMULINK中搭建太陽能無人機能源系統的仿真模型，無人機的外形尺寸、氣動系數、電池容量等參數參照文獻[22]設計的太陽能無人機MARAAL，該文同時提供了一組特定日期和地點的實際飛行數據，可作為本文模型仿真結果的有效對比，太陽能無人機的主要仿真參數如表1所示。

圖7為本文仿真結果與文獻[22]的實際飛行數據對比，可見在相同的飛行軌跡下仿真結果與實際數據基本保持一致，表明本文模型具備了可應用性。圖8為48 h內太陽能無人機飛行過程的仿真結果(為保證無人機的能量滿足過夜飛行，假設無人機上為高性能光伏電池與蓄電池，調整表1中光伏電池效率為29%，蓄電池能量比為260 W·h/kg)，于凌晨4點起飛，至第3天凌晨4點降落，整個過程包含了起飛、爬升、巡航、滑翔、降落等典型飛行狀態。

表1 太陽能無人機仿真參數

圖7 仿真結果與實際飛行數據對比

圖8 太陽能無人機飛行仿真結果

圖9為飛行過程中太陽輻照的變化情況，包含太陽輻照直射值(即計算平面與太陽光線垂直時的太陽輻照大小)、地表平面太陽輻照值(即計算平面與地表平行時的太陽輻照大小)、無人機上光伏電池表面的太陽輻照值。可見由于無人機的姿態角度關系，使得布置在機翼上的光伏電池受光程度與地表平面相比出現了差異。例如，在中午12點后的t4～t5時段，此時太陽光線轉為從西面射入地表，而由圖8(d)可見，該時段中無人機向東北飛行、仰角大于0，所以此時光伏電池表面法線和太陽光線的夾角小于地表平面法線和太陽光線的夾角，使得電池受光量比地表平面要大；而在t5～t6時段，無人機轉向西南飛行，此時光伏電池表面法線和太陽光線的夾角大于地表平面法線和太陽光線的夾角，使得電池受光量與地表平面相比要小。以上體現了姿態角度對獲取太陽能大小的耦合影響。

圖9 48小時內的太陽輻照變化

圖10和圖11為飛行過程中能源系統的功率流動和蓄電池電量變化情況。在起飛至t1時刻，此時沒有光照，只有蓄電池向負載供電；t1時刻后日出，此時光伏電池與蓄電池同時向負載供電；t2時刻，光伏電池發出功率滿足負載用電、并向蓄電池充電；至t3時刻完成爬升開始平飛，用電功率下降；t4時刻蓄電池的電量充滿，此時無人機再爬升，用電功率增加，將多余的電能轉換為重力勢能，并且為了穩定能源系統負載母線電壓，能量管理器中的光伏電池控制環不再工作在最大功率點跟蹤方式，而是工作在負載功率點跟蹤方式，降低光伏電池輸出功率以保證母線穩定；t5時刻完成爬升并平飛，由于飛行高度升高，大氣密度降低、空氣阻力減小，所以此時的螺旋槳推力、平飛功率與t3～t4時段相比略有減小；t6時刻光照下降至光伏電池出力不再滿足負載所需，蓄電池開始供電；t7時刻，太陽輻照為零，轉由蓄電池獨立供電，此時優先消耗重力勢能，無人機進行滑翔、降低負載功率，達到夜間平飛高度后開始夜間巡航，蓄電池電量被不斷消耗；第2天t8時刻后光照上升，光伏電池和蓄電池聯合供電，完成了一日的能量閉環飛行；t9時刻，光伏電池向蓄電池充電；t10～t11時刻無人機爬升到日間平飛高度，由于蓄電池電量未滿，光伏電池一直工作在最大功率點；直至t12時刻光伏電池輸出功率不足，蓄電池開始放電，蓄電池電量不斷減少；t13時刻無人機滑翔至夜間飛行高度，消耗重力勢能；t14時刻蓄電池電量不足，無人機降落。以上過程體現了無人機能源系統中電能的直接變化以及太陽能、化學儲能和重力勢能的間接變化過程。

圖10 48小時內的能源系統功率流動過程

圖11 48小時內的蓄電池電量(SOC)變化

4 基于耦合模型的半實物仿真平臺

圖12給出了基于能源系統多維耦合模型搭建的半實物仿真平臺的設計架構，其中大氣環境、無人機的運動、光伏電池、動力負荷(螺旋槳、減速器、電機)等相關數據通過計算機實時解算模型得到；蓄電池和能量管理器為真實實物；光伏電池的實物用可編程光伏模擬器代替，模擬器經通信接收計算機仿真得到的光伏電池外特性參數、實時的調節模擬器的光伏曲線，來模擬無人機機翼上光伏電池的輸出特性；電機負載的實物通過可編程電子負載代替，與光伏電池類似，電子負載經通信接收計算機仿真得到的負載功率參數、實時的調節電子負載的阻值，來模擬無人機上動力負荷的用電過程。

圖12 半實物仿真平臺設計架構

圖13為實驗室內搭建的基于多維耦合模型的半實物仿真平臺樣機，其中能量管理器的電路拓撲采用三端口直流變換器[23]，可通過單級電路同時對光伏電池、蓄電池和負載母線進行功率控制；使用MATLAB腳本編寫能源系統模型代碼，使用Labview開發可視化界面，將模型腳本嵌入至Labview中實時運行，可視化界面如圖14所至Labview中實時運行，可視化界面如圖14所示。計算機作為上位實時系統，其后端負責實時計算獲取模型數據，并接收能量管理器的決策指令；前端負責顯示太陽能無人機的位置、姿態、航跡信息和三維模擬動畫，同時接收能量管理器的上傳數據，將實際的光伏電池、蓄電池和負載的電壓、電流、電量和功率流向顯示出來。

圖13 半實物仿真平臺樣機

圖14 半實物仿真軟件界面

基于耦合模型搭建的半實物仿真平臺，為太陽能無人機的能量管理器提供了一個低成本的驗證途徑，即不必搭建完整的飛機實物、不必進行代價高昂的飛行試驗，便可以在地面、實驗室內對能量管理器的電路拓撲和能量管理策略進行有效的實機驗證。該平臺與全計算機仿真相比實驗結果更為真實，與真實飛行試驗相比更為安全、高效，適合作為過渡平臺使用，滿足了在太陽能無人機能源系統的理論設計轉向工程研發過程中的驗證工作需求，尤其是加快太陽能無人機能量管理器的電路設計和能量管理算法的開發效率。關于半實物仿真平臺的詳細設計將另文闡述，本文不再說明。

5 結 論

1)在建模過程中耦合外部大氣環境和無人機飛行姿態對太陽能無人機能源系統運行的影響，解算在任意日期、時間、地點、高度、飛行姿態下的太陽能無人機能源系統發電與用電數據，結果更加準確、模型更加完善，適合用于計算機仿真解算特定參數變化對無人機能源系統運行的影響。

2)仿真結果驗證了無人機能源系統產能與耗能過程中外部大氣環境和飛行姿態對能量流動產生的影響，尤其是大氣環境和飛行姿態對光伏電池功率和動力負荷功率的影響。

3)給出了基于耦合模型的太陽能無人機半實物仿真平臺搭建方案，計算機負責實時仿真大氣環境和無人機運動過程，經實時通信調節光伏模擬器與電子負載的運行參數，來模擬無人機上光伏電池的發電和動力負荷的用電過程，能量管理器作為被驗證的實物參與運行。該平臺可作為太陽能無人機的地面實驗平臺使用，有助于加快無人機能量管理器的開發與驗證工作。