等離子體合成射流對鈍頭激波的控制與減阻
陳加政,胡國暾,樊國超,陳偉芳,*
1.浙江大學 航空航天學院,杭州 310027 2.中國運載火箭技術研究院 研究發(fā)展中心,北京 100076
等離子體合成射流作為一種主動流動控制方法[1],由于其激勵器具有體積小、響應快和射流速度高等工作特點,可在不改變飛行器整體外形的情況下對其流場進行流動控制,從而改善飛行器的氣動特性和可操控性,為飛行器的設計和優(yōu)化提供冗余空間。其近年來在邊界層控制[2-4]和高速流動控制領域[5-7]逐漸展現了良好的工程應用前景。
為了探究等離子體合成射流對流場的作用機理和控制效果,國內外大量學者對其進行了數值模擬研究。Grossman等[8]發(fā)展了一個瞬時加熱模型,其認為激勵器腔體內能量沉積過程瞬間完成,將激勵器腔內氣體設定較高初始溫度和壓力,對激勵器腔體及其出口流場進行了數值模擬。Cybyk等[9-10]也采取了類似的思路,研究了激勵器出口直徑、腔體大小及能量沉積大小對“SparkJet”激勵器性能的影響。國內的張宇[11]也利用了該方法,研究了兩電極等離子體合成射流激勵器的直接力工作特性。劉朋沖等[12]則根據分子平轉動迅速平衡的特點,直接利用激勵器內放電等離子體的轉動溫度為800 K的光譜結果,將其設為仿真的溫度邊界條件,通過控制持續(xù)時間來調整能量注入大小,研究了單次放電激勵器流場的演化規(guī)律以及不同放電時間尺度對激勵器出口速度的影響。
由于Grossman的瞬時加熱模型不能描述能量沉積過程,仿真的初始條件嚴重依賴于簡化的理論分析模型的精確性,難以真實反映激勵器的射流速度、流場結構、工作周期等特性,因此學界又進一步發(fā)展了相應的能量源項模型。單勇等[13]認為,能量沉積的平均效果可以通過在一定時間內注入不變的能量來表示,從而能在能量控制方程中添加源項來模擬放電后在腔體內產生的高能量密度環(huán)境,并在考慮固體外壁面與外界環(huán)境的輻射換熱的條件下,數值模擬了等離子體合成射流激勵器的流場,獲得了流場的典型結構。Lv等[14]則在此基礎上,進一步研究了激勵器頻率、壁面換熱系數以及壁面溫度對激勵器性能的影響。顧仁勇等[15]也利用該方法對運輸機后體流動分離進行了主動控制的數值研究。與此同時,國防科技大學的羅振兵團隊[16-18]也通過能量源項模型研究了等離子體合成射流的一些特性。他們在腔體內能量注入的基礎上,還考慮了等離子體氣體的部分熱力學特性。
在能量源項模型的基礎上,本文進一步完善了等離子體在熱完全氣體效應下的熱力學屬性和輸運參數,從而提高了數值模擬中激勵器放電功率的上限與計算的穩(wěn)定性,改善了能量源項模型的計算精度與適用范圍。同時,通過對超聲速平板流場的動態(tài)模擬,對比分析不同熱力學參數下合成射流對主流的干擾作用以及流場結構的演化過程,探究等離子體合成射流對邊界層流動發(fā)展的作用效果,同時驗證等離子體物性參數擬合的必要性。通過對馬赫數為3超聲速球頭流場的動態(tài)模擬,探究等離子體合成射流對球頭流場的調控作用,并分析其對球頭激波及其阻力的影響規(guī)律,為鈍頭體飛行器的減阻布局設計提供數值依據。
1 等離子體合成射流數值建模
1.1 能量源項模型
針對等離子體合成射流,考慮其物理機制主要為氣體放電的電加熱作用,因此可以將激勵下復雜的物理化學流動簡化為唯象的能量源項模型,把放電的能量沉積添加到控制方程的源項中,從而模擬等離子體射流的形成。其數值控制方程為
(1)

剪切應力τij的表達式為
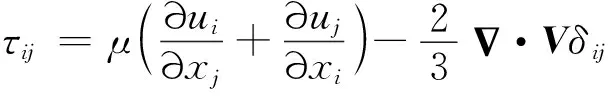
(2)
式中:μ為動力黏性系數;V為速度矢量;δij為應力張量分量。

(3)
(4)
式中:Ein為激勵器消耗總能量大小;ηe為能量轉化效率;t為時間;n為周期數;T為周期時間;V為放電區(qū)域體積;τ為每個周期內輸入能量的持續(xù)時間;Qav為放電總能量轉化成氣體熱能的能量密度,W/m3。
1.2 等離子體的熱力學屬性與輸運系數
當等離子體合成射流激勵器發(fā)生放電作用后,腔體內的溫度將迅速上升,空氣發(fā)生電離形成具有較高溫度的等離子體。此時,腔內氣體將不再是量熱完全氣體,其熱力學性質將發(fā)生改變。因此,為求解式(1),必須先給定定壓比熱cp、熱傳導系數κ與黏性系數μ等參數,其隨溫度和壓力的變化而變化。但腔體內等離子體成分方程復雜,而射流的非定常特性又使得直接采用化學非平衡動力學方程求解異常低效。因此本文將等離子體視為熱完全氣體(單一組分),采用工程擬合公式來計算等離子體的物性參數,從而快速地求解等離子體控制方程式(1),同時滿足激勵器不同放電功率下的計算精度要求。而對于等離子體物性參數的工程擬合公式,本文選取Capitelli[19]與Gupta[20]等的研究成果,其溫度范圍在50~30 000 K 左右,具體參數可參考文獻[19-20]。
等離子體的定壓比熱為
cp=exp(aζ4+bζ3+cζ2+dζ+e)
(5)
等離子體的黏性系數為
(6)
等離子體的熱傳導系數為
(7)
式中:
ζ=ln(T/10 000)
(8)
(9)
γ(T,b,c)=e-[(T-b)/c]2
(10)
式(5)~式(7)中唯一自變量為熱力學溫度T,其他參數均為擬合參數。當溫度小于 30 000 K 時,定壓比熱cp、焓值h、黏性系數μ和熱傳導系數κ隨溫度變化的曲線如圖1所示。其中,cp_Constant表示定壓比熱為常數1 006.43 J/(kg·K),適用于量熱完全氣體;cp_Gupta91適用于處于局部熱力學平衡態(tài)的空氣,為式(5)的擬合結果。h_Linear和h_Gupta91分別表示cp為常數和擬合積分結果對應的焓值。μ_Sutherland表示采用Sutherland公式計算的黏性系數;μ_Capitelli 表示式(6)擬合結果。κ_Sutherland表示黏性采用Sutherland公式計算對應的熱傳導系數;κ_Capitelli為式(7)的擬合結果;κ_Experiment為實驗結果[19]。

圖1 定壓比熱、焓值、黏性系數和熱傳導系數隨溫度的變化曲線
由圖1可見,在2 000 K以下等離子體氣體的定壓比熱、黏性系數和熱傳導系數與完全氣體相差不大。但2 000 K之后隨著溫度的逐漸升高,等離子體氣體的熱力學屬性與輸運系數相比量熱完全氣體的誤差逐漸增大,甚至達到1~2個數量級的差異。而激勵器中在劇烈放電作用下溫度可達約10 000 K,將其當作量熱完全氣體處理存在較大的誤差。
2 合成射流流動控制
2.1 超聲速平板邊界層控制
算例采用三維結構網格數值仿真,對稱面計算網格如圖2所示,左端壓力入口距噴口130 mm,右端壓力出口距噴口100 mm,上端壓力遠場距噴口100 mm,展向寬度為100 mm。外部流場網格數目為221×101×101,總網格量(含激勵器)為320萬。噴管直徑為3 mm,長5.5 mm,激勵器為直徑7.5 mm、高10 mm的圓柱體,放電區(qū)域為腔體中間1/4區(qū)域,放電時間為20 μs,注入能量為1.92 J。來流條件與文獻[16]中實驗一致,靜溫為166.7 K,靜壓為12 950 Pa,馬赫數為2。壁溫取來流靜溫。計算時間步長為1×10-8s,內迭代步數為20。湍流模型采用RNGk-ε模型[21]。
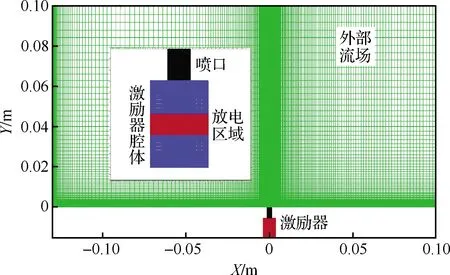
圖2 平板流場計算域及其網格
圖3展示了激勵器放電能量效率為10%時采用式(5)~式(7)計算的結果。為了方便與文獻[16]的實驗紋影圖結果進行對比,采用密度梯度灰度圖顯示,其中A系列代表計算結果,B系列代表實驗紋影圖,H為等離子體合成射流誘導的弓形激波最大高度。由圖可見,對于超聲速平板流場的基本結構,數值模擬結果在流場大尺度結構上與實驗較為符合,但在時間上存在約10 μs的滯后。這主要是由于計算中能量是在放電階段均勻注入,而真實激勵器工作電壓在放電前半階段較大并逐漸變小,大部分能量在前半段注入,從而造成了約為放電時間一半即10 μs的時滯。對于數值模擬結果,在35 μs左右,已可以觀察到明顯的由合成射流引起的弓形激波,并開始向下游發(fā)展。約從60 μs開始,大尺度渦開始形成,并由于主流作用向下游傳播。150 μs左右,擴大的弓形激波轉變?yōu)樾奔げǎ⒃?00 μs時強度達到最大。此后斜激波逐漸減弱,且渦結構也逐漸耗散消失。

圖3 合成射流作用下平板流場結構演化實驗[16]與數值模擬結果比較
為了更好地分析能量效率和定壓比熱的選取對合成射流計算結果的影響,圖4給出了不同能量效率下等離子體合成射流誘導的弓形激波最大高度H隨時間的變化。
圖4中百分數表示能量效率,虛線表示定壓比熱采用常數形式,取值為1 006.43 J/(kg·K),而實線表示定壓比熱采用擬合公式的計算結果,Exp為文獻[16]中的實驗數據。由圖4可見,對于常數定壓比熱的情況,其弓形激波最大高度的時間演化規(guī)律較為一致,能量效率越高,其值越大,曲線的斜率也有所上升,5%能量效率的結果與實驗吻合較好,但曲線斜率相較實驗結果更大。而采用擬合公式定壓比熱的結果,10%能量效率的結果與實驗吻合很好,盡管能量效率選取較大,但弓形激波最大高度卻上升不多,其斜率小于常數定壓比熱的曲線。這是因為擬合公式獲得的定壓比熱在等離子體溫度上升到較高值時比常數值要大得多,氣體的焓值高,吸熱能力上升了。對于相同的能量密度,擬合公式的結果使氣體內能增加而動能減少,流場結構的發(fā)展更加緩慢,表現為弓形激波高度和增長斜率都會減小,從而得到與實驗更為符合的結果。

圖4 弓形激波最大高度時間演化曲線
2.2 鈍頭激波控制與減阻
算例采用軸對稱仿真,其計算區(qū)域如圖5所示,壁面網格加密,總網格量為26萬。來流靜溫107.1 K,靜壓2 758 Pa,馬赫數為3,單位雷諾數為7.5×106。鈍頭、腔體和噴管壁設為無滑移等溫壁,壁溫取來流靜溫。鈍頭直徑50 mm,噴管直徑9 mm,長4.5 mm,激勵器為直徑12.4 mm、高12.4 mm的圓柱體,放電區(qū)域依舊為腔體中間1/4區(qū)域,放電時間為15 μs。穩(wěn)態(tài)條件下(射流未啟動)數值模擬結果顯示激波脫體距離為5.5 mm,總阻力(包括壓差阻力和黏性阻力)大小為35.0 N。

圖5 球頭流場計算域及其網格
圖6給出了實際注入熱能Qin=Ein·ηe=270 mJ的合成射流作用下流場結構密度梯度灰度圖。由圖6可知,在24 μs左右,射流開始在鈍頭頭部出現。40 μs時刻在激勵作用下,頭部激波的頂端被推向上游并形成一個凸起。60 μs和80 μs,頭部激波進一步被推向上游,高溫低密度射流在頭部激波和鈍頭體之間擴散,并有部分開始沿鈍頭體表面向下游流動。在100 μs左右,射流的強度達到峰值,頭部激波的前移距離達到最大。此時由于射流的速度較大,密度較低,為了平衡球頭弓形激波后的低速高密度特性,在射流內部產生了一道正激波。之后,射流變得越來越弱,空氣開始重新填充激勵器腔體。在280 μs左右,射流基本噴射完成,將開始下一個周期的運動。
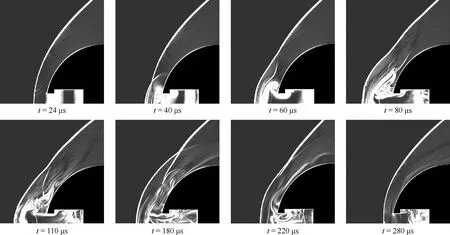
圖6 合成射流作用下球頭流場結構隨時間的演化
圖7給出了在前2個周期內,鈍頭流場弓形激波的脫體距離隨時間演化的情況。其中Steady表示無射流定常狀態(tài)下的激波脫體距離,Transient表示激勵器工作時的結果。由圖可見激波脫體距離隨時間呈明顯周期性變化。對于第1個周期,激波脫體距離在125 μs時達到最大,為14.86 mm;而在290 μs達到最小,為3.77 mm。相較于未施加射流時5.5 mm的情況,激波脫體距離最大增加了2倍,由此可見在射流周期的噴階段,等離子體合成射流對頭部激波有較強的控制作用。
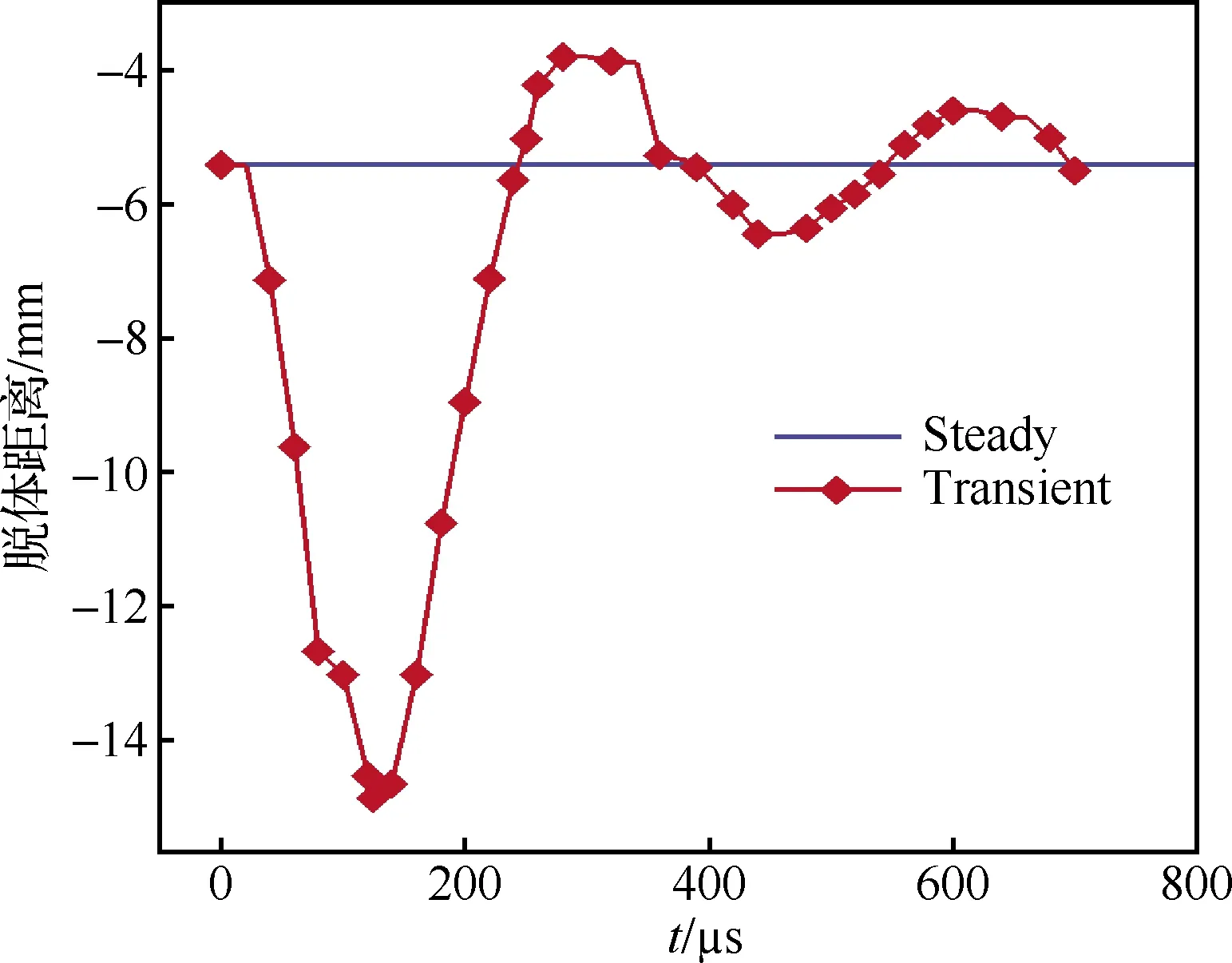
圖7 激波脫體距離隨時間的變化
由圖8可知,等離子體合成射流的噴口(Exit)平均速度(V)和鈍頭阻力(D)同樣呈明顯的周期性變化,且阻力變化相較速度有遲滯現象。在主射流結束后,激勵器會出現二次射流,但其強度較主射流有大幅下降,阻力和射流速度變化幅度都明顯減小。在第1個周期內即主射流作用下,相較于無射流定常狀態(tài),平均阻力降低了6.3%,而阻力最大則降低了32.0%。可見合成射流有較強的減阻效應。
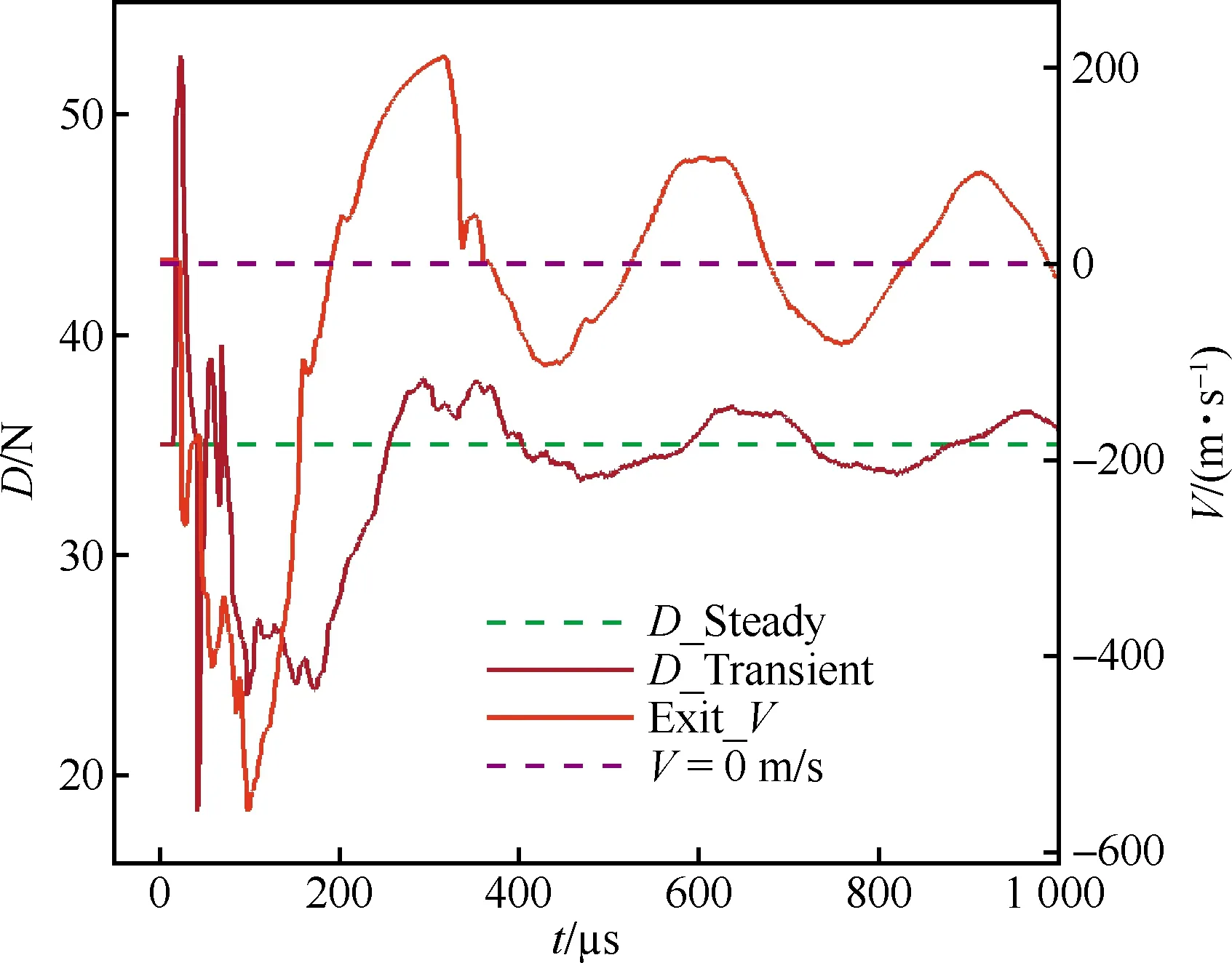
圖8 噴口平均速度與阻力隨時間的變化
為了更好地解釋球頭阻力特性的演化規(guī)律,圖9給出了0~42 μs激勵器腔體的壓力變化云圖。由圖9可知,對于圖8中阻力演化初期階段的2個跳躍,是由激勵器內氣體運動造成的。在阻力的極大值處,由10~20 μs的壓力云圖可見,等離子體放電產生的高溫高壓區(qū)形成正激波向兩側傳播,傳播到激勵器兩端使激勵器壁面壓力驟然上升,而左側肩部壁面面積較底部小,使得合力為阻力,從而使阻力有劇烈上升但持續(xù)時間很短;在極小值處,由20~42 μs的壓力云圖可見,在噴口的拐角處由于膨脹而產生了2個低壓區(qū),同時入口肩部氣流由于低壓抽吸以及噴射作用下的氣體流失也產生了低壓區(qū),并與出口處相持。但與此同時激波在底部反射離開而使底部壓力下降,阻力減小。之后反射波到達肩部使其壓力迅速上升,從而使阻力急劇減小。50 μs后激勵器內部激波消散,阻力變化主要由激勵器外部射流和主流作用引起。
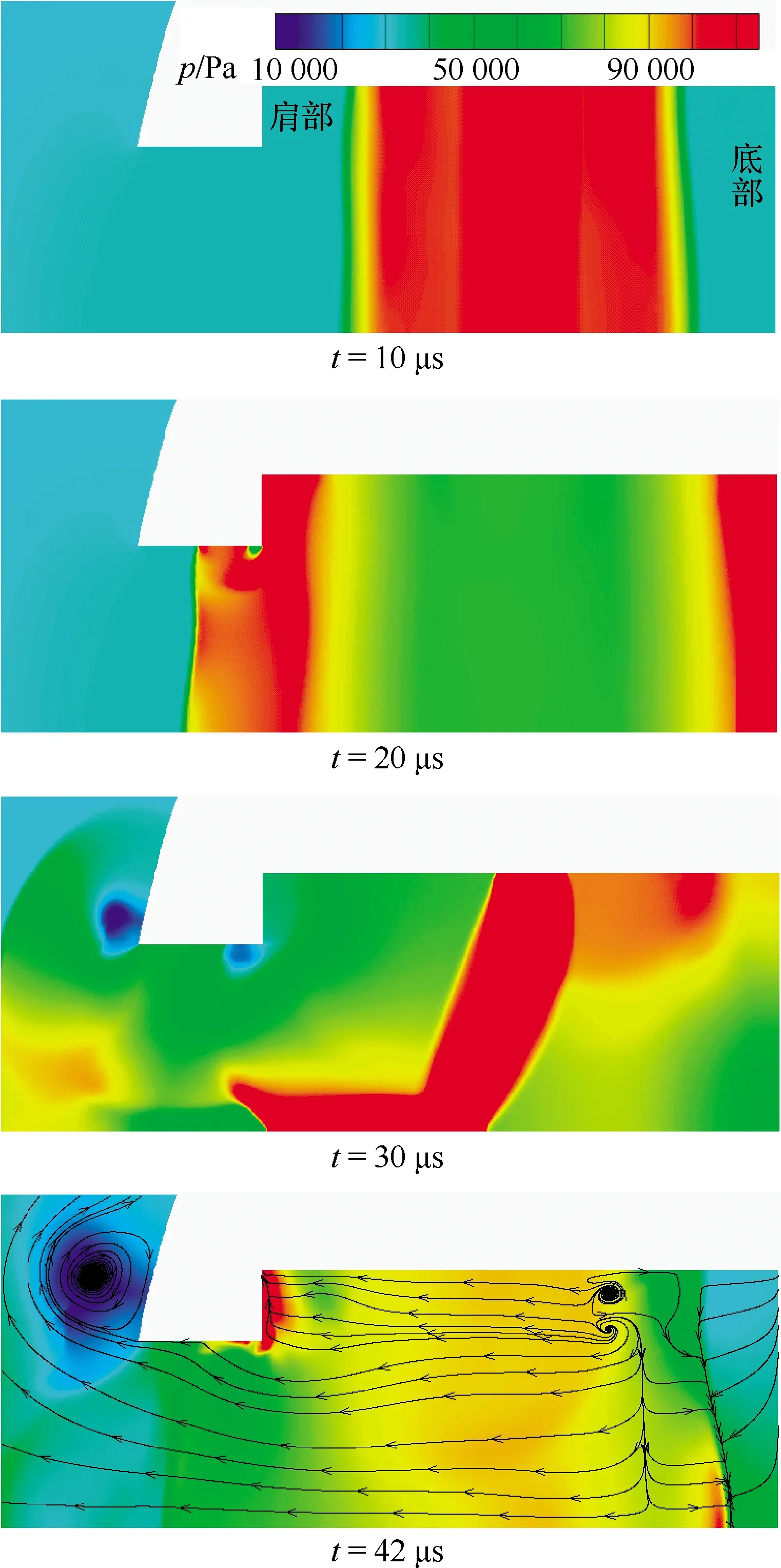
圖9 射流早期激勵器腔體與出口壓力云圖
圖10則說明了阻力在射流各階段變化的原因。對于射流的演化而言,其噴階段弓形激波外推,波后的壓力總體降低約10 kPa,并且射流形成了渦對低壓區(qū),2種共同作用使阻力減少。而吸階段激波脫體距離逐漸減小,波后壓力隨之升高,腔體內形成高壓區(qū),從而使阻力增大,且阻力相比速度周期具有滯后性。滯后性則是因為在剛開始的轉換階段,比如噴轉吸,低壓區(qū)不會馬上消失,而是慢慢減小,故阻力不會立刻轉換。
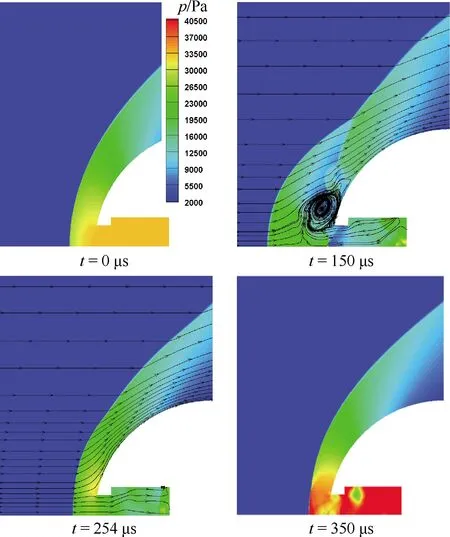
圖10 典型時刻流場壓力云圖
圖11說明盡管能量會被耗散或傳遞至下游,但還是有相當一部分高溫高壓氣體被二次吸入致使腔體增壓,在腔體內形成高壓區(qū),進而產生強度較小的二次射流,又使脫體距離增加,形成周期性振蕩。

圖11 典型時刻流場焓值云圖
為使計算結果更具普遍性和參考,下面給出了實際放電氣體熱能Qin注入為108、162、216、270、324 mJ的數值模擬結果對比。由圖12、圖13 可以看出,整體上不同熱能注入的計算結果阻力和射流速度變化規(guī)律基本相同,分為噴階段和吸階段。熱能的大小主要影響噴階段,隨熱能的增大,射流速度的最大速度和能量增大導致激波外推距離變大,波后壓力減小使減阻效應更顯著。而吸階段阻力和回填速度變化不大,其與注入熱能的大小幾乎無關。并且噴吸各階段持續(xù)時間不隨熱能大小變化而變化,整個作用周期為固定值。

圖12 不同熱能下出口速度變化
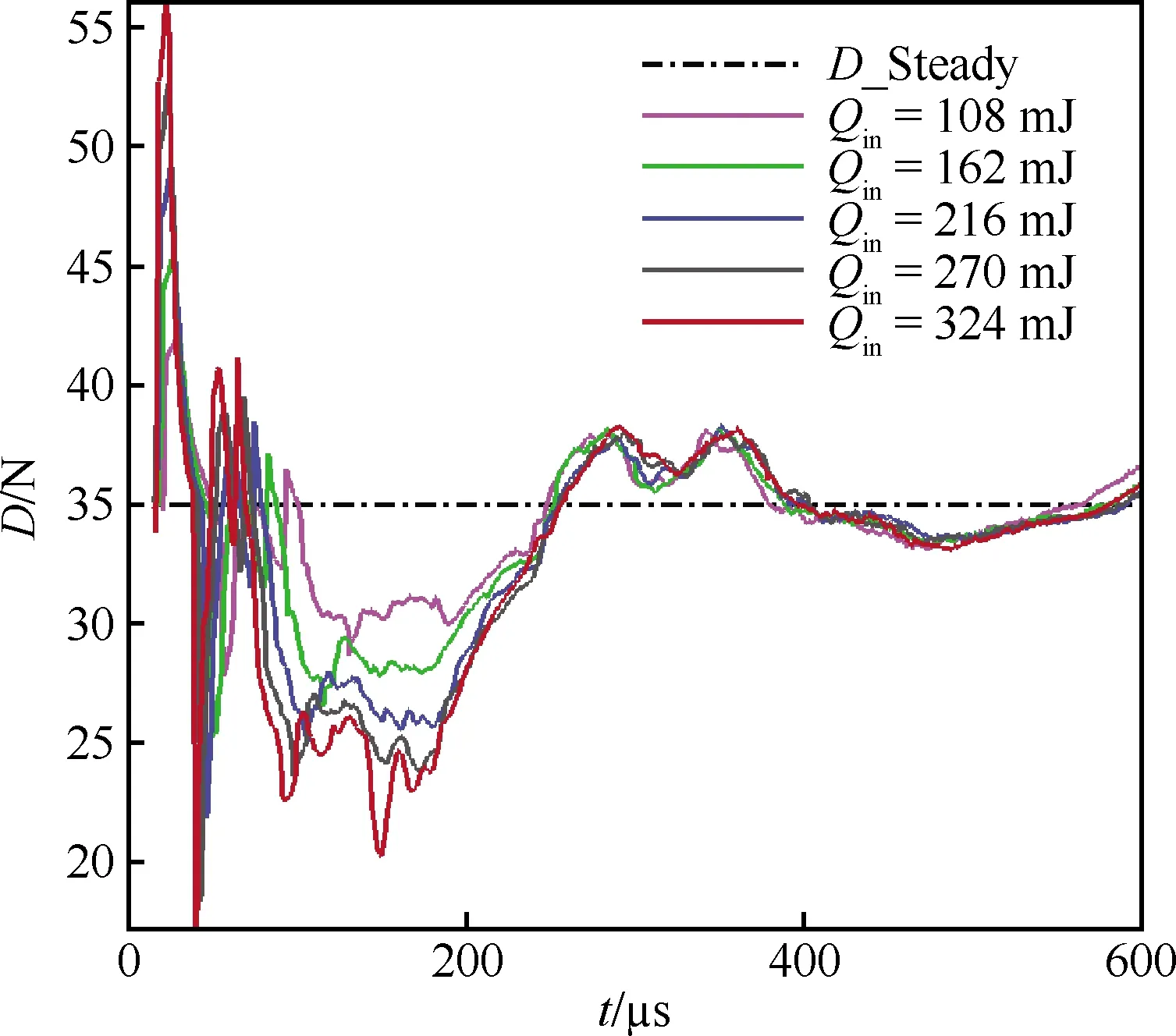
圖13 不同熱能下阻力變化
等離子體合成射流控制鈍頭激波的最終目的是減小鈍頭飛行器的能量消耗,減阻所節(jié)約的能量需大于激勵器所消耗的能量。
激勵器消耗的總能量為

(11)
式中:Ein為電容能量;Cd為電容大小;Vb為擊穿電壓。擊穿電壓需實驗測量,其與兩極距離、介質等有關。
激勵器所消耗的總能量存在電路的耗散和其他的能量損失,因此放電實際注入熱能為

(12)
式中:Td為放電時間;U(t)為瞬態(tài)電壓;I(t)為瞬態(tài)電流。
一個放電周期減阻收益的能量為

(13)
式中:D0為定常狀態(tài)阻力;D(t)為瞬態(tài)阻力;U∞為自由來流速度。表1給出了不同能量注入的減阻收益對比,表中ηb為減阻收益大于消耗總能量的最小能量效率。
由表1可以看出,減小的阻力所節(jié)約的能量是遠大于放電實際注入的熱能。但由于放電電路的耗散和其他的能量損失,激勵器消耗的總能量不能全部轉化為所注入的熱能。鈍頭激勵器由于弓形激波的壓縮作用,其激勵器腔體內壓力為33 kPa,較高的環(huán)境壓強能明顯提升激勵器的工作性能[22]。并且文獻[16, 23]中提出的三電極激勵器,其通過對電極間隙、電容、電壓等激勵器參數選取優(yōu)化,放電效率最高可達80%以上,即能實現減小整個系統(tǒng)能量消耗的目的。

表1 減阻收益對比
由于等離子體合成射流單次放電的控制作用時間短,在工程應用中一般以一定頻率多次脈沖放電的形式為主。而等離子體激勵器單個工作周期為能量沉積、射流噴出和吸氣復原3個階段,下個放電時刻應在激勵器吸氣復原之后且避開二次射流射出階段,否則激勵器工作效果不佳。本文選取復原剛好完成時刻進行下次放電,周期為365 μs,該放電頻率為飽和頻率2 740 Hz。由圖14 可以看出,各周期的射流速度和阻力變化規(guī)律與單周期基本相同,第1個周期與后續(xù)周期略有不同,后續(xù)周期射流峰值較大。圖示4個放電周期的阻力平均值相比定常減小6.1%,與單周期6.3%相差不大。這說明當放電頻率小于飽和頻率,多放電周期可以看作單周期的疊加。
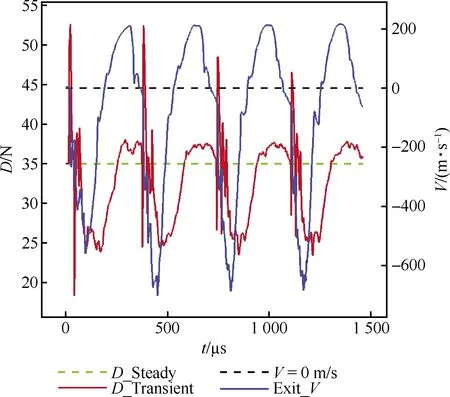
圖14 多周期噴口平均速度與阻力變化
3 結 論
本文考慮放電作用下熱完全氣體效應,進一步完善了能量源項模型,并對超聲速條件下平板邊界層和鈍頭流場合成射流流動控制進行數值模擬,主要有以下結論:
1)激勵器放電后等離子體射流的溫度很高,其物性與量熱完全氣體有較大差異。在平板邊界層控制模擬中,物性參數的工程擬合顯著提高了計算的準確性,流場結構與實驗吻合較好。
2)鈍頭流場減阻機理為:在射流噴階段,弓形激波外推使波后壓力減小,且噴口形成渦對低壓區(qū),兩者共同作用使阻力減小;而在射流吸階段,射流形成的渦對低壓區(qū)消失,且弓形激波脫體距離減小使波后壓力增大,使阻力增大。
3)注入熱能的大小主要影響噴階段,射流速度和減阻效果隨熱能的增大而增大。吸階段和激勵器工作周期基本不受熱能大小變化影響。
4)對于激勵器單次放電,主射流結束后,腔體內形成高壓區(qū),進而產生強度較小的二次射流,使脫體距離增加,形成周期性振蕩。激波脫體距離、噴口速度和球頭阻力都呈現明顯的周期性變化。對于多次脈沖放電,若放電頻率小于飽和頻率,各放電周期控制效果與單次放電周期基本相同。

